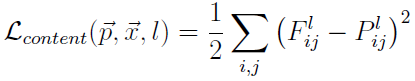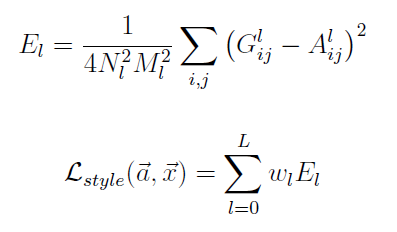Neural Art

發表於 | 分類於 | [object Object]

Art with Neural Network


風格, 創作這種能力在現在Alpha Go已經稱霸的時代, 目前覺得還是人類獨有的
不過有趣的是, 對於那些已經在 ImageNet 訓練得非常好的模型, 如: VGG-19, 我們通常已經同意模型可以辨別一些較抽象的概念
那麼是否模型裡, 也有具備類似風格和創作的元素呢? 又或者風格在模型裡該怎麼表達?

本篇文章主要是介紹這篇 A Neural Algorithm of Artistic Style 的概念和實作, 另外一個很好的投影片 by Mark Chang 也很值得參考

先給出範例結果, 結果 = 原始的內容 + 希望的風格

  • Content Image
  • Style Image
  • Result Image

說在前頭的最佳化

在講下去之前, 我們先講 NN 的事情, 一般情況, 我們是給定 input image x, 而參數 w 則是要求的變數, 同時對 loss (objective function) 做 optimize, 實作上就是 backprob.
上面講到的三種東西列出來:

  1. x: input image (given, constant)
  2. w: NN parameters (variables)
  3. loss: objective function which is correlated to some desired measure

事實上, backprob 的計算 x and w 角色可以互換. 也就是將 w 固定為 constant, 而 x 變成 variables, 如此一來, 我們一樣可以用 backprob 去計算出最佳的 image x.
因此, 如果我們能將 loss 定義得與風格和內容高度相關, 那麼求得的最佳 image x 就會有原始的內容和希望的風格了!
那麼再來就很明確了, 我們要定義出什麼是 Content Loss 和 Style Loss 了

Content Loss

針對一個已經訓練好的 model, 我們常常將它拿來做 feature extraction. 例如一個 DNN 把它最後一層辨識的 softmax 層拿掉, 而它的前一層的 response (做forward的結果), 就會是對於原始 input 的一種 encoding. 理論上也會有很好的鑑別力 (因最只差最後一層的softmax).

Udacity 的 traffic-sign detection 也有拿 VGG-19, ResNet, 和 gooLeNet 做 feature extraction, 然後只訓練重新加上的 softmax layer 來得到很高的辨識率.

因此, 我們可以將 forward 的 response image 當作是一種 measure content 的指標!
知道這個理由後, 原文公式就很好理解, 引用如下:

So let p and x be the original image and the image that is generated and Pl and Fl their respective feature representation in layer l. We then define the squared-error loss between the two feature representations

簡單來說 Pl 是 content image P 在 l 層的 response, 而 Fl 是 input image x (記得嗎? 它是變數喔) 在 l 層的 response.
這兩個 responses 的 squared-error 定義為 content loss, 要愈小愈好. 由於 response 為 input 的某種 encoded feature, 所以它們如果愈接近, input 就會愈接近了 (content就愈接近).
引用 Mark Chang 的投影片: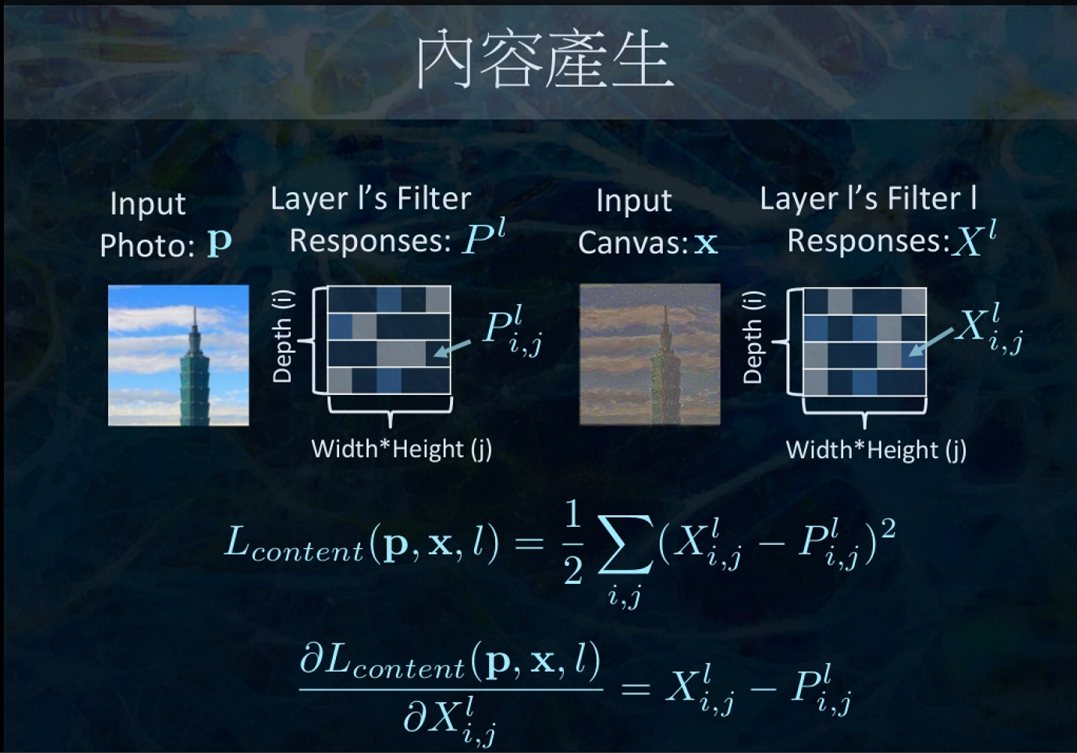

Style Loss

個人覺得最神奇的地方就在這裡了! 當時自己怎麼猜測都沒猜到可以這麼 formulate.
我個人的理解是基於 CNN 來解釋
假設對於某一層 ConvNet 的 kernel 為 w*h*k (width, hieght, depth), ConvNet 的 k 通常代表了有幾種 feature maps
說白一點, 有 k 種 filter responses 的結果, 例如第一種是線條類的response, 第二種是弧形類的responses … 等等
而風格就是這些 responses 的 correlation matrix! (實際上用 Gram matrix, 但意義類似)
基於我們對於 CNN 的理解, 愈後面的 layers 能處理愈抽象的概念, 因此愈後面的 Gram matrix 也就愈能代表抽象的 style 概念.
原文公式引用如下:

總之就是計算在 l 層上, sytle image a 和 input image x 它們的 Gram matrix 的 L2-norm 值

一樣再一次引用 Mark Chang 的投影片:

也可以去看看他的投影片, 有不同角度的解釋

實戰

主要參考此 gitHub
一開始 load VGG-19 model 就不說了, 主要的兩個 loss, codes 如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def content_loss_func(sess, model):
    """
    Content loss function as defined in the paper.
    """
    def _content_loss(p, x):
        # N is the number of filters (at layer l).
        N = p.shape[3]
        # M is the height times the width of the feature map (at layer l).
        M = p.shape[1] * p.shape[2]
        # Interestingly, the paper uses this form instead:
        #
        #   0.5 * tf.reduce_sum(tf.pow(x - p, 2)) 
        #
        # But this form is very slow in "painting" and thus could be missing
        # out some constants (from what I see in other source code), so I'll
        # replicate the same normalization constant as used in style loss.
        return (1 / (4 * N * M)) * tf.reduce_sum(tf.pow(x - p, 2))
    return _content_loss(sess.run(model['conv4_2']), model['conv4_2'])

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
# Layers to use. We will use these layers as advised in the paper.
# To have softer features, increase the weight of the higher layers
# (conv5_1) and decrease the weight of the lower layers (conv1_1).
# To have harder features, decrease the weight of the higher layers
# (conv5_1) and increase the weight of the lower layers (conv1_1).
STYLE_LAYERS = [
    ('conv1_1', 0.5),
    ('conv2_1', 1.0),
    ('conv3_1', 1.5),
    ('conv4_1', 3.0),
    ('conv5_1', 4.0),
]
def style_loss_func(sess, model):
    """
    Style loss function as defined in the paper.
    """
    def _gram_matrix(F, N, M):
        """
        The gram matrix G.
        """
        Ft = tf.reshape(F, (M, N))
        return tf.matmul(tf.transpose(Ft), Ft)
    def _style_loss(a, x):
        """
        The style loss calculation.
        """
        # N is the number of filters (at layer l).
        N = a.shape[3]
        # M is the height times the width of the feature map (at layer l).
        M = a.shape[1] * a.shape[2]
        # A is the style representation of the original image (at layer l).
        A = _gram_matrix(a, N, M)
        # G is the style representation of the generated image (at layer l).
        G = _gram_matrix(x, N, M)
        result = (1 / (4 * N**2 * M**2)) * tf.reduce_sum(tf.pow(G - A, 2))
        return result
    E = [_style_loss(sess.run(model[layer_name]), model[layer_name]) for layer_name, _ in STYLE_LAYERS]
    W = [w for _, w in STYLE_LAYERS]
    loss = sum([W[l] * E[l] for l in range(len(STYLE_LAYERS))])
    return loss

一開始給定 random input image:

style image 選定如下:

隨著 iteration 增加會像這樣:

  • 第一次的 backprob:
  • 1000 iteration:
  • 2000 iteration:
  • 3000 iteration:
  • 4000 iteration:
  • 5000 iteration:

短節

這之間很多參數可以調整去玩, 有興趣可以自己下載 gitHub 去測

上一篇的 “GTX 1070 參見” 有提到, 原來用 CPU 去計算, 1000 iteration 花了六個小時! 但是強大的 GTX 1070 只需要 6 分鐘!

不過, 就算是給手機用上GTX1070好了 (哈哈當然不可能), 6分鐘的一個結果也是無法接受!
PRISMA 可以在一分鐘內處理完! 這必定不是這種要算 optimization 的方法可以達到的.
事實上, 李飛飛的團隊發表了一篇論文 “Perceptual Losses for Real-Time Style Transfer and Super-Resolution“
訓練過後, 只需要做 forward propagation 即可! Standford University 的 JC Johnson 的 gitHub 有完整的 source code!
找時間再來寫這篇心得文囉!