Motion Models
資料為 Udacity 課程內容
在上一篇 EKF 中,我們其實假設的是 constant velocity model (CV),也就是如下的關係式
$$\begin{align}
x_k = Fx_{k-1}+\nu_k \\
x_k=
\left(
\begin{array}{clr}
p_x \\
p_y \\
v_x \\
v_y
\end{array}
\right),
F=
\left(
\begin{array}{clr}
1 & 0 & \Delta{t} & 0 \\
0 & 1 & 0 & \Delta{t} \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{array}
\right)
\end{align}$$
正好滿足 Kalman Filter 中 State-space model 的假設,但這樣的 motion model 很明顯太單純了,因為車子總是在變速且轉彎。因此真實在使用的時候不會用 CV model,那會用什麼呢? 以下為幾種可用的:
- constant turn rate and velocity magnitude model (CTRV)
- constant turn rate and acceleration (CTRA)
- constant steering angle and velocity (CSAV)
- constant curvature and acceleration (CCA)
Udacity 在這次的 project 中讓我們使用了 CTRV,而此 model 的 state vector $x$ 定義如下:
$$\begin{align}
x=
\left(
\begin{array}{clr}
p_x \\
p_y \\
v \\
\psi \\
\dot{\psi}
\end{array}
\right)
\end{align}$$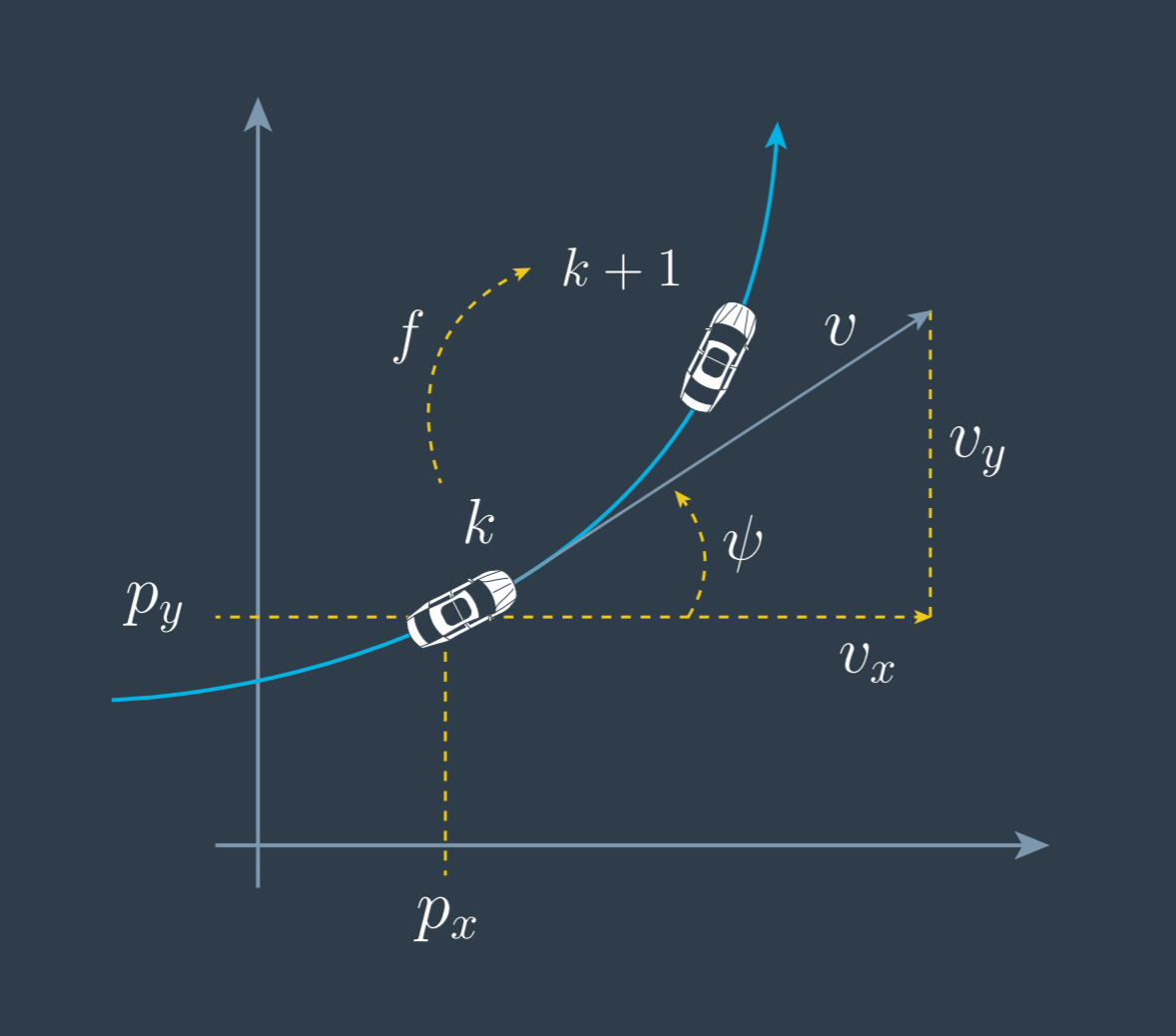
其中 $p_x,p_y$ 是 $x,y$ 座標位置,$v$ 是速度的 magnitude,$\psi$ 是速度的向量與水平軸的夾角稱 yaw angel,最後的 $\dot{\psi}$ 則是該夾角的變化率稱 yaw rate。
而 CTRV 假設的是 $v$ 和 $\dot{\psi}$ 是 constant。而此 model 已不是一個線性系統了,也就是無法用 matrix 來表達,所以我們將式(1)改為如下的表達方式:
$$\begin{align}
x_{k+1} = f(x_k,\nu_k)
\end{align}$$
如何將 function $f$ 寫成遞迴式子呢? 請看下一段
CTRV State Vector Recursion
我們先忽略 noise $\nu_k$ 這項,晚點再加回來。State vector 隨時間變化的式子如下:
$$\begin{align}
x_{k+1}=x_k+\int_{t_k}^{t_{k+1}}{
\left[
\begin{array} \\
\dot{p}_x(t) \\
\dot{p}_y(t) \\
\dot{v}(t) \\
\dot{\psi}(t) \\
\ddot{\psi}(t)
\end{array}
\right]
}dt\\
x_{k+1}=x_k+
\left[
\begin{array}{center}
\int_{t_k}^{t_{k+1}}{v(t)\cdot cos(\psi(t))}dt \\
\int_{t_k}^{t_{k+1}}{v(t)\cdot sin(\psi(t))}dt \\
0 \\
\dot{\psi}_k\cdot\Delta{t} \\
0
\end{array}
\right]
\end{align}$$
注意到 CTRV 的假設 $v$ 和 $\dot{\psi}$ 是 constant,也就會造成式(5)中 $\dot{v}(t)=\ddot{\psi(t)}=0$,且從時間 $k$ 到 $k+1$ 的 $\dot{\psi}(t)$ 都等於 $\dot{\psi}_k$,也因此得到式(6)。
但是我們仍然要處理式(6)前兩項的積分,首先一樣基於CTRV假設 $v(t)=v_k$ 對於時間 $k$ 到 $k+1$ 都是一樣,所以提到積分外面。然後由於 yaw rate 是 constant,因此 $\psi(t)$ 可以明確表示出來,總之改寫如下:
$$\begin{align}
x_{k+1}=x_k+
\left[
\begin{array}{center}
v_k\int_{t_k}^{t_{k+1}}{cos(\psi_k+\dot{\psi}_k\cdot(t-t_k))}dt \\
v_k\int_{t_k}^{t_{k+1}}{sin(\psi_k+\dot{\psi}_k\cdot(t-t_k))}dt \\
0 \\
\dot{\psi}_k\cdot\Delta{t} \\
0
\end{array}
\right]
\end{align}$$
然後沒什麼好說的,就積它吧:
$$\begin{align}
x_{k+1}=x_k+
\left[
\begin{array}{center}
\frac{v_k}{\dot{\psi}_k}(sin(\psi_k+\dot{\psi}_k\Delta{t})-sin(\psi_k)) \\
\frac{v_k}{\dot{\psi}_k}(-cos(\psi_k+\dot{\psi}_k\Delta{t})+cos(\psi_k)) \\
0 \\
\dot{\psi}_k\cdot\Delta{t} \\
0
\end{array}
\right]
=x_k+Deterministic_k
\end{align}$$
這邊有一個實作上需要避免的地方,就是當 $\dot{\psi}_k=0$ 時,上式的第1,2項會除0。不過我們知道當 $\dot{\psi}_k=0$ 表示車子是直直往前開,yaw angle不會改變,因此實際上可以用如下來計算:
$$\begin{align}
x_{k+1}=x_k+
\left[
\begin{array}{center}
v_kcos(\psi_k)\Delta{t} \\
v_ksin(\psi_k)\Delta{t} \\
0 \\
\dot{\psi}_k\cdot\Delta{t} \\
0
\end{array}
\right]
=x_k+Deterministic'_k
\end{align}$$
Recursion With Noise Term
Noise term $v_k$ 這裡是假設如下:
$$\begin{align}
v_k=
\left[
\begin{array}{center}
v_{a,k} \\
v_{\ddot{\psi},k}
\end{array}
\right]
\end{align}$$
第一個 term 是加速度的 noise,而第二個表示 yaw rate 的變化率。考慮如果有這兩項 noises 的話,並且假設時間 $k$ 到 $k+1$ 這兩個 noises 的值是固定的,那麼 state vector 會變成如下:
$$\begin{align}
x_{k+1}=x_k+Deterministic_k+
\left[
\begin{array}{center}
\frac{1}{2}(\Delta{t})^2cos(\psi_k)\cdot v_{a,k} \\
\frac{1}{2}(\Delta{t})^2sin(\psi_k)\cdot v_{a,k} \\
\Delta{t}\cdot v_{a,k} \\
\frac{1}{2}(\Delta{t})^2\cdot v_{\ddot{\psi},k} \\
\Delta{t}\cdot v_{\ddot{\psi},k}
\end{array}
\right]\\
x_{k+1}=x_k+Deterministic_k+Stochastic_k
\end{align}$$
第三項是速度 $v$ 會被加速度 $v_{a,k}$ 這種 noise 怎麼影響,所以很明顯是線性增加,同理第四和第五項也很容易得到。第一和第二項,$x$ and $y$ 的位置這裡就比較麻煩,因此採用的是一個近似而已。
這邊假設 yaw rate 沒有太高的情況下,下圖的兩個紅色圈圈位置應該是很接近,因此我們可以考慮走直線的紅色圈圈位置,也就得到了(11)第一二項的近似值。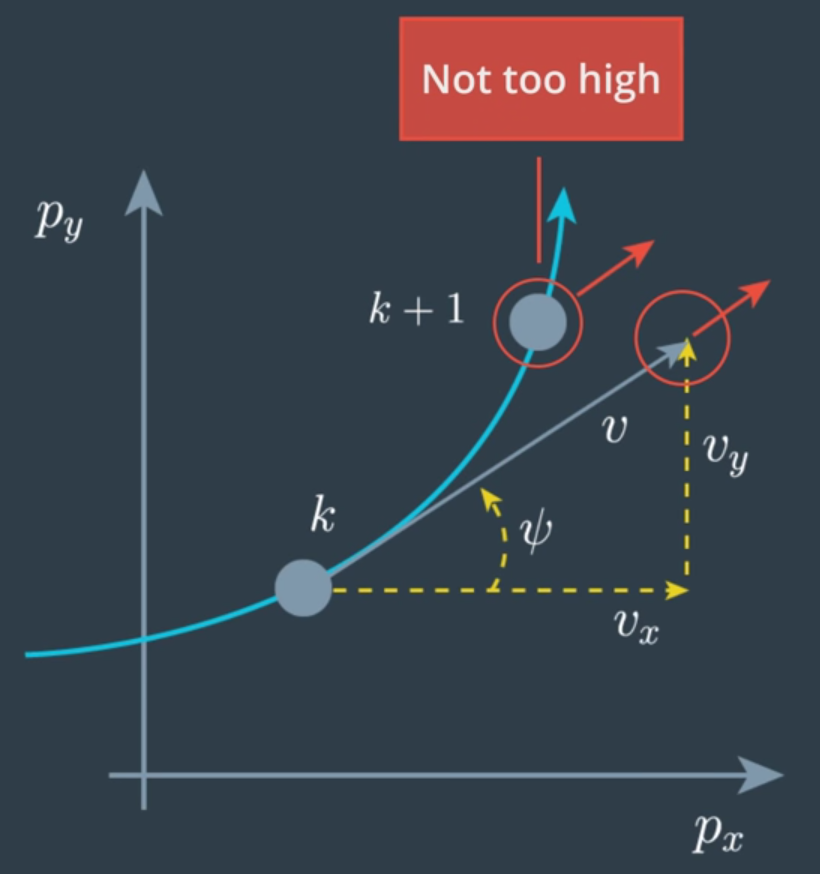
Summary All CTRV
省略解釋,寫出 state recursion 的計算。
$$x=
\left(
\begin{array}{clr}
p_x \\
p_y \\
v \\
\psi \\
\dot{\psi}
\end{array}
\right)$$
if $\dot{\psi}_k\neq0$, then
$x_{k+1}=x_k+Deterministic_k+Stochastic_k$
where
$$Deterministic_k=
\left[
\begin{array}{center}
\frac{v_k}{\dot{\psi}_k}(sin(\psi_k+\dot{\psi}_k\Delta{t})-sin(\psi_k)) \\
\frac{v_k}{\dot{\psi}_k}(-cos(\psi_k+\dot{\psi}_k\Delta{t})+cos(\psi_k)) \\
0 \\
\dot{\psi}_k\cdot\Delta{t} \\
0
\end{array}
\right]$$
and
$$Stochastic_k=
\left[
\begin{array}{center}
\frac{1}{2}(\Delta{t})^2cos(\psi_k)\cdot v_{a,k} \\
\frac{1}{2}(\Delta{t})^2sin(\psi_k)\cdot v_{a,k} \\
\Delta{t}\cdot v_{a,k} \\
\frac{1}{2}(\Delta{t})^2\cdot v_{\ddot{\psi},k} \\
\Delta{t}\cdot v_{\ddot{\psi},k}
\end{array}
\right]$$
otherwise $\dot{\psi}_k=0$, then
$x_{k+1}=x_k+Deterministic'_k+Stochastic_k$
where
$$Deterministic'_k=
\left[
\begin{array}{center}
v_kcos(\psi_k)\Delta{t} \\
v_ksin(\psi_k)\Delta{t} \\
0 \\
\dot{\psi}_k\cdot\Delta{t} \\
0
\end{array}
\right]$$
Unscented Kalman Filter 簡介
由於 CTRV 是非線性的,會破壞 State-space model 的線性假設,例如下圖中原先紅色的高斯分布經過非線性轉換後分布為黃色。不過我們知道 EKF 可以利用 Jaccobian matrix 做線性逼近計算,所以我們同樣可以計算。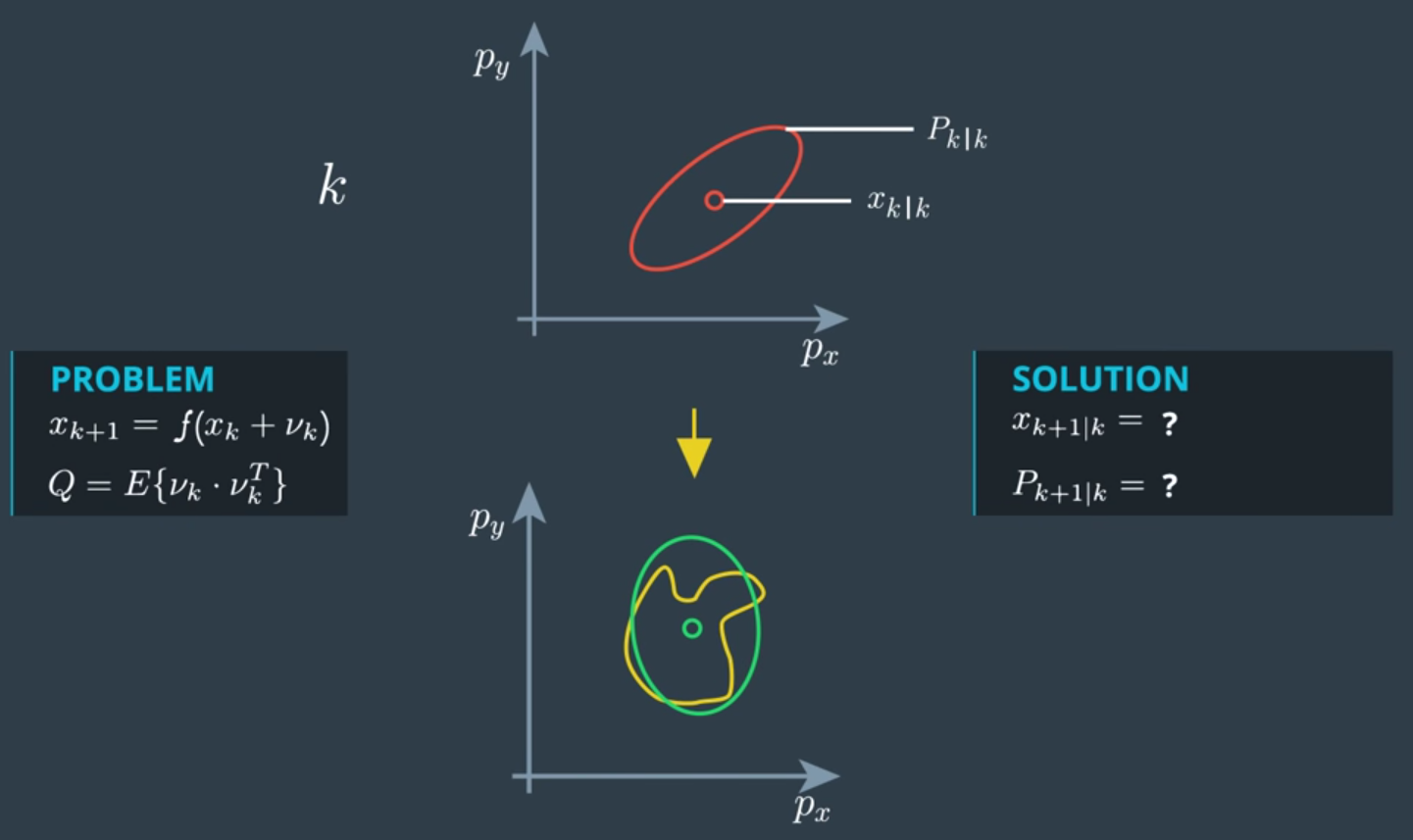
但要計算上述非線性系統的 Jaccobian matrix 實在顯得有點複雜,好在 Unscented KF 可以完全避開這個麻煩。它利用選擇幾個代表的 candidates vectors,叫做 Sigma Points,去計算經過非線性轉換後的值,然後就可以得到 output domain 的 mean 和 covariance matrix,也就是上圖的綠色高斯分布。
這邊要注意的是,output domain 的真實分佈不是高斯分布(黃色),但我們仍然將它當成是高斯分布(綠色)去計算 mean 和 covariance matrix,因為這樣才能繼續套用 Kalman filter 的方法。說到這可知道 UKF 仍然只是逼近,不過根據 Udacity 的說法,實際應用上 UKF 是很快 (不用計算 Jaccobian) 且實際上效果很好!
下回預告,UKF完整介紹。