資料為 Udacity 課程內容。事實上 UKF 挺囉嗦的,單純看本文應該無法理解,必須搭配前兩篇 KF and EKF 和 CTRV。主要是筆記用,讓自己可以根據文章完整實做出來。
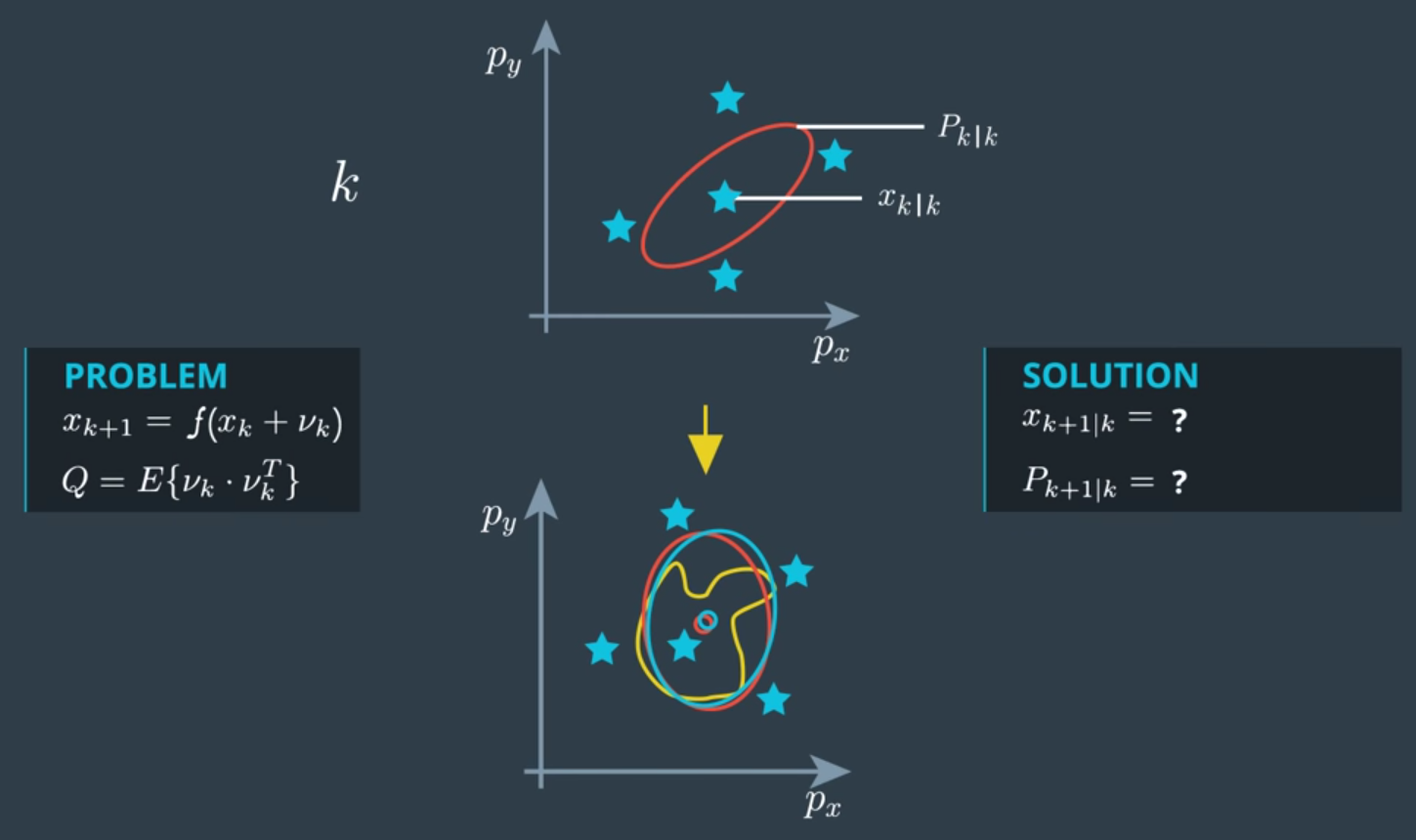
一切的一切都來自於 Kalman Filter 的 State-Space model 假設,我們來稍微回顧一下。
$$\begin{align} x_k = F_kx_{k-1}+\nu_k \\ z_k = H_kx_k+\omega_k \\ \end{align}$$式(1)表示狀態值 $x$ 滿足線性的遞迴關係式,而式(2)表示觀測值 $z$ 是當下狀態值的線性關係式。這個線性的關係式是為了使得我們的高斯分布在轉換後仍然滿足高斯分布所做的假設。但實際上常常不滿足線性的關係,例如假設我們的 $x$ 包含了 Cartesian coordinate 的座標位置和速度的資訊,但是 RADAR 的觀測值 $z$ 卻是用 Polar coordinate 來表示,就會有一個非線性的座標轉換。另一個會造成非線性的情況是發生在式(1),也就是我們如果使用更精確的 motion model,如 CTRV。
EKF 解決的方法是用 Jacobian 做線性的逼近,但是非線性的關係式如果一複雜,算 Jacobian 就會太複雜且造成運算速度變慢。因此,本篇要介紹的 Unscented KF 有相對簡單的辦法,並且運算速度快,且實際效果好。
UKF 概念上怎麼做呢? 我們看上圖就可了解,首先原始的高斯分布(上面的紅色橢圓),經由非線性轉換 $f$ 後得到的 “實際分佈” 為下面的黃色曲線,而該實際分布的 mean 和 covariance matrix 所形成的的高斯分布為下面的紅色橢圓,但是我們不容易得到! 那麼怎麼逼近下面的紅色橢圓呢? UKF 做法就是在上圖選擇一些代表的點,稱為 Sigma Points,經過 $f$ 轉換後,可以得到下面的星星,然後就可以根據這些轉換後的星星去計算他們的 mean 和 covariance matrix,而得到藍色的橢圓。那麼我們馬上開始說明如何設定 Sigma Points 吧。
Sigma Points 選擇
假設 state dimension 為 $n_x$,Sigma Points 就選擇 $2n_x+1$ 個點。我們以 $n_x=2$ 來舉例說明會比較清楚,而擴展到更高的維度也就非常 trivial 了。
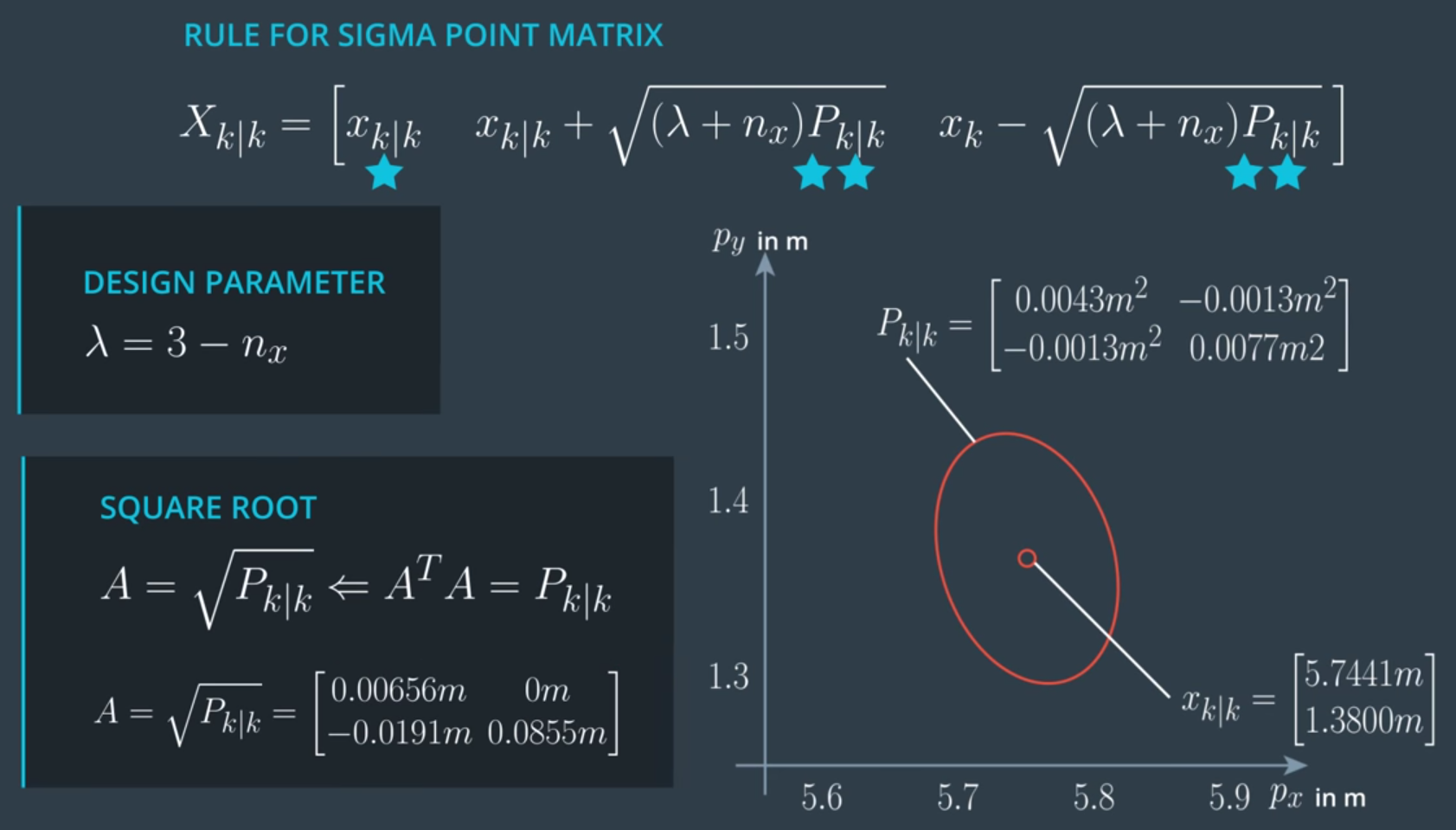
可以知道我們需選擇5個點($2n_x+1$),第一個點是 mean vector,接著針對每一個 dimension 都根據 mean vector 向該 dimension 去做正負方向的 perturb,而 $\lambda$ 表示要 perturb 多遠(使用者給定的值)。但是要特別注意的是,這裡的 perturb dimension 必須是正規化後的方向 (Whitening),否則若原來的高斯分布某一個方向特別大(想像一個很扁的橢圓),使用原來的 covariance matrix 就會被該方向 dominate。上例的 sigma points 如下:
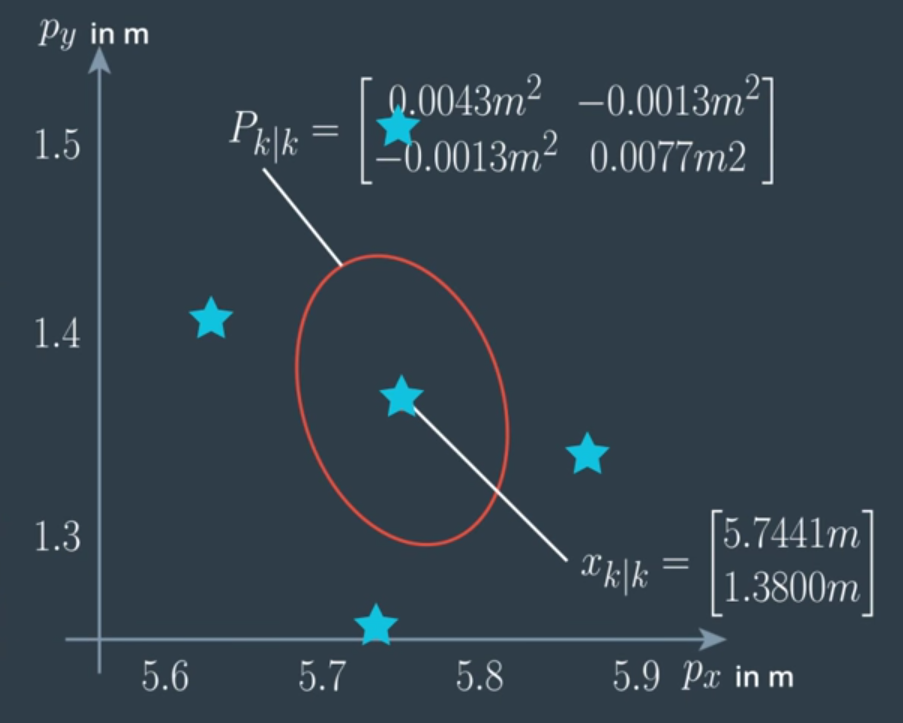
CTRV Sigma Points
我們來看 CTRV model 下的 sigma points 選擇,其中 state vector and noise term 分別定義如下
$$\begin{align} x= \left( \begin{array}{clr} p_x \\ p_y \\ v \\ \psi \\ \dot{\psi} \end{array} \right) \end{align}$$ $$\begin{align} v_k= \left[ \begin{array}{center} v_{a,k} \\ v_{\ddot{\psi},k} \end{array} \right]\\ v_{a,k}\sim N(0,\sigma_a^2),v_{a,k}\sim N(0,\sigma_{\ddot{\psi}}^2) \\ Q=E[v_k,v_k^T]= \left[ \begin{array}{clr} \sigma_a^2 & 0 \\ 0 & \sigma_{\ddot{\psi}}^2 \\ \end{array} \right] \end{align}$$$v_k$ 的第一個 term 是加速度的 noise,而第二個表示 yaw rate 的變化率。由於原始的 state recursion 還參雜了 $Stochastic_k$ 這樣的 vector (參考式(7)and(8)),因此要計算他們的 covariance matrix 會太難搞! (因為我們需要知道 covariance matrix 才能對每個 whitening 後的維度去 perturb 取點)
$$\begin{align} x_{k+1}=x_k+Deterministic_k+ \left[ \begin{array}{center} \frac{1}{2}(\Delta{t})^2cos(\psi_k)\cdot v_{a,k} \\ \frac{1}{2}(\Delta{t})^2sin(\psi_k)\cdot v_{a,k} \\ \Delta{t}\cdot v_{a,k} \\ \frac{1}{2}(\Delta{t})^2\cdot v_{\ddot{\psi},k} \\ \Delta{t}\cdot v_{\ddot{\psi},k} \end{array} \right]\\ x_{k+1}=x_k+Deterministic_k+Stochastic_k \end{align}$$
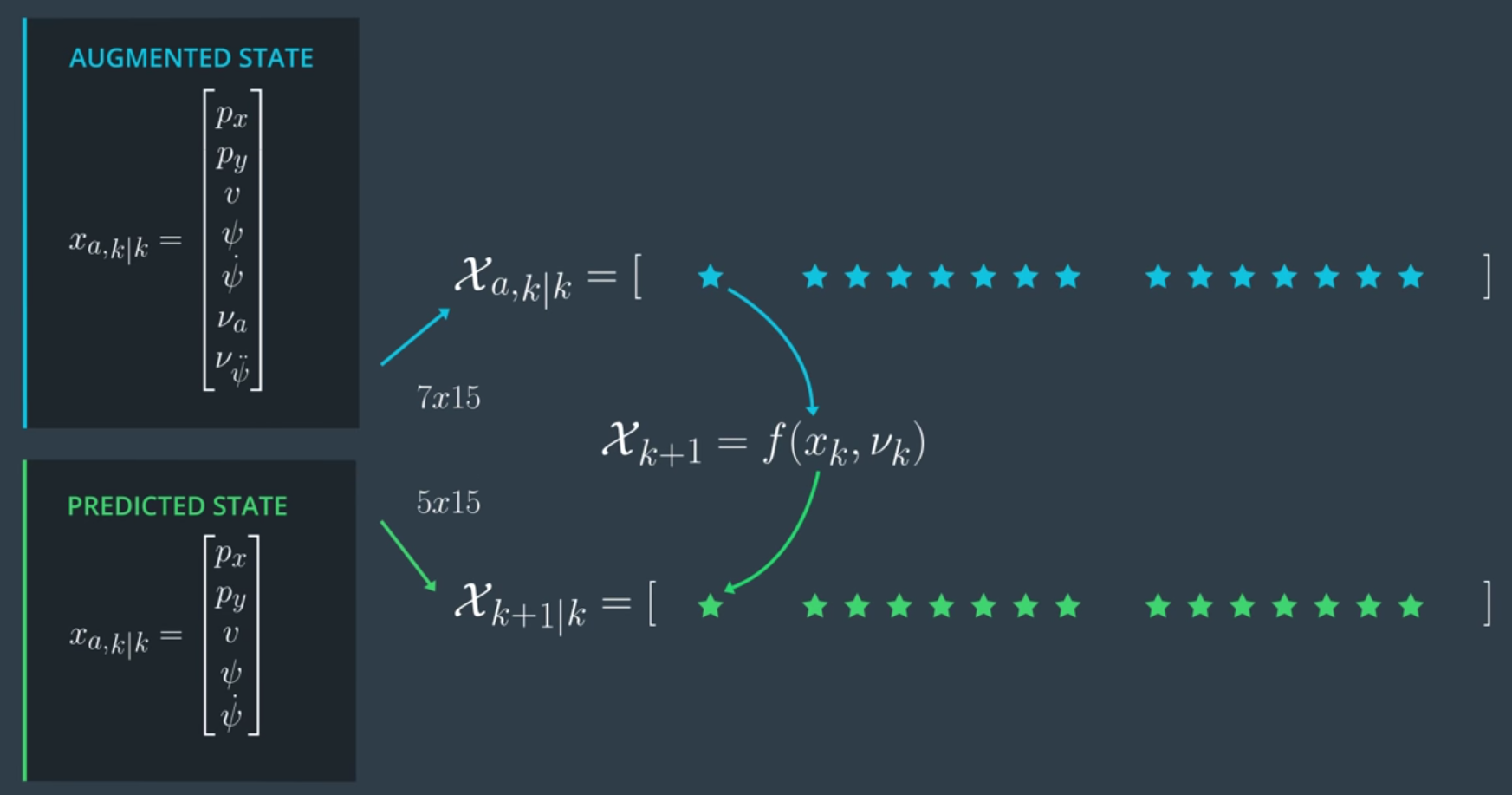
比較簡單的作法是將 noise term (式(4)) 當成 state vector 的另外的維度,主要的好處是 covariance matrix 就變得很容易計算了。然後一樣用上述的方式產生 Sigma Points。因此整個流程如下圖:

可以看到原本維度從5變成7,因此要產生15點的 sigma points,而 augmentated state vector 的 covariance matrix 變得很容易定義。
Sigma Points Prediction
產生了這些 sigma points 之後,我們就可以透過式(7),做 nonlinear recursion 到下一個時間點的 state vector (注意到 noise term 也被 sigma points 取樣了,所以可以帶入式(7)中)!
Mean and Covariance of Sigma Points
還記得嗎? 將 sigma point transform 後,我們下一步就是要估計出 mean 和 covariance,忘記的同鞋們可以看一下本文最開始的圖 (藍色的高斯分布)。
基本上根據一些 data points 算它們的高斯分布非常簡單,但是由於我們當初取的 sigma points 它們之間本來的機率就不同,因此在計算轉換後的高斯分布必須要考慮每個點的權重。權重的設定有不同方法,課程直接建議下面的設定,所以沒特別要說明的,就照公式計算而已:

Measurement Prediction
對於 RADAR 來說式(2)也是一個非線性的關係,因此也可以用 sigma points 的方法來逼近。假設我們在時間點 $k$ 取的 sigma points 為 $x$,經過非線性 state recursion 後得到時間點 $k+1$ 的 sigma points 為 $x’$,我們可以直接將 $x’$ 當作新取的 sigma points,拿來做 measurement 非線性轉換 $z’=h(x’)+w$,然後一樣用上面的公式算一下 measurement space 的高斯分布即可。RADAR 的 $h()$ 定義如下:
$$\begin{align} z=h(x)= \left( \begin{array}{clr} \rho \\ \phi \\ \dot{\rho} \end{array} \right) = \left( \begin{array}{clr} \sqrt{p_x^2+p_y^2} \\ \arctan(p_y/p_x) \\ \frac{p_xcos(\psi)v+p_ysin(\psi)v}{\sqrt{p_x^2+p_y^2}} \end{array} \right) \end{align}$$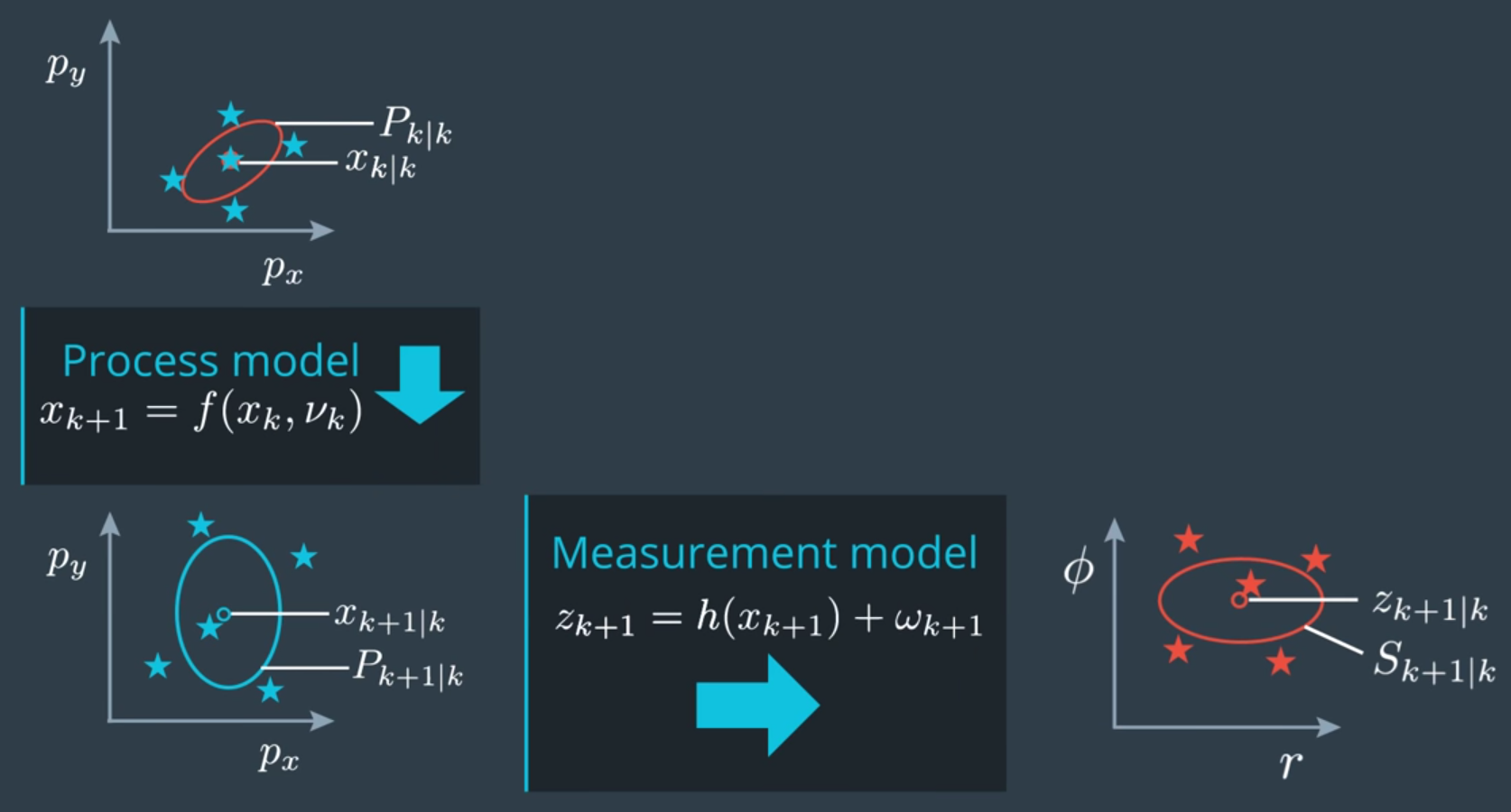
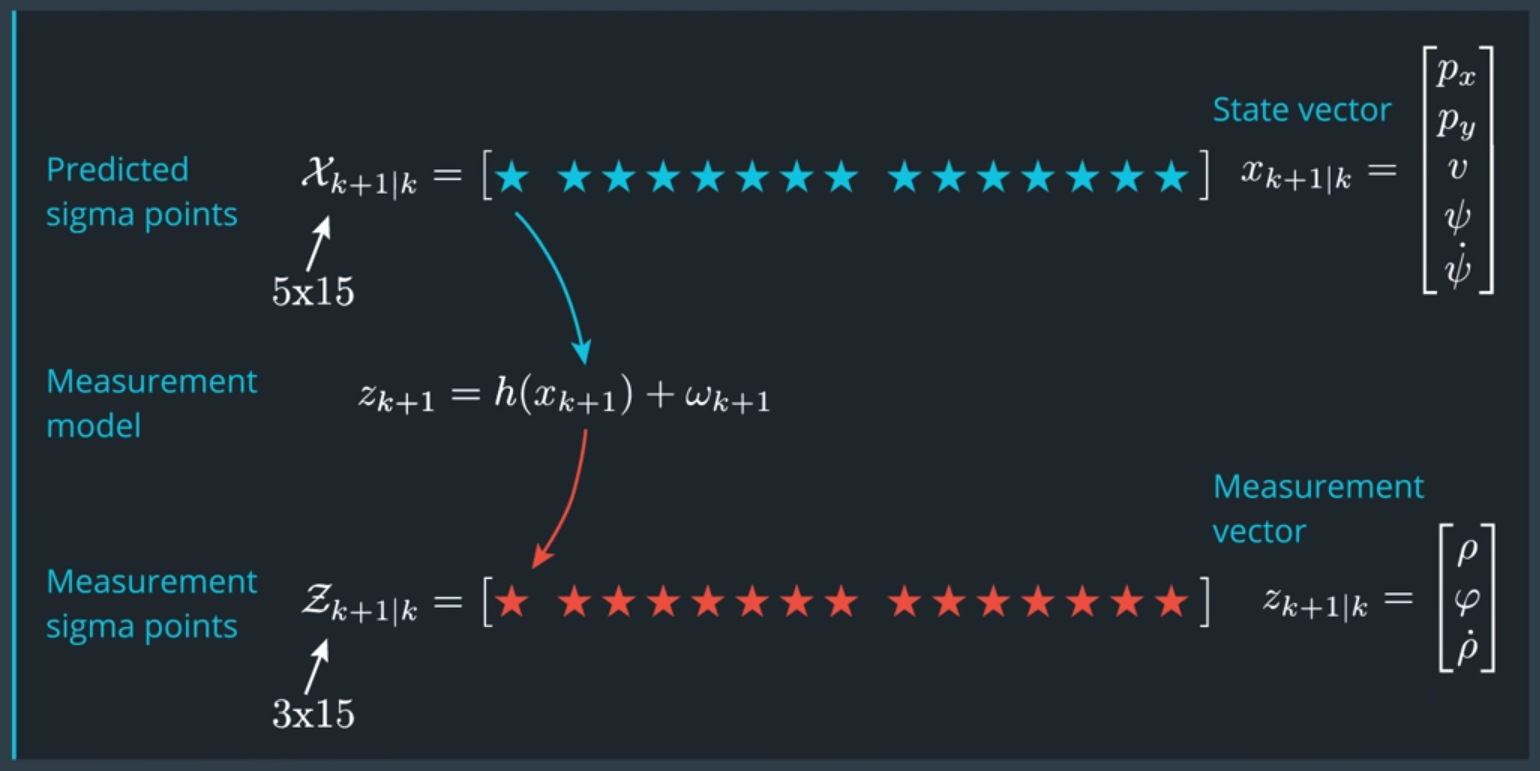
稍微要注意的是,計算 covariance 時須考慮 noise 的 covariance (下圖紅色框起來的地方),這跟計算 state space 中的高斯分布不同。這是因為在 measurement space 是兩個 independent 的高斯分布相加 (一個是 sigma point 估出來的,另一個是 noise 的高斯),covariance 就是相加而已。
另外對於 LIDAR 來說 measurement 的轉換是線性關係,所以不使用 sigma point 的方法,因此在處理兩種 sensor data 時,記得區分一下 case。
Measurement Update
終於來到最後的步驟了。我們費盡千辛萬苦根據時間點 $k$ 的 state vector 估計出了時間點 $k+1$ 的 measurement 值,而此時我們在時間點 $k+1$ 也收到了真正的 sensor data measurement。因此同樣可以使用 KF 的流程去計算所有的 update! 原因是我們其實全部都高斯化了 (透過 sigma points 方法)。

紅色框起來處為跟以前不同的地方,變成要計算 cross-correlation of “Measurement Prediction 那個 section 的第二張圖那兩排的 vectors”
心得
其實概念並不困難,但是頗多計算流程和符號,同時也必須先了解 Kalman Filter 和 CTRV motion model,下一步就實作 Project 吧!
附上 predict 的結果:
