統一的框架 Bayes Filter

發表於 | 分類於 | [object Object]

Bayes Filter Introduction

前幾篇討論了很多 Kalman Filter 以及它相關的變形，如: EKF and UKF。這些方法我們都可以放在 Bayes Filter 的框架下來看，這麼做的話，KF 就只是其中一個特例了 (都是高斯分布的情形)。而如果我們只考慮幾個離散點的機率，並用蒙地卡羅法來模擬取樣的話，這種實作方式就會是 Particle Filter 。所以掌握了 Bayes Filter 背後的運作方式對於理解這些方法是很有幫助的。
一些變數的意義仍然跟前幾篇一樣:

  • z: measurement，也就是我們實際上經由 sensor 得到的測量值 (會有noise)
  • x: state，我們希望估計出來的值，在 Localization 一般就是座標值

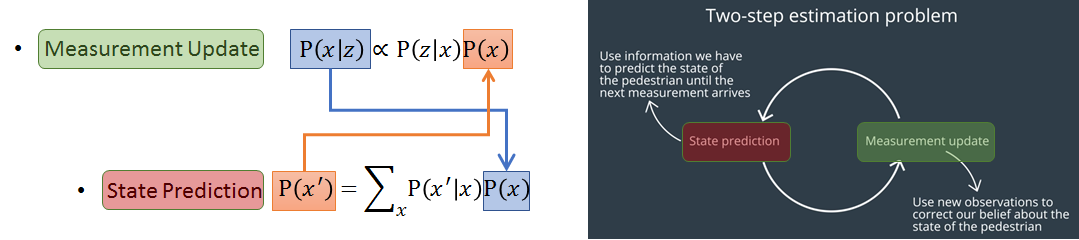
發現了嗎? 在上圖右 KF 的兩個步驟: Measurement Update 和 State Prediction 實際上就是上圖左邊的兩個數學式關係。搭配下圖文字一起看，Measurement Update 理解為得到一個觀察值 $z$ 後，我們用 Bayes Rule 可以估測出 state $x$ 的事後機率 $P(x|z)$，而該事後機率經由 motion model (eg. CTRV) 可以估測出下一個時間點的 x 機率分佈 $P(x’)$ (此步驟為 State Prediction)。得到新的 $P(x’)$ 就可以當成下一個時間點的事前機率，所以 Bayes rule 就可以接著下去重複此 loop。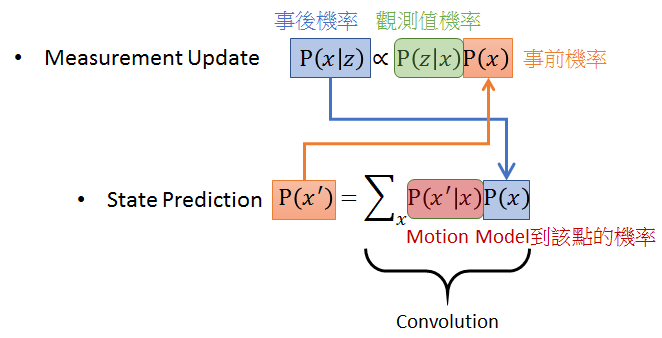

與 Maximum a Posteriori (MAP) Adaptation 的關係

事實上，這樣的框架也跟 MAP Adaptation 息息相關! 例如當事前機率是某些特別的機率分佈 (exponential family)，經由 Bayes rule 得到的事後機率，它的機率分佈會跟事前機率是同一類型的，(例如都是 Gaussian)。而這樣的選擇我們稱為 conjugate prior。由於 “事後” 與 “事前” 機率是同一種類型的機率分佈，因此把 “事後機率” 在當成下一次資料來臨時的 “事前機率” 也就很自然了! 這就是 MAP Adaptation 的核心概念，與 Bayes filter 一模一樣阿!

Localization 詳細定義

好的，我們來針對 Localization 詳細解釋吧，名詞定義如下:

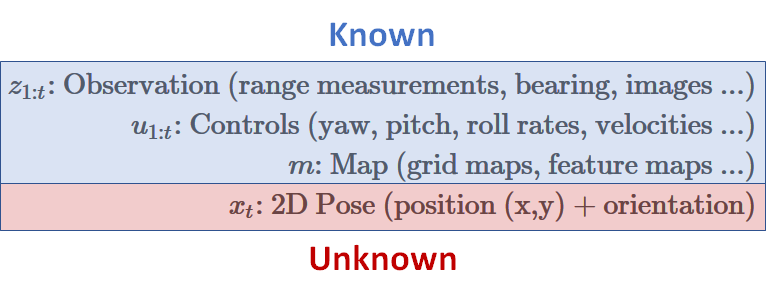
觀測值 (time 1~t)、控制 (time 1~t)、和地圖 $m$ 都是假設已知，我們所不知的(要估測的)是目前 time t 的狀態值 $x$。
舉例來說，一個一維的地圖如下: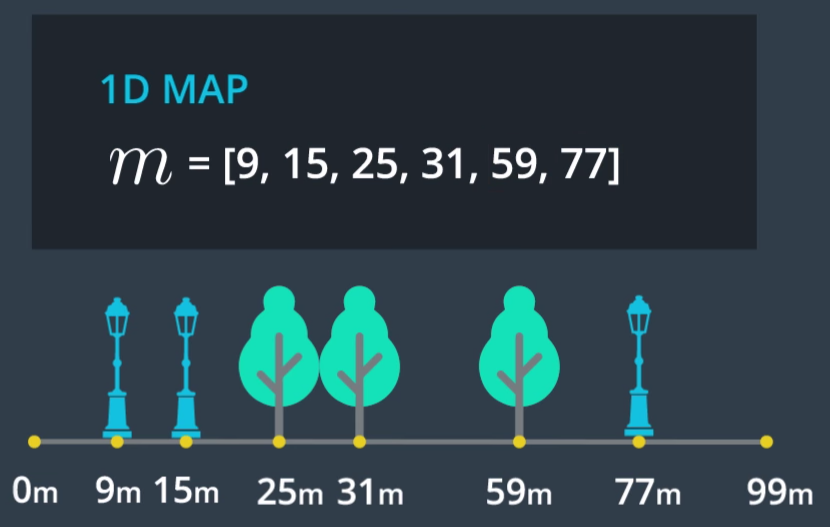

而觀測值 $z_{1:t}$ 如下: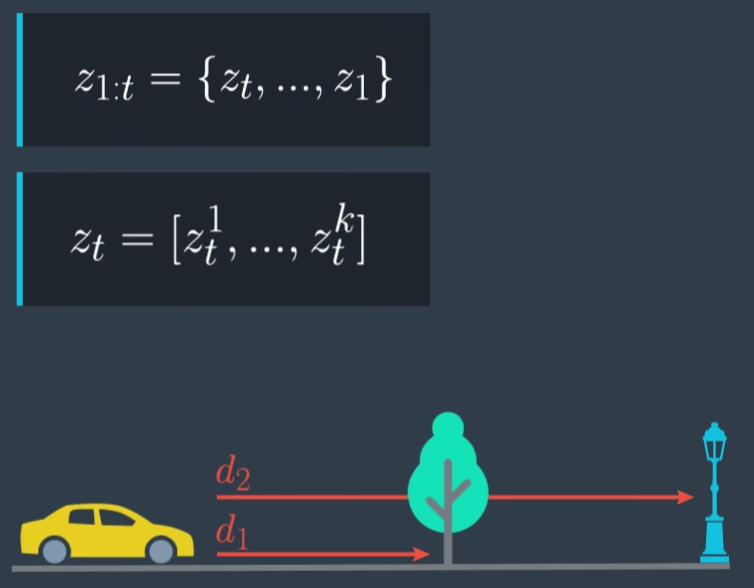

可以知道每一個時間點的觀測值是一個 dimension 為 k 的向量。

整個 Localization 的目的就是要計算對於位置 $x$ 我們有多少信心度，嚴謹地說，我們就是要計算如下:
$$\begin{align} bel(x_t)=p(x_t|z_{1:t},u_{1:t},m) \end{align}$$

意思是在已知目前所有的觀測值、控制、和地圖的情況下，位置 $x_t$ 的機率是多少，看數學式子的話，這不就正好就是 事後機率 嗎? 所以上面的 Bayes filter 架構就有發揮的空間了。另外一提的是，如果將地圖 $m$ 也當成未知的話，就是 SLAM 演算法了。(還沒有機會去讀這個演算法)
下圖是一個一維的示意圖: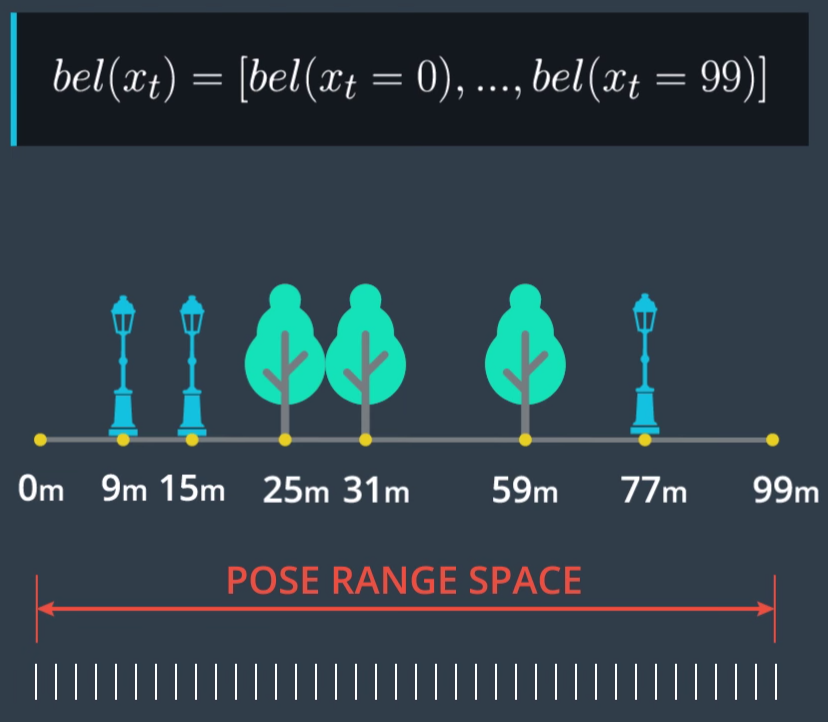

但是要計算這樣的事後機率，必須要考慮從一開始到目前時間點的所有觀測值和控制，這樣的資料量實在太大，計算會非常沒有效率。因此，如果能只考慮目前的觀測值和控制，並用上一個時間的的事後機率就能推算出來的話，勢必會非常有效率。簡單來講，我們希望用遞迴的方式: 考慮 $bel(x_{t-1})$ 和目前的觀測值 $z_t$ 和控制 $u_t$ 就能推算 $bel(x)$。
這就必須要簡化上面 $bel(x_t)$ 原始的定義了，要如何達到呢? 需借助 First-order Markov Assumption 。

First-order Markov Assumption 簡化 believe

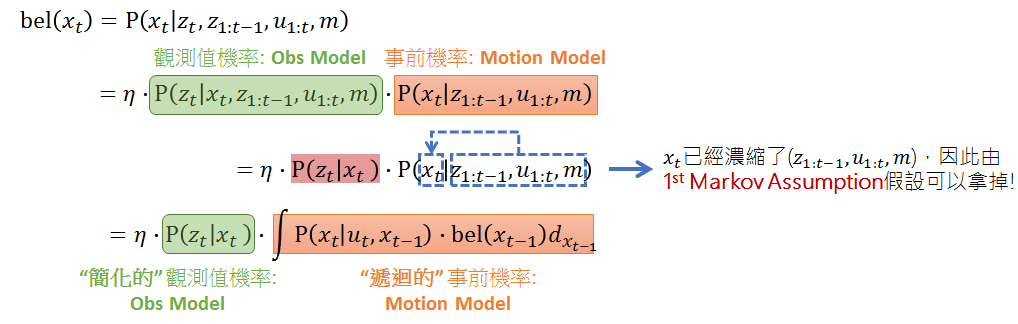
假設目前的時間點為 $t$，我們知道要計算的 believe $bel(x_t)$ 代表事後機率，再套用 Bayes rule 之後，可以得到上面的表示。

  • 事後機率 (Believe): 特別把時間點 t 的觀測值從原先定義拉出來，這是要強調我們在得到最新的觀測值 $z_t$ 後，希望去計算最新的 believe
  • 事前機率 (Motion Model): 稱為 Motion Model 是因為假設我們目前在時間點 $t-1$，接著拿到下一次的控制 $u_t$ 後，我們希望估測出下一次的狀態值 $x_t$ 是什麼。有看過前幾篇的讀者應該馬上就能想到，可以利用 CTRV 之類的 motion model 去計算。
  • 觀測值機率 (Observation Model): 這個是要計算當下的觀測值的機率分佈，這部分通常就是經由 sensor data 得到後，我們假設是高斯分布來計算。

Motion Model 遞迴

我們發現到，最後一行的結果，對照本文第一張圖的 State Prediction 式子是一樣的意思，差別只在一個是連續一個是離散。另一個差別是，此式子明顯寫出可以用上一次的事後機率做遞迴，所以第一張圖的 Measurement Update 藍色箭頭就這麼來的。

Observation Model 簡化

Bayes Filter Summary

重新整理一下經由 “Motion Model 遞迴” 和 “Observation Model 簡化” 過後的事後機率 $bel(x_t)$，結果如下圖左。 (下圖右只是列出本文最開始的 Bayes Filter 式子來做對照)。結論是我們花了那麼大的力氣，用上了 1st Markov Assumption 去處理 Localization 的遞迴式子和簡化，結果不意外地就如同開始的 Bayes Filter 一樣。

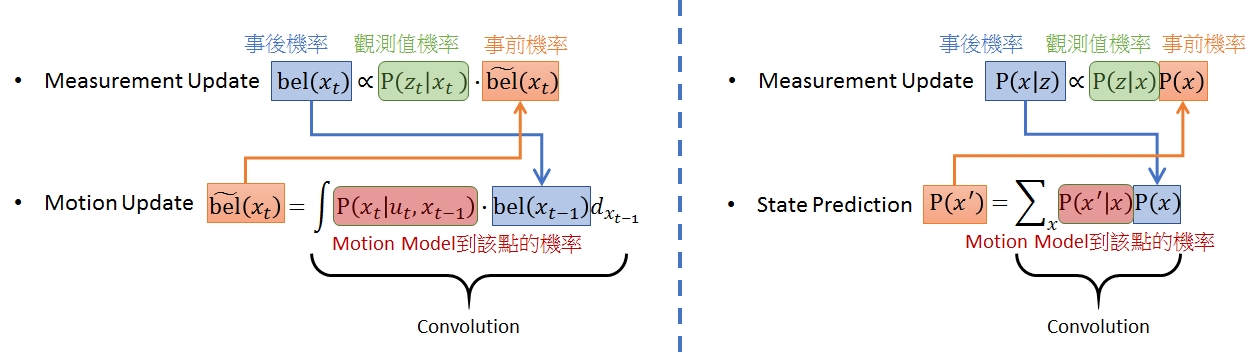
另外，實作上如果所有的 pdf 都是高斯分布的話，結果就是 Kalman Filter。而如果透過 sampling 離散的狀態位置的話，結果就會是 Particle Filter。這部分就先不多說明了。(附上課程一張截圖)

有關 Particle Filter 的實作，在 Udacity Term2 Project3 中我們實作一個二維地圖的 localization。相關 Codes 可在筆者 github 中找到。

Reference