記得當年念博的時候,對於SVM頗有愛,也覺得掌握度很高惹,就是 kernel method + convex optimization 的完美合體。直到某天看到 structureSVM,看了老半天實在不得要領,當時就放下沒再管了。多年後 (2015),剛好台大李宏毅教授教的課程最後一堂 Project demo,有請我們部門介紹做的一些內容給學生,才看到了強大的李老師的課程內容。他所教的 structure learning/svm 實在有夠清楚,又非常 general,真的是強到爆! 本人又年輕,又謙虛,我的新偶像阿!
附上一張我與新偶像的合照… XD

以下內容為筆記用,方便日後回想,來源 大都是李老師的內容。
A General Framework (Energy-based Model)
一般來說 ML 要學習的是 $f:\mathcal{X}\rightarrow\mathcal{Y}$ 這樣的一個 mapping function,使得在學習到之後,能夠對於新的 input $x$ 求得預測的 $y=f(x)$。簡單的情況是沒問題,例如 binary classification、multi-class classification 或 regression。但是萬一要預測的是複雜得多的 output,譬如 $\mathcal{Y}$ 是一個 tree、bounding box、或 sequence,原來的架構就很難定義了。
所以將要學的問題改成如下的架構。
- Training: $F: \mathcal{X} \times \mathcal{Y} \rightarrow \mathbb{R}$
- Inference: Given an object $x$, $\tilde{y}=argmax_y F(x,y)$
$F$ 可以想成用來計算 $(x,y)$ 的匹配度。而這樣的 function 也稱為 Energy-based model。好了,定義成這樣看起來沒什麼不同,該有的問題還是在,還是沒解決。沒關係,我們繼續看下去,先把三個重要的問題列出來。
- Problem 1: 怎麼定義 $F(x,y)$ ?

- Problem 2: 怎麼解決 $argmax_y$ ?

- Problem 3: 怎麼訓練 $F(x,y)$ ?

這些問題在某種情況會變得很好解,什麼情況呢? 若我們將 $F(x,y)$ 定義成 Linear Model (Problem 1 用 linear 定義),我們發現訓練變得很容易 (Problem 3 好解) !! 疑?! Problem 2呢? 先當作已解吧,ㄎㄎ。
Linear Model of $F(x,y)=w\cdot \phi(x,y)$
我們先假裝 Problem 2 已解 (Problem 2 要能解 depends on 問題的domain,和feature的定義),我們來看一下要怎麼訓練這樣的 linear model。
首先用李老師課程的範例 (辨識初音) 的例子舉例,其中 $y$ 是一個 bounding box: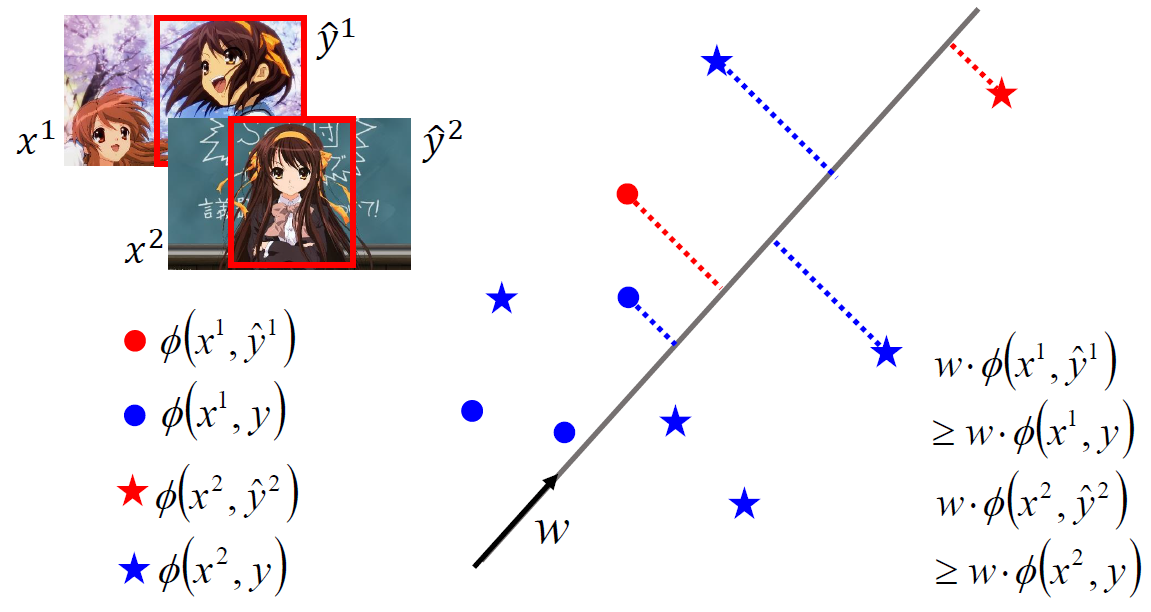
這個例子有兩個 training pairs: $(x^1,\hat{y}^1)$ 和 $(x^2,\hat{y}^2)$,我們希望求得一個 $w$ 使得紅色的圓圈投影到 $w$ 上後要大於所有藍色的圓圈。同理,紅色的星星要大於所有藍色的星星。
其實我們仔細想想,這問題跟 perceptron learning 非常類似,perceptron learning 在做的是 binary classification,而如果把每一筆 training data $(x^i,\hat{y}^i)$ 和 $(x^i,y:y\neq\hat{y}^i)$ 當作是 positive and negative classes,剛好就是一個 bineary classification problem (雖然不同筆 training data 會有各自的 positive and negative 資料,但不影響整個問題)
所以如果有解 (linear separable),則我們可以使用 Structure Perceptron 在有限步驟內求解。
Structure Perceptron

證明的概念跟 perceptron 一樣,就是假設有解,解為 $\hat{w}$,要求每一次的 update $w^k$,會跟 $\hat{w}$ 愈來愈接近,也就是
$$\begin{align} cos\rho_k = \frac{\hat{w}\cdot w^k}{\Vert{\hat{w}}\Vert\cdot\Vert{w^k}\Vert} \end{align}$$要愈大愈好!但我們也知道 $cos$ 最大就 1,因此就有 upper bound,所以會在有限步驟搞定。詳細推倒步驟可參考李老師講義,或看 perceptron 的收斂證明。
Cost Function
用 cost function 的角度來說,其實 perceptron 處理的 cost 是計算錯誤的次數,如果將 cost 的 function 畫出來的話,會是 step function,而無法做微分求解。因此通常會將 cost function 改成可微分的方式,例如 linear or quadratic or what ever continuous function。改成可微分就有很多好處了,可以針對 cost function 做很多需要的修改,這些修改包括 1. 對不同的錯誤有不同的懲罰 2. 加入 regularization term … 等等,我們等下會談到。
Picture is from Duda Pattern Classification
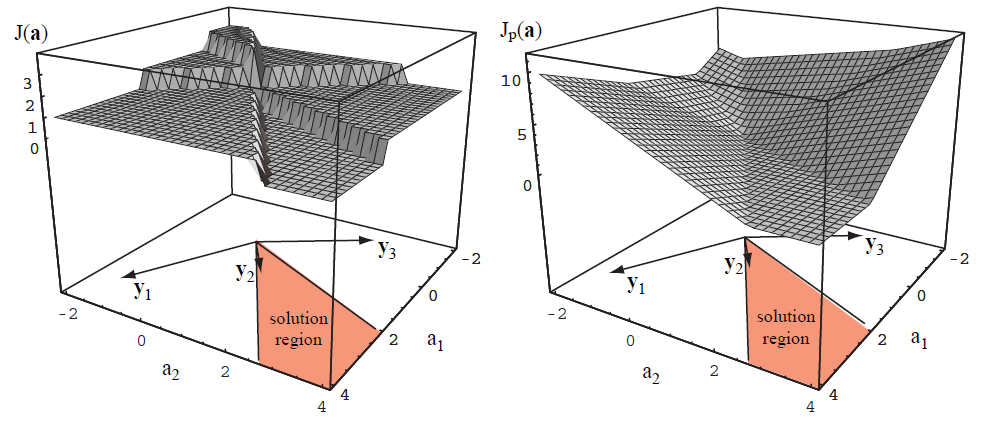
左圖就是原來的 perceptron cost,而右圖就是將 cost 改成 linear cost。
Linear cost 可定義如下:
$$\begin{align}
C=\sum_{n=1}^N C^n \\
C^n=(max_y[w\cdot\phi(x^n,y)])-w\cdot\phi(x^n,\hat{y}^n)
\end{align}$$
所以,就gradient descent下去吧,跟原來的 perceptron learning 改 cost function 一樣。
讓錯誤的程度能表現出來
這是什麼意思呢? 原來的 cost function 對於每一個錯誤的情形都一視同仁,也就是在找那個 $w$ 的時候,只要錯誤的例子投影在 $w$ 上比正確的還要小就好,不在忽小多少,但事實上錯誤會有好壞之分。下面是一個李老師的例子,例如右邊黃色的框框雖然跟正確答案紅框框不同 (所以被當成錯誤的例子),但有大致上都抓到初音的臉了,因此我們可以允許他跟正確答案較接近。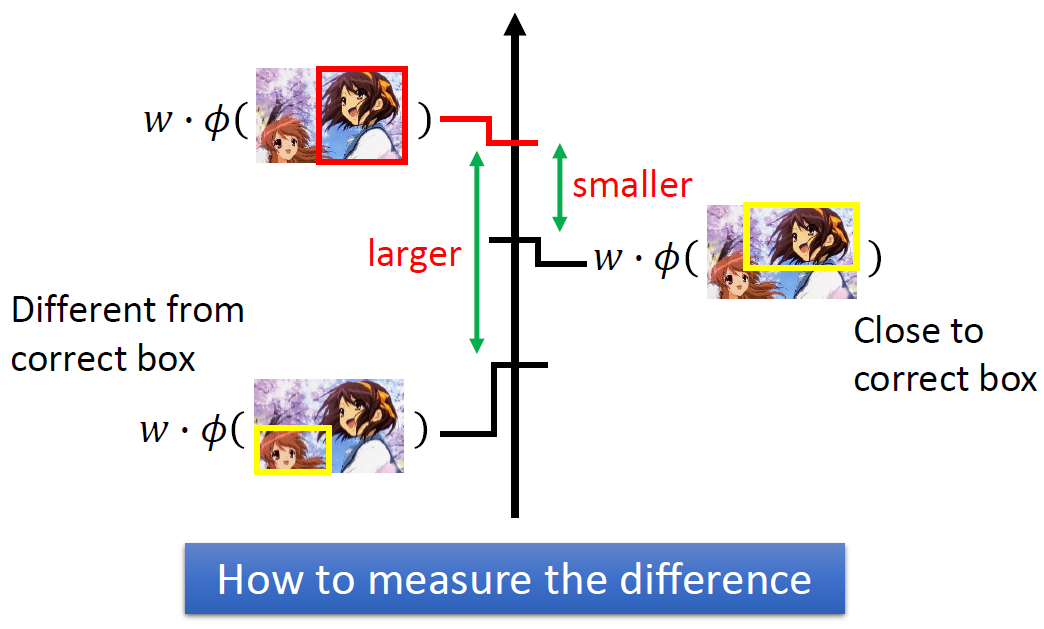
因此 cost function 可以修改一下:
$\triangle(\hat{y}^n,y)$ 定義了這個錯誤的例子額外的 cost (需>=0),以 bounding box 而言,舉例來說兩個 set A and B,$\triangle(A,B)$ 可定義為 $1-/frac{A \cap B}{A \cup B}$。
不過需要特別一提的是,多增加這個額外的定義,有可能使得原來容易解的 $argmax_y$ (Problem 2) 變得無法解,所以要注意。
Minimize the upper bound
很有趣的一點是,在我們引入了 $\triangle(\hat{y}^n,y)$ (稱為 margin, 在後面講到 structure SVM 可以看得出來) 後,可以用另一個觀點來看這個問題。
假設我們希望能將 $C’$ 最小化:
$$\begin{align} \tilde{y}^n=argmax_y{w\cdot \phi(x^n,y)} \\ C'=\sum_{n=1}^N{\triangle(\hat{y}^n,\tilde{y}^n)} \end{align}$$結果我們發現其實 $\triangle(\hat{y}^n,\tilde{y}^n)\leq C^n$,因而變成
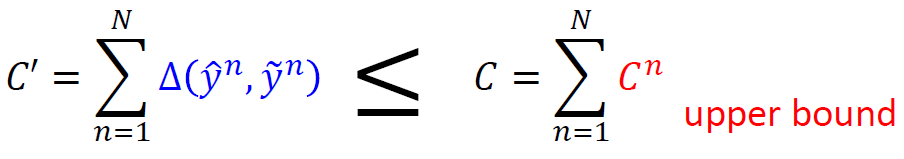
而我們上面都是在最小化 $C$,所以其實我們在做的事情就是在最小化 $C’$ 的 upper bound。
上界的證明如下: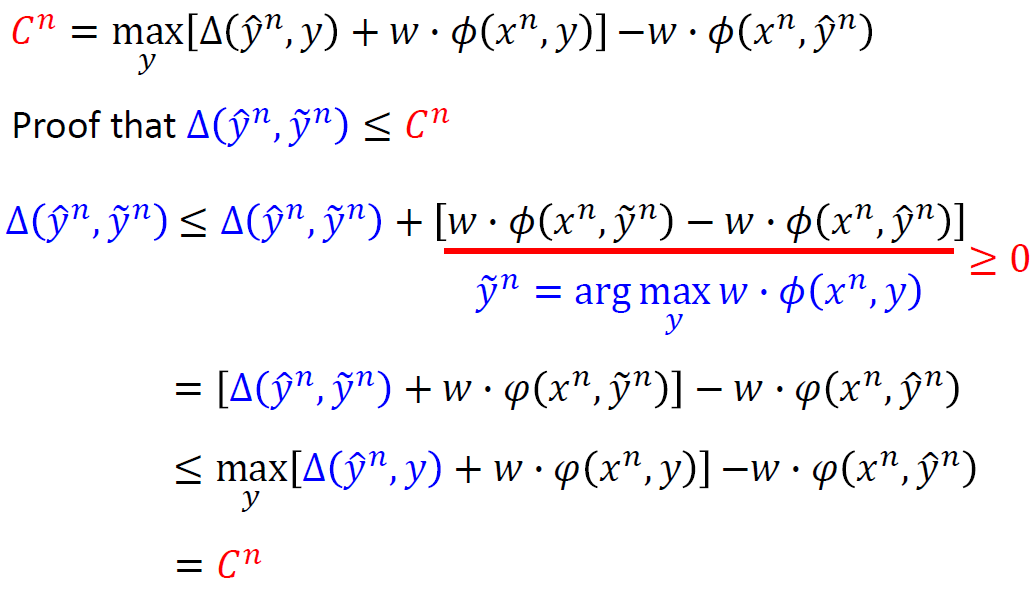
這種藉由最佳化 upper bound 的方式,在 adaboost 也見過。普遍來說,原來的式子不容易最佳化的時候,我們藉由定義一個容易最佳化的upper bound,然後最小化它。另外,EM 演算法也有類似的概念。
Regularization
直接加入 norm-2 regularization:
$$\begin{align}
C=\frac{1}{2}\Vert{w}\Vert ^2+\lambda\sum_{n=1}^N C^n \\
C^n=max_y[w\cdot\phi(x^n,y)+\triangle(\hat{y}^n,y)]-w\cdot\phi(x^n,\hat{y}^n)
\end{align}$$
Structure SVM
先講結論: 上面 Linear Model 最後的 cost function (包含marginal and regularization terms) 就是等價於 SVM。
原先問題 P1:
Find $w$ that minimize $C$
$$\begin{align} C=\frac{1}{2}\Vert{w}\Vert ^2+\lambda\sum_{n=1}^N C^n \\ C^n=max_y[w\cdot\phi(x^n,y)+\triangle(\hat{y}^n,y)]-w\cdot\phi(x^n,\hat{y}^n) \end{align}$$
改寫後的問題 P2:
Find $w$ that minimize $C$
$$\begin{align} C=\frac{1}{2}\Vert{w}\Vert ^2+\lambda\sum_{n=1}^N C^n \\ For \forall{y}: C^n\geq w\cdot\phi(x^n,y)+\triangle(\hat{y}^n,y)-w\cdot\phi(x^n,\hat{y}^n) \end{align}$$
觀察 P2,我們注意到給定一個 $w$ 時,它最小的 $C^n$ 應該會是什麼呢? (找最小是因為我們要 minimize $C$) 譬如我要求 $x\leq{ 5,1,2,10 }$ 這個式子的 $x$ 最小是多少,很明顯就是 $x=max{ 5,1,2,10 }$。因此式 P2 的式 (13) 可以寫成 P1 的式 (11)。
寫成 P2 有什麼好處? 首先將 $C^n$ 改成 $\epsilon^n$,然後再稍微改寫一下得到如下的問題:
問題 P3:
Find $w,\epsilon^n,\epsilon^2,…,\epsilon^N$ that minimize $C$
$$C=\frac{1}{2}\Vert{w}\Vert ^2+\lambda\sum_{n=1}^N \epsilon^n \\ For \forall{y}\neq{\hat{y}^n}: w\cdot (\phi(x^n,\hat{y}^n)-\phi(x^n,y))\leq \triangle (\hat{y}^n,y)-\epsilon^n,\epsilon^n\leq 0$$
注意到,對於一個 n-th training pair $(x^n,\hat{y}^n)$ 和給定一個 $y\neq\hat{y}^n$ 來說,我們都會得到一個 linear constraint。可以將上面式子的 constant 用 a, b來表示變成:
$w\cdot a \leq b - \epsilon^n \\$
發現了嗎? 對於變數 $w$ 和 $\epsilon^n$ 來說,這就是一個 linear constraint。
眼尖的讀者,可能就會覺得 P3 很眼熟。沒錯!它跟 SVM 長很像! 讓我們來跟 SVM 的 Primal form (不是 dual form) 做個比較吧。可以發現有兩點不同,原 SVM from wiki 列出如下: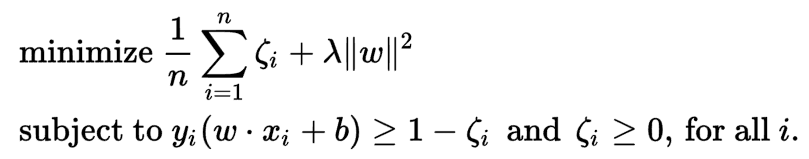
- Margin term 的不同,P3 的 margin 比較 general,可以根據每個 negative case 都有自己的 margin,而原來 binary SVM 的 margin 是定為 1。
- Constraint 個數的不同,原 SVM 個數為 training data 的個數,但是 P3 的個數為無窮多個。
呼! 所以 P3 這個問題,就是 SVM 的 general 版本,我們也稱之為 Structure SVM,這裡終於跟 SVM 連結上了!
Cutting Plane Algorithm
原先 SVM 有限的 constraint 下,我們直接用一個 QP solver可以很快處理掉。但在 Structure SVM 有無窮多的 constraints 究竟要怎麼解? 是個問題。
首先觀察到,其實很多 constraints 都是無效的。例如:
所以這個演算法策略就是從一個空的 working set $\mathbb{A}^n$ 出發,每次 iteration 都找一個最 violate 的 constraint 加進去,直到無法再加入任何的 constraint 為止。
這裡其實有兩個問題要討論,第一個是什麼是最 violate 的 constraint? 第二個是,這演算法會收斂嗎? 難道不會永遠都找得到 violate 的 constraint 一直加入嗎?
我們先把演算法列出來,再來討論上面這兩個問題。
Most Violated Constraint
直接秀李老師的投影片
注意到在 Degree of Violation 的推導中,所有與變數 $y$ 無關的部分可以去掉。因此我們最後可以得到求 Most Violated Constraint 就是在求 Problem 2 ($argmax_y$)。注意到其實我們一直 “先假裝 Problem 2 已解”
Convergence?
論文中證明如果讓 violate 的條件是必須超過一個 threshold 才算 violated,則演算法會在有限步驟內收斂。嚴謹的數學證明要參考 paper。
最後的麻煩: Problem 2 argmax
這篇實在打太長了,以至於我想省略這個地方了 (淚),事實上解 Problem 2 必須看問題本身是什麼,以 POS (Part-Of-Speech) tagging 來說,Problem 2 可用 Viterbi 求解。而這也就是李教授下一個課程 Sequence Labeling Problem。
POS 如何對應到 Structure Learning 實在非常精彩! 真的不得不佩服這些人的智慧! 有興趣的讀者請一定要看李教授的投影片內容!
簡單筆記一下: POS 使用 HMM 方式來 model,例如一句話 x = “John saw the saw” 對應到詞性 y = “PN V D N”。然後把詞性當作 state, word 當作 observation,就是一個典型的 HMM 結構。接著使用 Conditional Random Field (CRF) 將 $log P(x,y)$ 對應到 $w\cdot\phi(x,y)$ 的形式,在 $P(x,y)$ 是由 HMM 定義的情形下,我們可以寫出相對應的 $\phi(x,y)$ 該如何定義。因此就轉成一個 structure learning 的格式了。詳細請參考李老師課程講義。
彩蛋
- 我心愛的晏寶貝三歲生日快樂!
- 這幾天會有一個很重大的決定發生!