2011年自己做的筆記, 放上來以免檔案丟失, 也方便隨時參考. 參考自 “Numerical Optimization” by Jorge Nocedal and Stephen J. Wright. 但是打算只用 Lagrange Multiplier Theorem 理解 KKT. :)
就像是一般微積分裡學到的一樣, 對於一個函式 $f(x)$ 若 $x^\ast$ 為一 minimal/maximum point, 則必要條件為 $f’(x^\ast)=0$. 而在 constraint optimization 版本必要條件變成 KKT conditions. 說更清楚一點就是, 若 $x^\ast$ 為一 minimal/maximum point (+滿足某些神秘條件) , 則必要條件為在 $x^\ast$ 滿足 KKT Conditions.
神秘條件稱為 Constraint Qualifications, 常見的為 LICQ, 在 Convex opt 裡為 Slater’s condition. wiki KKT
具體來說,我們要探討的是對於以下的問題,如果 $x^\ast$ 為一 minimal point 且滿足式 (2) 的條件, 則會發生什麼事情 (我們找的是必要條件)
$$\begin{align} \min f(x) \\ \mbox{subject to } \begin{array}{rcl} c_i(x)=0,i \in \mathbf{E} \\ c_i(x)\geq 0, i \in \mathbf{I} \\ \end{array} \end{align}$$Descent Direction
一般這樣的問題不會有 closed form solution, 因此會使用數值最佳化的方式, 找出一個 sequence $(x_k)$ 來逼近 $x^\ast$. 問題是如何讓這樣的 sequence 逼近一個 (local) minimum? 一個嘗試是至少先讓找到的每一個 $x_k$ 都比前一步更好. 換句話說就是要保證找到的 $x_k$ 滿足
$f(x_k)<f(x_{k-1})$
有了這個想法, 再來就是該怎麼找下一個點, 或是說, 基於現在的點 $x_k$, 該往哪個方向 $d$, 走多遠 $t$? 也因此,我們也就衍生了一個問題, 往哪個方向走函數值會保證下降 (descent direction)?
Descent direction 保證了在該方向上只要不要走太大步, 目標函數值一定會下降, 反過來說, 如果 $x^\ast$ 已經是 (local) minimum 了, 在該點上不應該存在 descent direction. 基於上述的討論, 我們有必要了解清楚 descent direction. 定義如下
[Def]:
令 $f \in C^1(\mathbb{R}^n,\mathbb{R})$, 我們稱 $d$ 為 $x_0$ 的一個 descent direction 如果滿足: $\exists t>0$, such that $f(x_0+sd)<f(x_0),\forall s \leq t$
其實很容易證得: 只要該方向 $d$ 跟 gradient $\triangledown f(x_0)$ 方向相反, 就會是 $x_0$ 的一個 descent direction
[Thm1]:
令 $f \in C^1(\mathbb{R}^n,\mathbb{R})$, 如果滿足 $\triangledown f(x_0)^Td<0$ 則 $d$ 就會是 $x_0$ 的一個 descent direction[Pf]: 由微分的定義出發
$$\lim_{t\rightarrow 0^+}\frac{f(x_0+td)-f(x_0)-\triangledown f(x_0)^Ttd}{\parallel td \parallel}=0 \\ \Rightarrow \lim_{t\rightarrow 0^+}\frac{f(x_0+td)-f(x_0)}{t \parallel d \parallel}=\triangledown f(x_0)^T\frac{d}{\parallel d \parallel} \\ \Rightarrow \lim_{t\rightarrow 0^+}\frac{f(x_0+td)-f(x_0)}{t}=\triangledown f(x_0)^Td<0 \\ \Rightarrow \exists t>0,s.t.,f(x_0+sd)-f(x_0)<0,for\forall s \leq t \\ \Rightarrow \exists t>0,s.t.,f(x_0+sd)<f(x_0),for\forall s \leq t$$
很明顯 steepest descent $d=-\triangledown f(x_0)$ 是 descent direction. 其實只要滿足這種形式 $d=-B\triangledown f(x_0)$ 當 $B$ 是正定,就會是 descent direction. 而當 B 定義為 $\triangledown ^2 f(x_0)$ (Hessian Matrix 是半正定, 通常是 full rank 就會正定), 這種形式就是牛頓法 $d=−\triangledown ^2 f(x_0)\triangledown f (x_0)$
不過我們今天要處理的是 constrained opt, 會有等式或不等式的條件, 因此我們的搜尋空間只能在滿足這些條件下去搜尋, 稱該空間為 feasible set = {x|x滿足所有(2)式的條件}. 可以想像, 在 feasible set 的限制下, 能搜尋的 direction 會被限制. 因此 “Numerical Optimization” 這本書就展開了一系列的討論和證明, 可以得到在這個 feasible set 下, 這些 能搜尋的方向(我們稱為 limiting direction)所構成的集合 究竟長什麼樣. 且發生在最佳解上的 limiting directions 都不會是 descent direction (合理, 不然就找到更佳的解了).
此外, 看課本的話, 會繞更大一圈才會知道什麼是 KKT Conditions (但是相當嚴謹且豐富). 為了清楚了解 KKT, 我們繞過課本的方法, 完全採用微積分學過的 Lagrange Multiplier Theorem 來說明.
了解 KKT Conditions
限制條件為等式
其實 KKT 的表達全部圍繞在 Lagrange Multiplier Theorem 上. 一般課本上講的都是等式條件, 我們列出高維課本裏頭的定理:
不想打 Latex 了 ><, 貼圖好了
[Thm2]: Lagrange Multiplier Theorem
考慮以下問題
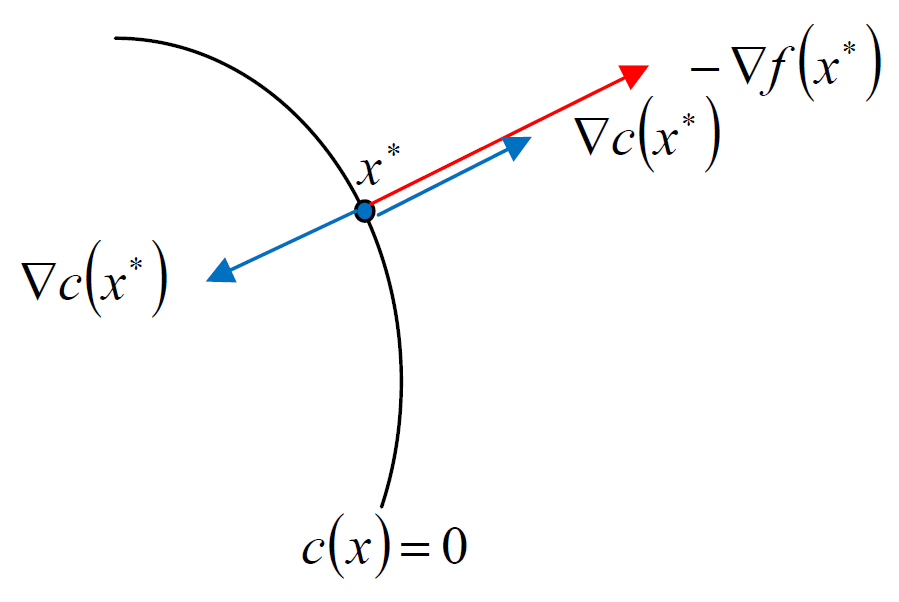
$$\min f(x) \\ \mbox{subject to } \begin{array}{rcl} c(x)=0 \\ \end{array}$$我們可以得到, 若 $x^\ast$ 為一個 local minimum, 由 Thm2 知道, 滿足 $\triangledown f(x^\ast)=\lambda\triangledown c(x^\ast)$, for some $\lambda$
此時的 $\lambda$ 正負都有可能, 也就說明了兩個 gradients 是平行的. 用圖來說明如下:
限制條件為不等式
考慮以下問題
$$\min f(x) \\ \mbox{subject to } \begin{array}{rcl} c(x)\geq 0 \\ \end{array}$$當 $x^\ast$ 為一個 local minimum 會發生什麼事? 分成兩種情況討論:
- $c(x^\ast)=0$
- $c(x^\ast)>0$
第一種情況就退化成條件為等式的情形. 因此存在 $\lambda$ 滿足 $\triangledown f(x^\ast)=\lambda\triangledown c(x^\ast)$. 如果 $\lambda<0$, 導致 $\triangledown c(x^\ast)$ 跟 $\triangledown f(x^\ast)$ 反方向的話, $\triangledown c(x^\ast)^T\triangledown f(x^\ast)<0$ 導致 $\triangledown c(x^\ast)$ 變成一個 desent direction.
則表示我們可以找到一個方向使得目標函數值下降且同時讓條件函數值上升(因此仍然是 feasible), 那麼與 $x^\ast$ 是 local minimum 矛盾.
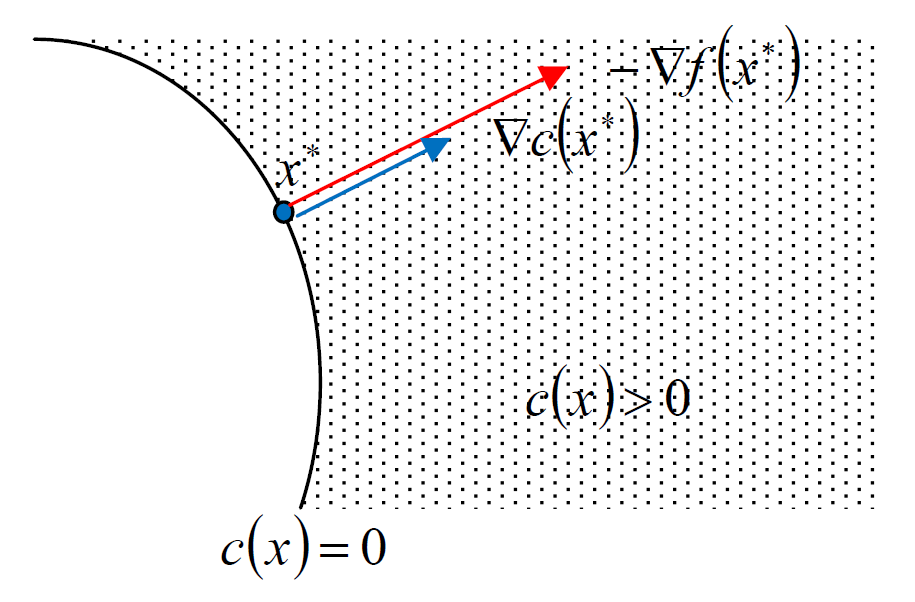
因此得到的結論是 $\triangledown c(x^\ast)$ 跟 $\triangledown f(x^\ast)$ 同方向, i.e., $\lambda\geq 0$. 圖示如下: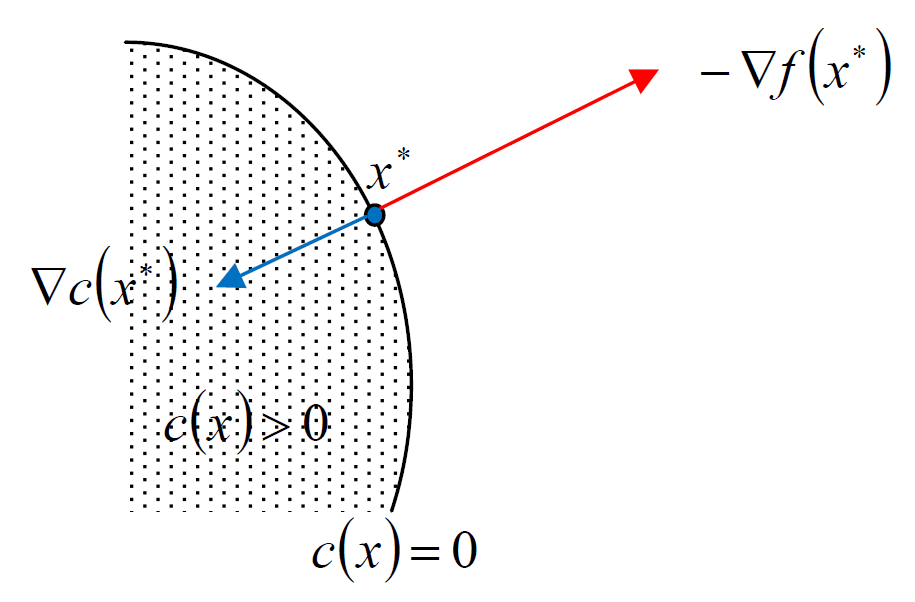
第二種情況是退化成 unconstrained opt, 因為 $x^\ast$ 是在 feasible set 內, 換句話說 $x^\ast$ 是 feasible set 的 interior point. 既然是 unconstrained opt, 且 $x^\ast$ 為 local minimum, 則表示 $\triangledown f(x^\ast)=0$, 所以當然也可以寫成 $\triangledown f(x^\ast)=\lambda\triangledown c(x^\ast)$ 只不過此時的 $\lambda=0$
所以不管是第一種或是第二種情形, 我們都可以寫成
存在 $\lambda\geq 0$ 滿足 $\triangledown f(x^\ast)=\lambda\triangledown c(x^\ast)$
KKT Conditions
到這裡為止, 我們基本上已經可以列出 KKT 了:
[Thm3]: Karush‐Kuhn‐Tucker conditions
[Pf]:
Condition 1 只是說明具有 Lagrange Multiplier 的表達方式: $\triangledown f(x^\ast)=\sum_i{\lambda_i\triangledown c_i(x^\ast)}$
Condition 2,3 是說明 $x^\ast$ 是 feasible point, 這是廢話
Condition 4 說明 若條件為不等式, 相對應的 Lagrange Multipliers 必須大於等於0, 我們在上一段討論了
Condition 5 稱為 complementarity slackness (我知道很難念…), 這需要稍微說明一下
如果 $c_i$ 是等式條件, 則 $c_i(x^\ast)=0$, 因此滿足 Condition 5
如果 $c_i$ 是不等式條件, 但是 $c_i(x^\ast)=0$, 同樣也滿足 Condition 5
最後一種情況是 $c_i$ 是不等式條件, 且 $c_i(x^\ast)>0$. 還記得我們上面針對此種情形的討論嗎? 我們會令他的 $\lambda_i=0$, 所以還是滿足 Condition 5.
這裡沒有提到一件事情就是 LICQ, 全名 Linear Independent Constraint Qualification, 可參考 wiki KKT. LICQ 條件為: 對於某一點 feasible point x, 所有等式條件 (包含那些不等式條件但剛好在 x 變成等式) 在 x 這點的 gradients 都是線性獨立. 這個條件正好可以從 [Thm2]: Lagrange Multiplier Theorem 裡面看出來, Thm2 說明如果等式條件的 gradients 都線性獨立, 可以把 $\mu=1$, 因此可以寫成 Condition 1: $\triangledown f(x^\ast)=\sum_i{\lambda_i\triangledown c_i(x^\ast)}$, 也因此可以滿足 KKT.
課本裡的證法
課本裡的證明實在頗迂迴, 但是提供了很豐富和深刻的理解. 這裡還是努力記錄下來吧! {數學多, 謹慎服用}
我們分成5個步驟來討論:
- Limiting directions
- Limiting direction 與 Local minimum 的關聯
- Limiting directions 的集合, 就稱為 F 吧
- LICQ 成立時, “Limiting directions 都不是 descent direction” 與 “Lagrange Multipliers” 的等價關係
- 串起來變成 KKT
1. Limiting directions
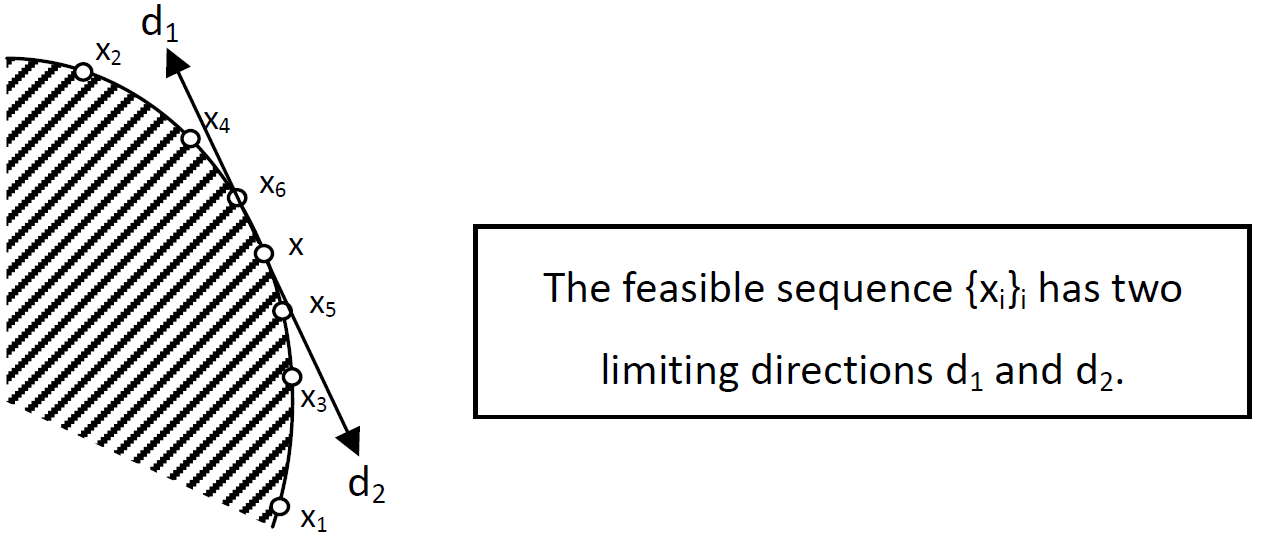
直觀來說, 對於某一點 $x_0$ (當然屬於 feasible set) 用在 feasible set 中的某條路徑去逼近它, 而逼近的最後方向就是 limiting direction. 另外, 一個 sequence ${z_k}$ 都屬於 feasible set , 都不等於 $x_0$, 且最後逼近 $x_0$, 我們稱為 feasible sequence.
[Def]:
若滿足以下條件稱 $d$ 是 $x_0$ 的 limiting direction. (當然 $x_0$ 是 feasible point)
存在一個 feasible sequence $(z_k)_k$ 使得該 sequence 有一個 subsequence
$$\exists (z_{k_j})_j \mbox{ such that } d = \lim\frac{(z_{k_j}-x_0)}{\parallel z_{k_j}-x_0\parallel}$$
從定義上我們可以知道 limiting direction 長度為 1, 因為我們只在乎方向. 另外要特別說存在一個 subsequence 是因為 feasible sequence 不會只有一個 limiting direction. 例子如下:
2. Limiting direction 與 Local minimum 的關聯
文章開頭有說明, “如果 $x^\ast$ 已經是 (local) minimum 了, 在該點上不應該存在 descent direction.” 對於 constrained opt 的版本相當於 “如果 $x^\ast$ 已經是 (local) minimum 了, 它的 limiting directions 都不能是 descent direction.” 用數學寫出來如下:
[Thm4]:
已知 $x^\ast$ 是一個 local minimum, 則它所有的 limiting direction $d$ 都滿足 $\triangledown f(x^\ast)^Td \geq 0$
直觀上如果不滿足, 我們就可以找到一個 feasible sequence 從而得到該 limiting direction 會是一個 descent direction, 因此與 $x^\ast$ 是 local minium 矛盾.
我們在等下的第4個步驟可以看到此條件 “所有的 limiting direction $d$ 都滿足 $\triangledown f(x^\ast)^Td \geq 0$” 等價於 KKT Conditions 的表達方式. 因此 Thm4 可以重寫成 “已知 $x^\ast$ 是一個 local minimum, 則滿足 KKT Conditions”, 在最後第5步會串起來.
3. Limiting directions 的集合 (F)
[Def]: Active Set
對於某一 feasible point $x_0$, 它的 active set $\mathbf{A}(x_0)$ 定義為
$\mathbf{A}(x_0) = \mathbf{E} \cup \{i \in \mathbf{I} | c_i(x_0)=0 \}$[Def]: LICQ
如果以下集合為線性獨立集, 則稱 LICQ 在 $x_0$ 成立
$\{\triangledown c_i(x_0), i \in \mathbf{A}(x_0) \}$
其實我們在上面的討論都有使用這兩個定義, 這裡只不過用數學表示方便等下的討論.
某一點它的所有 limiting direction 的集合 ($F$) 如下:
[Thm5]:
對於某一 feasible point $x_0$,
$$F=\left\{ \begin{array}{c|r} d & \begin{array}{rcl} d^T\triangledown c_i(x_0)=0,i \in \mathbf{E} \\ d^T\triangledown c_i(x_0) \geq 0, i \in \mathbf{A}(x_0) \cap \mathbf{I} \\ \parallel d \parallel = 1\\ \end{array} \end{array} \right\}$$
為了不模糊焦點, 證明就跳過, 想看的童鞋門就查一下舊的筆記
另外, 定義 $F_1=\alpha F$, for $\alpha\geq 0$ (所以是 convex cone). 因此 $F1$ 只不過是把 $\parallel d \parallel =1$ 的條件去調.
4. LICQ 成立時, 關鍵的等價關係
我們以下都假設 LICQ 成立, 這麼做就可以很方便地讓 limiting direction 的集合用 $F1$ 來表示.
還記得在 “2. Limiting direction 與 Local minimum 的關聯” 有提到我們希望找到某一 feasible point $x_0$ 的 $F1$ 都不是 descent direction, 因此該點就很有可能是我要找的 local optimum.
而這一個條件 “某一 feasible point $x_0$ 的 $F1$ 都不是 descent direction” 其實與 Lagrange Multipliers 息息相關, 也因此跟 KKT conditions 會產生連結. 下面定理可以證明這個條件可以等價於 KKT condition 的表達方式.
[Thm6]:
對於某一 feasible point $x_0$, Let $\mathbf{A}(x_0)=(1…m)$, $\mathbf{A}^T=[\triangledown c_1(x_0)…\triangledown c_m(x_0)]$ 則
$$\triangledown f(x-0)^Td\geq 0,\forall d \in F1 \Leftrightarrow\\ \exists \lambda \in \mathbb{R}^m \mbox{ where } \lambda_i \geq 0 \forall i \in \mathbf{A}(x_0) \cap \mathbf{I} \mbox{, such that } \triangledown f(x_0)=\sum_{i=1}^m \lambda_i \triangledown c_i(x_0)=\mathbf{A}^T$$
同樣跳過, 證明可查看舊的筆記
我們可以仔細對照一下上面的 Lagrange Multiplier 那個條件, 其實它跟 “[Thm3]: Karush‐Kuhn‐Tucker conditions” 是一樣的, 只差在一個地方就是 complementarity slackness 沒有明確寫出來, 但我們知道一定存在 $\lambda$ 可以滿足. 因此這個 Lagrange Multiplier 的條件也就是 KKT 的表達方式.
5. 串起來變成 KKT
腦袋差不多都打結了, 目前為止到底得到了什麼關係? 我們來整理一下
Thm4 告訴我們一個最佳解一定會使得它的 limiting directions 都不是 descent direction.
Thm5 告訴我們 limiting directions 的集合其實就是 $F1$ (or $F$).
Thm6 告訴我們對於任一個 $F1$ 的 direction, 都不是 descent direction, 等同於滿足 KKT 的表達方式.
將 Thm4,5,6 串起來變成: 一個最佳解滿足 KKT 的表達方式. (當然前提是有滿足 LICQ)
打這篇累到不想有結論的結論
不想有結論了, 乾脆來碎碎念吧. 最佳化是我唸書期間很愛的一門科目, 當時愈是唸它, 愈是不懂. 以前也很愛看 Stephen P. Boyd 的 convex opt 課程, 但現在腦袋裡似乎只剩教授名字和課程名字了. 喔對了, 我還記得一件事情, 就是在 convex 問題時, KKT condition 會變成 充要條件. 至於細節, 恩…
[待補充]: 我有找到當時的筆記關於 convex 問題下的 KKT conditions, 以及它的 dual problem 討論. 只能說: 1. 學生可以很自由掌控自己的時間, 工作後的時間都是零碎的阿! 根本沒法長時間死嗑某一樣學科! 2. 當碼農工程師數學真的會退步, 碼農友碼農的好, 但希望自己也別忘記重要的數學觀念了.
Reference
- Numerical Optimization 2nd edition, Jorge Nocedal
- 筆記 for the proof of Thm5,6


