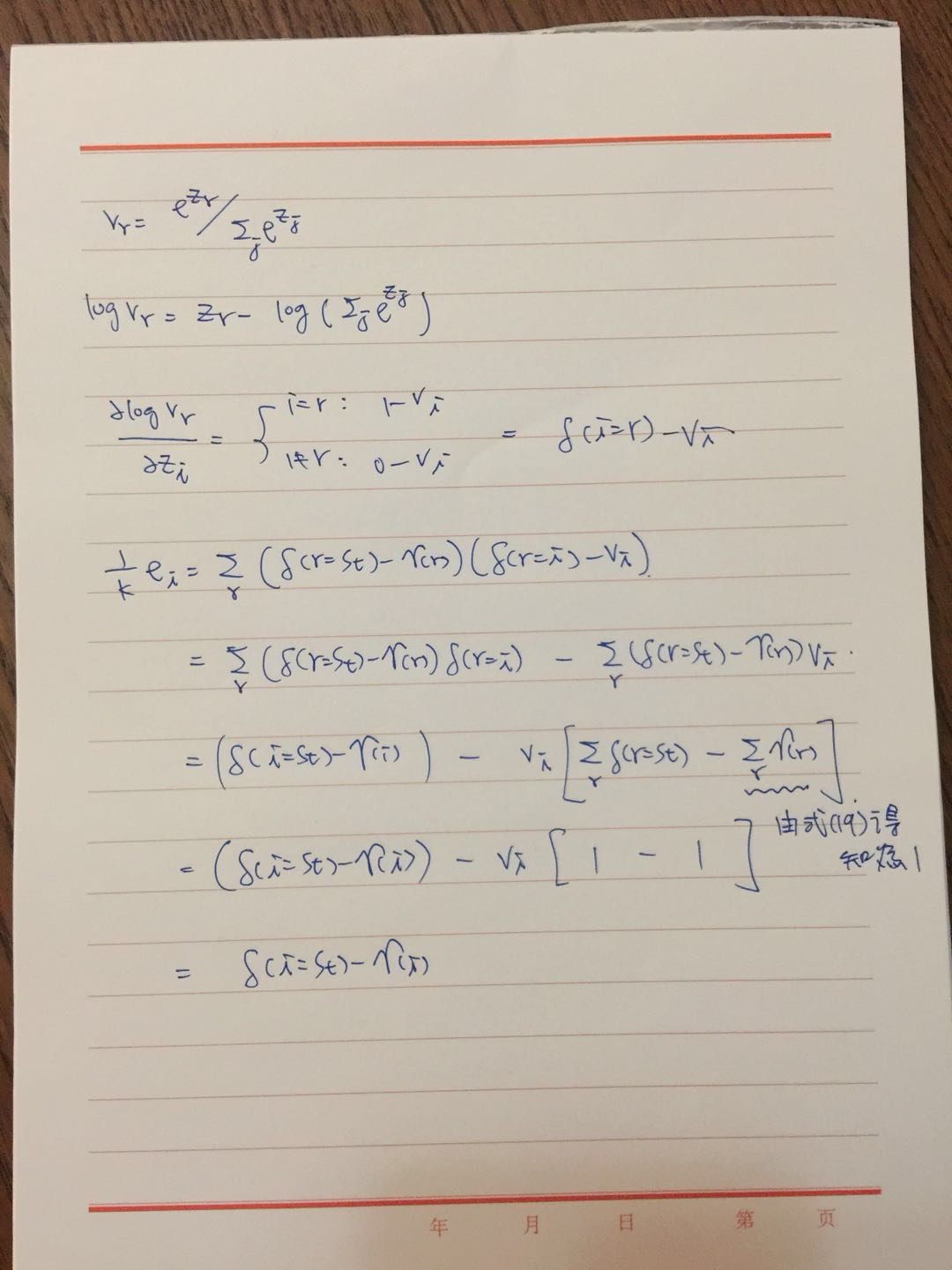Maximum Mutual Information (MMI) 序列的鑑別性訓練方法從早期的 GMM-HMM, 到現今就算使用了深度學習同樣十分有用, 如 Kaldi chain model 在 DNN-HMM 的基礎上加上序列鑑別訓練, 性能會再進一步提升. 前一陣子讀了俞棟、鄧力的這本 語音識別實踐, 對我來說整理得滿好的, 就是數學部分的推導有點簡潔了些, 所以這篇就基於該書的推導, 補齊了較詳細的步驟, 並且嘗試使用 Computational graph 的方式理解 MMI 的訓練. 那麼就開始吧!
用自己畫的 MMI 的計算圖譜當封面吧 :)
MMI 數學定義
定義
$o^m=o_1^m,...,o_t^m,...,o_{T_m}^m$
是訓練樣本裡第 m 句話的 observation (MFCC,fbank,…) sequence, 該 sequence 有 $T_m$ 個 observation vector. 而
$w^m=w_1^m,...,w_t^m,...,w_{N_m}^m$
則是該句話的正確 transcription, 有 $N_m$ 個字. 通過 forced-alignment 可以得到相對應的 state sequence
$s^m=s_1^m,...,s_t^m,...,s_{T_m}^m$
MMI 目的就是希望模型算出的正確答案 sequence 機率愈大愈好, 同時非正確答案 (與之競爭的其他 sequences) 的機率要愈小愈好, 所以正確答案放分子, 非正確放分母, 整體要愈大愈好. 由於考慮了競爭 sequences 的最小化, 所以是鑑別性訓練. 又此種方始是基於整句的 sequence 考量, 因此是序列鑑別性訓練. 數學寫下來如下:
$$J_{MMI}(\theta;S)=\sum_{m=1}^M J_{MMI}(\theta\|o^m,w^m) \\
=\sum_{m=1}^M \log \frac{ p(o^m\|s^m,\theta)^KP(w^m) }{ \sum_w p(o^m\|s^w,\theta)^K P(w) }$$
為了簡單化, 我們假設只有一條訓練語音, 所以去掉 $m$ 的標記, 然後 $\sum_m$ 省略:
$$\begin{align} J_{MMI}(\theta\|o,w) =\log \frac{ p(o\|s,\theta)^KP(w) }{ \sum_w p(o\|s^w,\theta)^K P(w) } \end{align}$$接著我們要算針對 $\theta$ 的微分, 才可以使用梯度下降算法:
$$\begin{align} \triangledown_\theta J_{MMI}(\theta\|o,w) =\sum_t \triangledown_{z_t^L}J_{MMI}(\theta\|o,w)\frac{\partial z_t^L}{\partial\theta} \\ =\sum_t e_t^L\frac{\partial z_t^L}{\partial\theta} \end{align}$$其中定義
$e_t^L=\triangledown_{z_t^L}J_{MMI}(\theta\|o,w)$
語音聲學模型 (AM) 傳統上使用 GMM 來 model, 而現在都是基於 DNN, 其中最後的 output layer 假設為第 $L$ 層: $z_t^L$, 過了 softmax 之後我們定義為 $v_t^L$, 而其 index $r$, $v_t^L(r)=P(r|o_t)$ 就是給定某一個時間 $t$ 的 observation $o_t$ 是 state $r$ 的機率.
讀者別緊張, 我們用 Computational graph 的方式將上式直接畫出來:
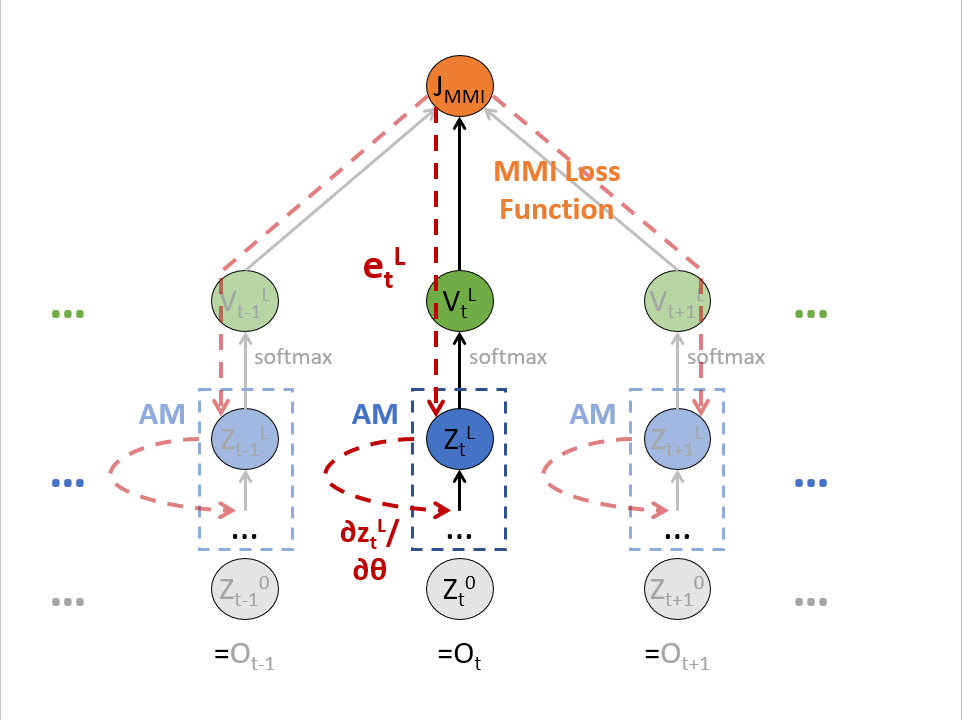
MMI Computational Graph 表達
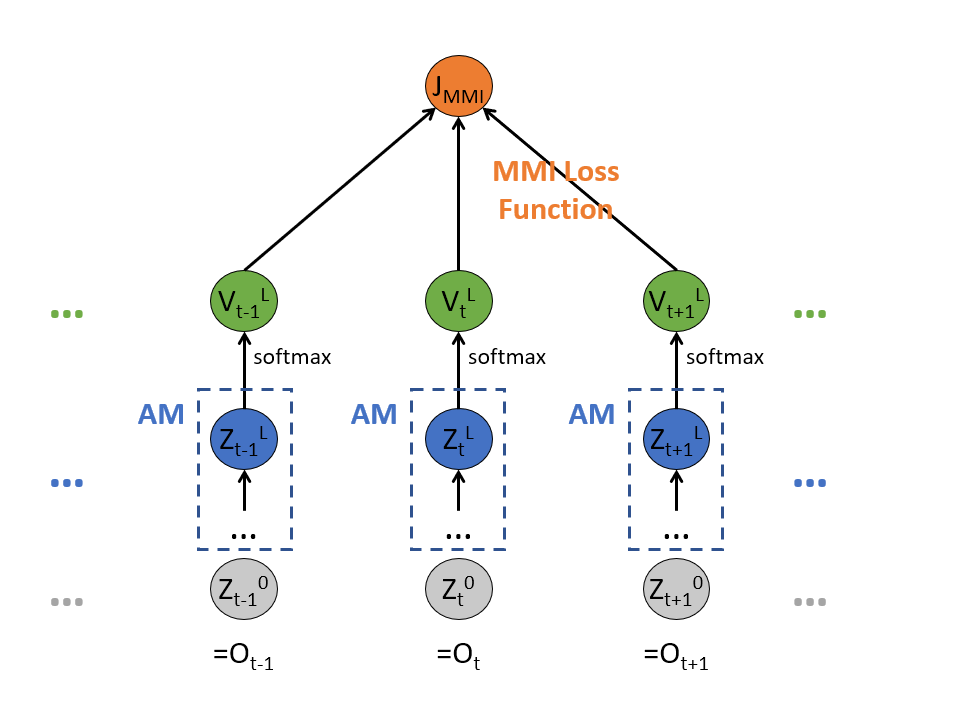

上圖用 computational graph 清楚的表達了式 (3) 的計算, 因為所有參數 $\theta$ 在所有的時間 $t$ 上是共享的, 因此要 $\sum_t$, 也就是要累加上圖所有紅色的 gradient path.
計算 $\partial z_t^L / \partial\theta$ 很容易, 就是 DNN 的計算圖譜的 gradient, 因此重點就在如何計算 $e_t^L$, 而整個 MMI 最核心的地方就是在計算這個了!
MMI 數學推導
我們把 $e_t^L(i)$ (就是$e_t^L$這個向量的第$i$個element)計算如下:
$$\begin{align} e_t^L(i)=\triangledown_{z_t^L(i)}J_{MMI}(\theta\|o,w) \\ =\sum_r \frac{\partial J_{MMI}(\theta\|o,w)}{\partial\log p(o_t|r)}\frac{\partial\log p(o_t|r)}{\partial z_t^L(i)} \end{align}$$先解釋一下 $\log p(o_t|r)$ 這個 term, 可以重寫成
$$\begin{align}
\log p(o_t|r)=\log \color{red}{p(r|o_t)} + \log p(o_t) - \log p(r) = \log \color{red}{v_t^L(r)} + \log p(o_t) - \log p(r)
\end{align}$$
所以這個 term 是跟 $v_t^L(r)$ 相關的, 而由於 $v_t^L$ 是 $z_t^L$ 經過 softmax 得到, 因此式(5)才會有 $\sum_r$.
根據式 (6), 我們可以很快算得式 (5) 的第二個分子分母項如下:
$$\begin{align}
\frac{\partial\left[\log v_t^L(r) + \log p(o_t) - \log p(r)\right]}{\partial z_t^L(i)}=\frac{\partial \log v_t^L(r)}{\partial z_t^L(i)}
\end{align}$$
很明顯因為 $\log p(o_t)$ 和 $\log p(r)$ 都跟 $z_t^L(i)$ 無關所以去掉.
為了計算式 (5) 的第一個分子分母項, 我們把先把式 (1) 的 log 項拆開:
$$\begin{align}
J_{MMI}(\theta\|o,w)=
K\color{green}{\log p(o\|s,\theta)}+\color{blue}{\log p(w)} - \color{orange}{\log\left[\sum_w p(o\|s^w,\theta)^K p(w)\right]}
\end{align}$$
所以
$$\begin{align}
\frac{\partial J_{MMI}(\theta\|o,w)}{\partial \log p(o_t|r)}=
K\color{green}{
\frac{\partial\log p(o\|s,\theta)}{\partial \log p(o_t|r)}
}
+
\color{blue}{
\frac{\partial\log p(w)}{\partial \log p(o_t|r)}
}
-
\color{orange}{
\frac{\partial\log\left[\sum_w p(o\|s^w,\theta)^K p(w)\right]}{\partial \log p(o_t|r)}
}
\end{align}$$
綠色部分
注意到 $\log p(o|s,\theta)$ 在 HMM 的情況下, 是給定 state sequence 的觀測機率值, 因此只是每個 state 時間點的 emission probability, 所以
$$\begin{align}
\log p(o\|s,\theta)=
\sum_{t'} \log p(o_{t'}\|s_{t'},\theta)
\end{align}$$
而只有 $t’=t$ 時與微分項有關, 因此變成
$$\begin{align}
\frac{\partial\log p(o\|s,\theta)}{\partial \log p(o_t\|r)}=
\frac{\partial \log p(o_t\|s_t,\theta)}{\partial \log p(o_t\|r)}=\delta(r=s_t)
\end{align}$$
藍色部分
與微分項無關,因此
$$\begin{align}
\frac{\partial\log p(w)}{\partial \log p(o_t|r)}=0
\end{align}$$
橘色部分
$$\begin{align} \frac{\partial\log\left[\sum_w p(o\|s^w,\theta)^K p(w)\right]}{\partial \log p(o_t|r)}= \frac{1}{\sum_w p(o\|s^w,\theta)^K p(w)}\times\frac{\partial \sum_w \color{red}{p(o\|s^w,\theta)}^K p(w)}{\partial \log p(o_t|r)} \end{align}$$紅色的部分如同上面綠色項的討論, 只有時間點 $t$ 才跟微分項有關, 不同的是這次沒有 $\log$ 因此是連乘, 如果 $s_t\neq r$ 整條 sequence 的機率與微分項無關, 因此只會保留 $s_t=r$ 的那些 $w$ sequences.
另外,
$\frac{\partial p(o_t\|r)^K}{\partial\log p(o_t\|r)} \mbox{ 可想成 } \frac{\partial e^{Kx}}{\partial x} = Ke^{Kx}$
綜合以上討論橘色部分為
$$\begin{align}
\frac{\partial\log\left[\sum_w p(o\|s^w,\theta)^K p(w)\right]}{\partial \log p(o_t|r)}=
K\frac{\sum_{w:s_t=r}p(o\|s,\theta)^K p(w)}{\sum_w p(o\|s^w,\theta)^K p(w)}
\end{align}$$
全部帶入並整理 $e_t^L(i)$
將 (11),(12),(14) 代回到 (9) 我們得到
$$\begin{align}
\frac{\partial J_{MMI}(\theta\|o,w)}{\partial \log p(o_t|r)}=
K\left(\delta(r=s_t)-\frac{\sum_{w:s_t=r}p(o\|s,\theta)^K p(w)}{\sum_w p(o\|s^w,\theta)^K p(w)}\right)
\end{align}$$
繼續將 (15),(7) 代回到 (5) 我們終於可以得到 $e_t^L(i)$ 的結果了!
$$\begin{align}
e_t^L(i)=\sum_r K\left(\delta(r=s_t)-\frac{\sum_{w:s_t=r}p(o\|s,\theta)^K p(w)}{\sum_w p(o\|s^w,\theta)^K p(w)}\right) \times \frac{\partial \log v_t^L(r)}{\partial z_t^L(i)} \\
= \sum_r K\left(\delta(r=s_t)-\color{red}{\gamma_t^{DEN}(r)}\right) \times \frac{\partial \log v_t^L(r)}{\partial z_t^L(i)} \\
=K\left(\delta(i=s_t)-\gamma_t^{DEN}(i)\right)
\end{align}$$
其中一個很重要的定義
$$\begin{align}
\gamma_t^{DEN}(r)=\frac{\sum_{w:s_t=r}p(o\|s,\theta)^K p(w)}{\sum_w p(o\|s^w,\theta)^K p(w)}
\end{align}$$
物理意義就是時間$t$在狀態$r$的機率! 理論上來說我們要取遍所有可能的 word sequence $w$ 並求和計算, 但實際上只會在 decoding 時的 lattice 上計算, 以節省時間. 到目前為止我們算完了 MMI 最困難的部分了, 得到 $e_t^L(i)$ 後 (式(18)),剩下的就只是 follow 上圖的 MMI computational graph 去做.
有讀者來信詢問式 (17) 如何推導至 (18), 過程如下圖: (抱歉偷懶不打 Latex 了)
結論
還有一些其他變種如 boost MMI (bMMI)、MPE、MCE等等, 差別只是在最小化不同的標註精細度, 最重要的還是要先了解 MMI 就可以容易推廣了. 這些都有一個統一的表達法如下:
$$\begin{align}
e_t^L(i)=K\left(\gamma_t^{DEN}(i)-\gamma_t^{NUM}(i)\right)
\end{align}$$
注意到正負號跟 (18) 相反, 因為只是一個最大化改成最小化表示而已. 並且多了一個分子的 lattice 計算.