Mixtures of Factor Analyzers

這篇使用 Bishop PRML 的 notations, 同使參考 Zoubin Ghahramani and Geoffrey E. Hinton (沒錯, 就是那位 Hiton, 另外, 第一作者也是神人級別, 劍橋教授, Uber 首席科學家) 1997 年的論文 “The EM Algorithm for Mixtures of Factor Analyzers“, 實作了 Mixtures of Factor Analyzers, 臥槽! 都20年去了! My python implementation, github. 關於 EM 的部分會比較精簡, 想看更多描述推薦直接看 PRML book.

文章主要分三個部分

什麼是 Factor Analysis, 以及它的 EM 解
推廣到 mixtures models
語者識別中很關鍵的 ivector 究竟跟 FA 有什麼關聯?

直接進入正題吧~

Factor Analysis

一言以蔽之, sub-space 降維. 假設我們都活在陰魂不散的 Gauss 世界中, 所有 model 都是高斯分布.

我們觀察的資料 $x$ 都是高斯分布, 且都是高維度. 但實際上 $x$ 通常只由少數幾個看不到的變數控制, 一般稱這些看不到的變數為 latent variable $z$. 如下圖舉例:

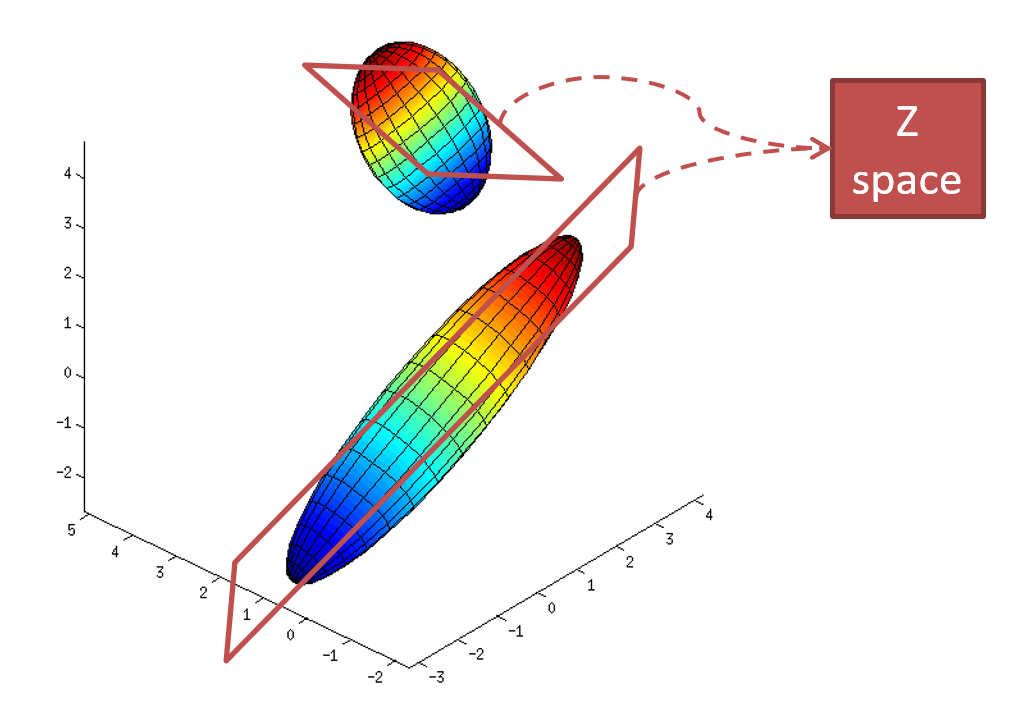
所以我們的主要問題就是, 怎麼對 Gaussian distribution 建立 sub-space 模型? 答案就是使用 Linear Gaussian Model.

一些 notations 定義: $x$ 表示我們的 observation, 維度是 $D$. $z$ 是我們的 latent variable, 維度是 $K$. 我們一般都期望 $K \ll D$. $x$ and $z$ follow linear-Gaussian framework, 有如下的關係:

$$\begin{align} p(z)=N(z|0,I) \\ p(x|z)=N(x|Wz+\mu,\Psi) \\ \end{align}$$

$W$ 是一個線性轉換, 將低維度的 latent space 轉換到高維度的 observation space, 另外 $\Psi$ 必須是對角矩陣. 由於是對角的關係, 因此 $\Psi$ 捕捉了 obaservation 維度的各自變異量, 因此稱為 uniquenesses, 而 $W$ 就是負責捕捉共同項, 稱為 factor loading. 書裡有一個簡單明瞭的圖解釋上述的模型, 我就不多說了, 自行看圖:

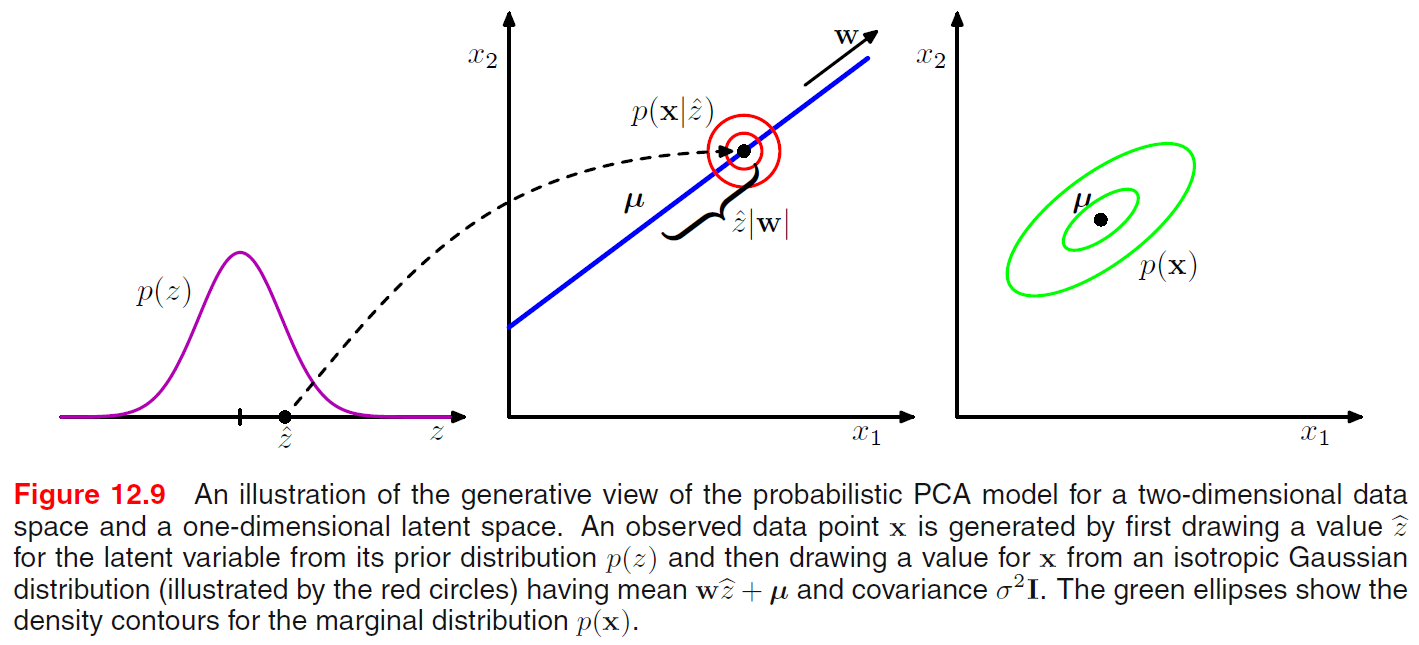
因為是 linear-Gaussian model, 所以 marginal distribution 也是 Gaussian:

$$\begin{align} p(x)=N(x|\mu,C) \\ \mbox{where } C=WW^T+\Psi \end{align}$$

同時, 事後機率也是 Gaussian

$$\begin{align} p(z|x)=N(z|GW^T\Psi^{-1}(x-\bar{x}),G^{-1}) \\ \mbox{where } G=(I+W^T\Psi^{-1}W)^{-1} \end{align}$$

完整的 lineaer-Gaussian model 公式, from PRML book:

有了 $p(x)$ (式 3) 基本上我們就可以根據 training data 算出 likelihood, 然後找出什麼樣的參數可以最大化它. 但是這裡的問題是含有未知變數 $z$, 這個在 training data 看不到, 因為我們只看的到 $x$.

不過別擔心, EM 演算法可以處理含有未知變數情況下的 maximal likelihood estimation. 忘了什麼是 EM, 可以參考一下這. 很精簡的講一下就是, 找到一個輔助函數 $Q$, 該輔助函數一定小於原來的 likelihood 函數, 因此只要找到一組參數可以對輔助函數最大化, 那麼對於原來的 likelihood 函數也會有提升, 重複下去就可以持續提升, 直到 local maximum.
另外輔助函數就是 “complete-data log likelihood and take its expectation with respect to the posterior distribution of the latent distribution evaluated using ‘old’ parameter values”, 我知道很粗略, 還請自行看筆記或是 PRML Ch9.

E-Step

E-Step 主要算出基於舊參數下的事後機率的一階二階統計量

首先將符號做簡化, 方便後面的式子更簡潔 ($n$ 是訓練資料的 index):

$$\mathbb{E}[z_n]\equiv\mathbb{E}_{z_n|x_n}[z_n] \\ \mathbb{E}[z_nz_n^T]\equiv\mathbb{E}_{z_n|x_n}[z_nz_n^T] \\$$

事後機率的一階二階統計量如下:

$$\begin{align} \mathbb{E}[z_n] = GW^T\Psi^{-1}(x_n-\mu) \\ \mathbb{E}[z_nz_n^T] = G + \mathbb{E}[z_n] \mathbb{E}[z_n]^T \\ \mbox{where } G=(I+W^T\Psi^{-1}W)^{-1} \end{align}$$

因為事後機率是 Gaussian, 所以由式 (5) 可以推得式 (7) 和式 (8).

M-Step

這一步就是最大化輔助函數 $Q$, 其中 $\mu$ 等於 sample mean, 可以直接寫死不需要 iteration. 另外兩個參數 update 如下:

$$\begin{align} W^{new}=\left[\sum_{n=1}^N (x_n-\mu)\mathbb{E}[z_n]^T\right]\left[\sum_{n=1}^N \mathbb{E}[z_nz_n^T]\right]^{-1} \\ \Psi^{new}=\mbox{diag}\left[S-W^{new}\frac{1}{N}\sum_{n=1}^N \mathbb{E}[z_n](x_n-\mu)^T\right] \end{align}$$

$S$ 是 sample covariance matrix (除 N 的那個 biased)

Toy Example

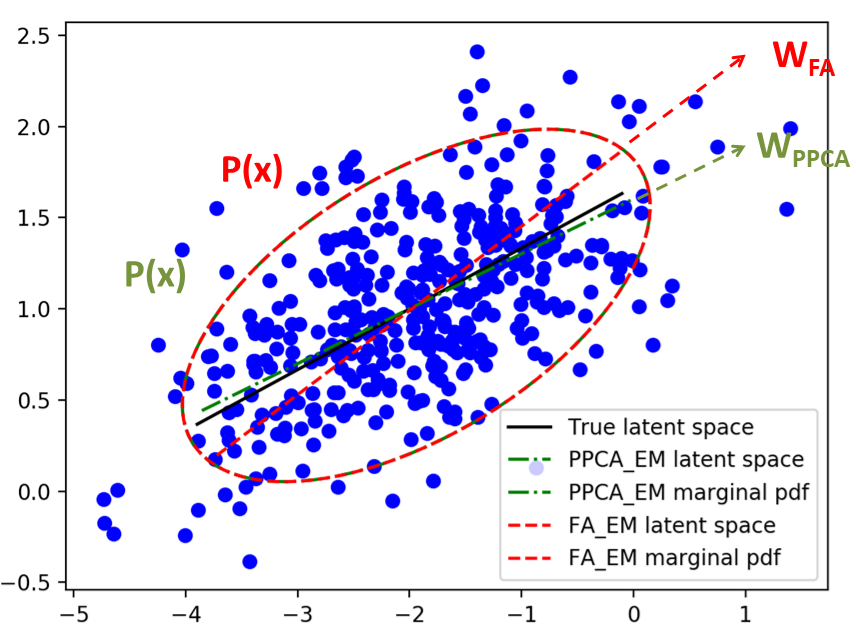
黑色那條線是真正產生資料時的 $W$, 可以當成正確答案. 紅色的是 FA 估計出來的 $W$ 和 $p(x)$. 可以發現 $W$ 沒有跟正確答案一樣, 這是因為我們在做 maximum likelihood 的時候, 只關心 $p(x)$, 因此可以有不同的 latent space 產生相同的 $p(x)$. 範例也一併把 probabilistic PCA 做出來了, 可以發現 PPCA 算的 $W$ 跟正確答案很接近, 這是因為此範例的資料其實是根據 PPCA 的模型產生的, 所以 PPCA 較接近是正常. 同時我們看到 PPCA 估計出來的 $p(x)$ 其實也跟 FA 一樣, 再度佐證 FA 其實也沒算錯, 只是不同的表達方式.

Mixtures of Factor Analyzers

將 FA 假設有多個 components 組成就變成 MFA 了, 其實就跟 GMM 一樣, 差別在於我們用了 latent space 去各別 model 每個 Gaussian Components 而已!

要注意的是, 這時候的 latent variables 不只有 $z$, 還有 $m$ (=1~M 表示有 $M$ 個 components), 我們用下標 $j$ 表示 component 的 index.

另外, 每一個 component, 會有各自的 latent space, 因此有各自的 $W_j$ 和 $\mu_j$, 但是全部的 components 共用一個 uniquenesses $\Psi$.

$$\begin{align} p(x|z,m=j)=N(x|W_j z+\mu_j,\Psi) \end{align}$$

和 GMM 一樣, 每一個 component 都有一個 weights, $\pi_j$, 合起來機率是1

E-Step

一階和二階統計量如下:

$$\begin{align} \color{red}{\mathbb{E}[z_n|m=j]} = G_j W_j^T \Psi^{-1}(x_n-\mu_j) \\ \color{red}{\mathbb{E}[z_nz_n^T|m=j]} = G_j + \mathbb{E}[z_n|m=j] \mathbb{E}[z_n|m=j]^T \\ \mbox{where } G_j=(I+W_j^T\Psi^{-1}W_j)^{-1} \end{align}$$

而真正的事後機率為:

$$\begin{align} \mathbb{E}[m=j,z_n] = h_{nj}\mathbb{E}[z_n|m=j] \\ \mathbb{E}[m=j,z_nz_n^T] = h_{nj}\mathbb{E}[z_nz_n^T|m=j] \\ \mbox{where } \color{red}{h_{nj}}=\mathbb{E}[m=j|x_n]\propto p(x_n,m=j) \end{align}$$

將 (18) 解釋清楚一下, 基本上就是計算給定一個 $x_n$, 它是由 component $j$ 所產生的機率是多少. 我們可以進一步推導如下:

$$\begin{align} p(x_n,m=j)=p(m=j)p(x_n)\\ =\pi_j N(x_n|\mu_j,C_j=W_jW_j^T+\Psi) \end{align}$$

(19) 到 (20) 的部分可以由 (3) 和 (4) 所知道的 marginal distribution $p(x)$ 得到

到這裡, 所有需要的統計量, 紅色部分, 我們都可以算得了.

M-Step

通通微分等於零, 通通微分等於零, 通通微分等於零 … 得到:

$$\begin{align} \pi_j^{new}=\frac{1}{N}\sum_{n=1}^N h_{nj} \\ \mu_j^{new}=\frac{\sum_{n=1}^N h_{nj}x_n}{\sum_{n=1}^N h_{nj}} \\ W_j^{new}=\left[\sum_{n=1}^N h_{nj}(x_n-\mu_j)\mathbb{E}[z_n|m=j]^T\right]\left[\sum_{n=1}^N h_{nj}\mathbb{E}[z_nz_n^T|m=j]\right]^{-1} \\ \Psi^{new}=\frac{1}{N}\mbox{diag}\left[ \sum_{nj} h_{nj} \left( (x_n-\mu_j) - W_j^{new}\mathbb{E}[z_n|m=j] \right)(x_n-\mu_j)^T \right] \end{align}$$

Toy Example

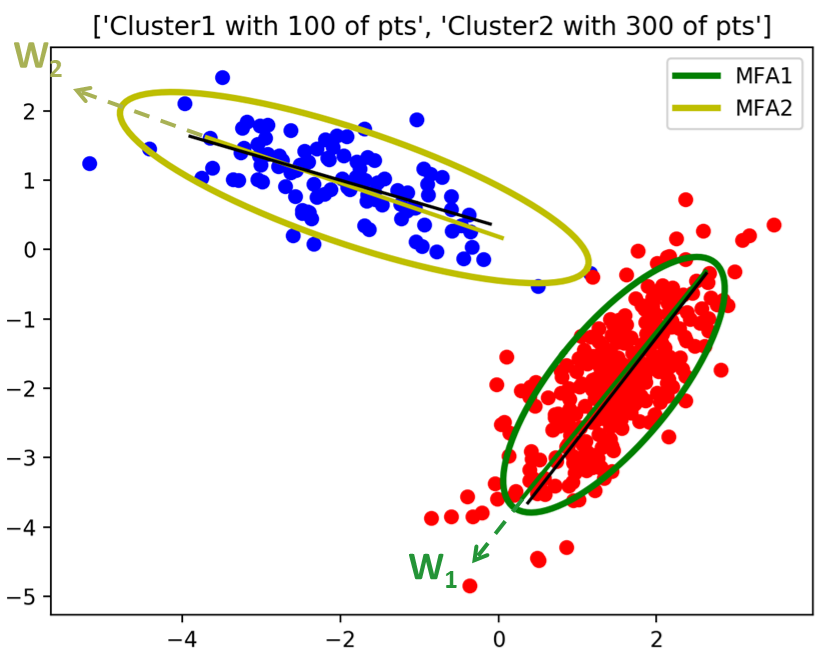
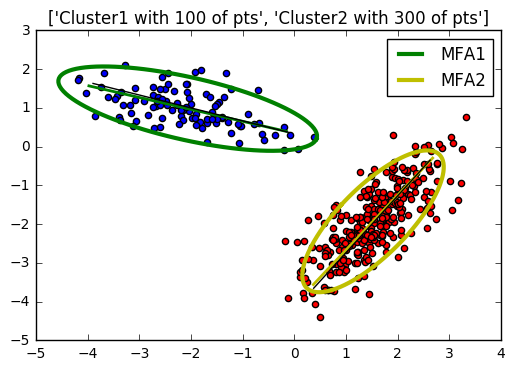
圖應該很清楚了, 有正確 model 到 data

這個 MFA 還真的不容易實作, 寫起來很多要注意的地方, 很燒腦阿! 不過做完了之後頗有成就感~

i-vector

其實會想寫這篇主要是因為語者識別中的 ivector, 而 ivector 基本上就是一個 FA. 在計算 ivector 時, 我們會先估計 Universal Background Model (UBM), 其實就是所有語者的所有語音特徵算出來的 GMM. 以下圖為例, UBM 有三個 mixtures, 用淡藍色表示. 而針對某一位 speaker, 其 GMM 為橘色.

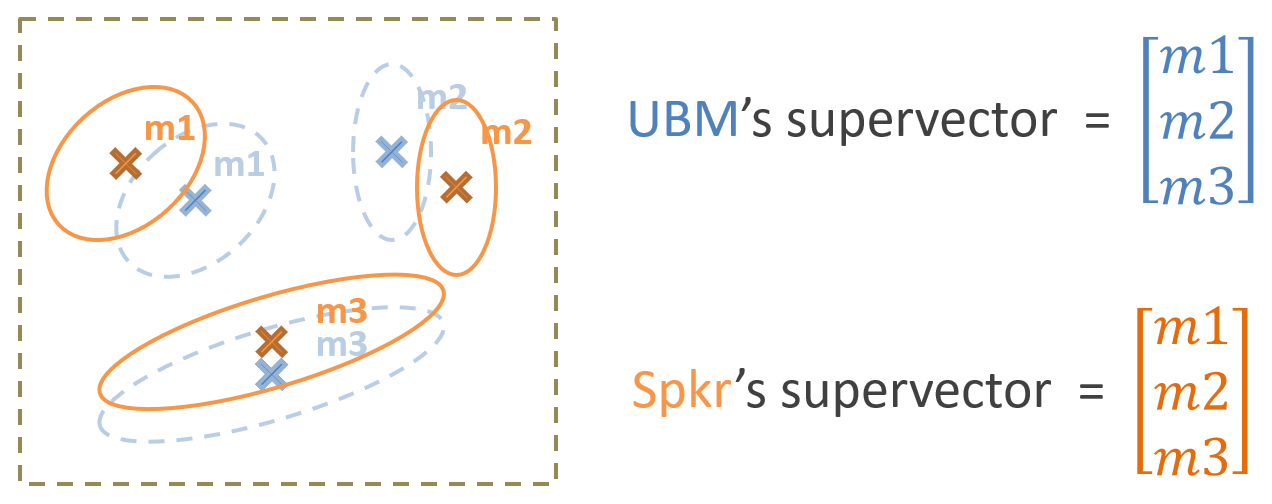
傳統上我們將所有 mixture 的 mean 串接成一個長的向量, 則該向量就可以當作是該 GMM 模型的一個代表, 並稱為 supervector

不一起串接 covariance matrix 嗎? weight 呢? 當然也可以全部都串成一個非常長的向量, 但研究表明 mean 向量就足夠了

supervector 維度為 mfcc-dim x mixture數, 很容易有 40x1024 這麼高維! 因此 ivector 就是利用 FA 的方法將 supervector 降維. 那具體怎麼做呢? 首先我們要先用一個小技巧將 “多個 Gaussians” (注意不是 GMM, 因為沒有mixture weight的概念, 每一個 Gaussian都同等重要) 轉換成一個 Gaussain. 見圖如下:

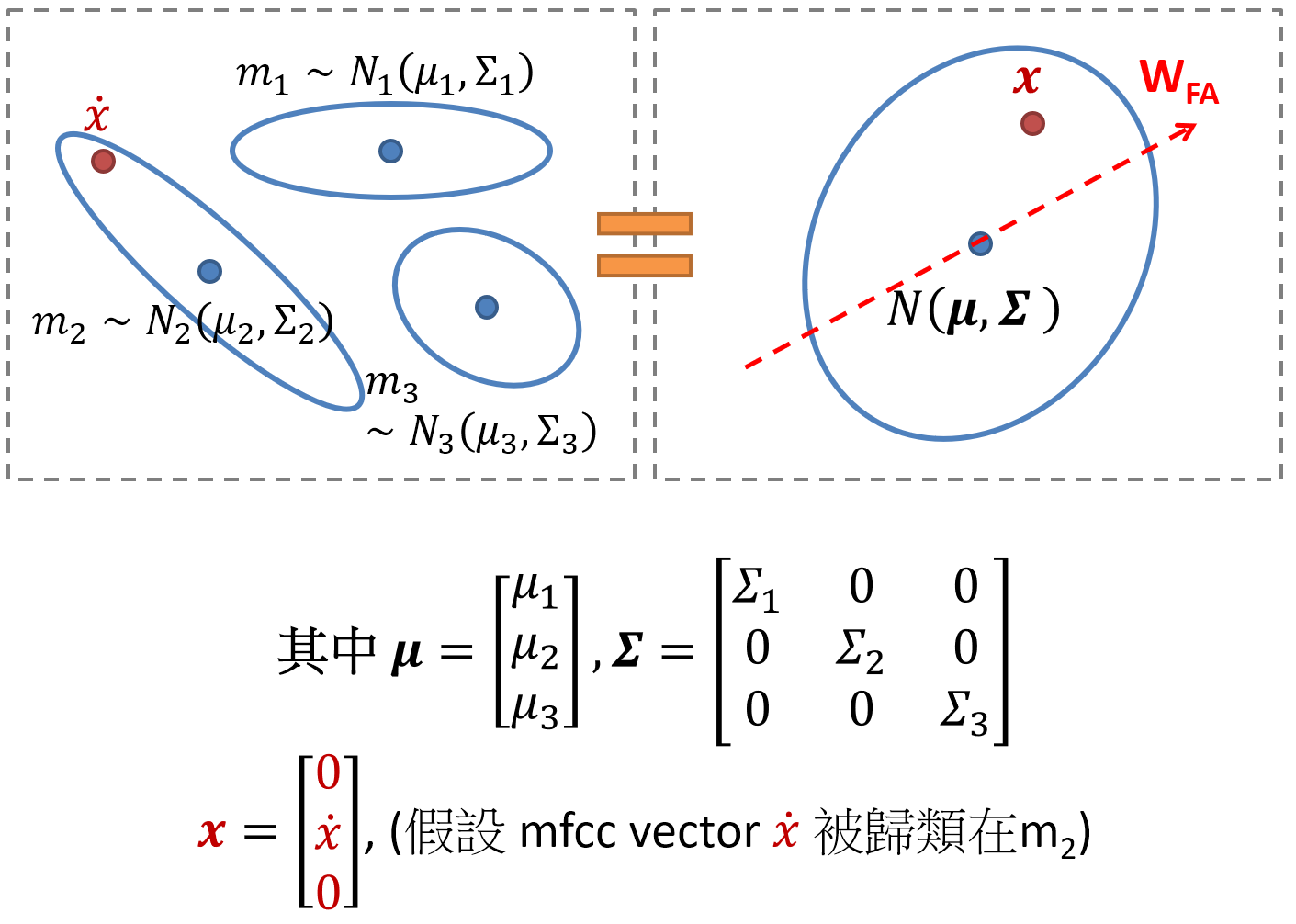
我們可以很容易驗證兩邊是等價的. 轉換成一個 Gaussian 好處就是我們可以直接使用 FA 降維, 而 ivector 就是該 FA 的 latent variable $z$. 如同 (2) 的定義:

$$\begin{align} p(x|z)=N(x|Wz+\mu,\Sigma) \\ \end{align}$$

這裡的 $\mu$ 是 UBM 的 supervector, $\Sigma$ 則如同上圖的定義, 是一個 block diagonal matrix, 每一個 block 對應一個 UBM mixture 的 covariance matrix. 因此 $\mu$ 和 $\Sigma$ 都是使用 UBM 的參數.

針對式 (25) 去更仔細了解其所代表的物理意義是很值得的, 所以我們多說一點. 由於我們已經知道這樣的一個 Gaussian 實際上代表了原來 mfcc space 的多個 Gaussians. 所以針對某一個特定的 ivector $z^*$ 由式 (25) 得知, 他有可能代表了下圖橘色的三個 Gaussians (也因此可能代表了某一個 speaker 的模型):

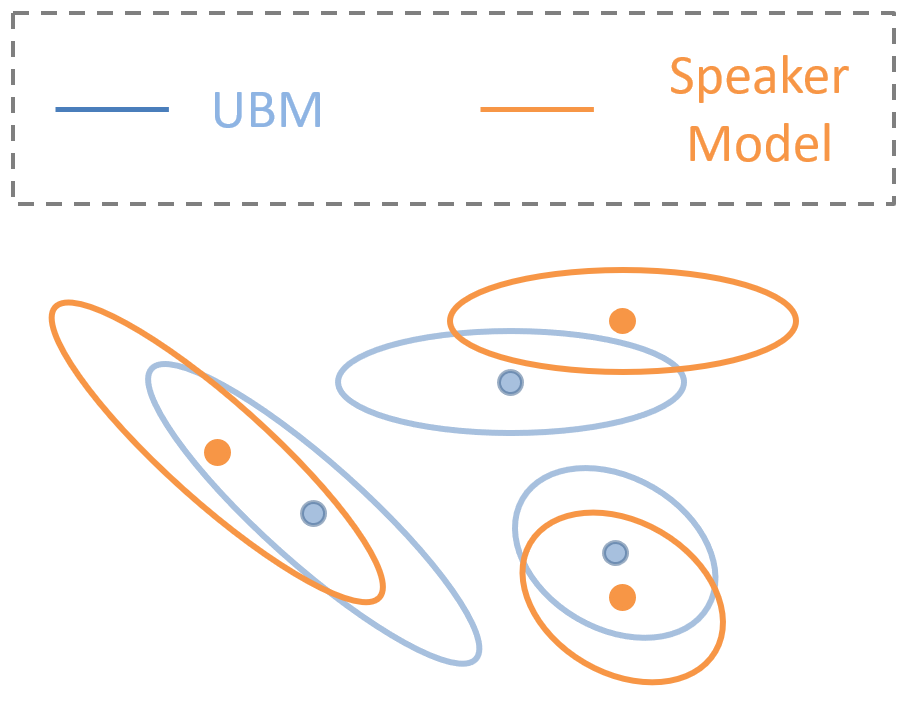
到目前為止所描述的 ivector 實際上是根據自己的理解將 2005 年 “Eigenvoice Modeling with Sparse Training Data“ 裡的 Proposition 1 (p348) 的設定描述出來. 如有錯誤還請來信指正.

該設定中, 每一個 mfcc vector 都會事先被歸類好屬於哪一個 mixture, 等於硬分類. 但是其實並不需要, 一個明顯的改進方法就是使用後驗概率來做軟分類. 直接看圖:

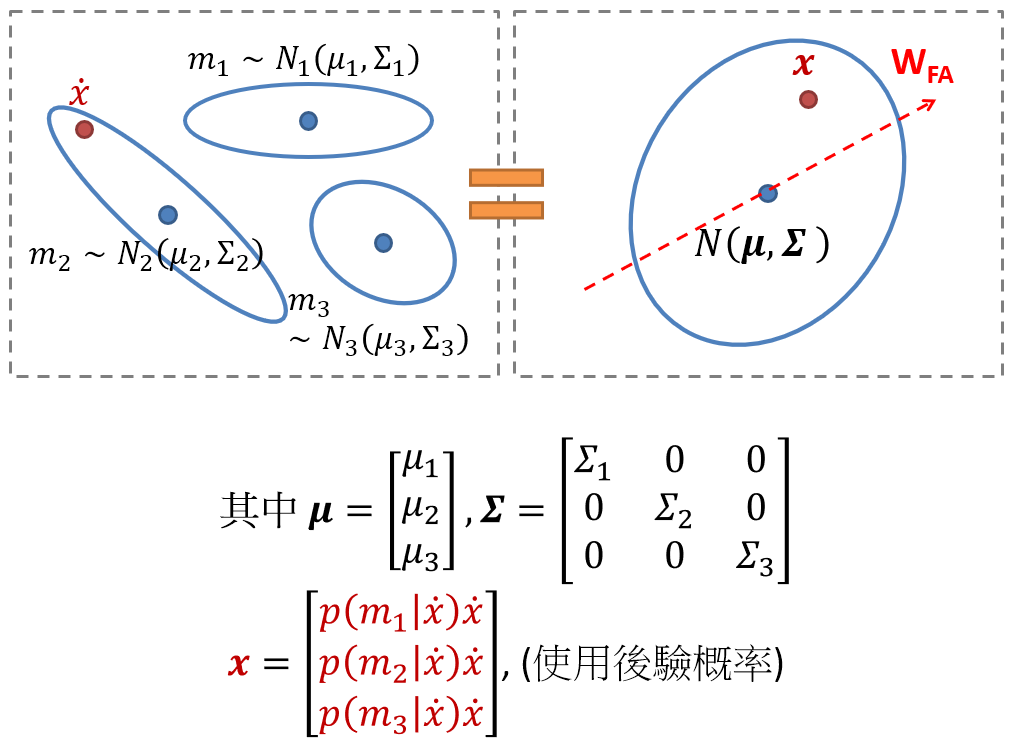
目前的 ivector 計算都使用這種方式, 例如 Microsoft Research 的 MSR Identity Toolbox. 該 toolbox 使用 “A Straightforward and Efficient Implementation of the Factor Analysis Model for Speaker Verification“ 的實作方式, 可以由論文的式 (2),(5) 看出使用後驗概率的設定.

最後多說一些語者識別的事情. ivector 主要是針對原高維空間 (mfcc-dim x component數量) 做降維, 而沒有去針對語者的訊息. 所以傳統流程會再經過 WCCN + LDA, 而 LDA 就會針對同一個語者盡量靠近, 而不同語者盡量拉開. 經過 LDA 後就可以用 $cos$ 計算相似度進行語者之間的打分.

但事實上, 更好的做法是用一個 PLDA 做更好的打分. 關於 PLDA 請參考這邊原始文章 “Probabilistic Linear Discriminant Analysis for Inferences About Identity“, 而 PLDA 更是與本篇的 FA 脫離不了關係!

總體來說 FA, MFA 對於目前的語者識別系統仍然十分關鍵, 縱使目前 Kaldi 使用了深度學習替換了 ivector, 但後端仍然接 PLDA.

Reference

自己實作的 Python MFA (含 Toy examples) github
Zoubin Ghahramani and Geoffrey E. Hinton, The EM Algorithm for Mixtures of Factor Analyzers
Bishop PRML
以前的 EM 筆記
以前的 GMM EM 筆記
i-vector 原始論文
PLDA 原始論文
Eigenvoice Modeling with Sparse Training Data
A Straightforward and Efficient Implementation of the Factor Analysis Model for Speaker Verification
MSR Identity Toolbox