本篇主要介紹什麼是 PGM, 以及一個很重要的應用 Part-of-Speech tagging. PGM 的部分主要圍繞在 “它是什麼?” 也就是 Koller 課程的 Representation. Inference 不討論, 因為自己也沒讀很深入 (汗), 而 Learning 就相當於 ML 裡的 training, 會在介紹 POS 時推導一下.
文章結構如下:
- What is Probabilistic Graphical Model (PGM)?
- What is Bayesian Network (BN)?
- What is Markov Network (MN)? (or Markov Random Field)
- What is Conditional Random Field (CRF)?
- Part-of-Speech (POS) Tagging
- References
文長…
What is Probabilistic Graphical Model (PGM)?
它是描述 pdf 的一種方式, 不同的描述方式如 directed/undirected graphical model, or Factor Graph 所能描述的 pdf 範圍是不同的. (ref: PRML) 其中 P 代表所有 distributions 的集合, U 和 D 分別表示 undirected 和 directed graphical models.
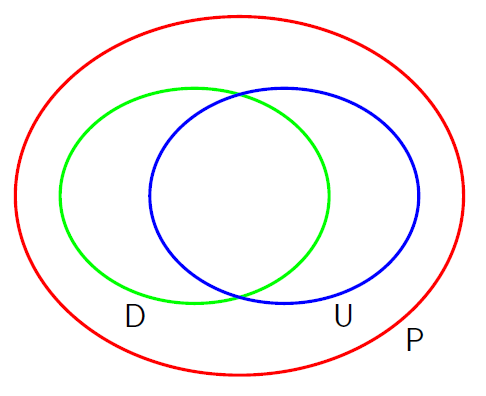
以有向無向圖來分如下:
- Directed Acyclic Graph (DAG): Bayesian Network
- Undirected Graph: Markov Network
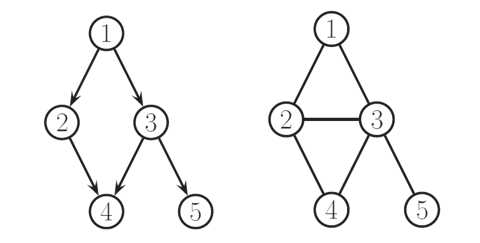
注意 BN 除了 directed 之外, 還需要 acyclic. 有了圖之後, 怎麼跟 distribution 產生連結的? 下面我們分別介紹 BN and MN.
What is Bayesian Network (BN)?
對於一個任意的 distibution over variables $x_1,…,x_V$ 我們可以用基本的 chain rule 拆解如下:
$$\begin{align} p(x_{1:V})=p(x_1)p(x_2|x_1)p(x_3|x_{1:2})...p(x_V|x_{1:V-1}) \end{align}$$變數的 order 可以任意排列, 舉例來說
$$\begin{align} p(x,y,z)\\ =p(x)p(y|x)p(z|x,y)\\ =p(x)p(z|x)p(y|x,z) \end{align}$$基於這種拆解我們可以很自然地想到, 不如把每個變數都當成 nodes, 再將 conditioning 的關係用 edges 連起來. 因此基本可以這麼表達:
$$\begin{align} p(x_{1:V}|G)=\prod_{t=1}^{V}p(x_t|pa(x_t)) \end{align}$$其中 $pa(x_t)$ 表示 node $x_t$ 的 parent nodes. 我們用式 (3) 和 (4) 當例子就可以畫出如下的圖:
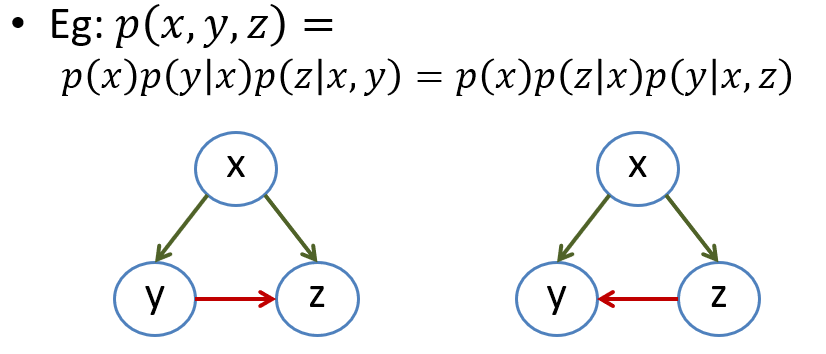
可以發現同一個 pdf 可以畫出多個 BN, 因此表達方式不是唯一.
Conditioning V.S. Independency
接著我們可能會想, 如果我們希望對 pdf 加一些獨立條件呢, 譬如如果希望 $x \perp y$, 是不是可以直接將圖中的 $x$ 和 $y$ 的 edge 拔掉就可以了呢? 先破題, 答案是不行. 同樣以上面的例子解釋, 如果我們用拔掉 edge 的話, 圖變成:
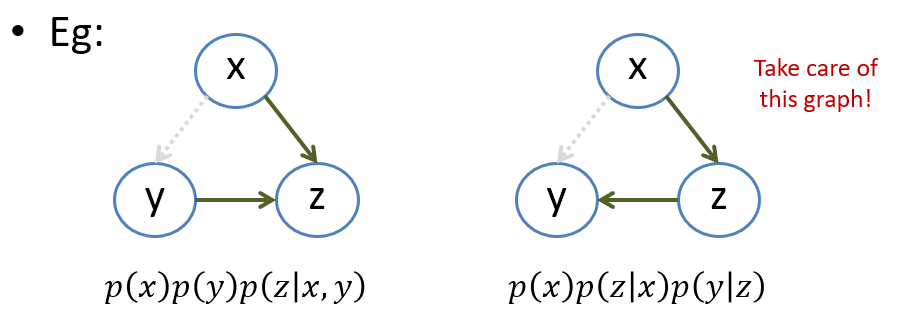
事實上這兩個圖已經各自表示不同的 distribution 了. 特別要注意在右圖中拔掉 $x$ and $y$ 的 edge 沒有造成 $x \perp y$. 解釋如下:

那究竟該如何從一個圖直接看出變數之間是否獨立? 為了解答這個問題, 我們先從簡單的三個 nodes 開始
Flow of Influence
三個 nodes 的 DAG 圖本質上就分以下三類, 其中 given 的變數我們通常以實心圓表示
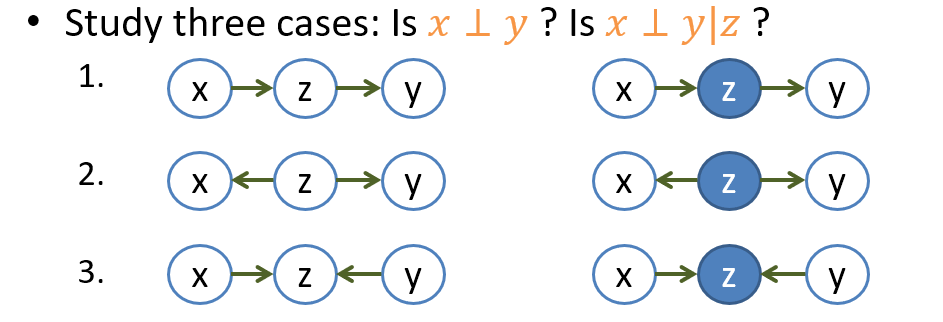
我們就個別討論
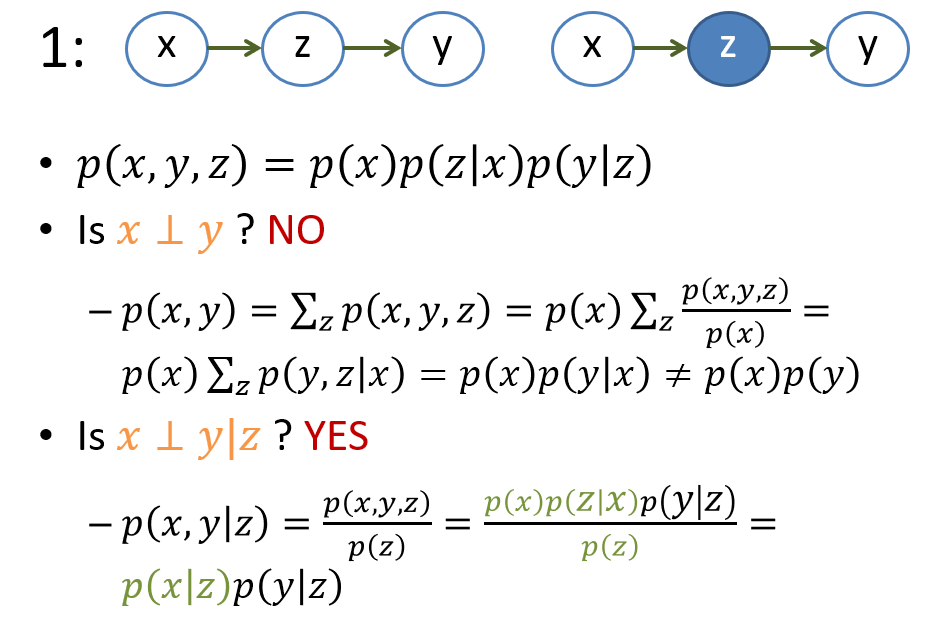
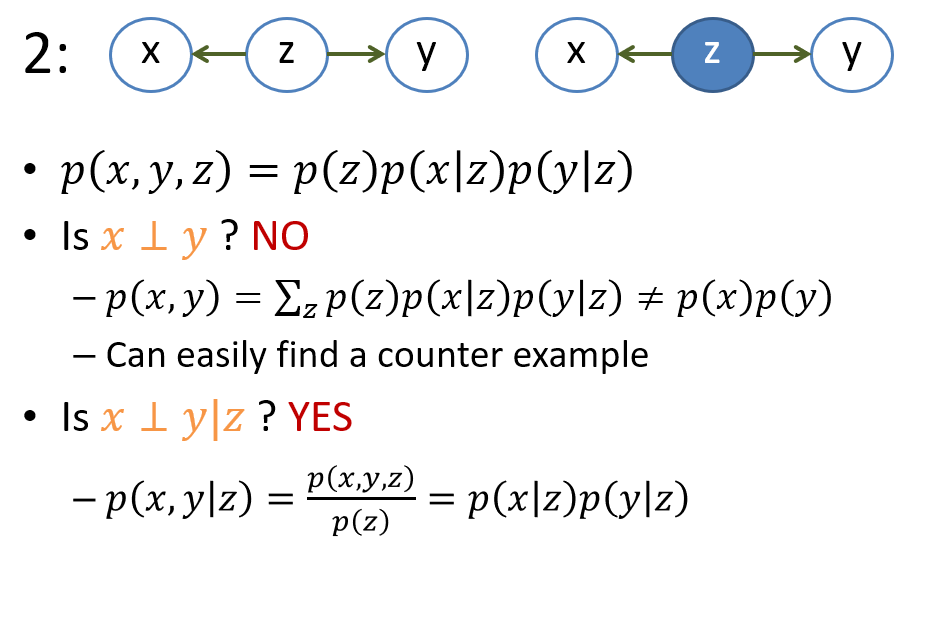

需要特別注意的是 case 3 的 v-structure, 行為跟其他兩種相反. 一種好記的方式是, 我們假設 given 的變量是一個石頭, 而 edges 可以想成是水流, 所以 given 變量就把水流擋住, 因此會造成獨立. 唯一個例外就是 v-structure, 行為剛好相反.
Active Trail in BN
我們可以很容易將三個 nodes 的 trail 擴展成 $V$ 個 nodes 的 trail. 因此可以很方便的觀察某條 trail 起始的 node 能否影響到最後的 node.
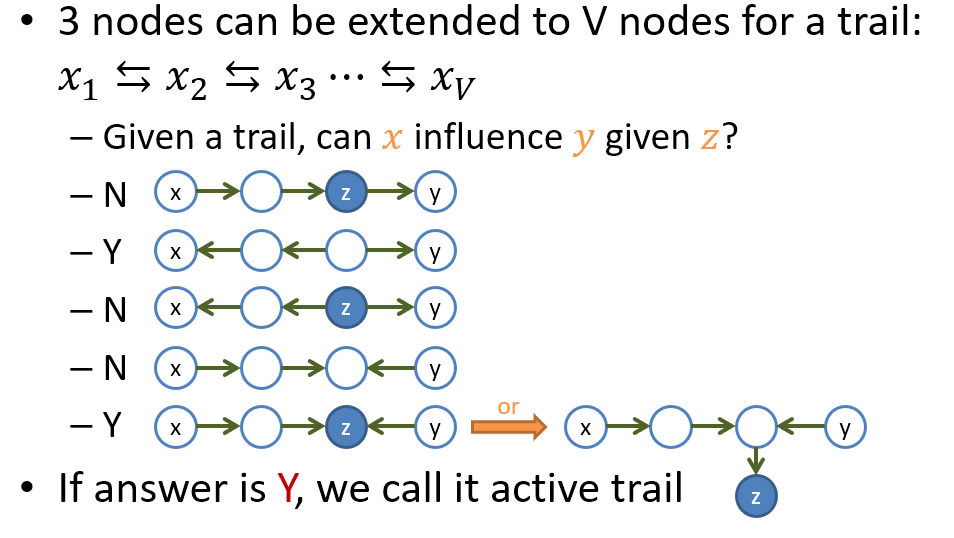
d-separation
繼續擴展! 我們假設在 BN $G$ 上 node $x$ and $y$ 有 $N$ 條 trails. 我們則可以藉由檢查每條 trail 是否 active 最終就會知道 $x$ 能否影響到 $y$.
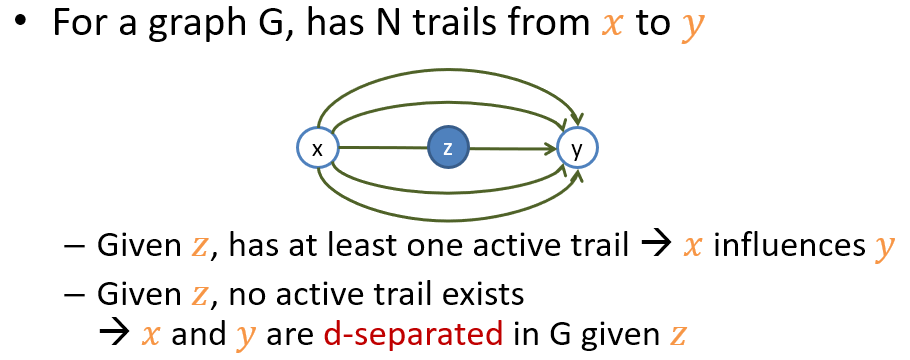
需要注意的是, 這些 d-separation 條件我們都可以直接從給定的 $G$ 上直接讀出來 (對於 distribution 沒有任何假設), 為了方便我們定義以下兩個 terms
$$\begin{align} CI(G)=\{\textbf{d-sep}(x,y|z)|x,y,z\textbf{ in }G\}\\ CI(p)=\{(x \perp y|z)|x,y,z\textbf{ in }G\}\\ \end{align}$$$CI(G)$ 所列出的 statements 是由 d-sep 所提供, 也就是說從 $G$ 直接讀出來的, 而 $CI(p)$ 才是真的對於 distribution $p$ 來說所有條件獨立的 statements.
OK, 到目前為止, 給定一個 BN $G$, 和一個 distribution $p$ (注意 $p$ 不一定可以被 $G$ 所表示), 他們之間的關係到底是什麼? 下面就要引出非常重要的定理 Factorization and Independent 的關係來說明
Factorization and Independent

白話文: 假設 $p$ 剛好可以寫成 $G$ 的 factorization 型式 (式 (5)), 則所有 $G$ 指出需要 $\perp$ 的 statements (根據 d-sep 所列), $p$ 都滿足

白話文: 假設所有 $G$ 指出需要 $\perp$ 的 statements (根據 d-sep 所列), $p$ 都滿足, 則 $p$ 可以寫成 $G$ 的 factorization 型式 (式 (5))
我們用 PRML book 裡一個具體的描述來說明 Thm1 and Thm2 之間的關係
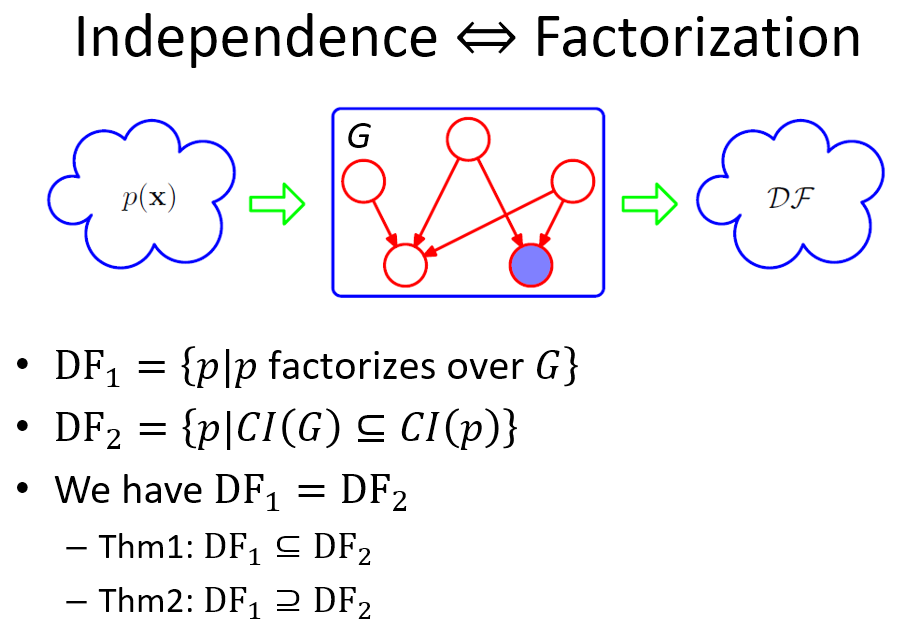
給定一個 $G$, 就好像一個篩子一樣, 根據兩種方式篩選 distribution
- $p$ 剛好可以寫成 $G$ 的 factorization 型式 (式 (5))
- $G$ 指出需要 $\perp$ 的 statements (根據 d-sep 所列), 剛好 $p$ 都滿足
用上面兩種篩選方式最後篩出來的 distributions 分別稱為 $DF1$ and $DF2$ 兩個 sets. 定理告訴我們它們式同一個集合!
Example
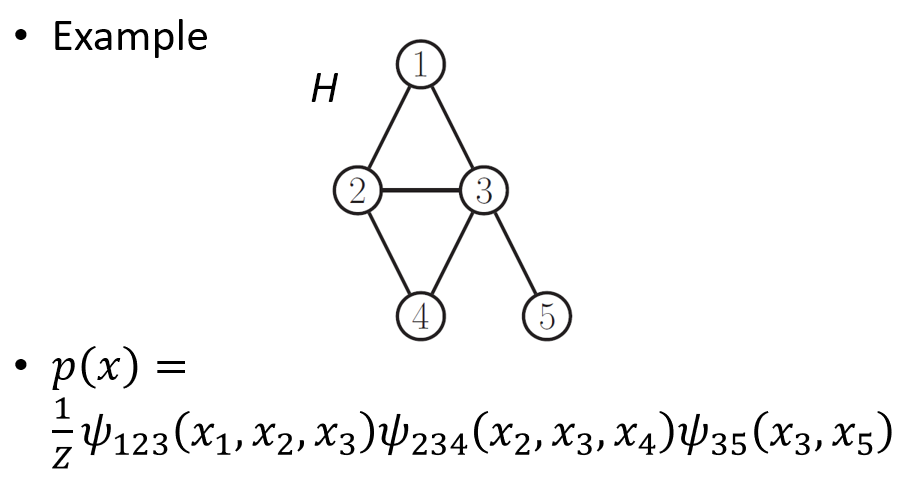
把下圖的 joint pdf 寫出來:
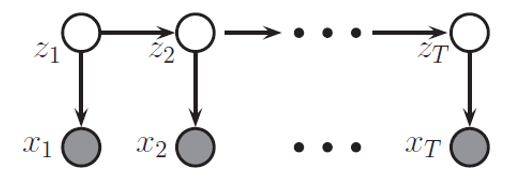
使用式 (5) 的方式寫一下, 讀者很快就發現, 這不就是 HMM 嗎?
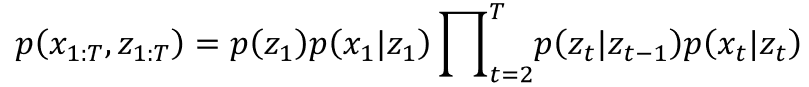
What is Markov Network (MN)?
Factorization
在解釋 MN 之前, 先了解一下什麼是 (maximal) clique.

因此, 我們可以用 maximal cliques 來定義一個 MN.
$$\begin{align} p(x)=\frac{1}{Z}\prod_{c\in\mathcal{C}}\psi_c(x_c) \end{align}$$$\mathcal{C}$ 是 maximal cliques 的集合. 然後 $Z$ 是一個 normalization term, 目的為使之成為 distribution.
$$\begin{align} Z=\sum_x\prod_{c\in\mathcal{C}}\psi_c(x_c) \end{align}$$舉個例子:
用無向圖的方式來表達 distribution 有一個很大的好處就是判斷 Active Trail 和 separation 變得非常非常簡單! 直接看下圖的說明
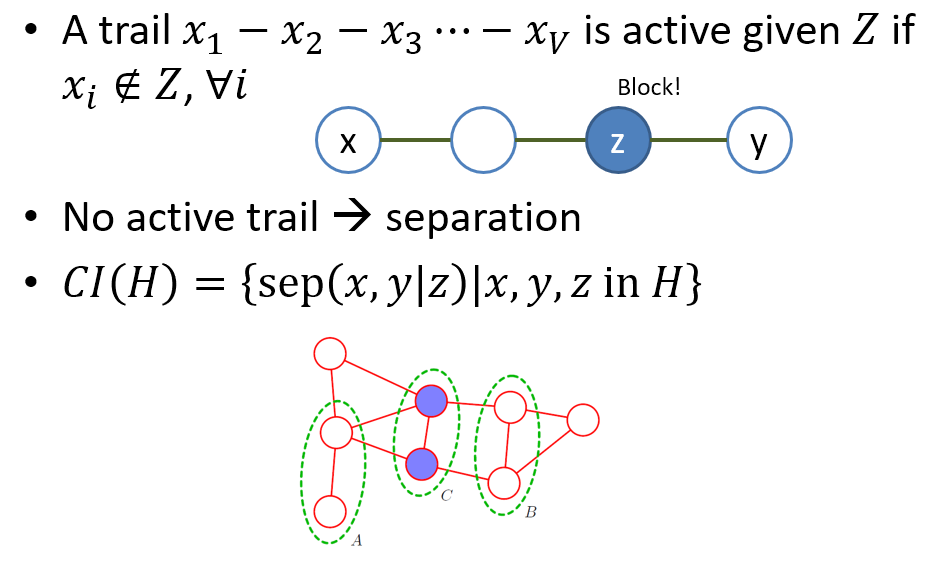
如同在 BN 時的討論, 給定一個 MN $H$, 和一個 distribution $p$ (注意 $p$ 不一定可以被 $H$ 所表示), 他們之間的關係可以由 Factorization and Independent 的定理來說明
Factorization and Independent
我們直接擷取 Kevin Murphy 書所列的定理, Hammersley-Clifford 定理

跟 BN 一樣, factorization iff independence, 但有一個重要的 assumption, 就是 distribution 必須 strictly positive (如上圖紅色框的部分). 我們一樣用 PRML 篩子的觀念來具體化:
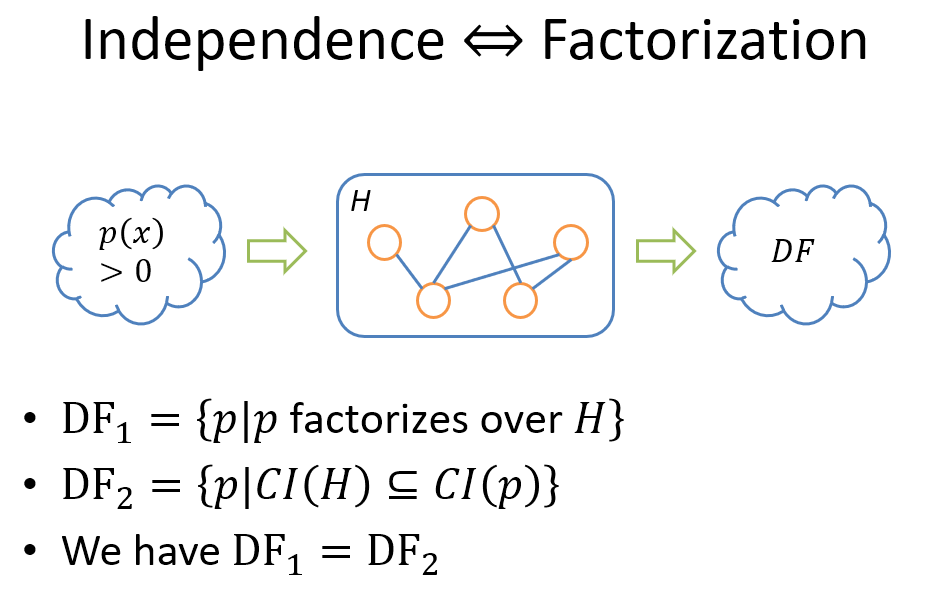
描述就跳過了.
Example
由於有 $p(x)>0$ 的假設在, 因此如果將 factor functions $\psi(x_c)$ 都使用 $exp$ 來定義的話, 整個 product 相乘後的 distribution 必定滿足 strictly positive. 因此 $exp$ 就不失為一種方便的 modeling 方式了

喘口氣的結論
到這裡, 我們可以
- 用 graph 簡單的表示出 joint pdf (用 factorization).
- 也可以從 graph 中看出 conditional independence (用 active tail, separation)
因此我們可以針對要 model 的問題利用 graph 來描述 joint pdf 了. 但是光描述好 model 沒用, 我們還需要 inference (test) and learning (train). Inference 非常推薦看 PRML ch8, 講如何對 tree graph 做 sum-product algorithm (belief propagation) 非常精彩.
接著如何推廣到一般 general graph 則可以使用 junction tree algorithm (推薦看這篇文章, 解釋非常棒!). 上述兩種方式都屬於 exact inference, 對於一些情形仍會需要 exponential time 計算, 因此我們需要 variational inference 或 sampling 的方式算 approximation.
最後有關 learning 我們使用接下來的 POS tagging 當範例推導一下. 但別急, 在講 POS 之前我們得先談一個重要的東西, Conditional Random Field.
What is Conditional Random Field (CRF)?

如同上圖的說明, 基本上 CRF 仍舊是一個 MN, 最大的差別是 normalization term 如今不再是一個 constant, 而是 depends on conditioning 的變數 $x$.
一個在 sequence labeling 常用的 CRF 模型是 Linear-Chain CRF
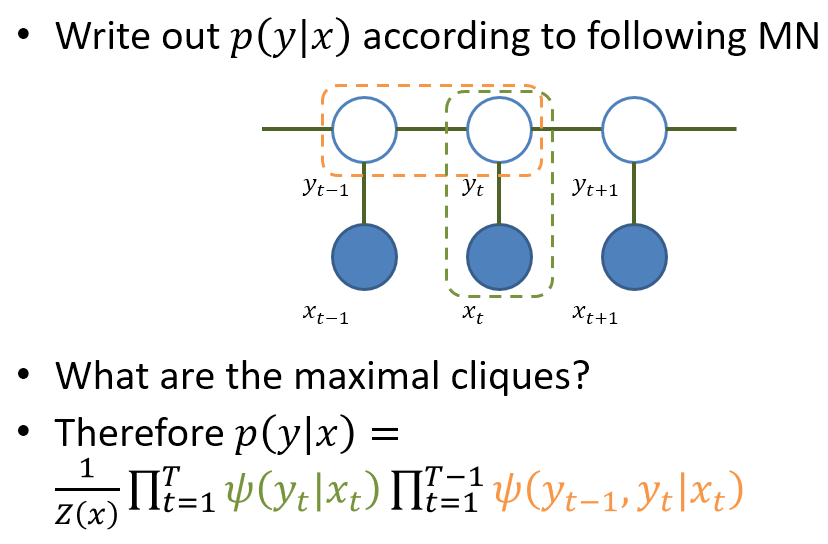
有了這些概念後我們就可以說說 POS 了
Part-of-Speech (POS) Tagging
擷取自李宏毅教授上課投影片
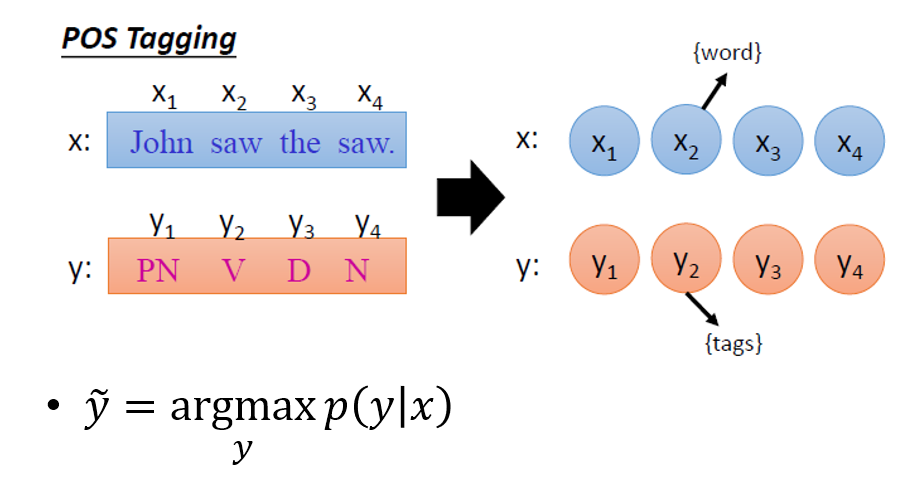
基本上就是給定一個 word sequence $x$, 我們希望找出哪一個詞性標註的 sequence $y$ 會使得機率最大. 機率最大的那個 $y$ 就是我們要的詞性標註序列.
使用現學現賣的 PGM modeling 知識, 我們可以使用 BN or MN 的方式描述模型
- BN: Hidden Markov Model (HMM)
- MN: Linear chain CRF with log-linear model
有向圖 HMM 方法
一樣擷取自李宏毅教授上課投影片
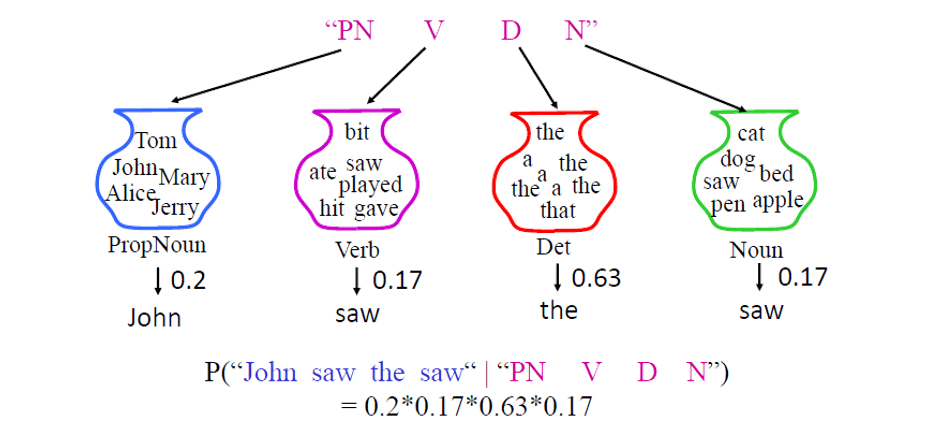
還記得本文前面講 BN 時的 HMM example 嗎? $y$ 就是詞性, $x$ 就是字. HMM 是在 model 給定詞性序列情形下的字序列 distribution. 了解語音辨識的童鞋門應該再熟悉不過了, 只不過這裡問題比較簡單, 在語音辨識裡, 我們不會針對每個 frame 去標註它是屬於哪一個發音的 state, 因此標註其實是 hidden 的. 但在這裡每個 word 都會有一個對應正確答案的詞性標註, 沒有 hidden 資訊, 因此也不需要 EM algorithm, 簡單的 counting 即可做完訓練. that all …
無向圖 CRF 方法
精確說是 Linear chain CRF with log-linear model
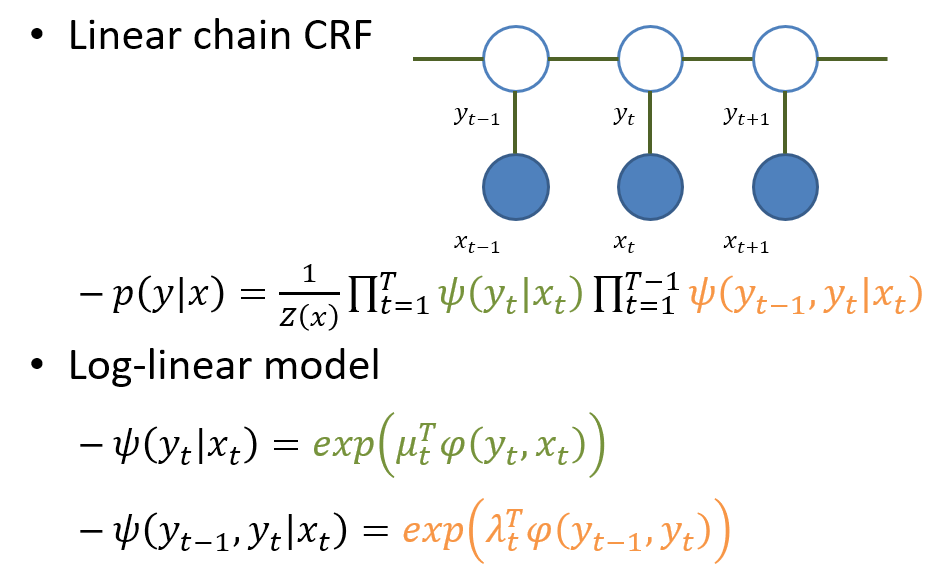
我們把 log-linear model 的 factor 帶入 linear chain CRF 中, 注意其中 $\phi$ 是需要定義的特徵函數, 我們這裡先假設可以抽取出 $K$ 維. 因此可以推導如下
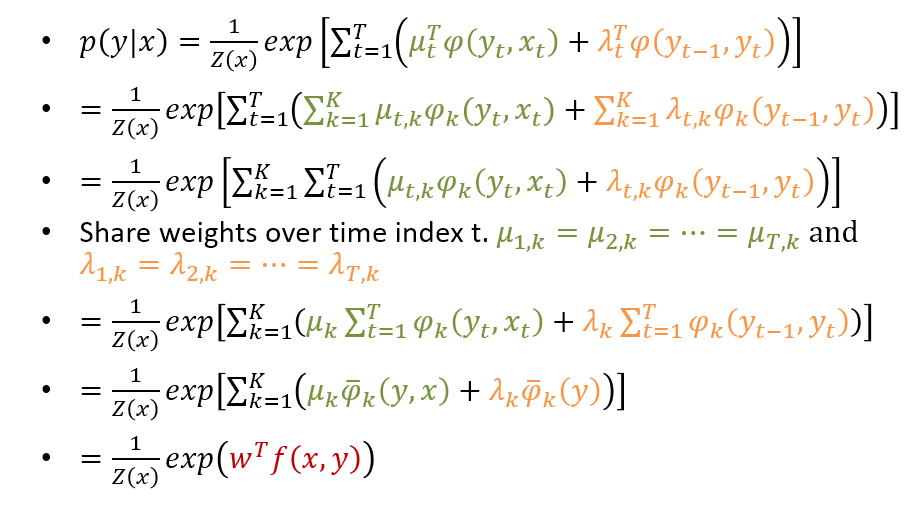
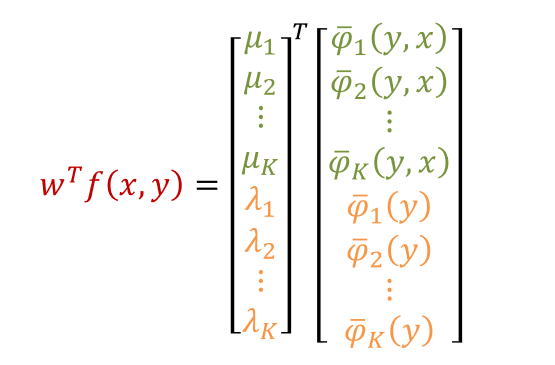
實作上我們會針對時間 share weights, 這是因為句子都是長短不一的, 另一方面這樣做也可以大量減少參數量. 所以最後可以簡化成一個 weigth vector $w$ 和我們合併的特徵向量 $f(x,y)$ 的 log-linear model.
Learning
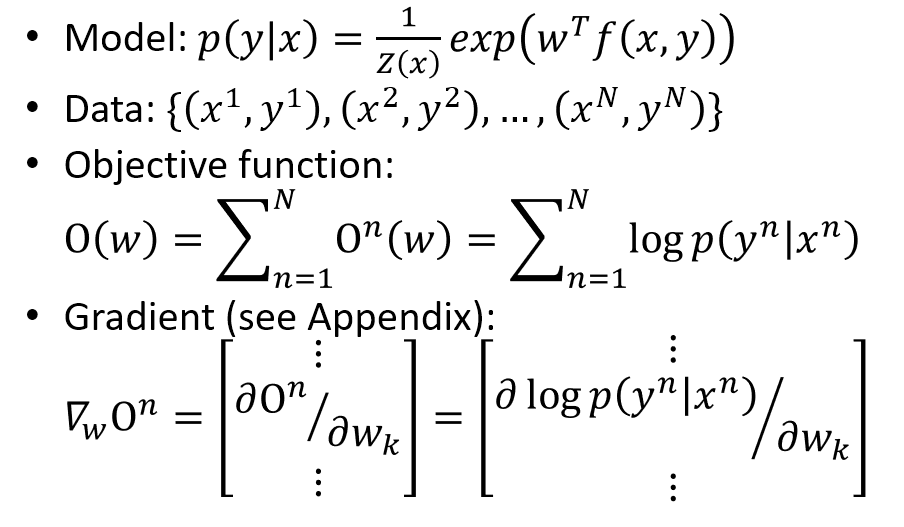
目標函數就是在最大化 CRF 的 likelihood. 採用 gradient method. 而 gradient 的推導事實上也不困難, 只要花點耐心即可了解
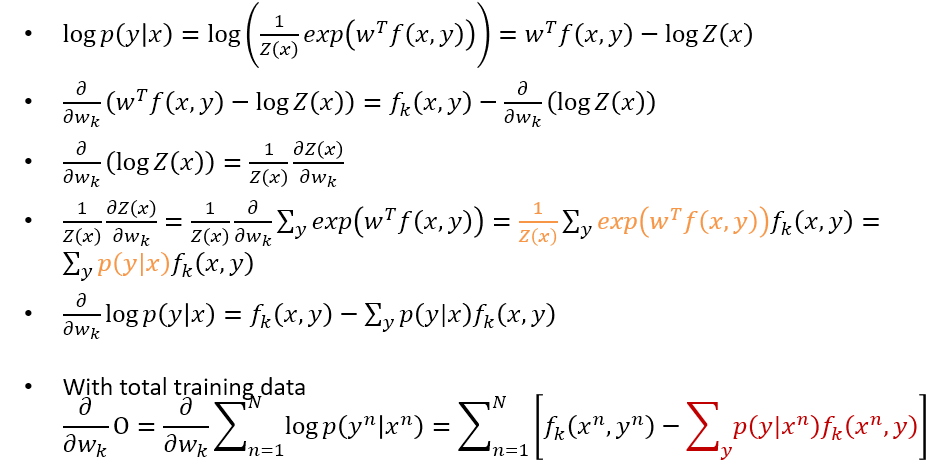
但是其實我說不困難只說對了一半, 紅色的地方事實上需要跑 inference 才可以得到, 好在 linear-chain 架構下正好可以用 Viterbi 做前向後算計算, 這部分的式子可以跟 “李航 統計學習方法“ 這本書的 p201 式 (11.34) 銜接上, 該式寫出了前向後向計算.
Tool
CRF++ 做為語音辨識的後處理十分好用的工具, in c++.
References
PGM 博大精深, 這個框架很完整且嚴謹, 值得我後續花時間研讀, 有機會看能否將 Koller 的課程上過一次看看.
通常這麼說就表示 …. hmm…你懂得
- Bishop PRML book
- Kevin Murphy book
- Junction Tree Algorithm
- 李航 統計學習方法
- 李宏毅老師 ML 課程