Variational Inference and VAE Notes

---

前一陣子學習了 Variational Inference, 因為自己記性只有 LSTM 沒有 L, 所以趕快記下筆記. 學得還是很粗淺, 又是一個大坑阿.
監督學習不外乎就是 training 和 testing (inference). 而 inference 在做的事情就是在計算後驗概率 $p(z|x)$. 在 PGM 中通常是 intractable, 或要找到 exact solution 的計算複雜度太高, 這時 VI 就派上用場了. VI 簡單講就是當 $p(z|x)$ 不容易得到時, 可以幫你找到一個很好的近似, $q(z)$.

放上一張 NIPS 2016 VI tutorial 的圖, 非常形象地表示 VI 做的事情: 將找 $p(z|x)$ 的問題轉化成一個最佳化問題.

---

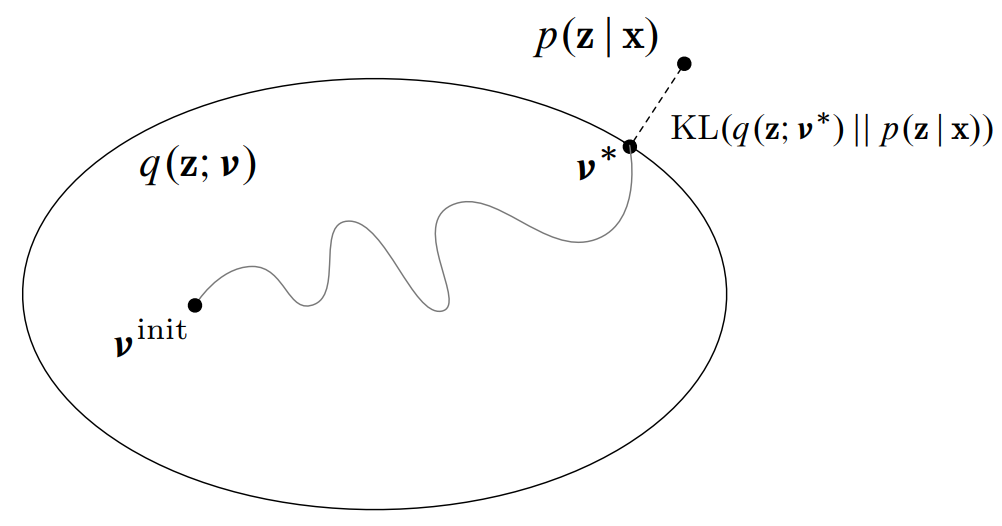
怎麼看作最佳化問題?

我們要找到一個 $q(z)$ 去逼近 $p(z|x)$, 因此需要計算兩個機率分佈的距離, 而 KL-divergence 是個很好的選擇 (雖然不滿足數學上的距離定義). 所以我們的目標就是希望 $KL(q(z)\Vert p(z|x))$ 愈小愈好, 接著我們對 KL 定義重新做如下的表達:

$$\begin{align} KL\left(q(z)\Vert p(z|x)\right)=-\sum_z q(z)\log\frac{p(z|x)}{q(z)}\\ =-\sum_z q(z)\left[\log\frac{p(x,z)}{q(z)}-\log p(x)\right]\\ =-\sum_z q(z)\log\frac{p(x,z)}{q(z)}+\log p(x) \end{align}$$

得到這個非常重要的式子:

$$\begin{align} \log p(x)=KL\left(q(z)\Vert p(z|x)\right)+ \color{red}{ \sum_z q(z)\log\frac{p(x,z)}{q(z)} } \\ =KL\left(q(z)\Vert p(z|x)\right)+ \color{red}{ \mathcal{L}(q) } \\ \end{align}$$

為什麼做這樣的轉換呢? 這是因為通常 $p(z|x)$ 很難得到, 但是 complete likelihood $p(z,x)$ 通常很好求.
觀察 (5), 注意到在 VI 的設定中 $\log p(x)$ 跟我們要找的 $q(z)$ 無關, 也就造成了 $\log p(x)$ 是固定的. 由於 $KL\geq 0$, 讓 $KL$ 愈小愈好等同於讓 $\mathcal{L}(q)$ 愈大愈好. 因此 VI 的目標就是藉由最大化 $\mathcal{L}(q)$ 來迫使 $q(z)$ 接近 $p(z|x)$.

$\mathcal{L}(q)$ 可以看出來是 marginal log likelihood $\log p(x)$ 的 lower bound. 因此稱 variational lower bound 或 Evidence Lower BOund (ELBO).

---

ELBO 的 gradient

我們做最佳化都需要計算 objective function 的 gradient. 讓要找的 $q$ 由參數 $\nu$ 控制, i.e. $q(z;\nu)$, 所以我們要找 ELBO 的 gradient 就是對 $\nu$ 微分.

$$\begin{align} \mathcal{L}(\nu)=\mathbb{E}_{z\sim q}\left[\log p(x,z) - \log q(z;\nu)\right]\\ \Rightarrow \nabla_{\nu}\mathcal{L}(\nu)=\nabla_{\nu}\left(\mathbb{E}_{z\sim q}\left[\log p(x,z) - \log q(z;\nu)\right]\right)\\ \mbox{Note }\neq \mathbb{E}_{z\sim q}\left(\nabla_{\nu}\left[\log p(x,z) - \log q(z;\nu)\right]\right)\\ \end{align}$$

注意 (8) 不能將 Expectation 與 derivative 交換的原因是因為要微分的 $\nu$ 與要計算的 Expectation 分布 $q$ 有關. 下面會提到一個很重要的技巧, Reparameterization trick, 將 Expectation 與 derivative 交換, 而交換後有什麼好處呢? 下面提到的時候再說明.

回到 (7) 展開 Expectation 繼續計算 gradient, 直接用 NIPS slide 結果如下:

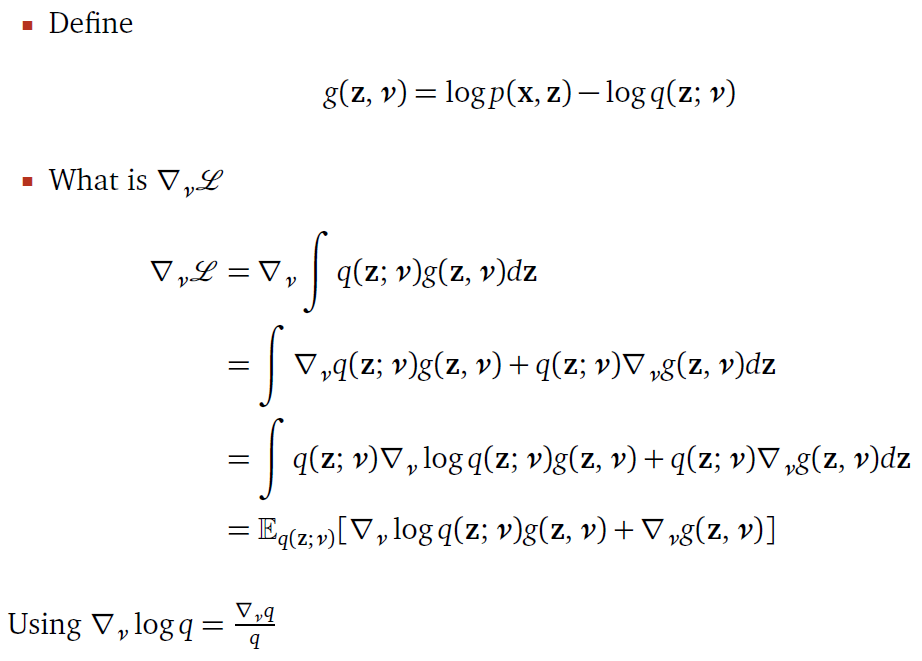
計算一個機率分佈的 Expectation 可用 Monte Carlo method 採樣, 例如採樣 $T$ 個 samples

$$\begin{align} \mathbb{E}_{z\sim q}f(z)\approx\frac{1}{T}\sum_{t=1}^Tf(z)\mbox{, where }z\sim q \end{align}$$

因此 gradient 可以這麼大致找出來, 不過這方法找出來的 gradient 與真實的 gradient 存在很大的誤差, 換句話說, 這個近似的 gradient variance 太大了. 原因兩個

1. $q$ 本身就還在估計, 本身就不準確了
2. Monte Carlo method 採樣所造成的誤差

下一段的 reparameterization trick 就可以去除掉上面第一個誤差, 因此估出來的 gradient 就穩定很多.

---

Reparameterization Trick

我們用 Gaussian 舉例, 令 $q$ 是 Gaussian, $q(z;\mu,\sigma)=\mathcal{N}(\mu,\sigma)$, 其中 $\nu=${$\mu,\sigma$}, 而我們其實可以知道 $z=\mu+\sigma \epsilon$, where $\epsilon\sim\mathcal{N}(0,\mathbf{I})$. 因此:

$$\begin{align} \mathcal{L}(\nu)=\mathbb{E}_{z\sim q}\left[\log p(x,z)-\log q(z;\nu)\right]\\ =\mathbb{E}_{ \color{red}{ \epsilon\sim \mathcal{N}(0,\mathbf{I}) } }\left[\log p(x, \color{red}{ \mu+\sigma \epsilon } )-\log q( \color{red}{ \mu+\sigma \epsilon } ;\nu)\right] \end{align}$$

這時候我們計算 ELBO 的 gradient 時, 我們發現 $\nu$ 與 Expectation 的分佈, $\mathcal{N}(0,\mathbf{I})$, 無關了! 因此 (7) 套用上面的 trick 就可以將 Expectation 與 derivative 交換. 結果如下:

$$\begin{align} \nabla_{\mu}\mathcal{L}(\nu)=\mathbb{E}_{\epsilon\sim \mathcal{N}(0,\mathbf{I})}\left[\nabla_{\mu}\left(\log p(x,\mu+\sigma \epsilon) - \log q(\mu+\sigma \epsilon;\nu)\right)\right]\\ \approx\frac{1}{T}\sum_{t=1}^T \nabla_{\mu}\left( \log p(x,\mu+\sigma \epsilon) - \log q(\mu+\sigma \epsilon;\nu) \right)\mbox{, where }\epsilon\sim\mathcal{N}(0,\mathbf{I})\\ \end{align}$$

在上一段計算 ELBO gradient 所造成誤差的第一項原因就不存在了, 因此我們用 reparameterization 得到的 gradient 具有很小的 variance. 這個 github 做了實驗, 發現 reperameterization 的確大大降低了估計的 gradient 的 variance.

$$\begin{align} \nabla_{\mu}\left(\log p(x,\mu+\sigma \epsilon) - \log q(\mu+\sigma \epsilon;\nu)\right) \end{align}$$

怎麼計算呢? 我們可以使用 Tensorflow 將要計算 gradient 的 function 寫出來, tf.gradients 就能算

---

VAE

Variational Inference 怎麼跟 Neural Network 扯上關係的? 這實在很神奇.
我們先來看看 ELBO 除了 (6) 的寫法, 還可以這麼表示:

$$\begin{align} \mathcal{L}(\nu)=\mathbb{E}_{z\sim q}\left[\log p(x,z) - \log q(z;\nu)\right]\\ =\mathbb{E}_{z\sim q}\left[ \log p(x|z) + \log p(z) - log q(z;\nu) \right]\\ =\mathbb{E}_{z\sim q}\left[ \log p(x|z)\right] + \mathbb{E}_{z\sim q}\left[ \log \frac{p(z)}{q(z;\nu)}\right]\\ =\mathbb{E}_{z\sim q}\left[ \log p(x|z)\right] - KL(q(z;\nu)\|p(z))\\ \end{align}$$

我們讓 $p(x|z)$ 被參數 $\theta$ 所控制, 所以最後 ELBO 如下:

$$\begin{align} \mathcal{L}(\nu,\theta)=\mathbb{E}_{z\sim q}\left[ \log \color{orange}{ p(x|z,\theta) } \right] - KL( \color{blue}{ q(z;\nu) } \|p(z))\\ \end{align}$$

讓我們用力看 (19) 一分鐘
接著在用力看 (19) 一分鐘
最後在用力看 (19) 一分鐘

有看出什麼嗎? … 如果沒有, 試著對照下面這張圖

Encoder 和 Decoder 都同時用 NN 來學習, 這裡 $\nu$ 和 $\theta$ 分別表示 NN 的參數, 而使用 Reparameterization trick 來計算 ELBO 的 gradient (14) 就相當於在做這兩個 NN 的 backprop.

但是上圖的 Encoder 產生的是一個 pdf, 而給 Decoder 的是一個 sample $z$, 這該怎麼串一起? VAE 的做法就是將 $q(z)$ 設定為 diagonal Gaussian, 然後在這個 diagonal Gaussian 採樣出 $T$ 個 $z$ 就可以丟給 Decoder. 使用 diagonal Gaussian 有兩個好處:

1. 我們可以用 reparameterization trick, 因此採樣只在標準高斯上採樣, 自然地 Encoder 的 output 就是 $\mu$ 和 $\sigma$ 了.
2. (19)的 KL 項直接就有 closed form solution, 免掉算 expectation (假設$p(z)$也是Gaussian的話)

根據1, 架構改動如下:

將原來的 ELBO (10) 轉成 (19) 來看的話, 還可以看出一些資訊.
當最大化 (19) 的時候

• RHS 第一項要愈大愈好 (likelihood 愈大愈好), 因此這一項代表 reconstruct error 愈小愈好.
• RHS 第二項, 也就是 $KL(q(z;\nu)\Vert p(z))$ 則要愈小愈好. 因此會傾向於讓 $q(z;\nu)$ 愈接近 $p(z)$ 愈好. 這可以看做 regularization.

但是別忘了一開始說 VI 的做法就是藉由最大化 ELBO 來迫使 $q(z;\nu)$ 接近 $p(z|x)$, 而上面才說最大化 ELBO 會傾向於讓 $q(z;\nu)$ 接近 $p(z)$.
這串起來就說 $q(z;\nu)$ 接近 $p(z|x)$ 接近 $p(z)$. 在 VAE 論文裡就將 $p(z)$ 直接設定為 $\mathcal{N}(0,\mathbf{I})$. 因此整個 VAE 訓練完的 Encoder 的 $z$ 分布會有高斯分布的情形.

Conditional VAE (CVAE)

原來的 VAE 無法控制要生成某些類別的圖像, 也就是隨機產生 $z$ 不知道這會對應到哪個類別. CVAE 可以根據條件來產生圖像, 也就是除了給 $z$ 之外需要再給 $c$ (類別) 資訊來生成圖像. 怎麼辦到的呢? 方法簡單到我嚇一跳, 看原本論文有點迷迷糊糊, 但這篇文章解釋得很清楚! 簡單來說將原來的推倒全部加上 condition on $c$ 的條件. 從 (4) 出發修改如下:

$$\begin{align} \log p(x \color{red}{ | c } ) =KL\left(q(z \color{red}{ | c } )\Vert p(z|x, \color{red}{ c } )\right)+ \sum_z q(z \color{red}{ | c } )\log\frac{p(x,z \color{red}{ | c } )}{q(z \color{red}{ | c } )} \\ \end{align}$$

用推導 VAE 一模一樣的流程, 其實什麼都沒做, 只是全部 conditioned on $c$ 得到 (19) 的 condition 版本

$$\begin{align} \mathcal{L}(\nu,\theta \color{red}{ | c } )=\mathbb{E}_{z\sim q}\left[ \log \color{orange}{ p(x|z,\theta, \color{red}{ c } ) } \right] - KL( \color{blue}{ q(z;\nu \color{red}{ | c } ) } \|p(z))\\ \end{align}$$

這說明了我們在學 Encoder 和 Decoder 的 NN 時必須加入 conditioned on $c$ 這個條件! NN 怎麼做到這點呢? 很暴力, 直接將 class 的 one-hot 跟原來的 input concate 起來就當成是 condition 了. 因此 CVAE 的架構如下:

實作細節就不多說了, 直接參考 codes

由於我們的 condition 是 one-hot, 如果同時將兩個 label 設定為 1, 是不是就能 conditioned on two classes 呢? 實驗如下

• conditioned on ‘0’ and ‘4’

• conditioned on ‘1’ and ‘3’

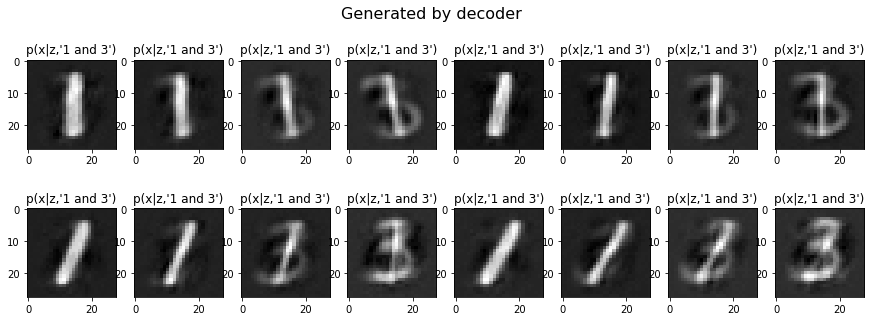
另外, 如果給的 condition 值比較小, 是不是就可以產生比較不是那麼確定的 image 呢? 我們嘗試 conditioned on ‘4’ 且值從 0.1 (weak) 到 1.0 (strong), 結果如下:

這個 condition 值大小還真有反應強度呢! Neural network 真的很神奇阿~

---

Mean Field VI

讓我們拉回 VI. Mean Field 進一步限制了 $q$ 的範圍, 它假設所有控制 $q$ 的參數 {$\nu_i$} 都是互相獨立的, 這樣所形成的函數空間稱為 mean-field family. 接著採取 coordinate ascent 方式, 針對每個 $\nu_i$ 獨立 update. 這種 fatorized 的 $q$ 一個問題是 estimate 出來的分布會太 compact, 原因是我們使用的指標是 $KL(q|p)$, 詳細參考 PRML Fig 10.2. 放上 NIPS 2016 slides, 符號會跟本文有些不同, 不過總結得很好:

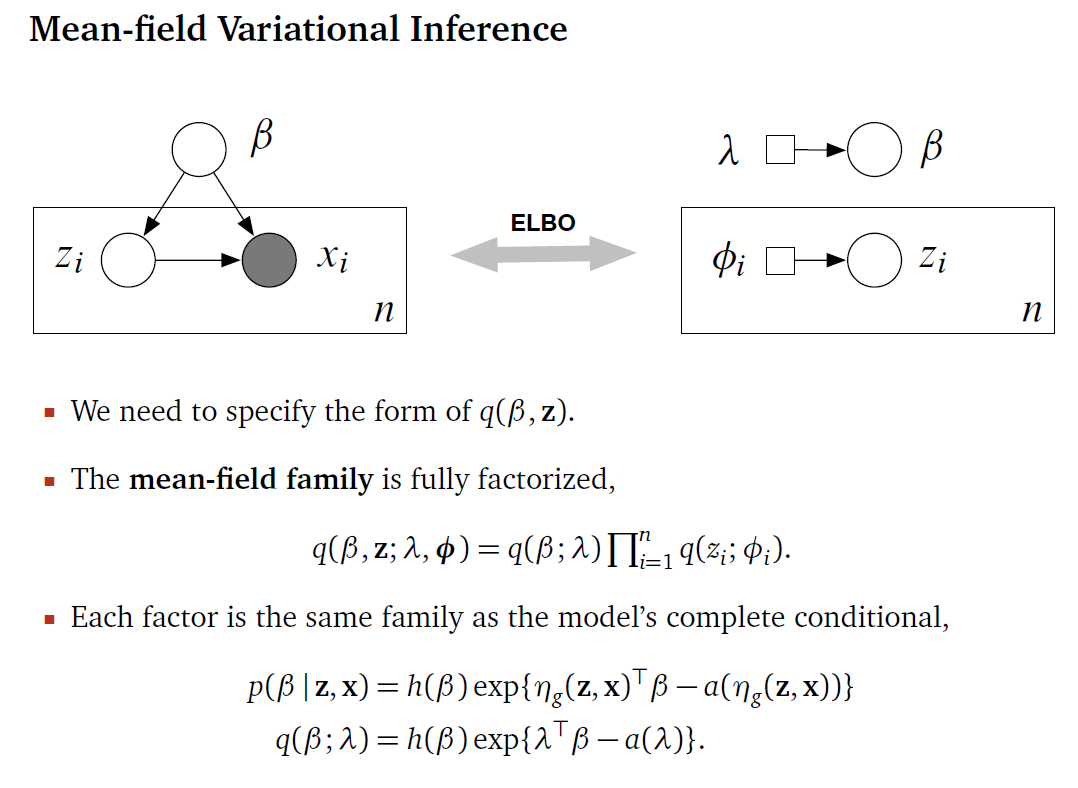
另外想了解更多 Mean Field VI 或是透過例子了解, 推薦以以下兩個資料:

• Variational Inference tutorial series by Chieh Wu
• Variational Coin Toss by Björn Smedman

---

Reference

1. Variational Inference tutorial series by Chieh Wu
2. Variational Inference: Foundations and Modern Methods (NIPS 2016 tutorial)
3. Reparameterization Trick
4. Goker Erdogan 有很好的 VAE, VI 文章
5. Conditional VAE 原論文
6. Conditional VAE 好文章
7. Variational Coin Toss by Björn Smedman
8. My CVAE TF Practice

---

Appendix: EM 跟 VI 很像阿

在一般 EM 的設定上, 我們是希望找到一組參數 $\tilde{\theta}$ 可以讓 marginal likelihood $\log p(x|\theta)$ 最大, formally speaking:

$$\begin{align} \tilde{\theta}=\arg\max_\theta \log p(x|\theta) \end{align}$$

如同 (4) 和 (5), 此時要求的變數不再是 $q$, 而是 $\theta$:

$$\begin{align} \log p(x|\theta)=KL\left(q(z)\Vert p(z|x,\theta)\right)+\sum_z q(z)\log\frac{p(x,z|\theta)}{q(z)}\\ =KL\left(q(z)\Vert p(z|x,\theta)\right)+ \color{orange}{ \mathcal{L}(q,\theta) } \\ \end{align}$$

此時的 $\log p(x|\theta)$ 不再是固定的 (VI是), 而是我們希望愈大愈好. 而我們知道 $\mathcal{L}(q,\theta)$ 是它的 lower bound 這點不變, 因此如果 lower bound 愈大, 則我們的 $\log p(x|\theta)$ 就當然可能愈大.

首先注意到 (23) 和 (24) 針對任何的 $q$ 和 $\theta$ 等式都成立, 我們先將 $\theta$ 用 $\theta^{old}$ 以及 $q(z)$ 用 $p(z|x,\theta^{old})$ 代入得到:

$$\begin{align} \log p(x|\theta^{old})= KL\left(p(z|x,\theta^{old})\Vert p(z|x,\theta^{old})\right)+\mathcal{L}(p(z|x,\theta^{old}),\theta^{old})\\ =0+\mathcal{L}(p(z|x,\theta^{old}),\theta^{old})\\ \leq\max_{\theta}\mathcal{L}(p(z|x,\theta^{old}),\theta)\\ \end{align}$$

接著求

$$\begin{align} \theta^{new}=\arg\max_{\theta} \mathcal{L}(p(z|x,\theta^{old}),\theta) \end{align}$$

如此 lower bound 就被我們提高了.
(28) 就是 EM 的 M-step, 詳細請看 PRML Ch9.4 或參考下圖理解

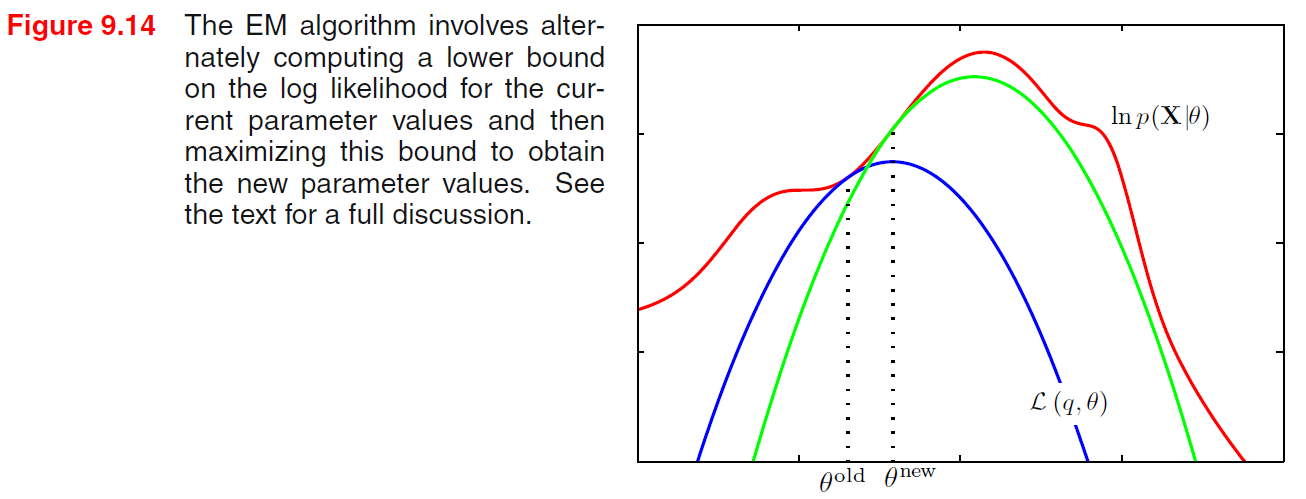
“$q(z)$ 用 $p(z|x,\theta^{old})$ 代入” 這句話其實有問題, 因為關鍵不就是 $p(z|x,\theta)$ 很難求嗎? 這似乎變成了一個雞生蛋蛋生雞的情況. (就我目前的理解) 所以通常 EM 處理的是 discrete 的 $z$, 然後利用 $\sum_z p(x,z|\theta)$ 算出 $p(x|\theta)$, 接著得到我們要的 $p(z|x,\theta)$. 等於是直接簡化了, 但 VI 無此限制.