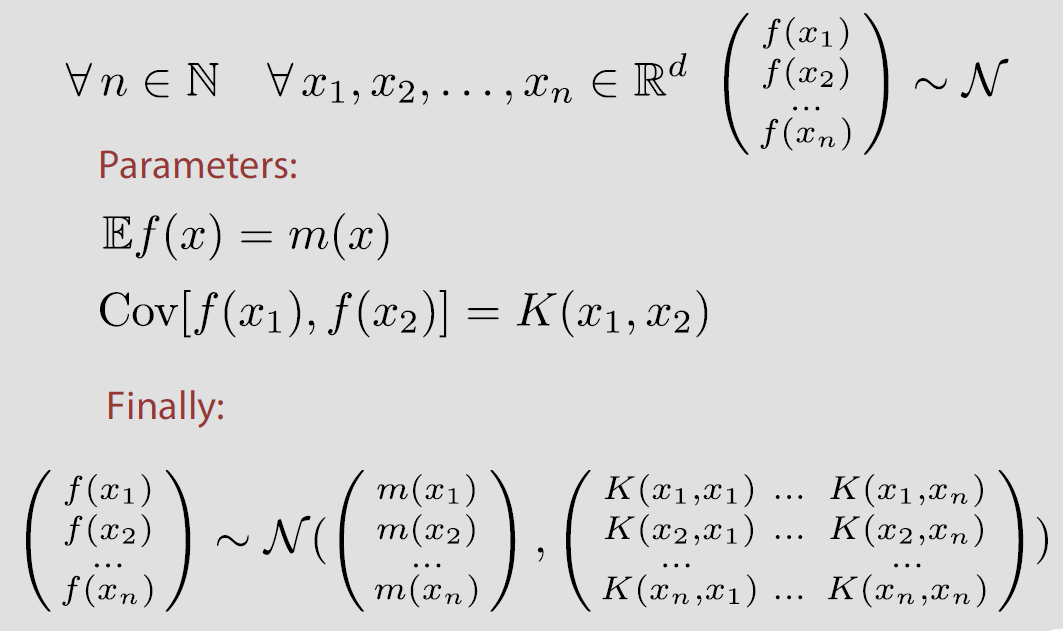Gaussian Process used in Bayesian Optimization

發表於 | 分類於 | [object Object]

上了 Coursera 的 Bayesian Methods for Machine Learning, 其中最後一週的課程介紹了 Gaussian processes & Bayesian optimization 覺得很有收穫, 因為做 ML 最痛苦的就是 hyper-parameter tuning, 常見的方法就是手動調, grid search or random search. 現在可以有一個較 “模型” 的作法: Bayesian optimization. 為了瞭解這個過程, 我們會介紹如下內容並同時使用 GPy and GPyOpt 做些 toy example:

  • Random Process and Gaussian Process
  • Stationary and Wide-Sense Stationary (WSS)
  • GP for regression
  • GP for bayesian optimization

讓我們進入 GP 的領域吧

Random Process (RP) and Gaussian Process (GP)

Random process (RP) 或稱 stochastic process 定義為

[Def]: For any $x\in\mathbb{R}^d$ assign random variable $f(x)$

例如 $d=1$ 且是離散的情形, ($x\in\mathbb{N}$) 定義說明對於每一個 $x$, $f[x]$ 都是一個 r.v. 所以 $f[1]$, $f[2]$, … 都是 r.v.s. 此 case 通常把 $x$ 當作時間 $t$ 來看.

而 Gaussian Process 定義為

[Def]: Random process $f$ is Gaussian, if for any finite number points, their joint distribution is normal.

Stationary and Wide-Sense Stationary (WSS)

Stationary

一個 RP 是 stationary 定義如下:

[Def]: Random process is stationary if its finite-dimensional distributions depend only on relative position of the points

簡單舉例: 取三個 r.v.s $(x_1,x_2,x_3)$ 他們的 joint pdf 會跟 $(x_1+t,x_2+t,x_3+t)$ 一模一樣
$$\begin{align} p(f(x_1),f(x_2),f(x_3))=p(f(x_1+t),f(x_2+t),f(x_3+t)) \end{align}$$
所以 pdf 只與相對位置有關, 白話講就是我們觀察 joint pdf 可以不用在意看的是哪個區段的信號, 因為都會一樣. 進一步地, 如果這個 RP 是 GP 的話, 我們知道 joint pdf 是 normal, 而 normal 只由 mean and variance totally 決定, 因此一個 GP 是 stationary 只要 mean and variance 只跟相對位置有關就會是 stationary. 基於這樣的條件我們可以寫出一個 stationary GP 的定義:

[Def]:

Covariance matrix or Kernel 只跟相對位置有關, 以下為三種常見的定義方式

不管怎樣, 通常相對位置近的 r.v. 都會假設比較相關, (這也符合實際狀況, 譬如聲音訊號時間點相近的 sample 會較相關), 也因此 kernel 都會長類似下面的樣子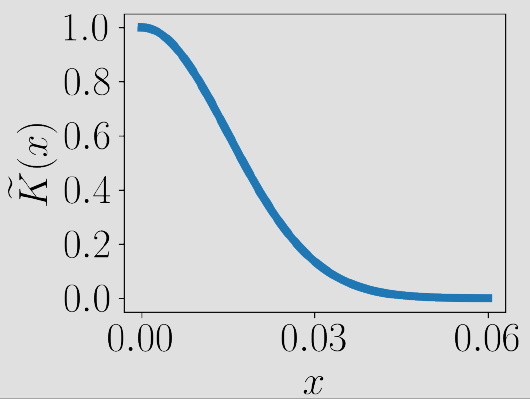

支線 Wide-Sense Stationary (WSS)

本段可跳過, 主要是為了更深地理解 stationary 做的補充.
WSS 定義為

[Def]: Random Process is WSS if its finite-dimensional distribution’s mean and variance depend only on relative position of the points

注意 WSS 與 Stationary 的定義差異. 準確來說 Stationary 要求所有的 moments 都只與相對位置有關, 但 WSS 只要求到 first and second order moments. 說明了 WSS 將 stationary 的條件放寬. 注意到 WSS 不一定是 stationary 的 GP, 這是因為 WSS 沒有要求 distribution 必須是 Normal.
WSS, Stationary GP, Stationary RP 之間的關係可以這麼描述:
$$\begin{align} \mbox{Stationary GP}\subset\mbox{Stationary RP}\subset\mbox{WSS} \end{align}$$

其實 WSS 與本篇主要討論的 Bayesian Optimization 沒有直接關係, 會想介紹是因為滿足 WSS 的話, 能使我們更直覺的 “看出” 一個訊號是否可能是 stationary. (另外 WSS 在 Adaptive Filtering 非常重要, 相當於基石的存在)
首先使用課程的 stationary 範例:

中間的圖明顯不是 stationary 因為 mean 隨著位置改變不是 constant, 但左邊和右邊就真的不是那麼容易看出來了. 那麼究竟有什麼方法輔助我們判斷 stationary 呢?
WSS 的 power-spectral density property 說明了一個 signal 如果是 WSS, 則它的 Covariance matrix or Kernel (訊號處理通常稱 auto-correlation) 的 DTFT 正好代表的物理意義就是 power spectral density, 而因為 kernel 不會因位置改變, 這導致了不管我們在哪個區段取出一個 window 的訊號, 它們的 power spectral density 都會長一樣. 這個性質可以讓我們很方便的 “看出” 是否是 stationary. (簡單講就是看 signal 的 frequency domain 是否因為隨著時間而變化, 變的話就一定不是 stationary)

好了, 接著回到主線去.

GP for regression

直接節錄課程 slides, 因為 stationary GP 的 mean 是 const, 因此我們扣掉 offset 讓其為 0, 之後再補回即可.
做 Regression 的目的就是 given $x$ 如何預測 $f(x)$, 而我們有的 training data 為 $x_1, …, x_n$ 以及它們相對的 $f(x_1),…,f(x_n)$. GP 就可以很漂亮地利用 conditional probability 預測 $f(x)$


由於是 GP, 導致上面藍色部分結果仍是 Gaussian, 因此我們得到
Regression 公式:

有時候我們的 observation $f(x)$ 是 noisy 的, 此時簡單地對 $f(x)$ 加上一個 random Gaussain noise 會使得我們的 model robust 些. 上面公式都不用改, 只要針對 kernel 作如下更動即可

GPy toolkit example

我們使用 Gaussian process regression tutorial 的範例, 使用上算是很直覺, 讓我們簡單實驗一下

1
2
3
4
5
6
7
8
9
10
11
12
13
import numpy as np
import GPy
import matplotlib.pyplot as plt
# Generate data points, where Y is noisy
X = np.random.uniform(-3.,3.,(20,1))
Y = np.sin(X) + np.random.randn(20,1)*0.2
# Define kernel, we use RBF
kernel = GPy.kern.RBF(input_dim=1, variance=1., lengthscale=1.)
# Define GP regression model
m = GPy.models.GPRegression(X,Y,kernel,noise_var=1.)
# See plot
fig = m.plot()
plt.show()

Codes 的結果如下

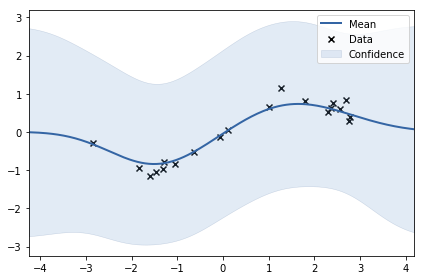
[Note]: 上圖的 Mean 和 Confidence 指的是 Regression 公式的 $\mu$ and $\sigma^2$ (前幾張有紅框的圖), 另外使用 GPy 算 regression 結果的話這麼使用

1
mu, sigma2 = m.predict(np.array([[1.0]]))

基本上 input 是一個 shape=(batch_size,in_dim) 的 array

可以看到就算是 data point 附近, 所顯示的 y 還是有非常大的 uncertainty, 這是因為 observation noise 的 variance 可能太大了, 我們從 1.0 改成 0.04 (正確答案) 看看

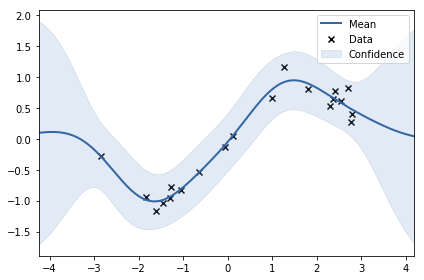
可以看到有 data point 的地方不確定性降低很多, 且不確定性看起來很合理 (當然, 因為我們用正確答案的 noise var)
接著我們改 kernel 的 lengthscale (控制平滑程度) 從 1 縮小成 0.5 應該可以預期 regression 的 mean 會扭曲比較大, 結果如下

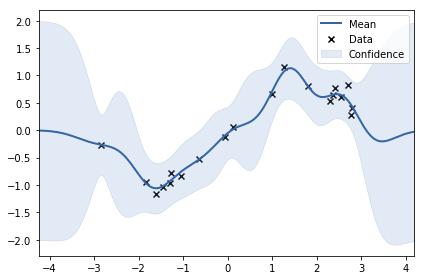
看看一個極端情況, 將 kernel 的 lengthscale 降到非常小, 這會導致 kernel 退化成 delta function, 也就是除了自己大家互不相關. 查看 regression 公式 (前幾張有紅框的圖), 由於 kernel 退化成 delta function, k 向量趨近於 0, 所以 regression 公式的 mean 趨近於 0, variance 趨近於 prior K(0). 我們將 lengthscale 調整成 0.02 得到如下的圖

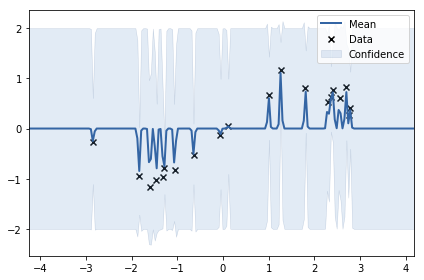
可以看到 x 稍微離開 data point 的地方, 基本 mean 就回到 0, 且 variance 回到 prior K(0)

從這簡單的實驗我們發現, 這三個控制參數:
-RBF variance
-RBF lengthscale
-GPRegression noise_var

設置不好, 基本很悲劇, 那怎麼才是對的? 下一段我們介紹使用最佳化方式找出最好的參數.

Learning the kernel parameters

由於都是 normal, 因此 MLE 目標函式可微, 可微就使用 gradient ascent 來求參數. 課程 slide 如下

GPy 的使用就這麼一行 m.optimize(messages=True)

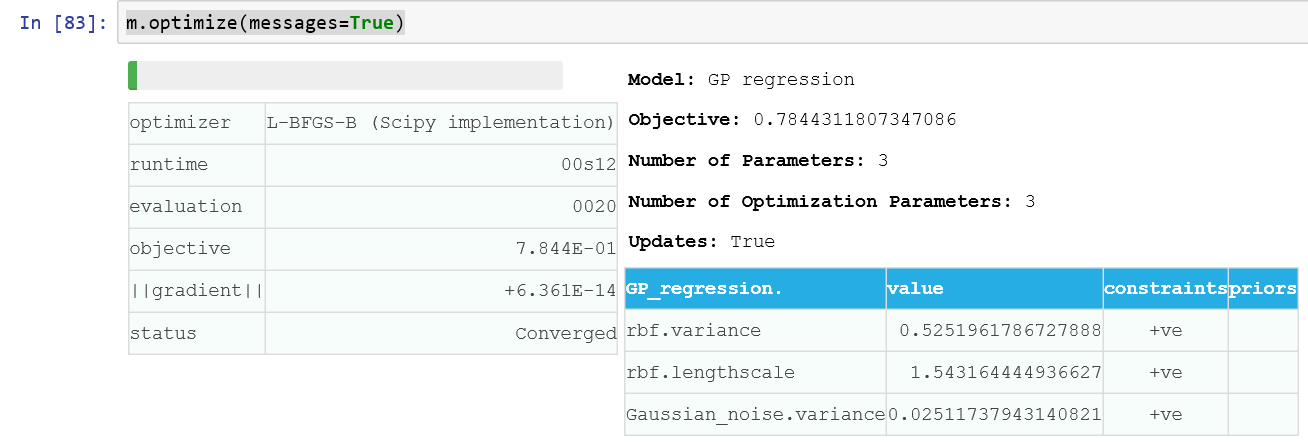
結果如下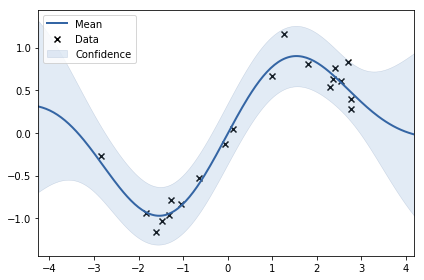

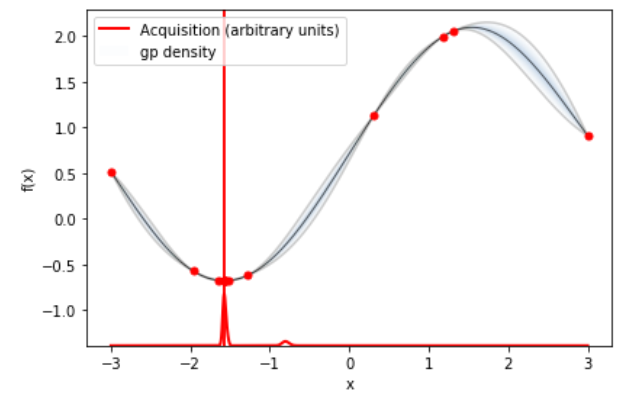
GP for bayesian optimization

問題再描述一下, 就是說模型有一大堆參數 (稱 $x$) 要調整, 選擇一組參數可以得到一個 validation accuracy (稱 $f(x)$), 我們希望找到一組參數使得 $f(x)$ 最大. 這個麻煩之處就在於我們對 $f(x)$ 的表示一無所知, 只能透過採樣得到 $f(x)$, 而每次要得到一個採樣的 $f(x)$ 都要經過漫長的訓練才能得到. 在這種情形下, 怎麼透過最少採樣點得到較大的 $f(x)$ 值呢?

大絕就是用 GP 來 approximate $f(x)$

合理嗎? 我們這麼想, 由於 kernel 一般的定義會使得相近的採樣點有較高的相關值, 也就是類似的參數會得到較相關的 validation accuracy. 這麼想的話多少有些合理. 另一個好處是使用 GP 可以帶給我們機率分布, 這使得我們可以使用各種考量來決定下一個採樣點. 例如: 我們可以考慮在那些不確定性較大的地方試試看, 因為說不定有更高的$f(x)$, 或是在已知目前估測的 GP model 下有較高的 mean 值那裏採樣. 這兩種方式稱為 “Exploration” and “Exploitation”

所以 Bayesian optimization 主要就兩個部分, Surrogate model (可以使用 GP) 和 Acquisition function:

演算法就很直覺了, 根據 Acquisition function 得到的採樣點 $x$ 計算出來 $f(x)$ 後, 重新更新 GP (使用 MLE 找出最好的 GP 參數更新), 更新後繼續計算下個採樣點. 我們還未說明 Acquisition function 怎麼定義, 常用的方法有下面三種:

  1. Maximum probability of improvement (MPI)
  2. Upper confidence bound (UCB)
  3. Expected improvement (EI), 網路上說最常被用

Expected improvement (EI) 可以參考這篇 blog 搭配這個 implementation, 這裡就不重複了. 值得一提的是 Acquisition function 通常有個參數 $\xi$ 可以控制 Exploration 和 Exploitation 的 tradeoff. 接著我們使用 GPyOpt 練習一個 toy example.

GPyOpt toy example

類似上面的 GP for regression 的範例, $x$ and $f(x)$ 我們簡單定義如下:

1
2
3
4
sample_num = 20
offset = 10
def probeY(x):	# i.e. f(x)
    return np.sin(x) + np.random.randn()*0.2 + offset

這次我們將 $f(x)$ 故意加了一個 offset, 雖然對於 GP regression 的假設是 mean=0, 不過 GPyOpt 預設會對 $f(x)$ 去掉 offset, 所以其實我們可以很安全的使用 API. 接著關鍵程式碼如下

1
2
3
4
5
6
7
8
bounds = [{'name': 'var_1', 'type': 'continuous', 'domain': (-3.0,3.0)}]  # domain definition
myBopt = GPyOpt.methods.BayesianOptimization(f=probeY,        # function to optimize       
                                             domain=bounds,   # box-constraints of the problem
                                             normalize_Y=True,      # normalize Y to mean = 0 (default)
                                             acquisition_type='EI', # acquisition function type (default)
                                             maximize=False,        # do maixmization? (default=False)
                                             exact_feval = False)
myBopt.run_optimization(max_iter)

bounds 描述了每一個 probeY 的 arguments. 特別要說一下 exact_feval = False, 這是說明 $f(x)$ 是 noisy 的, 所以會有 noise variance 可以 model (參考 3. GP for regression 的 regression 公式含noise的情形), 這在實際情況非常重要. 更多 BayesianOptimization 參數描述 參考這

使用如下指令看 acquisition 和 regression function 的結果

1
myBopt.plot_acquisition()

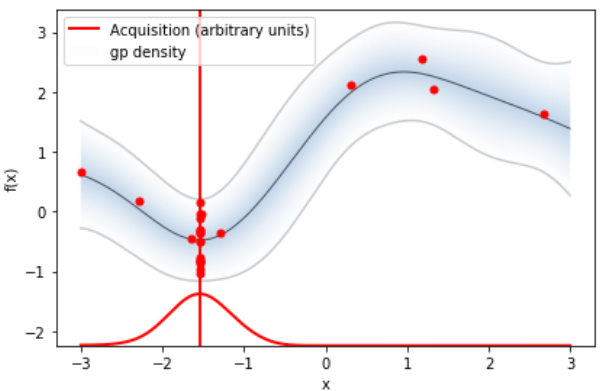
才花1x個採樣求出來的 regression function 就很逼近真實狀況了, 還不錯. 另外注意到這裡的 $f(x)$ 已經去掉 offset 了.
再來使用如下指令看每一次採樣值之間的差異, 以及採樣點的 $f(x)$

1
myBopt.plot_convergence()

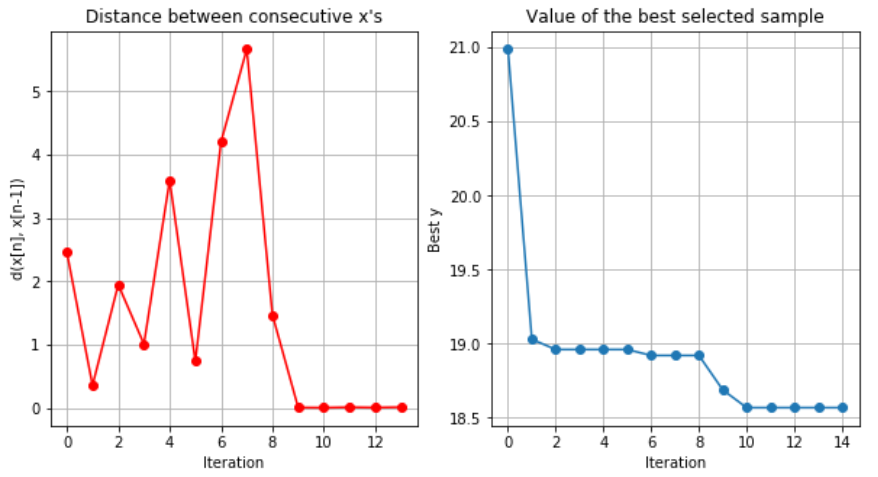
第9次採樣開始, 採樣點 $x$ 以及 $f(x)$ 之間基本沒什麼差異了.
若要拿到採樣過程的 $x$ and $f(x)$, 可使用 myBopt.X 和 myBopt.Y

XGBoost parameter tuning

針對 XGBoost 的參數進行最佳化 (可參考這篇 blog), 關鍵就在於上面的 $probeY$ 需替換成計算某個採樣的 evaluation accuracy (因此還需要訓練). 關鍵程式碼如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
from xgboost import XGBRegressor
from sklearn.model_selection import cross_val_score
... Some codes here
# Score. Optimizer will try to find minimum, so we will add a "-" sign.
def probeY(parameters):
    parameters = parameters[0]
    score = -cross_val_score(
                XGBRegressor(learning_rate=parameters[0],
                              max_depth=int(parameters[2]),
                              n_estimators=int(parameters[3]),
                              gamma=int(parameters[1]),
                              min_child_weight = parameters[4]), 
                X, y, scoring='neg_mean_squared_error').mean()
    score = np.array(score)
    return score
# Bounds (NOTE: define continuous variables first, then discrete!)
bounds = [
            {'name': 'learning_rate', 'type': 'continuous', 'domain': (0, 1)},
            {'name': 'gamma', 'type': 'continuous', 'domain': (0, 5)},
            {'name': 'max_depth', 'type': 'discrete', 'domain': (1, 50)},
            {'name': 'n_estimators', 'type': 'discrete', 'domain': (1, 300)},
            {'name': 'min_child_weight', 'type': 'discrete', 'domain': (1, 10)}
         ]
np.random.seed(777)
optimizer = GPyOpt.methods.BayesianOptimization(f=f, domain=bounds,
                                                acquisition_type ='MPI',
                                                acquisition_par = 0.1,
                                                exact_eval=True)
max_iter = 50
max_time = 60
optimizer.run_optimization(max_iter, max_time)
optimizer.plot_convergence()
optimizer.X[np.argmin(optimizer.Y)]

課程讓我們測試了 sklearn.datasets.load_diabetes() dataset, 使用 GPyOpt 可以讓 XGBoost 比預設參數有 9% 的提升! 還是很不錯的.

再來就很期待是否能真的在工作上對 DNN 套用了.

Reference

  1. GPy and GPyOpt
  2. GPyOpt’s documentation can find APIs
  3. GPyOpt tutorial
  4. 很好的 GPy and GPyOpt 數學和範例 blog
  5. Acquisition function implementation
  6. WSS power-spectral density property https://www.imft.fr/IMG/pdf/psdtheory.pdf