這是 far field 筆記系列第一篇, 主要為自己學習用, 如有錯誤還請指正. 主要參考 Optimum Array Processing Ch2 以及 Microphone Array Signal Processing Ch3.
Beampattern 就是希望能得到如下圖 [ref Fig3.3] 的表示, 說明經過一個麥克風陣列的處理後, 每個角度所得到的增益情形. 因此可以看出主要保留哪些方向的訊號, 以及抑制哪些方向的訊號.

Geometry Settings
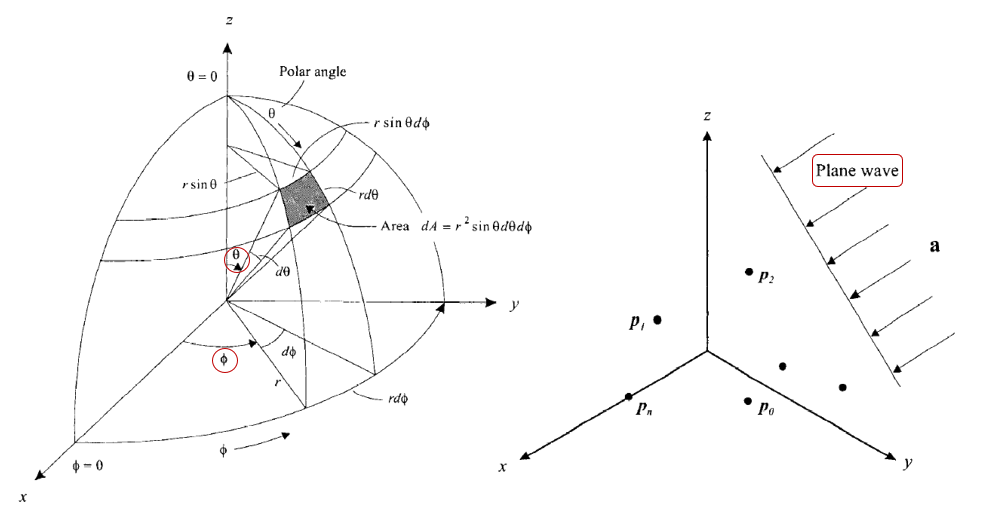
遠場一般假設 plan wave, 和 narrow band. 實際處理語音等 broadband 時我們會採取 fft 分頻. 我們定義如下的 geometry, 其中重要的兩個角度為 $\theta$ 和 $\phi$ (如圖紅圈). $\mathbf{a}$ 表示聲源的入射單位向量. 以下符號如果是粗體表示為向量或矩陣, 否則就是 scalar.
Signal Model
我們定義 $f(t)$ 為聲源訊號, $v_n(t)$ 為 nth mic 的噪聲源
Anechoic Model

我們以下的介紹都是基於 Anechoic Model, 並且先做如下的簡化
Reverberant Model

相當於將 attenuation factor $\alpha$ 改成 impulse response, 所以相乘改成 convolution.
Time Delay
為了方便推導麥克風之間的 time delay, 我們先將 Anechoic Model 做如下簡化
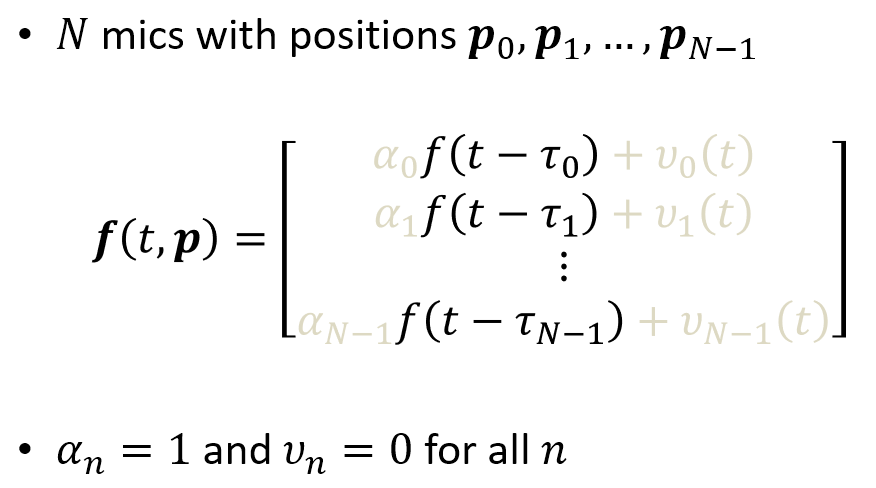
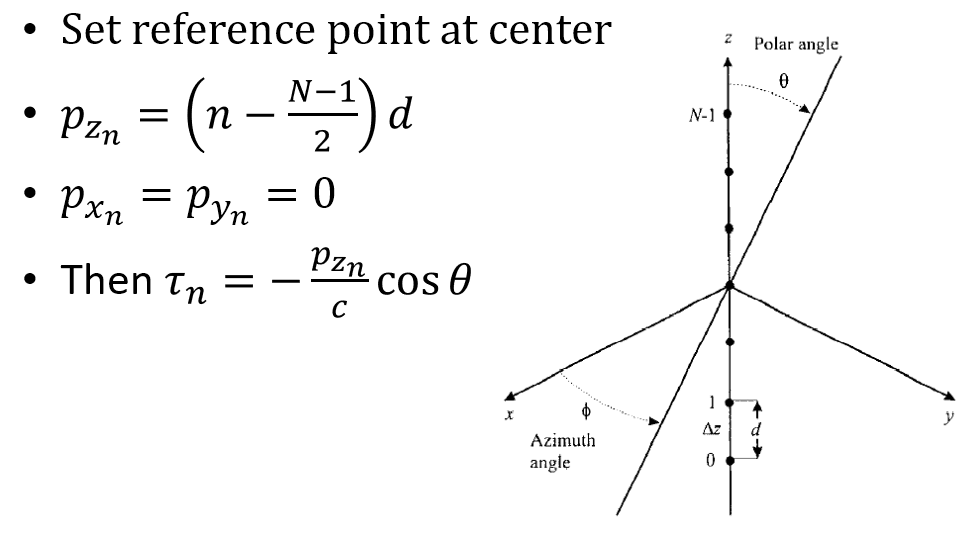
因此對於 plan wave 假設和聲源的入射單位向量 $a$ 來說, 我們很容易就得到 time delay 如下

Uniform Lineary Array (ULA)
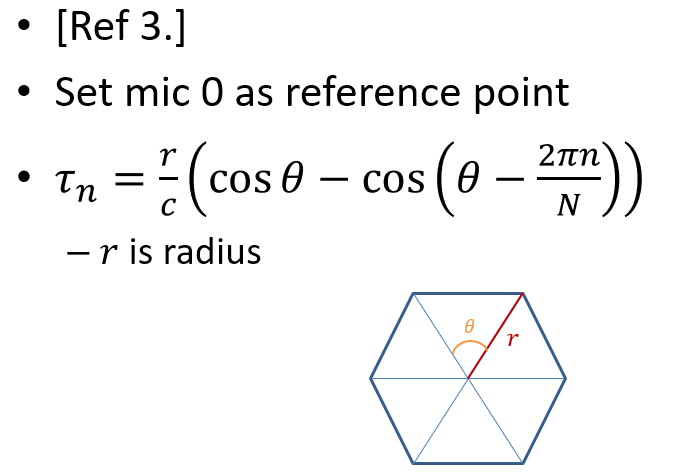
Circular Array
以一個 6 mic 的 circular array 來說, 有如下的 time delay
Array Manifold Vector
由於 time delay $\tau$ 在 freqeuncy $\omega$ 只是乘上 $e^{-j\omega\tau}$, 因此我們可以得到一個 compact 的表示

重複一遍這裡得到的重要式子
$$\begin{align} \color{red}{ \mathbf{F}(\omega,\mathbf{p})=F(\omega)\mathbf{\upsilon}_k(\mathbf{k}) } \end{align}$$我們稱 $\mathbf{\upsilon}_k(\mathbf{k})$ 為 Array Manifold Vector.
要注意的是, 其實也可以用 time delay $\tau$ 來表示, 這時我們這麼寫 (如上圖灰色的部分)
$$\mathbf{\upsilon}_\tau (\mathbf{\tau})= \left[ \begin{array}{clr} e^{-j\omega\tau_0} \\ e^{-j\omega\tau_1} \\ \vdots \\ e^{-j\omega\tau_{N-1}} \end{array} \right]$$
或甚至入射角度 $\theta$ 如果可以完全表達 $\tau$ 的話, 我們也能這麼寫 $\mathbf{\upsilon}_\theta(\mathbf{\theta})$.
Array Signal Processing
早期的 array processing (narrow band) 是對每個麥克風有各自的 weights, 然後再總合起來, 這種作法叫做 weight-and-sum. 而對於 broadband 訊號來說, 相當於拆頻乘很多 narrow band, 因此在每個頻帶上, 都有 N 個麥克風的 weights. 這在時域上等價於每個麥克風都有各自的 filters, 稱 filter-and-sum. 以下介紹 filter-and-sum 和頻域的架構.
Filter-and-Sum
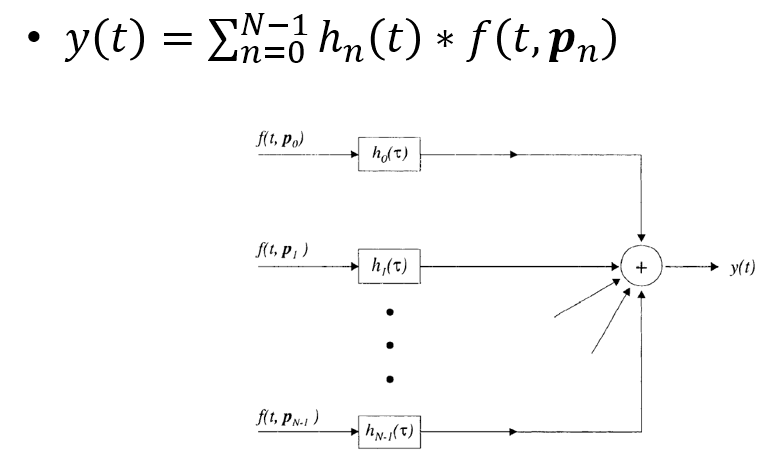
在實作上通常採用 FIR filter, 因此架構如下:
符號有點不同, 這是因為圖是採用另一本書 Microphone Array Signal Processing
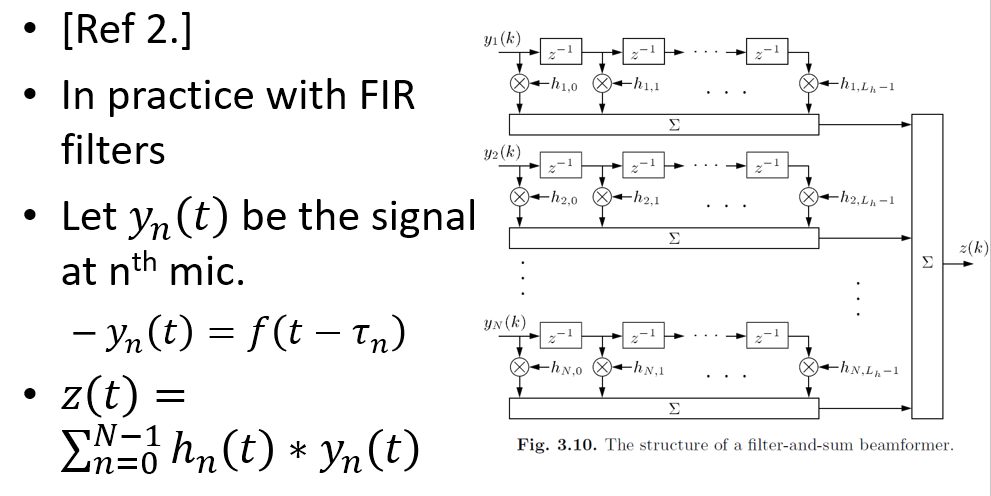
Frequency Domain
針對 filter-and-sum 做 frequency transform 得到如下:

實際架構圖如下:
一樣符號有點不同, 這是因為圖是採用另一本書 Microphone Array Signal Processing

Frequency-wavenumber Response Function
針對 frequency domain 的 array processing, 我們可以帶入先前推得的 (1) 得到如下:
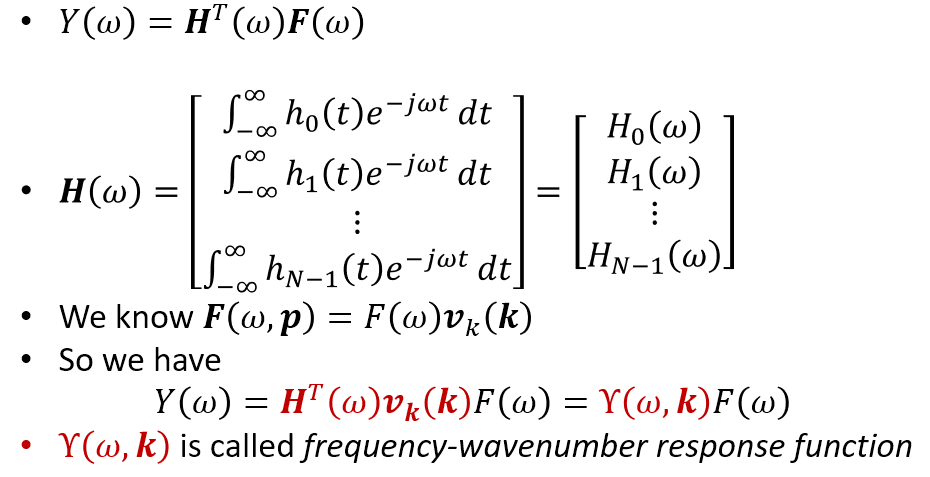
所以 $\Upsilon(\omega,\mathbf{k})$ 物理意義就是針對 frequency $\omega$ 和 wavenumber $\mathbf{k}$ (控制了聲源入射角度 $\theta$ 等等的物理量) 的 response.
Beampattern
wavenumber $\mathbf{k}$ 比較抽象, 如果我們換成角度 $\theta$, $\phi$ 就會直觀很多, 而 beampattern 只是針對 $\Upsilon(\omega,\mathbf{k})$ 換成用角度而已.
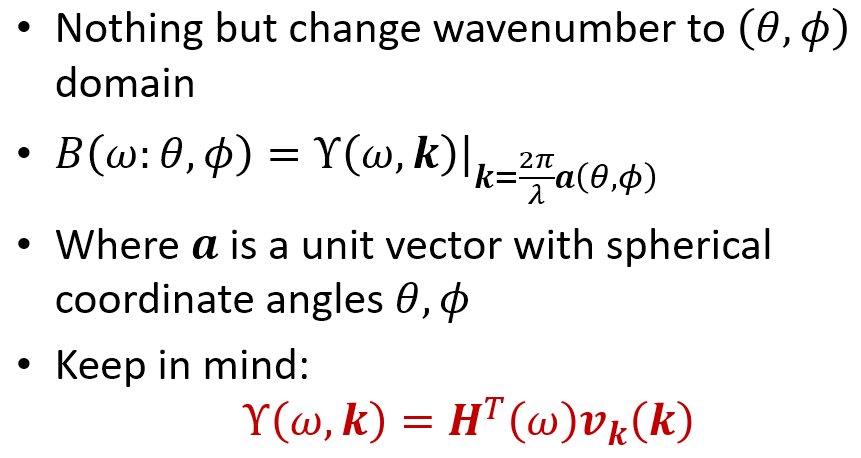
所以 $B(\omega:\theta,\phi)$ 物理意義就是針對 frequency $\omega$ 和入射角度 $\theta$, $\phi$ 的 response.
Delay-and-sum Beampattern
Delay-and-sum 想法很簡單, 就是補償每個 mic 的 time delay 而已. 因此所需要的 filter $H(\omega)$ 就是 array manifold vector 的 conjugate 即可. 如下圖:
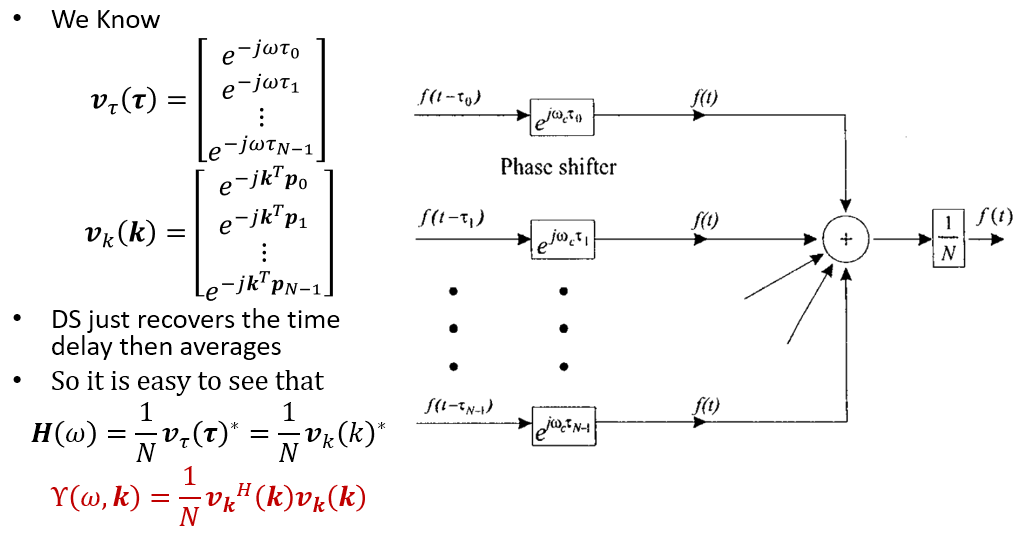
但這麼做有個缺點, 就是高頻時雖然針對聲源方向的 mainlobe 變窄了, 但同時 sidelobe 卻變多了. 也就是在高頻時, 某些方向的聲源消不掉. 如下圖:
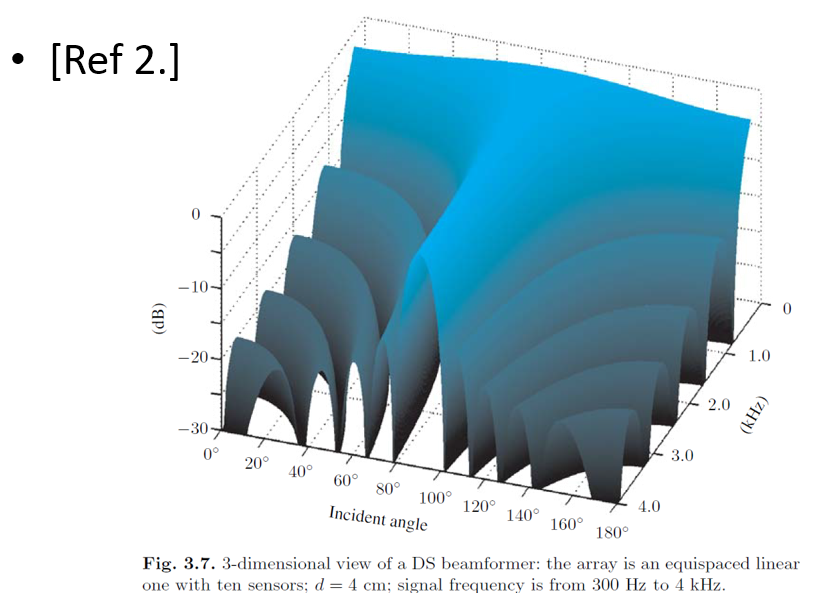
Fixed Beampattern
為了修正上述 DS beamformer 的問題, 我們希望得到 response-invariant broadband beamformer. 希望能有下圖的結果:

中心思想很簡單, 針對某個頻率 $\omega$ 來求出相對應的 $H$ 使得 beampattern 會與我們 desired beampattern 有 least-sqaure 差異. 以下 $H(\omega)$ 會省略 $\omega$ 不寫


結論
到這裡我們討論了遠場的 signal model, 針對 anechoic model 我們最終導出了 beampattern. 做為例子我們使用簡單的 delay-and-sum (DS) beamformer 來看它的 beampattern 長什麼樣. 可以看到在高頻時很多方向還是無法壓抑, 因此使用 least-square 方法找出每個頻率需要的 spatial filter 來逼近我們需要的 beampattern.