Far Field Notes (2) LCMV filter and Frost's algorithm

發表於 | 分類於 | [object Object]

這是 far field 筆記系列第二篇, 主要為自己學習用, 如有錯誤還請指正. 主要參考 Microphone Array Signal Processing Ch4 和 Frost’s algorithm

上一篇最後雖然使用 fixed beamformer 得到了 response-invariant beamformer, 但這個方法限制是 filter 一旦設計好就寫死了, 沒辦法自己 update (所以才叫 “fixed” beamformer). 這引入一個問題是, 如果剛好有一個 inteference noise 在衰減不那麼大的角度時, 就無法壓得很好. 而這篇要介紹的 LCMV (Linear Constrained minimum variance) filter 以及 Frost’s beamformer 能針對給定的方向抽取訊號, 並且對其他方向的 inteference nosie 壓抑的最好. 注意 sound source 方向必須給定, LCMV 求得的 weights 會想辦法對其他方向的 inteference 壓抑.

如同 LCMV 字面上的意思一樣. 會將整個問題轉換成 minimize variance subject to some linear constraints. 另外相當經典的 Frost’s beamformer (1972年呢!) 則將 filter 的 optimal 求解改成使用 stochastic gradient descent 方式, 所以非常適合實際的 real time 系統, 這些下文會詳細說明.

架構設定和 Signal Model

架構如下圖 (圖片來源:ref), 第一步是一個 delay stage, 這相當於是針對一個 steering direction 補償每個 mic 之間的 time delay (訊號對齊好). 第二步才是 beamformer, 我們知道 time domain 使用 filter-and-sum 架構, 如果是 frequency domain 則使用拆頻的架構. 忘了可參考第一篇.

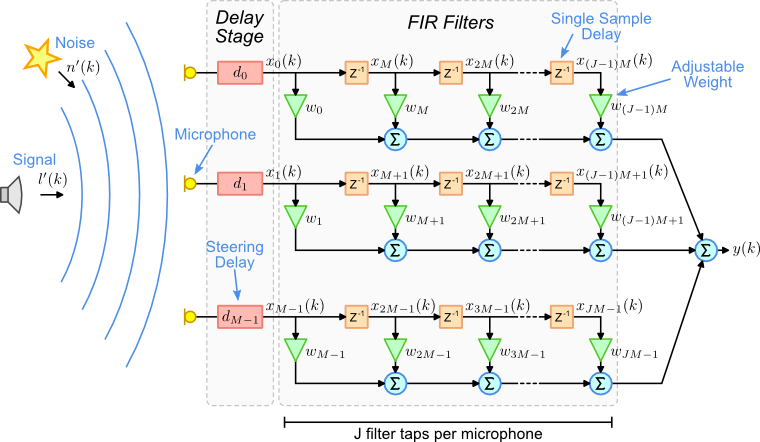
本文以 filter-and-sum 來筆記, 另外 signal model 以下推導將會使用 anechoic model, 第一篇有定義可回去查閱. 同時本文接下來的 notation 會與圖中的不同. 上圖只是用來顯示 filter-and-sum 架構.

Notations

一些 notations 我們先定義起來. $N$ 是麥克風數量, $L$ 是 filter tap 數量, 我們 aligned 好的 anechoic model 如下:
$$\begin{align} \mathbf{y}(k)=s(k)\mathbf{\alpha}+\mathbf{v}(k) \end{align}$$其中
$$\begin{align} \mathbf{y}(k)=[y_1(k),...,y_N(k)]^T \\ \mathbf{v}(k)=[v_1(k),...,v_N(k)]^T \\ \mathbf{\alpha}=[\alpha_1,\alpha_2,...,\alpha_N]^T \end{align}$$ $s(k)$ 是時間 $k$ 的聲源訊號, $\alpha$ 是 $N\times 1$ 的 attenuation factors, $\mathbf{v}(k)$ 是時間 $k$ 的 $N\times 1$ noise 訊號向量, 因此 $\mathbf{y}(k)$ 是時間 $k$ 的 $N\times 1$ 麥克風收到的訊號向量. 注意到由於我們先 align 好 delay 了, 所以原先的 anechoic model 可以簡化成上面的表達.

考慮到 filter-and-sum 架構, 我們將整個 $N$ 個 mic 每個 mic 都有 $L$ 個值以下圖(圖片來源:ref)的順序串成一個 $NL$ vector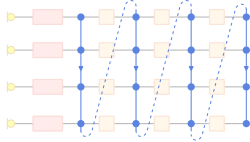

因此我們得到這些向量
$$\begin{align} \mathbf{y}_{NL}(k)=[\mathbf{y}^T(k), \mathbf{y}^T(k-1), ..., \mathbf{y}^T(k-L+1)]^T \\ \mathbf{x}_{NL}(k)=[s(k)\mathbf{\alpha}^T, s(k-1)\mathbf{\alpha}^T, ..., s(k-L+1)\mathbf{\alpha}^T]^T \\ \mathbf{v}_{NL}(k)=[\mathbf{v}^T(k), \mathbf{v}^T(k-1), \mathbf{v}^T(k-L+1)]^T \end{align}$$所以整體的 signal model 改寫 (1) 後可得:
$$\begin{align} \mathbf{y}_{NL}(k)=\mathbf{x}_{NL}(k) + \mathbf{v}_{NL}(k) \end{align}$$

Filter-and-sum 的 filter $\mathbf{h}$ 也用這個順序定義如下, 因此是一個長度為 $NL$ 的向量
$$\begin{align} \mathbf{h}=[\mathbf{h}_0^T, \mathbf{h}_1^T, \mathbf{h}_{L-1}^T]^T \end{align}$$
最後整個 beamformer 的輸出 $z(k)$ 就可以這麼寫
$$\begin{align} z(k)=\mathbf{h}^T\mathbf{y}_{NL}(k) = \color{orange}{ \mathbf{h}^T\mathbf{x}_{NL}(k) } + \color{blue}{ \mathbf{h}^T\mathbf{v}_{NL}(k) } \end{align}$$

Problem Definition

LCMV 的主要想法就圍繞在 (10) 的橘色和藍色兩個部分上面: 我們希望橘色部分能夠還原出原始訊號 $s(k)$ 且藍色部分能夠愈小愈好 (代表著 noise 愈小愈好).

  1. 首先我們將橘色部分作如下推導:

    $$\begin{align} \color{orange}{ \mathbf{h}^T\mathbf{x}_{NL}(k) } =\mathbf{h}^T \left[ \begin{array}{clr} s(k)\mathbf{\alpha} \\ s(k-1)\mathbf{\alpha} \\ \vdots \\ s(k-L+1)\mathbf{\alpha} \end{array} \right] = sum\left( \left[ \begin{array}{clr} \mathbf{h}_0^T\mathbf{\alpha}\cdot s(k) \\ \mathbf{h}_1^T\mathbf{\alpha}\cdot s(k-1) \\ \vdots \\ \mathbf{h}_{L-1}^T\mathbf{\alpha}\cdot s(k-L+1) \end{array} \right] \right) \\ = sum\left( \color{red}{ \left[ \begin{array}{clr} u_0\cdot s(k) \\ u_1\cdot s(k-1) \\ \vdots \\ u_{L-1}\cdot s(k-L+1) \end{array} \right] } \right) \end{align}$$

    (12) 為引入的條件, 藉由這樣的條件來還原原始訊號.
    $u$ ($L$長度的向量) 定義了我們希望在時間 $k$ 的還原結果, 是原始訊號的權重和
    定義一個 matrix (size of $NL\times L$) 如下:

    $$\begin{align} \mathbf{C}_{\mathbf{\alpha}}= \left[ \begin{array}{clr} \mathbf{\alpha} & \mathbf{0} & \cdots & \mathbf{0} \\ \mathbf{0} & \mathbf{\alpha} & \cdots & \mathbf{0} \\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{0} & \mathbf{0} & \cdots & \mathbf{\alpha} \\ \end{array} \right] = \left[ \begin{array}{clr} \mathbf{c}_{\alpha,0} & \mathbf{c}_{\alpha,1} & \cdots & \mathbf{c}_{\alpha,L-1} \\ \end{array} \right] \end{align}$$

    觀察 (11) and (12) 並利用 $\mathbf{C_{\alpha}}$ 可以將 constraint 明確寫出如下:

    $$\begin{align} \mathbf{C_{\alpha}}^T\mathbf{h}=\mathbf{\mathbf{u}} \end{align}$$

  2. 藍色部分代表最後的 noise 成分, 希望愈小愈好
    計算藍色部分的能量為

    $$\begin{align} \mathbf{h}^T \mathbb{E} \left[ \mathbf{v}_{NL}(k)\mathbf{v}_{NL}^T(k) \right] \mathbf{h}=\mathbf{h}^T\mathbf{R}_{\mathbf{v},\mathbf{v}}\mathbf{h} \end{align}$$

    但關鍵是我們無法得知實際的 noise signal, 我們有的只有 observation $\mathbf{y}_{NL}(k)$, 那該怎麼辦呢?
    LCMV 很厲害的一點是, 由於上面剛提到的 constraints, 導致橘色部分的能量是 constant, 因此以下兩個問題是等價的

    $$\begin{align} \min_{\mathbf{h}}{ \mathbf{h}^T\mathbf{R}_{\mathbf{v},\mathbf{v}}\mathbf{h} } \equiv \min_{\mathbf{h}}{ \mathbf{h}^T\mathbf{R}_{\mathbf{y},\mathbf{y}}\mathbf{h} } \end{align}$$

到這裡我們可以寫出完整的最佳化問題
$$\begin{align} \begin{array}{clr} \color{blue}{ \min_{\mathbf{h}}{ \mathbf{h}^T\mathbf{R}_{\mathbf{y},\mathbf{y}}\mathbf{h} } } \\ \color{orange}{ \mbox{subject to }\mathbf{C_{\alpha}}^T\mathbf{h}=\mathbf{\mathbf{u}} } \end{array} \end{align}$$

Optimal Solution

要解問題 (17), 基本上使用 Lagrange function 求解就可以, 解如下:
$$\begin{align} \mathbf{h}=\mathbf{R}_{\mathbf{y},\mathbf{y}}^{-1}\mathbf{C_{\alpha}} \left( \mathbf{C_{\alpha}}^T \mathbf{R}_{\mathbf{y},\mathbf{y}}^{-1} \mathbf{C_{\alpha}} \right)^{-1} \mathbf{u} \end{align}$$

但是重點來了, 以上這些推導全部都假設是 stationary, 實際情況一定是 non-stationary 怎麼辦? 最直覺的想法就是, 我們每隔一段時間就用 (18) 重新算一下 $\mathbf{h}$. 但很明顯這非常沒效率 (covariance估計, inverse運算) 根本不可行. 因此必須改成 iteratively update $\mathbf{h}$ 的方式.
Frost’s algorithm 的一個重要貢獻也就是在這, 使用 stochastic gradient descent 方式 update $\mathbf{h}$!

Frost’s Algorithm

問題 (17) 的 Lagrange function 如下:
$$\begin{align} \mathcal{L}(\mathbf{h},\mathbf{\lambda}) = \frac{1}{2} \mathbf{h}^T\mathbf{R}_{\mathbf{y},\mathbf{y}}\mathbf{h} + \mathbf{\lambda}^T(\mathbf{C_{\alpha}}^T\mathbf{h}-\mathbf{\mathbf{u}}) \end{align}$$因此 gradient 如下:
$$\begin{align} \nabla_{\mathbf{h}}\mathcal{L} = \mathbf{R}_{\mathbf{y},\mathbf{y}}\mathbf{h} + \mathbf{C_{\alpha}}\mathbf{\lambda} \end{align}$$gradient descent update 式子如下:
$$\begin{align} \mathbf{h}_{t+1} = \mathbf{h}_{t} - \mu \left( \mathbf{R}_{\mathbf{y},\mathbf{y}}\mathbf{h}_t + \mathbf{C_{\alpha}}\mathbf{\lambda}_t \right) \end{align}$$由於有 constraint, 必須滿足 update 後仍然滿足條件, 因此:
$$\begin{align} \mathbf{u}=\mathbf{C_{\alpha}}^T\mathbf{h}_{t+1} \end{align}$$將(21)帶入(22)整理得到$\lambda_t$, 接著再將$\lambda_t$帶回(21)得到結果如下, 並不困難只是一些代數運算:
$$\begin{align} \mathbf{h}_{t+1} = \mathbf{h}_{t} - \mu \left[ \mathbf{I} - \mathbf{C}(\mathbf{C}^T\mathbf{C})^{-1}\mathbf{C}^T \right] \mathbf{R}_{\mathbf{y},\mathbf{y}} \mathbf{h}_{t} + \mathbf{C}(\mathbf{C}^T\mathbf{C})^{-1} \left[ \mathbf{u}-\mathbf{C}^T\mathbf{h}_t \right] \end{align}$$定義兩個 matrix $\mathbf{A}$, $\mathbf{B}$ 如下 (注意到這兩個 matrix 是事先計算好的):
$$\begin{align} \mathbf{A} \triangleq \mathbf{C}(\mathbf{C}^T\mathbf{C})^{-1}\mathbf{u} \\ \mathbf{B} \triangleq \mathbf{I} - \mathbf{C}(\mathbf{C}^T\mathbf{C})^{-1}\mathbf{C}^T \end{align}$$因此可以改寫(23)如下:
$$\begin{align} \mathbf{h}_{t+1} = \mathbf{B}[\mathbf{h}_t - \mu \mathbf{R}_{\mathbf{y},\mathbf{y}} \mathbf{h}_t] + \mathbf{A} \end{align}$$由於使用 stochastic 方式, 因此 expectation 使用最新的一次 sample 即可:
$$\begin{align} \mathbf{R}_{\mathbf{y},\mathbf{y}} = \mathbb{E} \left[ \mathbf{y}_{NL}(t)\mathbf{y}_{NL}^T(t) \right] \thickapprox \color{green}{ \mathbf{y}_{NL}(t)\mathbf{y}_{NL}^T(t) } \end{align}$$將(27)帶入(26)並用(10)替換一下, 我們得到最終的 update 式子:
$$\begin{align} \color{red}{ \mathbf{h}_{t+1} = \mathbf{B}[\mathbf{h}_t - \mu z(t)\mathbf{y}_{NL}(t)] + \mathbf{A} } \end{align}$$由於 $\mathbf{A}$ 和 $\mathbf{B}$ 是固定的, 跟原來的 optimal 解比較 (18), 可以明顯知道速度上會快非常多.
另外 $\mathbf{h}_0$ 只需要選擇一個 trivial 的 feasible point 即可:
$$\begin{align} \mathbf{h}_{0} = \mathbf{A} \end{align}$$

結論

本篇記錄了 filter-and-sum 架構的 beamformer, LCMV 的問題和其最佳解. LCMV 可以針對給定的一個方向, 找出 filter $\mathbf{h}$ 使得抽取看的方向的訊號同時壓抑其他方向的訊號.
實作上直接套用最佳解太慢不可行, 而 Frost’s algorithm 提供了一個 stochastic gradeint update 方法更新 $\mathbf{h}$, 這使得 real-time system 變得可行.

Reference

  1. Microphone Array Signal Processing by Jocab Benesty
  2. Frost’s algorithm