粗略筆記 time domain adaptive filters, frequency domain adaptive filters 會在下一篇筆記. 應用以 Acoustic Echo Cancellation (AEC) 來說明.
Motivation
直接使用 wiki. AEC 要解決的是如下的情形
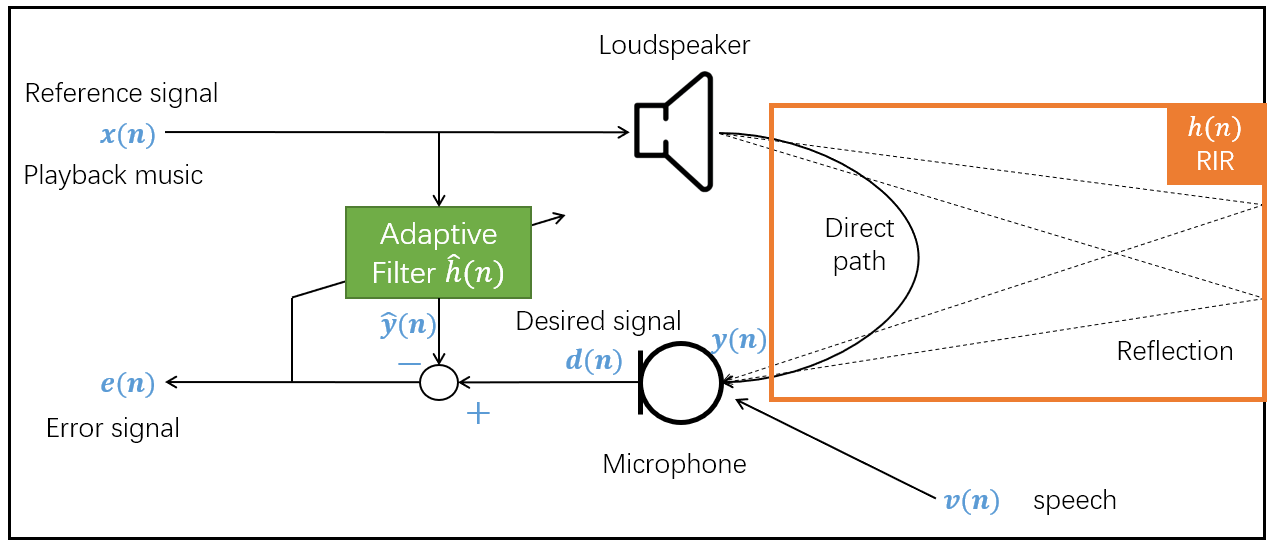
各個訊號關聯如下:
$$\begin{align} y(n)=h(n)\ast x(n) \\ d(n)=y(n)+v(n) \\ \hat{y}(n)=\hat{h}(n)\ast x(n)\\ e(n)=d(n)-\hat{y}(n) \end{align}$$目的是找到 $\hat{h}$ 滿足下式:
$$\begin{align} \hat{y}(n)\approx y(n)\Rightarrow e(n)\approx v(n) \end{align}$$ 對於第 $n$ 個 sample 點來說, 我們通常使用過去(含自己) $p$ 個 samples. 下面小寫粗體表示 vector, 大寫粗體表示 matrix.
Optimal Solution
也就是 Wiener solution.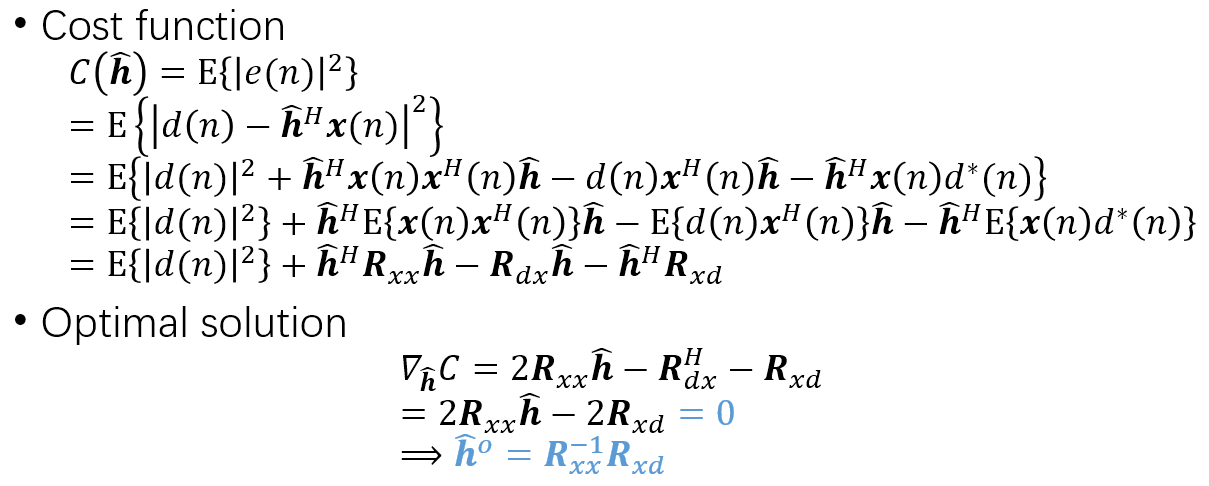
但在真實世界中, 不管 reference signal ($x(n)$) or desired signal ($d(n)$) 都是 non-stationary 的. 最直接且暴力的想法就是每隔一段時間重新算一次 Wiener solution. 不過想當然爾這是行不通的. 因此就必須採用 Stochastic update 方式.
Stochastic Update
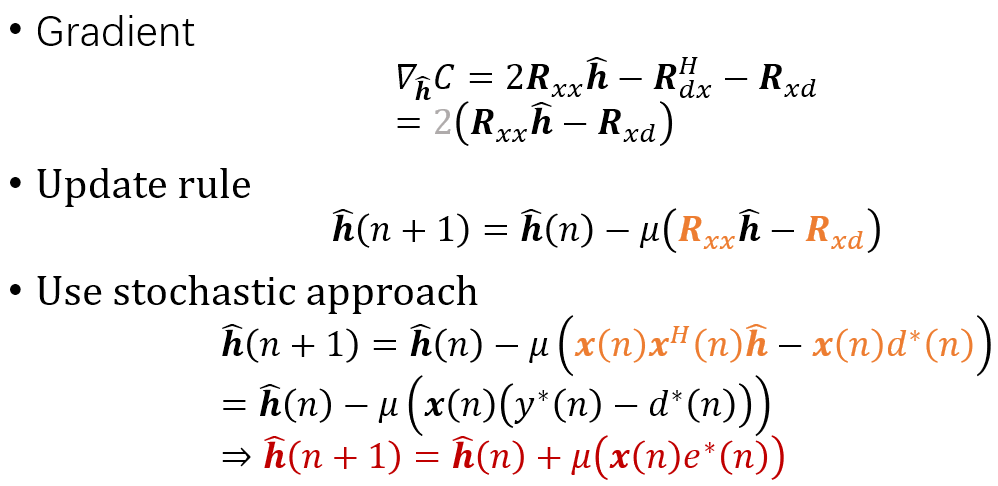
上面紅色的式子就是典型的 LMS algorithm.
另外我們知道 optimization 還可以使用 second-moment, 也就是使用二階導函數 (Hessian Matrix). 這就是 Newton’s method:
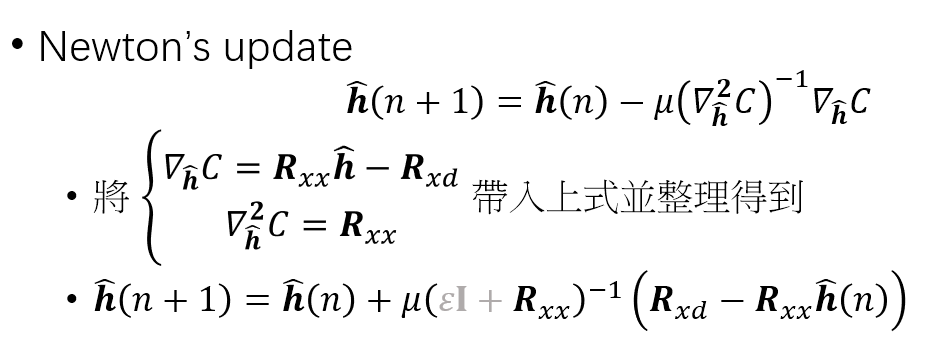
針對 $\mathbf{R}_{xx} \mbox{ , } \mathbf{R}_{xd}$ 使用不同的 approximation 方式就會得到不同演算法, 例如:
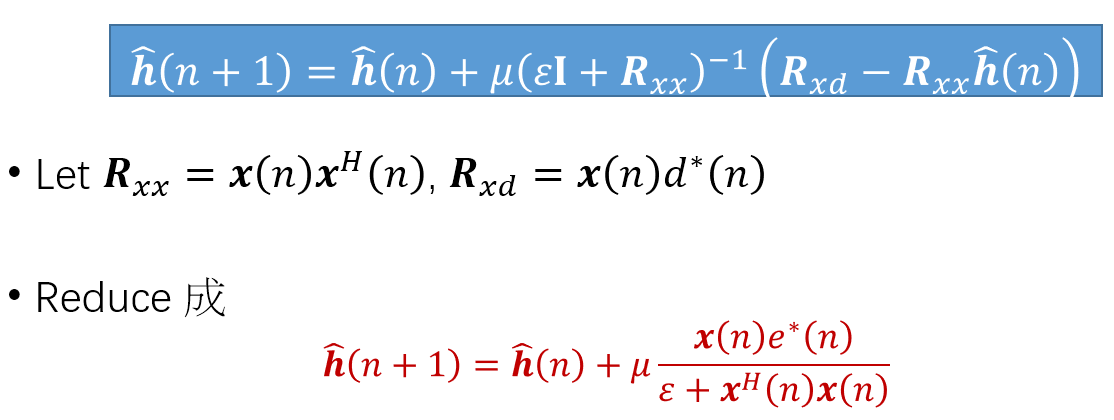
上面紅色的式子就是典型的 NLMS algorithm.
用這樣的方式還可推出 e-NLMS, leaky-LMS, RLS 等等…
實作上 NLMS 在 reference signal $x(n)$ 很小的時候, 由於公式上分母會除以 $x^Hx$, 而分子只有一次方 $x$, 因此除下來會導致 gradient 容易變大, 所以發散. 這是 NLMS 實作上要考慮的情形.
Misadjustment
我們知道最佳解為 Wiener solution, 但由於我們採用 stochastic gradient 方式, 也就是說 update 的 gradient 本身存在誤差, 這些 gradient 的 variance 就直接影響了最終收斂的效果跟 Wiener solution 的收斂結果之間的差距. 此差距我們稱 misadjustment 或稱 Excess Meam Square Error
直接擷取 Ali Sayed, Adaptive Filters p230 的定義:

為什麼要說這個呢? 是因為實作上有兩個因素會直接影響最終收斂效果的好壞, 分別是 tap length 和 step size. 從理論分析和實作經驗來說, tap length 太小會無法有效模擬 RIR, 而太大會導致 EMSE 提高 (收斂效果反而變差), 因此選取的 tap length 必須要根據 sampling rate 和要消除的 echo path 來計算一下.
LMS or NLMS 的 EMSE 可猜考 Ali Sayed, Adaptive Filters p249 and p253. (條件已簡化在 ref and desired signals 為 stationary 情況)
另外 step size 較小會有較好的收斂效果, 但是收斂速度會慢且 tracking 能力較差. 一個有效的方式為使用 Practical Variable Step Size (PVSS) 方法, 具體可參考 待補
好了, time domain 到這就差不多了, 缺點也很明顯, 慢!, 因為是 sample-by-sample 處理. 接著稍微梳理一下 frequency domain 方法.