Adaptive Filters 簡介 (2) Fast Convolution and Frequency Domain

上一篇說明了 time domain 的 adaptive filters, 由於是 sample-by-sample 處理, 因此太慢了不可用, 真正可用的都是基於 frequency domain. 不過在深入之前, 一定要先了解 convolution 在 input 為 block-by-block 的情況下如何加速. 本文內容主要參考 Partitioned convolution algorithms for real-time auralization by Frank Wefers (書的介紹十分詳盡).

Convolution 分類如下: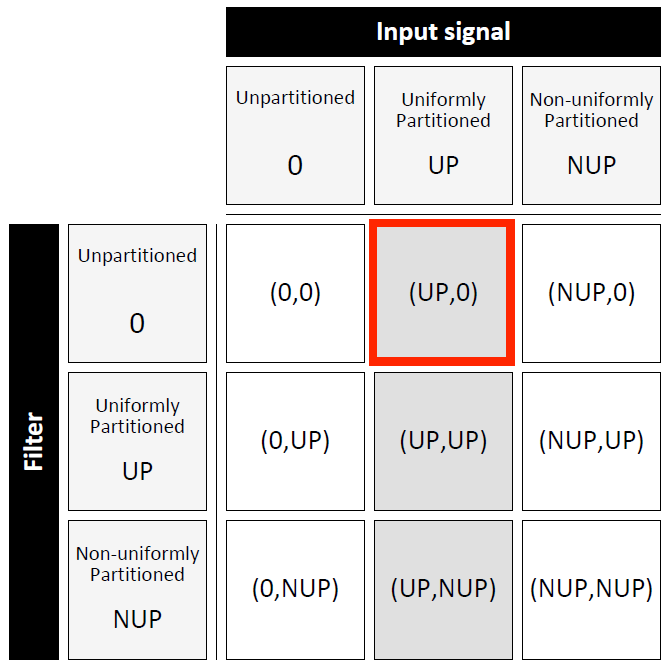

我們就針對最常使用的情形介紹: Input (UP) and Filter (0).

這是因為實際應用 input 是 infinite length, 所以需要 block-by-block 給定, 而 filter 通常都是 finite length, 可以選擇不 partition, 或 uniformly partitioned 以便得到更低的延遲效果.

針對 block-based input 的 convolution, 我們有兩種架構:

OverLap-and-Add (OLA)
OverLap-and-Save (OLS)

Linear Convolution

Filter $h$ 長度為 $N$ 個, 對 input $x$ 做 convolution 為:

$$
\begin{align}
y[i]=\sum_{n=0}^{N-1} h[n] \cdot x[i-n]
\end{align}
$$

考慮 $h={h[0],h[1],h[2]}$, $x={x[0], x[1], x[2], x[3]}$ 的 case
根據 (1), 得知 $y[2]=h[0]x[2]+h[1]x[1]+h[2]x[0]$. 如下圖: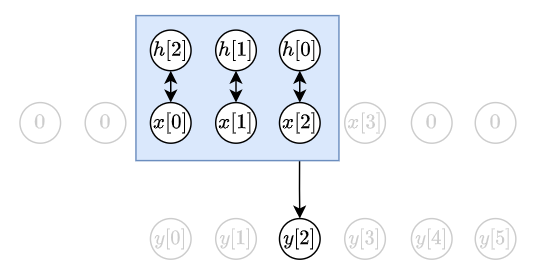
在舉個例子, $y[3]=h[0]x[3]+h[1]x[2]+h[2]x[1]$. 如下圖:
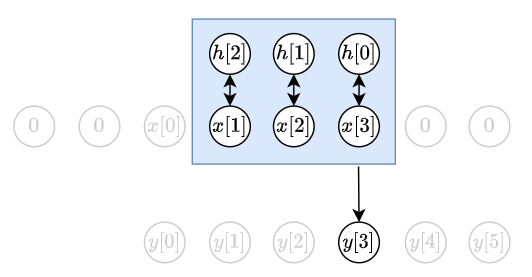所以整個 linear convolution $y=x\star h$ 為:
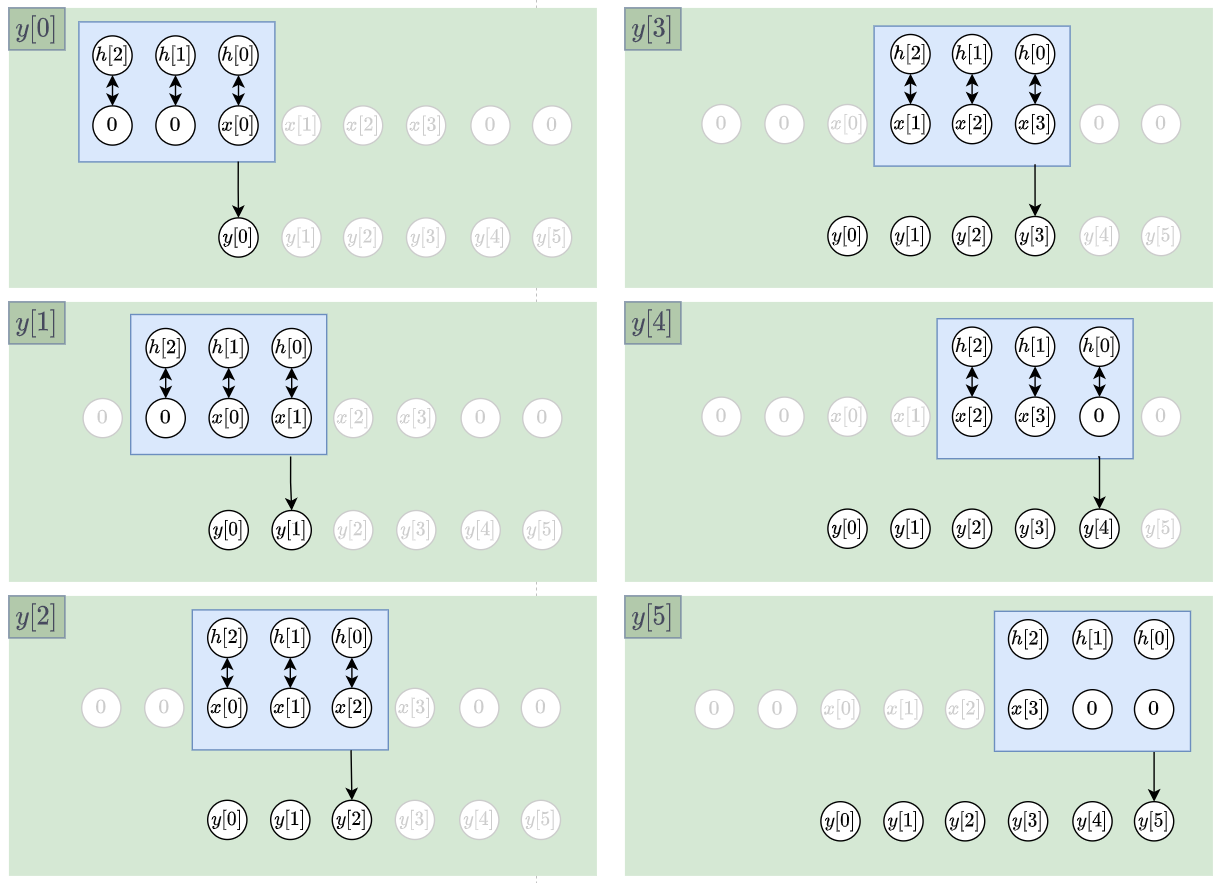因此當 $|h|=N$, $|x|=M$, 則 output $|y|=M+N-1$

OLA

OLA 相對來說很好理解的. 每一個新來的 data block $x_i$ (長度為 $B$), 都與 filter $h$ (長度為 $N$) 做 linear convolution, 產生的 output $y_i$ (長度為 $B+N−1$) 開頭的 $N−1$ 個結果與前一個output block 重疊的部分疊加 (“add”), 所以稱 overlap-and-ADD. 示意圖如下:
當 input 是一個 block 一個 block 近來的時候, (每個 block 長度為 $4$), ola 圖示為: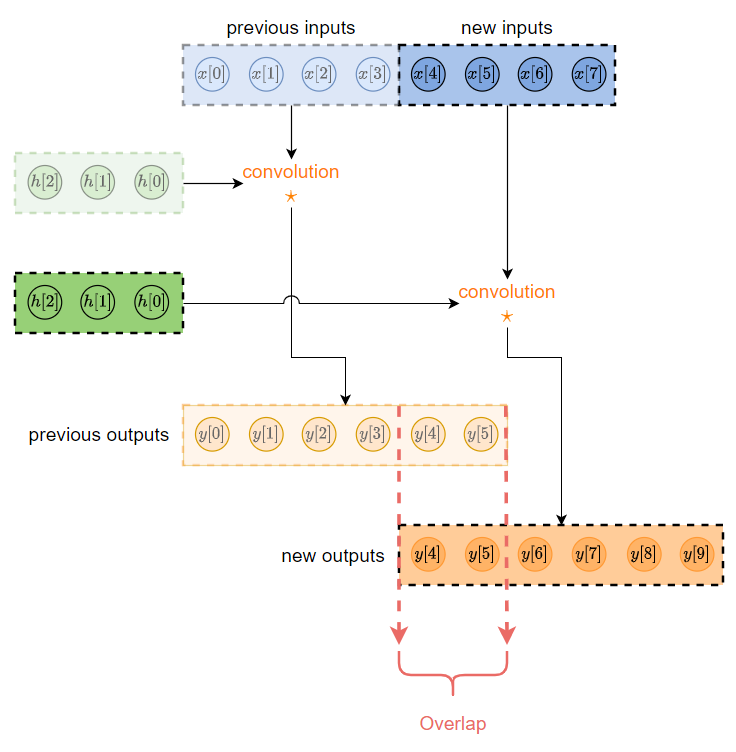

OLS

OLS 則從 output 角度來看. 根據現在的 output 來決定需要用到那些 inputs 做 linear convolution.
舉例來說根據 convolution 定義, 式 (1), 如果我們需要計算 $y[6]$ 則我們需要用到 ${x[6], x[5], x[4]}$, i.e. $y[6]=h[0]x[6]+h[1]x[5]+h[2]x[4]$
因此根據此筆新 data ${x[4], x[5], x[6], x[7]}$, 我們可以得到相對應的 outputs ${y[4], y[5], y[6], y[7]}$. 如下圖所示:

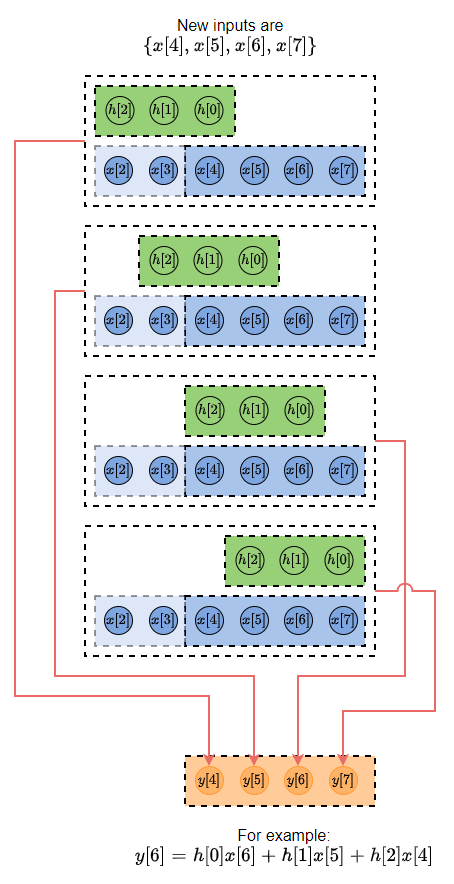
data block 長度為 $B$, filter $h$ 長度為 $N$

如果我們把新的 block data ${x[4], x[5], x[6], x[7]}$ 結合 $N-1$ 個過去 data 使得 data $x={x[2], x[3], x[4], x[5], x[6], x[7]}$ 整體長度為 $B+N-1$. 根據上圖與 $h$ 做 linear convolution, 則有效 output 點如上圖所示只會有 $B(=4)$ 個是我們要的! 因此我們只需要 “save” 需要的這 $B$ 個 output, 其他都丟較即可. 所以稱 overlap-and-SAVE.

如何有效率的做 linear convolution?

不管是 OLA 或 OLS 都需要對兩個固定長度 (通常使用 padding $0$ 成等長) 的 signal 做 linear convolution. 怎麼有效率的做 linear convolution 就變得十分重要.
我們都知道頻域的相乘相當於時域的 circular convolution. 因此如果能用 ciruclar convolution 來做出 linear convolution 的話, 我們就能轉到頻域上再相乘就可以了.
Circular convolution 的定義如下[1], 其實概念也很容易:

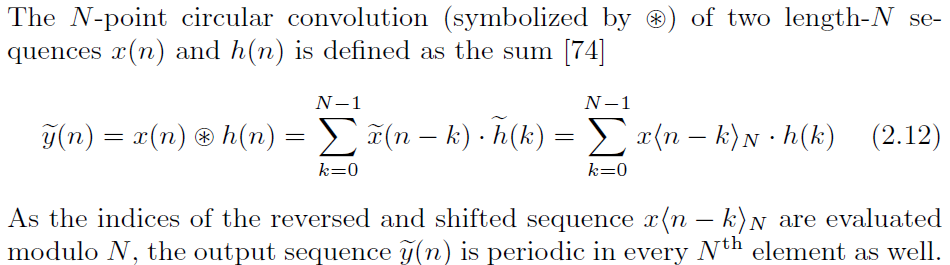
我們只需要適當地 padding zeros, 就可以使得 padding 後的 signals 做 circular convolution 會等於原來的 singals 做 linear convolution. 如下圖[1]

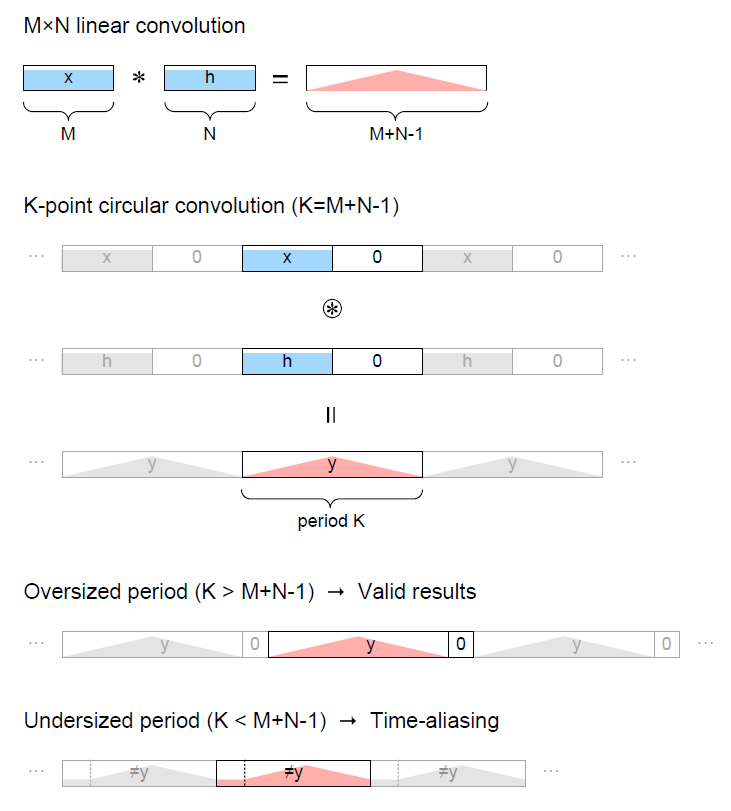
因此使用 FFT-domain 的 circular convolution 來實現 fast linear convolution 流程如下

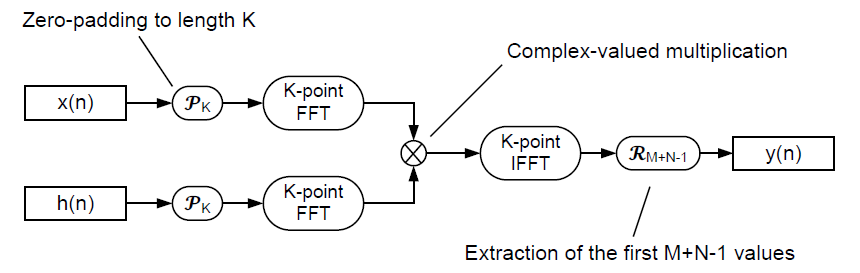
Fast Conv with OLA

在 OLA 架構中使用 FFT-domain 的 circular convolution 如下:

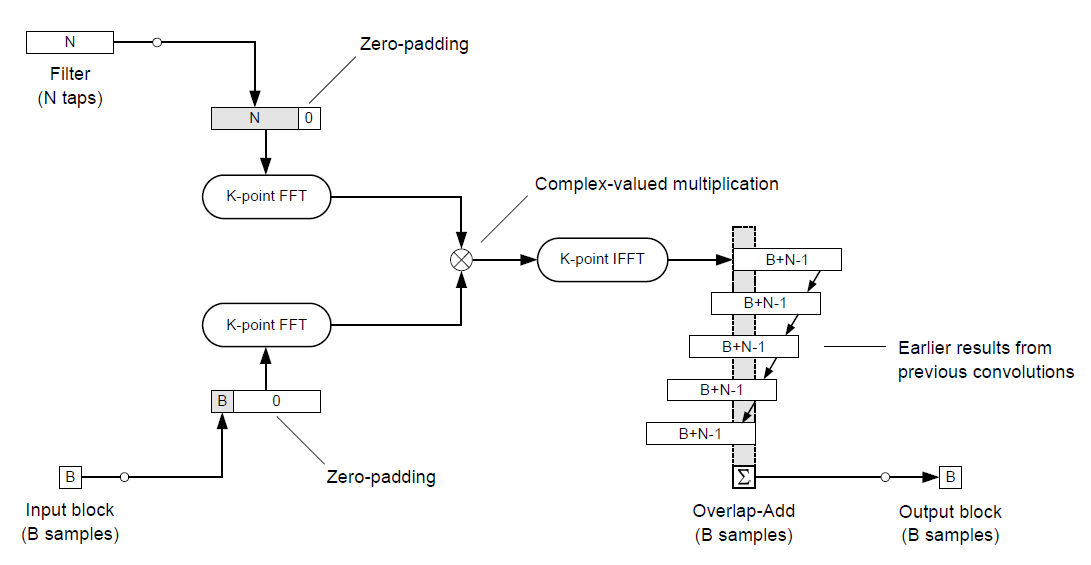
Padding zeros 不管在前還是在後都可以, 只要滿足 $K=\geq M+B-1$ 避免 aliasing 即可.

Fast Conv with OLS

在 OLS 架構中使用 FFT-domain 的 circular convolution 如下:

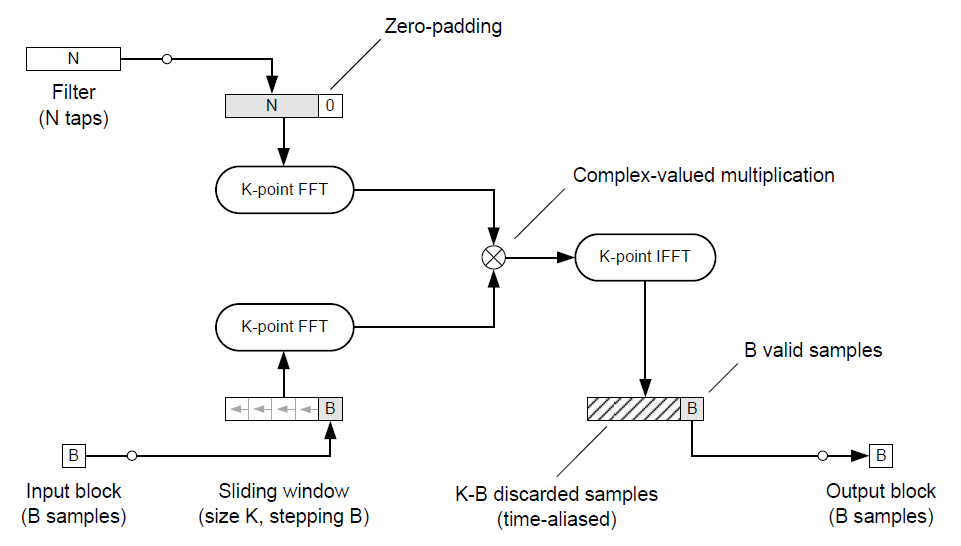
Input signal 不是 padding zeros, 而是在左邊 padding 之前的 input 訊號 (參考本篇上面的 OLS 段落), 用這樣的 padding 方式來看 circular convolution 的話, 每一次我們就 “save” output 的最後 $B$ 個結果即可.

在實作上通常會將 $B=N$, 並且設定 $K=2B=2N$, 這樣我們每一次只需要保留前一次的 input block, 並且 padding 給新來的 input block.

Frequncy Domain Adaptive Filter

Frequency Domain Adaptive Filter (FDAF) 請參考 [2], 整理的非常好, 所以這裡就不多描述, 完全可以照著實作出來! 我們會發現其實它採用的是我們上面說過的 Fast Convolution with OLS 架構, 只是 filter 必須 adaptive 更新.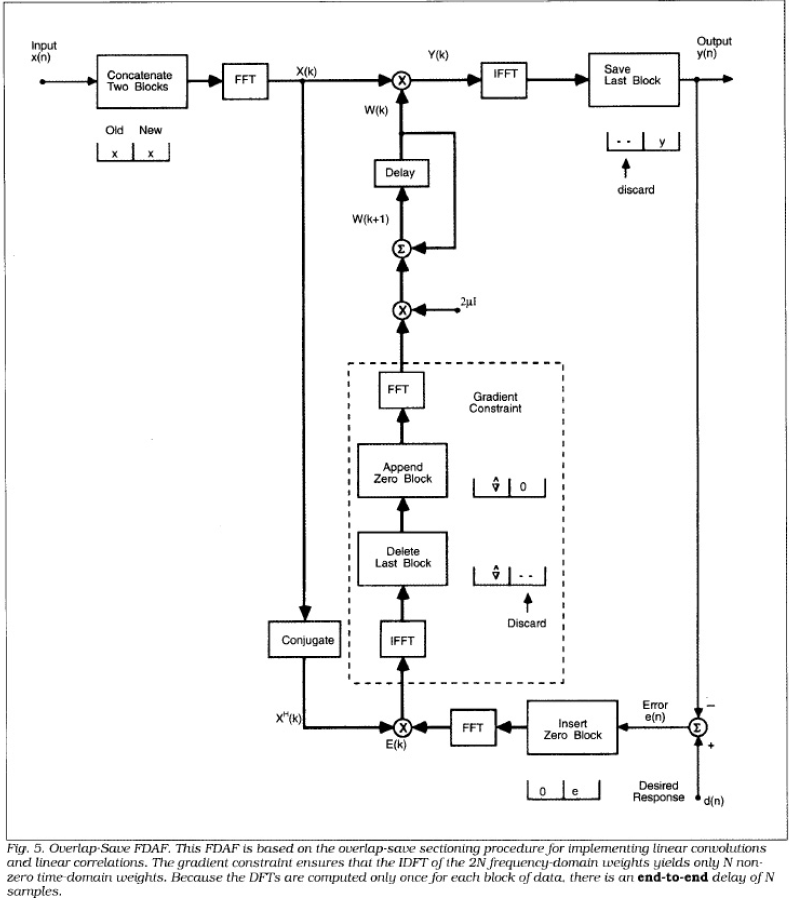

以下是 python implementation

# In the frequency domain methods, notations are defined as:
# x: reference signal, [-1, 1]
# d: desired signal, [-1, 1]
# step_size: step size
# alpha: the alpha filter for tracking the energy for each bin
# w: the retruned filter
# e: the error signal, of size (itr_num,)
# ========== FDAF (Frequency Domain Adaptive Filters)
def FDAF(x,d,step_size,N=512,alpha=0.9):
  iter_num = len(d)//N-1
  assert(iter_num>0)
  # Init
  W = np.zeros(2*N,dtype=complex)
  pow_lambda = np.ones(2*N)*np.finfo(np.float32).eps
  rtn_e = np.zeros((iter_num-1)*N)
  # Main Iteration
  for itridx in range(1,iter_num):
    x_2blocks = x[(itridx-1)*N:(itridx+1)*N]  # (2N)
    d_block = d[itridx*N:(itridx+1)*N]  # (N)
    X = fft(x_2blocks) # (2N)
    Y = np.einsum('i,i->i',X,W)
    y = ifft(Y) # (2N)
    y = y[N:] # (N), discard first half block
    # print (y)
    # e = np.real(d_block - y) # (N)
    e = d_block - y # (N)
    # print(len(rtn_e))
    rtn_e[(itridx-1)*N:itridx*N] = np.real(e)
    e = np.concatenate([np.zeros([N]),e]) # (2N)
    E = fft(e) # (2N)
    
    pow_lambda = alpha*pow_lambda + (1-alpha)*(np.abs(X)**2)
    
    # scale error signal, just like NLMS
    E = E/pow_lambda
    # Set the upper bound of E, to prevent divergence
    m_errThreshold = 0.2
    Enorm = np.abs(E) # (2N)
    # print(E)
    for eidx in range(2*N):
      if Enorm[eidx]>m_errThreshold:
        E[eidx] = m_errThreshold*E[eidx]/(Enorm[eidx]+1e-10)
    
    # Constraint Part
    gradient = np.einsum('i,i->i',X.conj(),E) # (2N)
    gradient = ifft(gradient)
    gradient[N:] = 0
    gradient = fft(gradient) # (2N)
    
    # Update Part
    W = W + step_size*gradient
  return rtn_e

Summary

我們介紹了針對 input 是 block-by-block 給定時, 計算 linear convolution 的兩種架構: OLA, OLS.

而如何加速 linear convolution 我們則介紹了使用 circular convolution 來等價地完成 linear convolution. Circular convolution 可以利用頻域相乘來加快速度 (得益於 FFT 的效率).

除了對 input 切 block 之外, 我們也還可以對 filter $h$ 切 block, 這樣的好處是計算量可以在更低, 且 latency 也會降低. 這部分請參考書的 Ch5, 附上一張書本裡的架構圖:

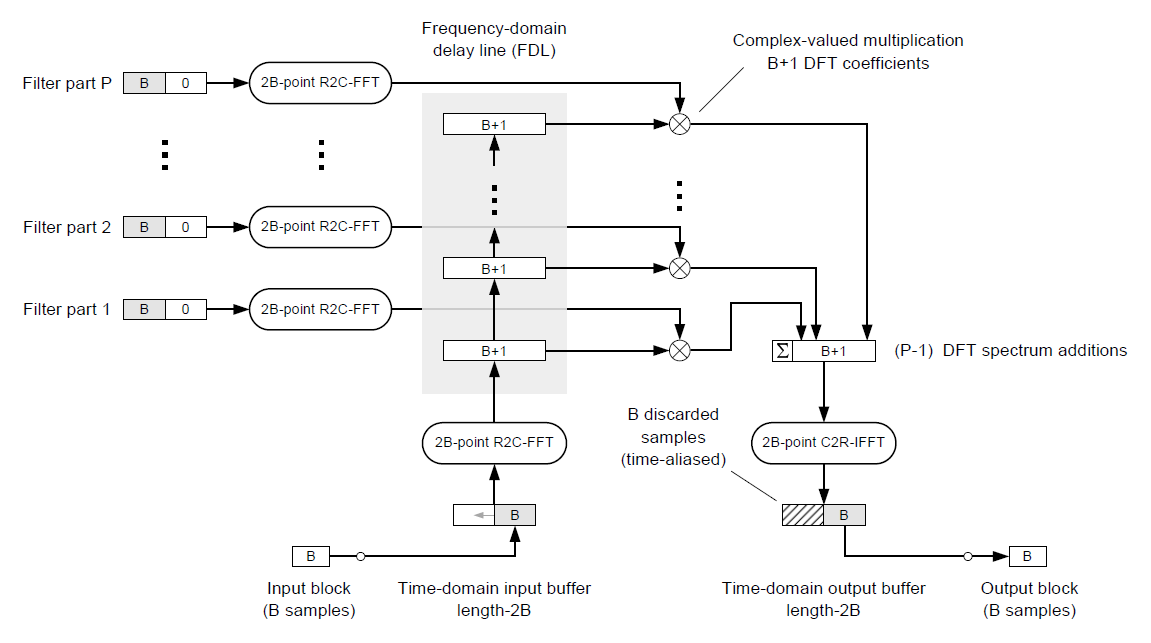
這種方式其實很重要, 原因是 webrtc 中的 AEC 採用的是 Partitioned Block Frequency Domain Adaptive Filter (PBFDAF) [3], 就是 filter 也是 uniformly partitioned.

最後我們利用 OLA 和 fast convolution, 列出來 frequency domain AF 的架構圖. 同時如果想要進一步降低 latency 則需使用 PBFDAF[3] (filter 也 partition).