SphereFace: Deep Hypersphere Embedding for Face Recognition 使得訓練出來的 embeddings 可以很好的使用 cosine similarity 做 verification/identification. 可以先網路上搜尋一下其他人的筆記和討論, 當然直接看論文最好.
一般來說我們對訓練集的每個人用 classification 的方式訓練出 embeddings, 然後在測試的時候可以對比兩個人的 embeddings 來判斷是否為同一個人. 使用 verification 當例子, 實用上測試的人不會出現在訓練集中, 此情形稱為 openset 設定.
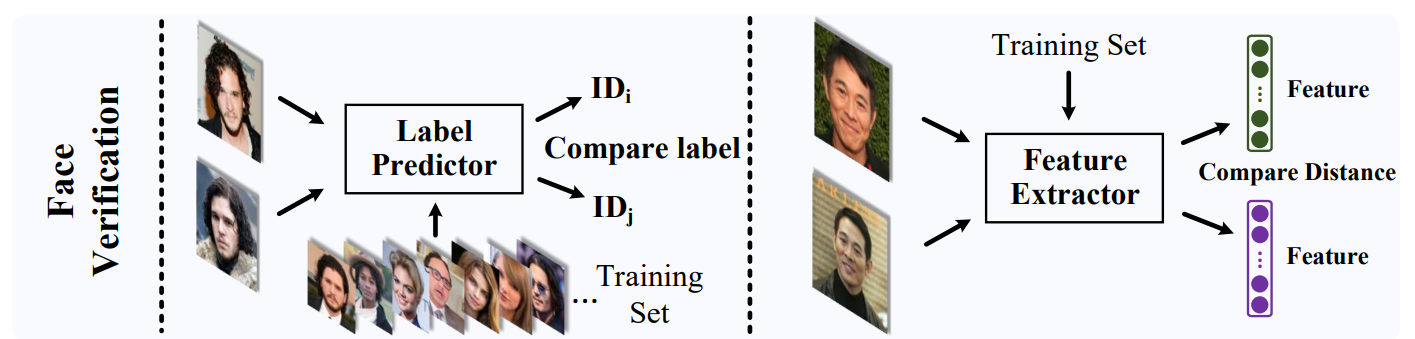
注意到 embedding 是使用 classification 方式訓練出來, 也就是說, 如果訓練集有 1000 個人, 最後一層的 softmax 就有 1000 個 nodes. 然後 embedding 一般取 softmax 前一層 (前兩層也可).
測試時常見的做法就是計算兩個 embeddings 的 cosine similarity, 直觀上相同的人他們的 embedding 會接近, 因此夾角小 (cosine 大), 而不同的人夾角大 (cosine 小).
但問題來了, 當初訓練 embedding 時並沒有針對 classification 用夾角來分類, 也就不能保證 softmax loss 對於使用 cosine similarity 是最有效的.
Modified softmax loss (M-softmax loss) 和 Angular softmax loss (A-softmax loss) 就能針對這種情形 (測試時使用 cosine similarity) 計算 loss. A-softmax loss 比 M-softmax loss 條件更嚴苛, 除了希望針對 angular 做分類外, 還希望同一類的夾角能聚再一起, 不同類的夾角能盡量分開.
下面就說明一下 softmax loss, M-softmax loss and A-softmax loss, 然後以 tensorflow 的實作來說明
Softmax Loss
其實沒什麼好說明的, 公式如下
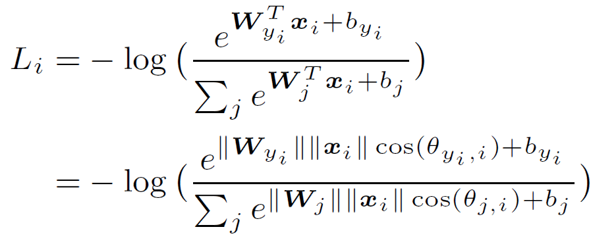
Decision boundary 以兩類來看如下:
$$\begin{align} (W_1 - W_2)x+b_1 - b_2=0 \end{align}$$M-Softmax Loss
如果我們將 $W_j$ 的 norm 限制為 1, 且去掉 biases, $b_j=0$, 則原來的 softmax loss 變成如下:
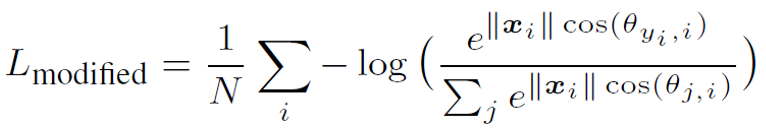
Decision boundary 以兩類來看如下:
$$\begin{align} \parallel x \parallel (\cos \theta_1 - \cos \theta_2)=0 \Rightarrow \cos \theta_1 = \cos \theta_2 \end{align}$$我們可以發現 decision boundary 完全由夾角來決定了!
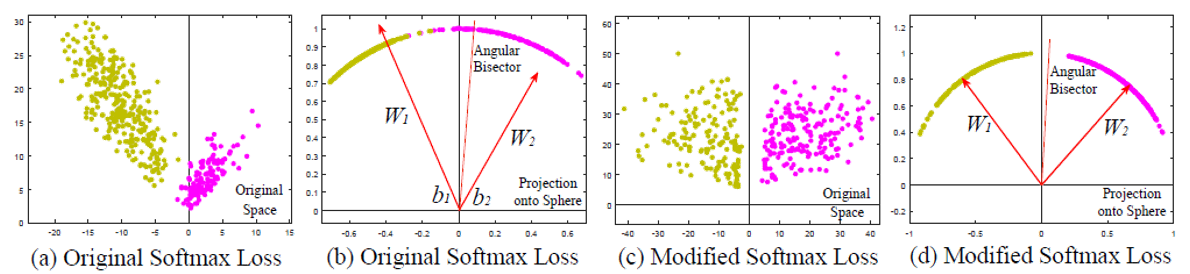
論文使用 toy example 來說明 M-softmax loss 造成的現象:
A-Softmax Loss
以兩類來說明, M-softmax loss 將 $x$ 分類成 class 1 的條件為 $\cos \theta_1 > \cos \theta_2$, 也就是 $\theta_1 < \theta_2$. A-softmax loss 則讓這個條件更嚴格, 它希望 $m$ 倍的 $\theta_1$ 都還小於 $\theta_2$, 因此條件為 $\cos m\theta_1 > \cos \theta_2$. 論文中以幾何的方式說明很清楚:
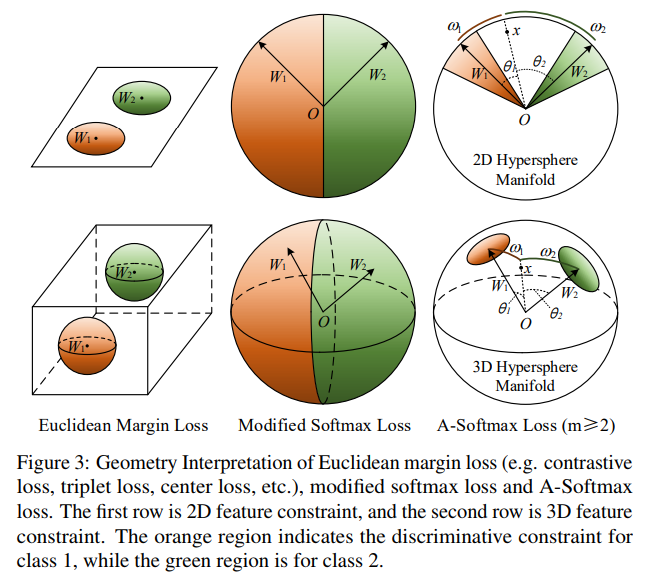
因此 A-softmax loss 如下:
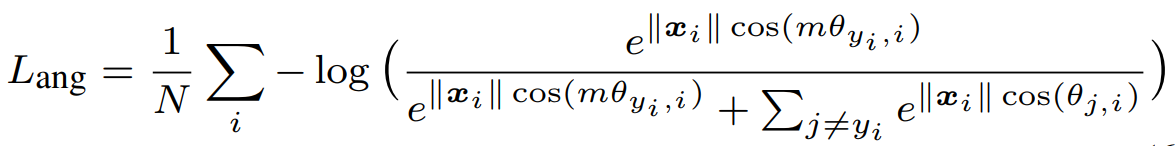
論文使用 toy example 來說明 A-softmax loss 造成的現象:

可以看到相比於 M-softmax loss, A-softmax loss 會使得 margin 增大
這種 within class 靠近, between class 拉遠就如同 LDA 的概念. A-softmax 也能造成這種效果且是在 angular 的 measure 下. 而常見的情形都是針對 euclidean distance, 例如使用 triplet loss (推薦這篇 blog 說明具體且 tensorflow 實現非常厲害).
原則上我們希望與 class $i$ 的夾角 $\theta_i$ 愈小, 所算出來的 logits 也就是 $\cos\theta_i$ 要愈大, 所以放大 $m$ 倍的夾角所算出來的 logits, $\cos m\theta_i$ 必須要變小.
但由於 $\cos$ 是 periodic function, 一旦 $m\theta_i$ 超過 $2\pi$ 就反而可能使得 logits 變大, 這就適得其反了. 精確來說 $\cos m\theta_i < \cos\theta_i$ 只會在 $\theta_i$ 屬於 $[0,\pi/m]$ 區間範圍內成立. 因此我們必須對 A-softmax loss 作如下改動:
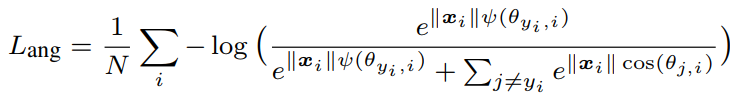 其中
其中
我們將 $\psi$ 畫出來:
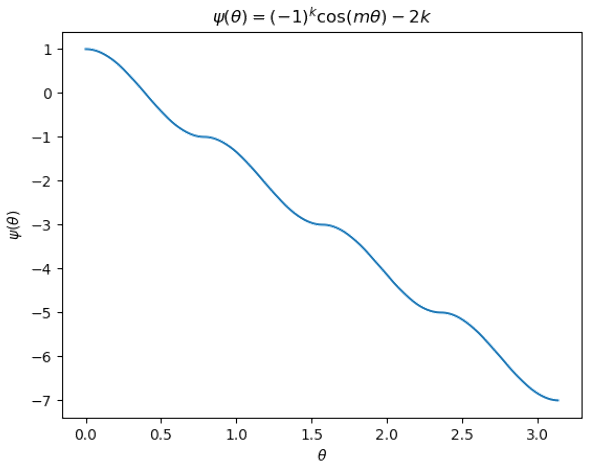
兩個觀察:
- 首先 $\psi$ 的確會隨著角度變大而變小, 這符合我們要的 logits 的行為.
- 再來要計算出正確的 $\psi(\theta)$ 必須要先知道 $k$, 也就是需要知道 $\theta$ 落在哪個區間才行.
第二點可能比較棘手, 我們思考一下怎麼在 tensorflow 的 graph 中實現 ….
hmm…. 好像有點麻煩
Tensorflow Implementation A-softmax Loss
其實網路上就很多 tensorflow 的實現了, 不看還好, 一看才發現 A-softmax loss 的 $\psi$ 實現步驟如下:
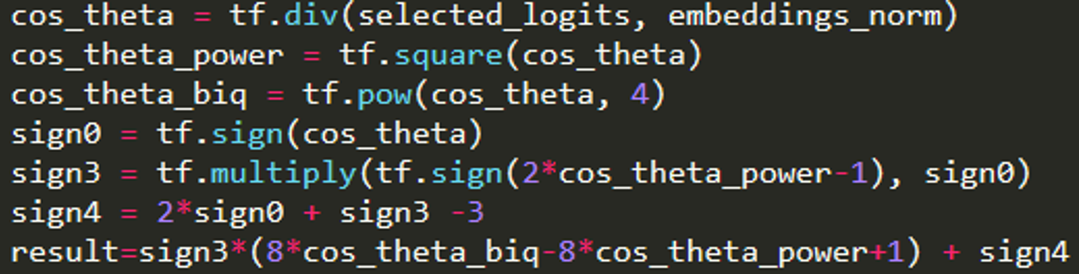
這什麼操作?! 怎麼跟原來理解的 (3) and (4) 長相差這麼多! 網路上幾乎大家都直接拿來用, 也沒什麼說明. 不過我們仔細分析一下, 還是能發現端倪.
首先注意到這樣的實現是基於 $m=4$ 做的. (論文的實驗最後在這個設定有不錯的效果) 因此將 $m=4$ 套入 (3)(4) 得:
接著我們作如下分析:
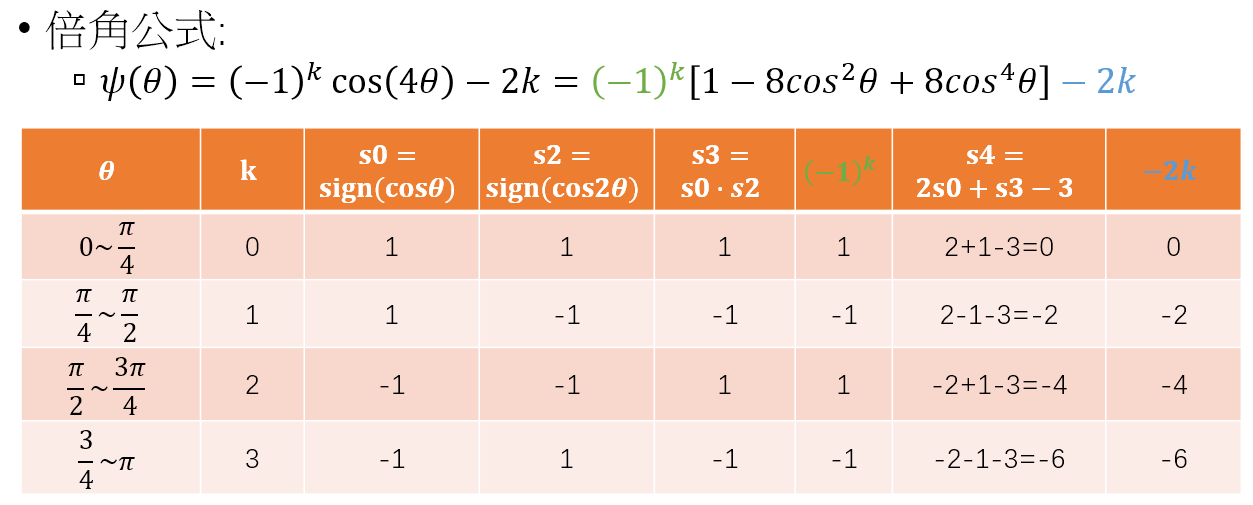
發現 $s3=(-1)^k$ 和 $s4=-2k$, 因此
$$\begin{align} \psi(\theta)=\color{green}{(-1)^k} \cos(4\theta)\color{blue}{-2k} = \color{green}{s3}[1-8\cos^2\theta +8\cos^4\theta]\color{blue}{+s4} \end{align}$$而 $\cos\theta$ 則因為 weights $W$ 的 norm 限制為 1, 所以只需要 $Wx$ 再除以 $x$ 的 norm 即可. 到這裡最麻煩的實作問題分析完畢, 依樣畫葫蘆也可以做出 $m=2$, $m=3$.
Summary
Take home messages:
- M-softmax loss 算出來的 embeddings 在 test 階段可以直接用 cosine measure
- A-softmax loss 更進一步使得各類別之間的角度拉更開, 達到 large margin 效果
- A-softmax loss 實作上不好訓練, 可以使用論文中提到的訓練方法, 一開始偏向原來的 softmax loss, 然後漸漸偏向 A-softmax loss
- M-softmax loss 簡單實用, 經過 weight norm = 1 的條件, 論文中說明能去掉 prior 分布