整理下 entropy 的一些東西, 不然久沒看老是忘記.
- Entropy of a r.v. $X$: $H(X)$
- Conditional Entropy of $Y$ given $X$: $H(Y|X)$
- Cross(Relative) Entropy of two pdf, $p$ and $q$: $D(p\Vert q)$
- Mutual Information of two r.v.s: $I(X;Y)$
文章會明確定義每一項, 然後在推導它們之間關係的同時會解釋其物理意義.
最後其實就可以整理成類似集合關係的圖 (wiki)
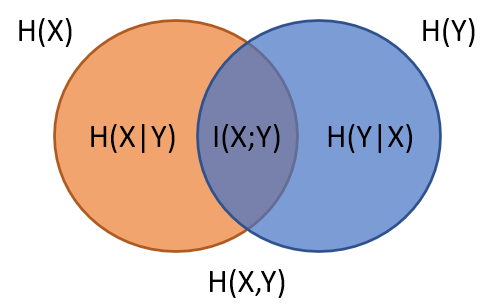
Entropy
$$\begin{align} H(X) = \sum_{x\in X}{p(x)\log{\frac{1}{p(x)}}} \end{align}$$一個 r.v. $X$ 假設配給他的 pdf 為 $p$, 則可以算出相對應的 entropy $H(X)$, 所以我們其實可以看成是 $H(p)$.
可以知道當 $p$ 是 uniform distribution 時 entropy 達到最大 (後面再證明). 同時該定義可以很容易看出 $H(X)\geq 0$.
直觀解釋:
- 因為 uniform distribution 時最大 (最無法確定哪一個 outcome 最有可能), 另一個極端為 $X$ 為 constant (r.v. 只有一個 outcome) 所以我們可以理解為 entropy 為量測一個 r.v. $X$ 的不確定性
- 如果要對每一個 outcome 決定要用多少 bit 來代表, 我們希望平均花的 bits 數能最小, 直觀上機率愈大的 outcome 用愈小的 bits 來表達. 因此 outcome $x_i$ 我們用 $\log{\frac{1}{p(x_i)}}$ 這麼多 bits 表示, 則 entropy 代表了 encode 所有 outcome 所需要的平均 bits 數, 則這個數是最小的. (這可以從下面的 cross entropy 得到證明)
- 我們可以用 entropy 來表示該 r.v. 所包含的資訊量. 因為比 entropy 更多的資訊量都是 reduandant 的 (由上一點可看出)
為了方便我們會交叉使用 資訊量 或是 encode 的最小平均 bits 數 來表示 entropy 的物理意義.
Cross(Relative) Entropy
為量測兩個 pdfs, $p(x)$ and $q(x)$ 之間的 “divergence”, 也稱為 KL divergence. 注意 divergence 不需滿足三角不等式也不需滿足對稱性, 因此不是一個 “metric”. 但也足夠當成是某種”距離”來看待 (不是指數學上的 norm)
$$\begin{align} D(p\Vert q) = \sum_x{p(x)\log{\frac{p(x)}{q(x)}}} \end{align}$$由 Jensen’s inequality 可以推得 $D(p\Vert q) \geq 0$, 另外 $D(p\Vert q)=0$ iff $p=q$
$$\begin{align} D(p\Vert q) = - \sum_x{p(x)\log{\frac{q(x)}{p(x)}}} \\ \text{by Jensen's inequality: } \geq \log\sum_x{p(x)\frac{q(x)}{p(x)}} = 0 \end{align}$$
重寫一下 (2):
$$\begin{align}
0\leq D(p\Vert q) = \sum_x{p(x)\log{\frac{1}{q(x)}}} - H(p)
\end{align}$$
這說明了對於 outcome $x_i$ (true distribution 為 $p(x)$) 我們用 $\log{\frac{1}{\color{red}{q}(x_i)}}$ 這麼多 bits 表示是浪費的. 所以證明了上面 Entropy 第二種解釋.
直觀解釋:
- $D(p\Vert q)$ 表示使用錯誤的 distribution $q$ 來 encode 要多花的平均 bits 數量
Conditional Entropy
$$\begin{align} H(Y|X) = \sum_{x\in X}{p(x)H(Y|x=X)} \\ =\sum_x{p(x)\sum_y{p(y|x)\log{\frac{1}{p(y|x)}}}} \end{align}$$$H(Y|x=X)$ 解釋為 given $x$ encode $Y$ 的最小平均 bits 數 (就是 entropy 只是又重複說了一次), 但是每一個 $x$ 有自己的機率, 因此對 $x$ 再取一次平均.
case 1:
如果 $Y$ 完全可以由 $X$ 決定, 因此一旦給定 $x$, $Y$ 就是一個 constant, 所以 $H(Y|x=X)=0$. 再對 $X$ 算期望值仍然是 0.case 2:
$$\begin{align} (7)=\sum_x{p(x)\sum_y{p(y)\log{\frac{1}{p(y)}}}}=\sum_x{p(x)H(Y)}=H(Y) \end{align}$$
如果 $X$ and $Y$ independent.得到結論 $H(Y|X)=H(Y)$
Case 1 and 2 說明了 $X$ and $Y$ 在完全依賴和完全無關時 $H(Y|X)$ 分別為 $0$ and $H(Y)$. 直覺上我們可以認為 $0\leq H(Y|X) \leq H(Y)$, 因為剛好是兩個極端情形. 但直覺是不夠的, 我們證明一下.
使用定義, 我們可以很容易推導出
$$\begin{align} \color{orange}{I(X;Y)\equiv}H(Y)-H(Y|X)=\sum_{x,y}{p(x,y)\log{\frac{p(x,y)}{p(x)p(y)}}} \\ =D(p(x,y)\Vert p(x)p(y)) \geq 0 \end{align}$$我們這裡先偷跑出了 mutual information $I(X;Y)$ 的定義, 下面會再詳細講.
直觀解釋:
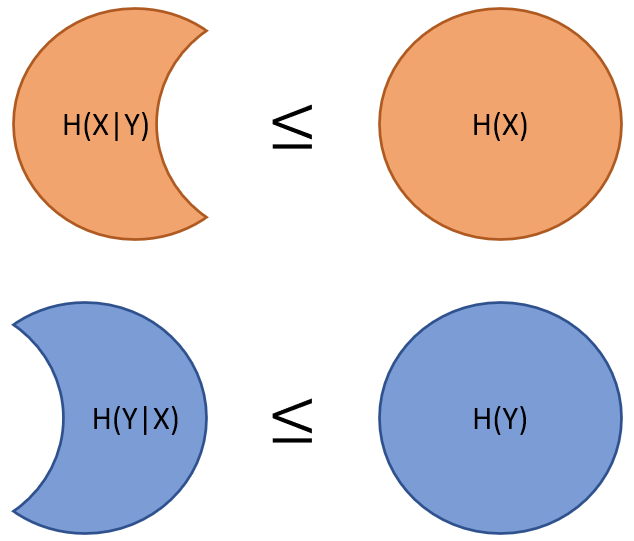
$H(Y|X)$ 表示給了 $X$ 的資訊後, $Y$ 剩下的資訊量. 其中 $0\leq H(Y|X) \leq H(Y)$
Chain Rule for Entropy
我們在把 (7) 做個運算:
$$\begin{align} H(Y|X)=(7)=-\sum_x{p(x)\sum_y{p(y|x)\log{p(y|x)}}} \\ =-\sum_{x,y}{p(x,y)\log{\frac{p(x,y)}{p(x)}}} \\ =-\sum_{x,y}{p(x,y)\log{p(x,y)}}+\sum_{x,y}{p(x,y)\log{p(x)}} \\ =H(X,Y) - H(X) \end{align}$$直觀解釋:
給定 $X$ 後 $Y$ 剩下的資訊量 ($H(Y|X)$) 就等於 $X,Y$ 整體的資訊量扣掉單獨 $X$ 部分的資訊量
Mutual Information
(9) 已經先給出了定義, 我們這裡重複一次:
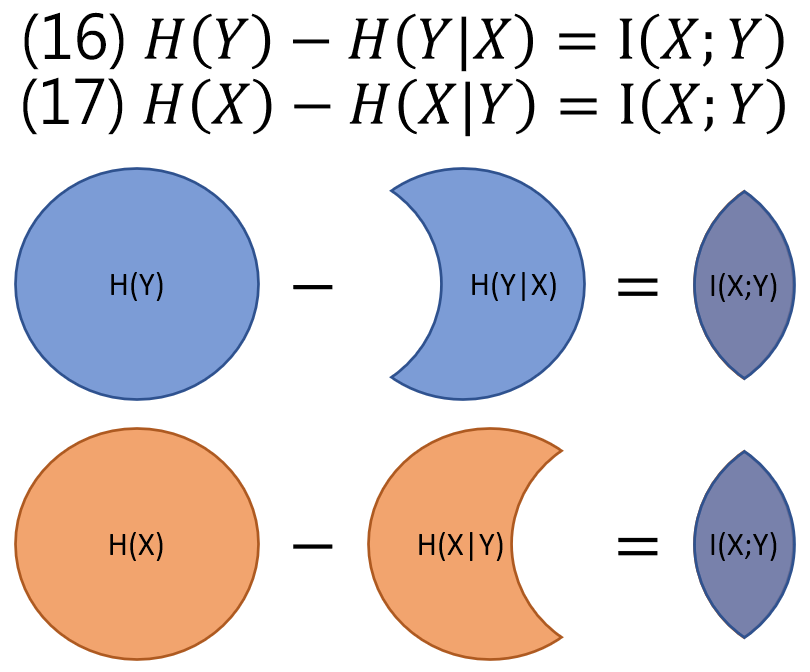
$$\begin{align} I(X;Y)\equiv\sum_{x,y}{p(x,y)\log{\frac{p(x,y)}{p(x)p(y)}}} =D(p(x,y)\Vert p(x)p(y))\\ \text{(用 entropy 定義得到) }=H(Y)-H(Y|X) \\ \text{(用 entropy 定義得到) }=H(X)-H(X|Y) \end{align}$$在用 Chain Rule for Entropy: $H(Y)=H(X,Y)-H(X|Y)$ 代進 (16) 得到
$$\begin{align} I(X;Y)=H(X,Y)-H(Y|X)-H(X|Y) \end{align}$$我知道這麼多式子一定眼花了….好在完全可以用集合的 Venn diagram 表示!
所有式子的直觀表達

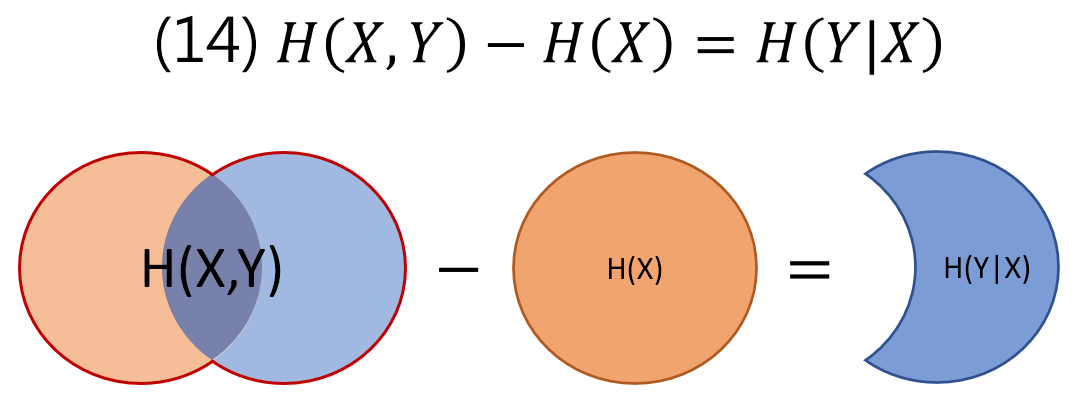
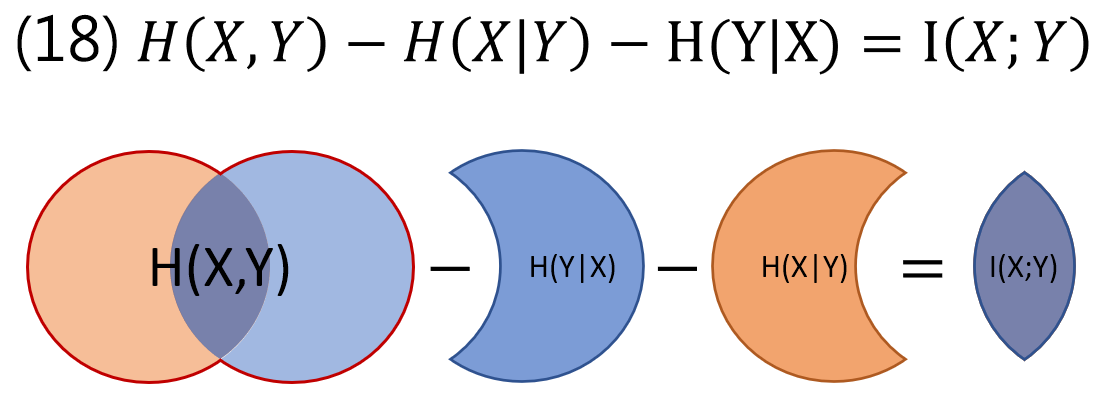
Reference
- wiki mutual information
- Dr. Yao Xie, ECE587, Information Theory, Duke University 本篇內容只是 lecture 1 ~ 4 的範圍