Noise Contrastive Estimation (NCE) 筆記

之前聽人介紹 wav2vec [3] 或是看其他人的文章大部分都只有介紹作法, 直到有一天自己去看論文才發現看不懂 CPC [2] (wav2vec 使用 CPC 方法). 因此才決定好好讀一下並記錄.

先將這些方法關係梳理一下, NCE –> CPC (infoNCE) –> wav2vec. 此篇筆記主要紀錄 NCE (Noise Contrastive Estimation)

在做 ML 時常常需要估計手上 training data 的 distribution $p_d(x)$. 而我們通常會使用參數 $\theta$, 使得參數的模型跟 $p_d(x)$ 一樣. 在現在 DNN 統治的年代可能會說, 不然就用一個 NN 來訓練吧, 如下圖:

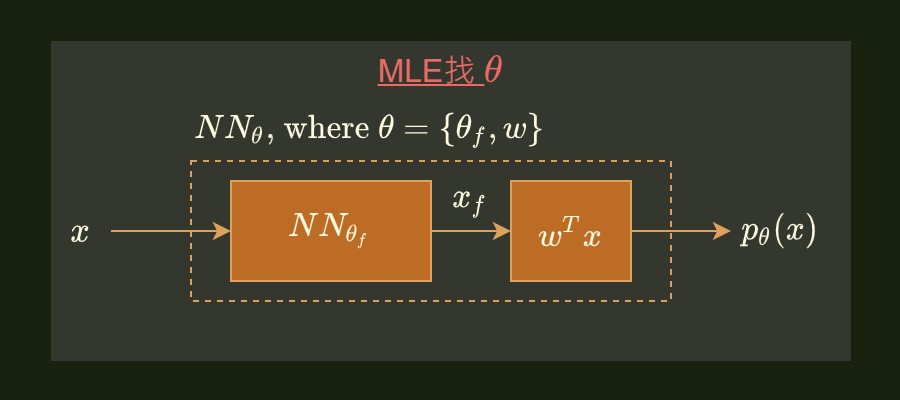
給 input $x$, 丟給 NN 希望直接吐出 $p_\theta(x)$. 上圖的架構是 $x$ 先丟給參數為 $\theta_f$ 的 NN, 該 NN 最後一層的 outputs 再丟給參數為 $w$ 的 linear layer 最後吐出一個 scalar 值, 該值就是我們要的機率.
而訓練的話就使用 MLE (Maximum Likelihood Estimation) 來求參數 $\theta$.

恩, 問題似乎很單純但真正實作起來卻困難重重. 一個問題是 NN outputs 若要保持 p.d.f. 則必須過 softmax, 確保 sum 起來是 1 (也就是要算 $Z_\theta$).

$$\begin{align} p_\theta(x)=\frac{u_\theta(x)}{Z_\theta}=\frac{e^{G(x;\theta)}}{Z_\theta} \\ \text{where } Z_\theta = \sum_x u_\theta(x) \end{align}$$

式 (1) 為 energy-based model, 在做 NN classification 時, NN 的 output 就是 $G(x;θ)$, 也就是常看到的 logit, 經過 softmax 就等同於式 (1) 在做的事

而做這件事情在 $x$ 是 discrete space 但數量很多, 例如 NLP 中 LM vocabulary 很大時, 計算資源會消耗過大.
或是 $x$ 是 continuous space 但是算 $Z_\theta$ 的積分沒有公式解的情形會做不下去. (不然就要用 sampling 方法, 如 MCMC)

NCE 巧妙的將此 MLE 問題轉化成 binary classification 問題, 從而得到我們要的 MLE 解.

不過在此之前, 我們先來看看 MLE 的 gradient 長什麼樣.

MLE 求解

寫出 likelihood:

$$\begin{align} \text{likilhood}=\prod_{x\sim p_d} p_\theta(x) \end{align}$$

Loss 就是 negative log-likelihood

$$\begin{align} -\mathcal{L}_{mle}=\mathbb{E}_{x\sim p_d}\log p_{\theta}(x)= \mathbb{E}_{x\sim p_d}\log \frac{u_\theta(x)}{Z_\theta}\\ \end{align}$$

計算其 gradient:

$$\begin{align} -\nabla_{\theta}\mathcal{L}_{mle}= \mathbb{E}_{x\sim p_d} \left[ \nabla_{\theta}\log{u_\theta(x)} - \color{orange}{\nabla_{\theta}\log{Z_\theta}} \right] \\ \color{orange}{\nabla_{\theta}\log{Z_\theta}} = \frac{1}{Z_\theta}\nabla_{\theta}Z_\theta = \frac{1}{Z_\theta} \sum_x \nabla_{\theta} e^{G(x;\theta)} \\ =\frac{1}{Z_\theta} \sum_x e^{G(x;\theta)} \nabla_{\theta}G(x;\theta) = \sum_x \left[ \frac{1}{Z_\theta}e^{G(x;\theta)} \right] \nabla_{\theta}G(x;\theta) \\ =\sum_x p_{\theta}(x) \nabla_{\theta} \log u_{\theta}(x) = \mathbb{E}_{x \sim p_{\theta}} \nabla_{\theta} \log u_{\theta}(x) \\ \therefore \text{ } -\nabla_{\theta}\mathcal{L}_{mle} = \mathbb{E}_{x\sim p_d} \left[ \nabla_{\theta} \log u_{\theta}(x) - \color{orange}{\mathbb{E}_{x \sim p_{\theta}} \nabla_{\theta} \log u_{\theta}(x)} \right] \\ = \mathbb{E}_{x\sim p_d} \nabla_{\theta} \log u_{\theta}(x) - \mathbb{E}_{x \sim p_{\theta}} \nabla_{\theta} \log u_{\theta}(x)\\ = \sum_x \left[ p_d(x) - p_{\theta}(x) \right] \nabla_{\theta} \log u_{\theta}(x) \\ \end{align}$$

從 (11) 式可以看到, 估計的 pdf 與 training data 的 pdf 差越大 gradient 愈大, 當兩者相同時 gradient 為 0 不 update.

Sigmoid or Logistic Function

在說明 NCE 之前先談一下 sigmoid function. 假設現在我們做二分類問題, 兩個類別 $C=1$ or $C=0$. 令 $p$ 是某個 input $x$ 屬於 class 1 的機率 (所以 $1-p$ 就是屬於 class 0 的機率)
定義 log-odd 為 (其實也稱為 logit):

$$\begin{align} \text{log-odd} = \log \frac{p}{1-p} \end{align}$$

我們知道 sigmoid function $\sigma(x)=\frac{1}{1+e^{-x}}$ 將實數 input mapping 到 0 ~ 1 區間的函式. 若我們將 log-odd 代入我們很容易得到:

$$\begin{align} \sigma(\text{log-odd})=...=p \end{align}$$

發現 sigmoid 回傳給我們的是 $x$ 屬於 class 1 的機率值, i.e. $\sigma(\text{log-odd})=p(C=1|x)$. 所以在二分類問題上, 我們就是訓練一個 NN 能 predict logit 值.

NCE 的 Network 架構

首先 NCE 引入了一個 Noise distribution $q(x)$. 論文提到該 $q$ 只要滿足當 $p_d(x)$ nonzero 則 $q(x)$ 也必須 nonzero 就可以.

二分類問題為, 假設要取一個正例 (class 1), 就從 training data pdf $p_d(x)$ 取得. 而若要取一個反例 (class 0) 則從 noise pdf $q(x)$ 取得.
我們可以取 $N_p$ 個正例以及 $N_n$ 個反例, 代表 prior 為:

$$\begin{align} p(C=1)=\frac{N_p}{N_p+N_n} \\ p(C=0)=1-p(C=1) \\ \end{align}$$

因此就可以得到一個 batch 共 $N_p+N_n$ 個 samples, 丟入下圖的 NN structure 做二分類問題:

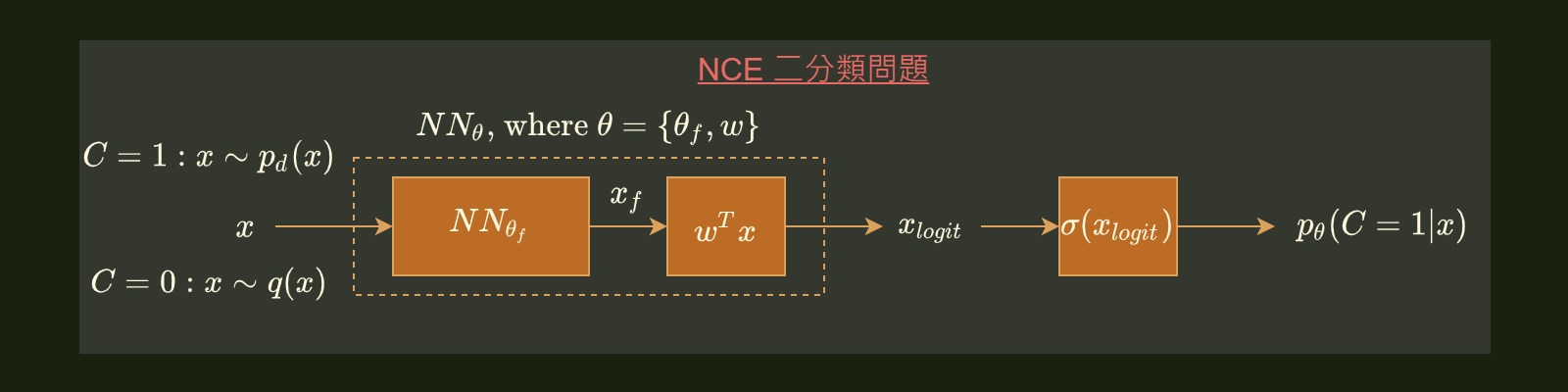
Network 前半段還是跟原來的 MLE 架構一樣, 只是我們期望 $NN_{\theta}$ 吐出來的是 logit, 由上面一個 section 我們知道經過 sigmoid 得到的會是 $x$ 屬於 class 1 的機率. 因此很容易就用 xent loss 優化.

神奇的來了, NCE 告訴我們, optimize 這個二分類問題得到的 $\theta$ 等於 MLE 要找的 $\theta$!

$$\begin{align} \theta_{nce} = \theta_{mle} \end{align}$$

且 NN 計算的 logit 直接就變成 MLE 要算的 $p_{\theta}(x)$.

同時藉由換成二分類問題, 也避開了很難計算的 $Z_{\theta}$ 問題.
為了不影響閱讀流暢度, 推導過程請參照 Appendix

所以我們可以透過引入一個 Noise pdf 來達到估計 training data 的 generative model 了. 這也是為什麼叫做 Noise Contrastive Estimation.

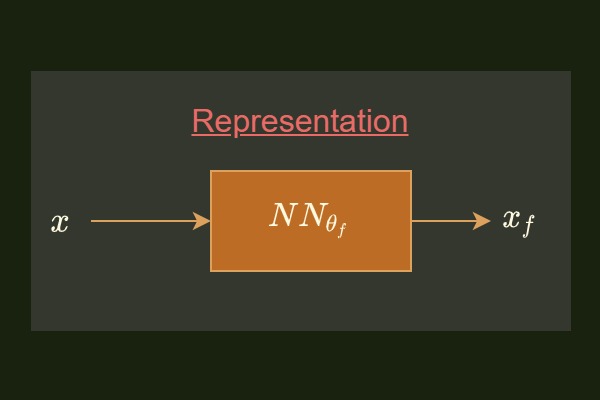
Representation

由於透過 NCE 訓練我們可以得到 $\theta$, 此時只需要用 $\theta_f$ 的 NN 來當作 feature extractor 就可以了.

總結

最後流程可以總結成下面這張圖:

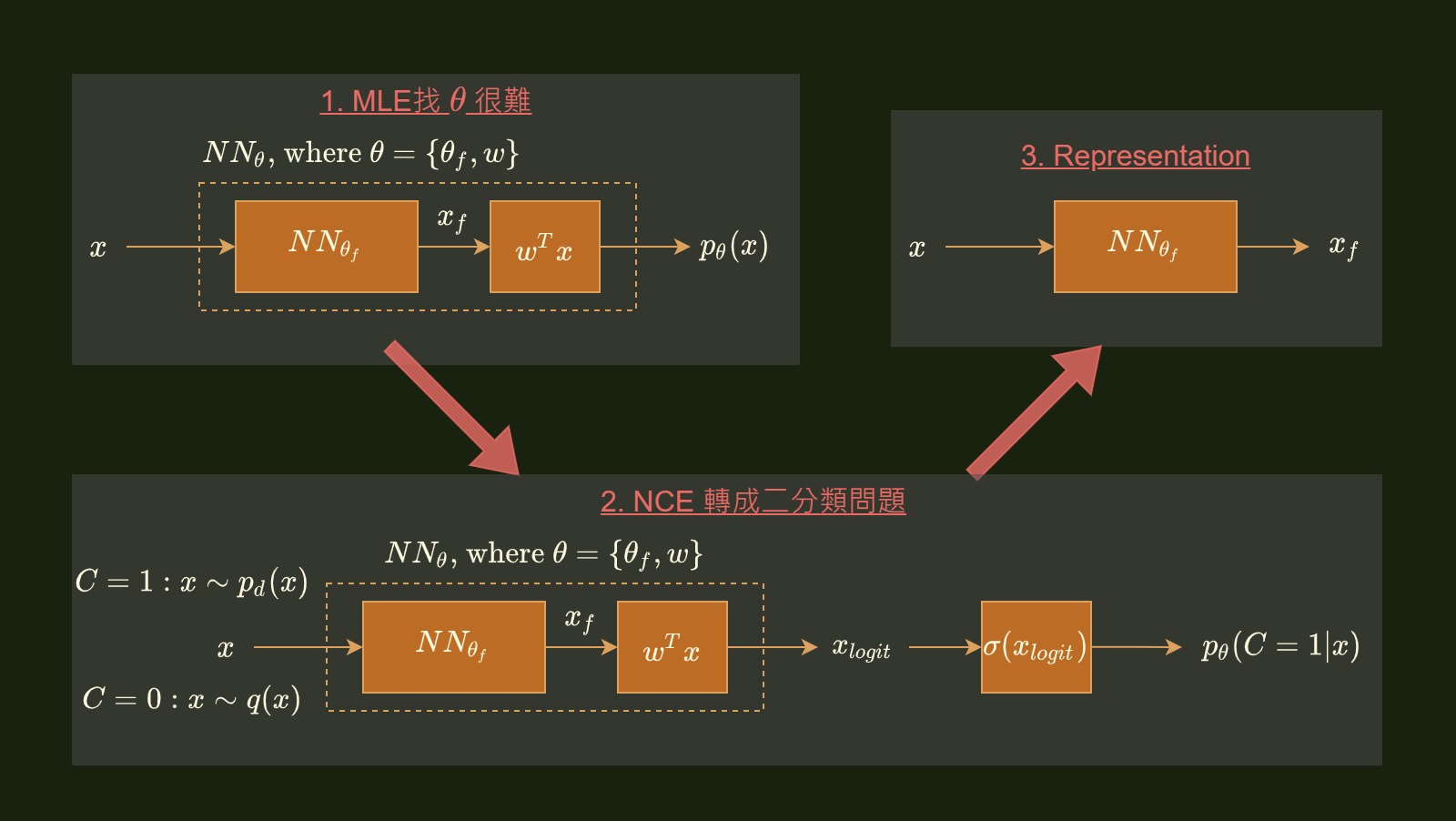
最後聊一下 CPC (Contrastive Predictive Coding) [2]. 我覺得跟 NCE 就兩點不同:

我們畫的 NCE 圖裡的 $w$, 改成論文裡的 $c_t$, 所以變成 network 是一個 conditioned 的 network
不是一個二分類問題, 改成 N 選 1 的分類問題 (batch size $N$, 指出哪一個是正例), 因此用 categorical cross-entorpy 當 loss

所以文章稱這樣的 loss 為 infoNCE loss

同時 CPC [2] 論文中很棒的一點是將這樣的訓練方式也跟 Mutual Information (MI) 連接起來.
證明了最小化 infoNCE loss 其實就是在最大化 representation 與正例的 MI (的 lower bound).

這些背後數學撐起了整個利用 CPC 在 SSL (Self-Supervised Learning) 的基礎. 簡單講就是不需要昂貴的 label 全部都 unsupervised 就能學到很好的 representation.
而近期 facebook 更利用 SSL 學到的好 representation 結合 GAN 在 ASR 達到了 19 年的 STOA WER. 論文: Unsupervised Speech Recognition or see [9]

SSL 好東西, 不試試看嗎?

Appendix

Prior pdf:
$$\begin{align} p(C=1)=\frac{N_p}{N_p+N_n} \\ p(C=0)=1-p(C=1) \\ \end{align}$$

Generative pdf:
$$\begin{align} p(x|C=1)=p_{\theta}(x) \\ p(x|C=0)=q(x) \end{align}$$

因此 Posterior pdf:
$$\begin{align} p(C=1|x)=\frac{p(C=1)p(x|C=1)}{p(C=1)p(x|C=1)+p(C=0)p(x|C=0)}=\frac{p_{\theta}(x)}{p_{\theta}(x)+N_r q(x)} \\ p(C=0|x)=\frac{p(C=0)p(x|C=0)}{p(C=1)p(x|C=1)+p(C=0)p(x|C=0)}=\frac{N_r q(x)}{p_{\theta}(x)+N_r q(x)} \\ \end{align}$$
其中 $N_r=\frac{N_n}{N_p}$

因此 likelihood 為:
$$\begin{align} \text{likilhood}=\prod_{t=1}^{N_p} p(C_t=1|x_t) \cdot \prod_{t=1}^{N_n} p(C_t=0|x_t) \end{align}$$

Loss 為 negative log-likelihood:
$$\begin{align} - \mathcal{L}_{nce} = \sum_{t=1}^{N_p} \log p(C_t=1|x_t) + \sum_{t=1}^{N_n} \log p(C_t=0|x_t) \\ = N_p \left[ \frac{1}{N_p} \sum_{t=1}^{N_p} \log p(C_t=1|x_t) \right] + N_n \left[ \frac{1}{N_n} \sum_{t=0}^{N_n} \log p(C_t=0|x_t) \right] \\ \propto \left[ \frac{1}{N_p} \sum_{t=1}^{N_p} \log p(C_t=1|x_t) \right] + N_r \left[ \frac{1}{N_n} \sum_{t=0}^{N_n} \log p(C_t=0|x_t) \right] \end{align}$$

當固定 $N_r$ 但是讓 $N_p\rightarrow\infty$ and $N_n\rightarrow\infty$. 意味著我們固定正負樣本比例, 但取無窮大的 batch. 重寫上式成:
$$\begin{align} - \mathcal{L}_{nce} = \mathbb{E}_{x\sim p_d} \log p(C=1|x) + N_r \mathbb{E}_{x\sim q} \log p(C=0|x) \\ \therefore \text{} -\nabla_{\theta}\mathcal{L}_{nce} = \nabla_{\theta}\left[ \mathbb{E}_{x\sim p_d} \log \frac{p_{\theta}(x)}{p_{\theta}(x)+N_rq(x)} + N_r\mathbb{E}_{x\sim q} \log \frac{N_rq(x)}{p_{\theta}(x)+N_rq(x)} \right] \\ = \mathbb{E}_{x\sim p_d} \color{orange}{\nabla_{\theta} \log \frac{p_{\theta}(x)}{p_{\theta}(x)+N_rq(x)}} + N_r \mathbb{E}_{x\sim q} \color{green}{\nabla_{\theta} \log \frac{N_rq(x)}{p_{\theta}(x)+N_rq(x)} } \end{align}$$

計算橘色和綠色兩項, 之後再代回來:

$$\begin{align} \color{orange}{\nabla_{\theta} \log \frac{p_{\theta}(x)}{p_{\theta}(x)+N_rq(x)}} = \nabla_{\theta}\log\frac{1}{1+N_r\frac{q(x)}{p_{\theta}(x)}} = -\nabla_{\theta}\log \left( 1+\frac{N_rq(x)}{p_{\theta}(x)} \right) \\ = -\frac{1}{1+\frac{N_rq(x)}{p_{\theta}(x)}}\nabla_{\theta}\frac{N_rq(x)}{p_{\theta}(x)} = -\frac{N_rq(x)}{1+\frac{N_rq(x)}{p_{\theta}(x)}}\nabla_{\theta}\frac{1}{p_{\theta}(x)} \\ = -\frac{N_rq(x)}{1+\frac{N_rq(x)}{p_{\theta}(x)}} \frac{-1}{p_{\theta}^2(x)} \nabla_{\theta} p_{\theta}(x) \\ = \frac{N_rq(x)}{p_{\theta}(x)+N_rq(x)} \left[ \frac{1}{p_{\theta}(x)} \nabla_{\theta} p_{\theta}(x) \right] \\ = \frac{N_rq(x)}{p_{\theta}(x)+N_rq(x)} \nabla_{\theta} \log p_{\theta}(x) \end{align}$$ $$\begin{align} \color{green}{\nabla_{\theta} \log \frac{N_rq(x)}{p_{\theta}(x)+N_rq(x)}} = -\nabla_{\theta} \log\left( 1+\frac{p_{\theta}(x)}{N_rq(x)} \right) = -\frac{1}{1+\frac{p_{\theta}(x)}{N_rq(x)}} \nabla_{\theta} \frac{p_{\theta}(x)}{N_rq(x)} \\ = -\frac{1}{N_rq(x)+p_{\theta}(x)} \nabla_{\theta} p_{\theta}(x) \\ = -\frac{p_{\theta}(x)}{N_rq(x)+p_{\theta}(x)} \left[ \frac{1}{p_{\theta}(x)} \nabla_{\theta} p_{\theta}(x) \right] \\ = -\frac{p_{\theta}(x)}{N_rq(x)+p_{\theta}(x)} \nabla_{\theta} \log p_{\theta}(x) \end{align}$$

將 (34), (38) 代回去 (29) 得到:

$$\begin{align} - \nabla_{\theta}\mathcal{L}_{nce} = \mathbb{E}_{x\sim p_d} {\color{orange}{\frac{N_rq(x)}{p_{\theta}(x)+N_rq(x)} \nabla_{\theta} \log p_{\theta}(x)}} - N_r \mathbb{E}_{x\sim q} {\color{green}{\frac{p_{\theta}(x)}{N_rq(x)+p_{\theta}(x)} \nabla_{\theta} \log p_{\theta}(x)}} \\ = \sum_x \left[ p_d(x) \frac{N_rq(x)}{p_{\theta}(x)+N_rq(x)} \nabla_{\theta} \log p_{\theta}(x) \right] - \sum_x \left[ q(x) \frac{N_r p_{\theta}(x)}{N_rq(x)+p_{\theta}(x)} \nabla_{\theta} \log p_{\theta}(x)\right] \\ = \sum_x \frac{(p_d(x)-p_{\theta}(x))N_rq(x)}{p_{\theta}(x)+N_rq(x)} \nabla_{\theta}\log p_{\theta}(x) \\ = \sum_x \frac{(p_d(x)-p_{\theta}(x))q(x)}{\frac{p_{\theta}(x)}{N_r}+q(x)} \nabla_{\theta}\log p_{\theta}(x) \\ \end{align}$$

當 $N_r\rightarrow\infty$ 意味著我們讓負樣本遠多於正樣本, 上式變成:
$$\begin{align} \lim_{N_r\rightarrow\infty} - \nabla_{\theta}\mathcal{L}_{nce} = \sum_x \frac{(p_d(x)-p_{\theta}(x))q(x)}{0+q(x)} \nabla_{\theta}\log p_{\theta}(x) \\ = \sum_x (p_d(x)-p_{\theta}(x)) \nabla_{\theta}\log p_{\theta}(x) \\ = \sum_x \left[ p_d(x) - p_{\theta}(x) \right] \left( \nabla_{\theta}\log u_{\theta}(x) -\nabla_{\theta}\log Z_{\theta} \right) \end{align}$$

此時我們發現這 gradient 也與 Noise pdf $q(x)$ 無關了!

最後我們將 MLE and NCE 的 gradient 拉出來對比一下:
$$\begin{align} -\nabla_{\theta}\mathcal{L}_{mle} = \sum_x \left[ p_d(x) - p_{\theta}(x) \right] \nabla_{\theta} \log u_{\theta}(x) \\ -\nabla_{\theta}\mathcal{L}_{nce} = \sum_x \left[ p_d(x) - p_{\theta}(x) \right] \left( \nabla_{\theta}\log u_{\theta}(x) -\nabla_{\theta}\log Z_{\theta} \right) \end{align}$$

我們發現 MLE and NCE 只差在一個 normalization factor (or partition) $Z_{\theta}$.
最魔術的地方就在於 NCE 論文 [1] 證明最佳解本身的 logit 已經是 probability 型式, 因此也不需要 normalize factor.

論文裡說礙於篇幅沒給出證明, 主要是來自 Theorem 1 的結果:

所以我們不妨將 $Z_{\theta}=1$, 結果有:

$$\begin{align} \color{red} {\nabla_{\theta}\mathcal{L}_{mle} = \nabla_{\theta}\mathcal{L}_{nce}} \\ \color{red} {\Rightarrow \theta_{mle} = \theta_{nce}} \\ \end{align}$$

MLE 求解

Sigmoid or Logistic Function

NCE 的 Network 架構

Representation

總結

Appendix

Reference