Weight Normalization 的筆記

使用 SGD 做優化時, 如果 ill-conditioned of Hessian matrix, i.e. $\sigma_1/\sigma_n$ 最大最小的 eigenvalues 之比值, 會使得收斂效率不彰
(ref zig-zag).

可以想成 loss function 的曲面愈不像正圓則愈 ill-conditioned (愈扁平).

希望藉由 re-parameterization 來將 ill-conditioned 狀況降低.
一般來說 NN 的 layer 可以這麼寫:
$$y=\phi(w^Tx+b)$$ 把 weight vector $w$ 重新改寫如下:

$$w={g\over\|v\|}v\quad\quad(\star)$$ WN 就是將 $w$ 拆成用 unit vector $v/||v||$ 和 magnitude $g$ 兩個 variables 來表示

對大小 $g$ 的微分

因此 loss function $L$ 對 $g$ 微分為:
$$\begin{align} \frac{dL}{dg}=\nabla_wL^T\frac{\partial w}{\partial g}=\nabla_wL^T\frac{v}{\|v\|} \end{align}$$

這裡我們寫 gradient vector 都以 column vector 來寫
所以如果 loss function $L$ 是 scalar 的話, gradient 就是 transpose of Jacobian matrix (剛好是 1xn 的 row vector)

對方向向量 $v$ 的微分

Loss function $L$ 對 $v$ 微分為:

這裡要參考到 matrix cookbook equation (130)

$$\begin{align} \nabla_vL^T = \nabla_wL^T\left(g\frac{I}{\|v\|}-g\frac{vv^T}{\|v\|^3}\right)\quad \\ = \nabla_wL^T\frac{g}{\|v\|}\left( I-\frac{vv^T}{\|v\|^2} \right)\quad \end{align}$$ $$\therefore \quad \nabla_vL=\frac{g}{\|v\|}M_v\nabla_wL \quad\text{where}\ M_v:=I-\frac{vv^T}{\|v\|^2}$$

論文裡式 (3) 的 gradient 推導可藉由將 (1) 代進到 (2) 裡得到.

$\nabla_vL$ 的物理意義

注意到由於 $v$ 跟 $w$ 是同方向但大小不同而已. 所以
$$M_v=I-\frac{vv^T}{\|v\|^2}=I-\frac{ww^T}{\|w\|^2}=:M_w$$

$$\begin{align} \therefore \quad \nabla_vL=\frac{g}{\|v\|}M_w\nabla_wL \quad\text{where}\ M_w:=I- \color{orange}{\frac{ww^T}{\|w\|^2}} \end{align}$$ 觀察一下 $M_w$ 裡的第二項 ((4) 的橘色部分) 乘上一個 vector $x$ 代表的意義:
$$\frac{w}{\|w\|}\cdot\frac{w^T}{\|w\|}\cdot x$$ 其中 $w/\|w\|$ 表示 $w$ 方向的 unit vector, 而 $w^Tx/\|w\|$ 表示 $x$ 投影在 $w$ 方向上的長度.

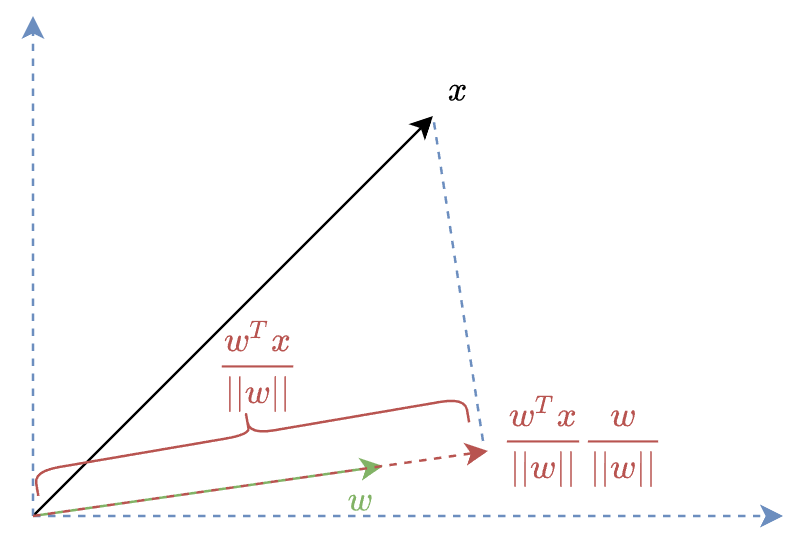
所以 $$M_w\nabla_wL=\nabla_wL-\frac{w}{\|w\|}\cdot\frac{w^T}{\|w\|}\cdot \nabla_wL$$ $M_w\nabla_wL$ 就是將 $\nabla_wL$ 扣掉在 $w$ 方向上的分量, 而 $\nabla_vL$ 只是再多乘一個 scalar,
也就是說 $\nabla_vL\perp w$, i.e. $w^T\nabla_vL=0$ (只要利用 (4) 計算就可知道)

SGD 會使得 $v$ 長度愈來愈大

用 SGD update $v$ 的時候公式為:
$$v'=v+\Delta v$$ 且 $\Delta v\propto\nabla_vL$ by steepest descent.
而因為 $\nabla_vL\perp w$ 所以 $\Delta v\perp w$. (要 update 的向量與目前的 weight 垂直)
由最開始的分解 $(\star)$ 我們知道 $v$ 與 weight $w$ 同方向. 所以自然 $\Delta v\perp v$.
這就導致了 update 後的 $v’$ 長度會比 $v$ 來得大 (三角不等式), 如下圖:

所以經過多次 SGD, $v$ 長度會愈來愈大.

與 Batch Normalization 的關聯

BN 在過一層 linear weight $v$ 後為:
$$\begin{align} v^Tf_{BN}(x)= v^T\left(g\cdot\frac{x-\mu}{\sigma}+b\right) \end{align}$$ 其中 $\mu,\sigma$ 都是從訓練時的 mini-batch 統計的, 而 $g,b$ 是 trainable 的參數
而 WN 對 weight $w$ 為 (不看 non-linear activation 那項):
$$f_{WN}(x;w)= w^Tx = {g\over\|v\|}v^Tx \\ = v^T\left(g\cdot\frac{x}{\|v\|}\right) = v^Tf_{BN}(x)$$ 對照 BN 可以知道設定 $\sigma=\|v\|,\mu=0,b=0$ 就變成 WN!
但 WN 的好處是不依賴 mini-batch 的設定, 這在如果 batch size 較小的情況會比較有利.

BN在Conv後會有Conv的Weight具有Scale Invariant特性

WN 對於 $v$ 會愈 update 愈大, 考慮 BN 是否也有這樣的狀況?
一般來說, 我們會這麼串: activation(BN(convolution(x)))
將 BN 放在 convolution 後 activation 之前, 這樣可以最後做完 quantizaiton 的時候, convolution 和 BN 的 weight 做融合.
令 $w$ 當作 convolution 的 weights, 如果 weights 做 $\alpha$ 倍的 scale: $w’=\alpha w$, 則對 BN 後的結果不會有影響, 這是因為 $\mu’=\alpha\mu$, and $\sigma’=\alpha\sigma$ 也跟著一起 scale
$$f_{BN}(\alpha w^Tx)=f_{BN}(w^Tx)$$ 明確寫出來一個 function $f$ 對 input $w$ 是 scale invariant:
$$f(\alpha w)=f(w),\quad \forall \alpha\in\mathbb{R}$$ 微積分我們學過 gradient vector 會跟 coutour 的 level curve 垂直
把 scale invariant function 的 “等高線” contour map 畫出來, 示意圖大概這樣:

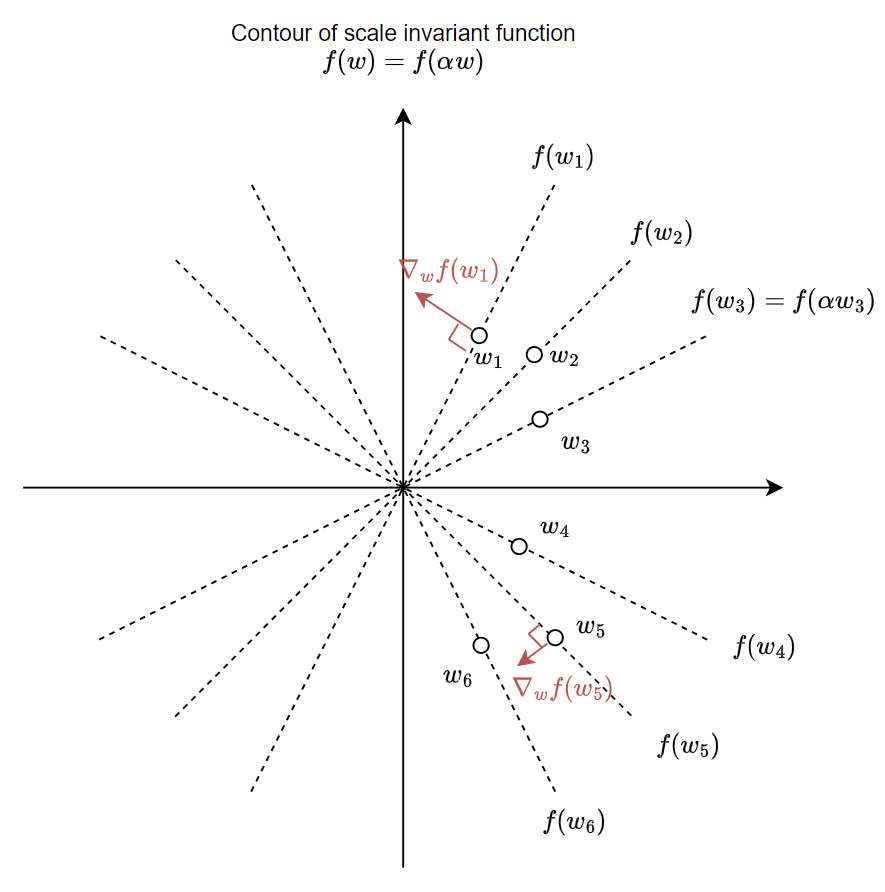
可以看到做 SGD update 的方向會跟 contour 垂直, 導致跟之前討論 WN $v$ 會愈來愈大的狀況一樣, Convolution 的 weight $w$ 也會隨著 SGD update 愈來愈大.
因此我們在使用 activation(BN(convolution(x))) 這樣的 layer 的時候可能會觀察到這樣的現象.
到這邊我們可能會擔心, 會不會訓練下去 $\|w\|_2$ 會發散?
通常來說不用擔心, 因為離零點愈遠則 gradient 愈小. 這是因為 loss surface 只跟角度有關, 離零點愈遠的 loss surface 會愈稀疏、平坦. 這樣一來雖然每次 update $\|w\|_2$ 都會變大, 但變大的幅度愈來愈小. 這篇 blog 文章 (by inFERENCe) 也有描述, 裡面的圖也解釋得很好.

💡 另外也可以 update 完 weight 後, 再把 convolution 的 weight 直接 normalized, 因為反正是 scale invariant function, 不影響輸出結果.

$v$ 和 $g$ 的初始化

可以參考 模型优化之Weight Normalization 的說明就好.
論文有題到 WN 對於 initialization 比較敏感

Pytorch 的 API

torch.nn.utils.weight_norm
注意 weight normalization 是這種形式:
$$y=\phi(w^Tx+b)$$ (markdown渲染怪怪的, 改用圖)

注意到 conv2d 一次的”內積” 是處理 in_channel * kernel_height * kernel_width, 所以一個 $w$ 的維度也是如此.
總共有 out_channel 這麼多個的 “內積”, 也就是有這麼多的 $w$.
另外, 把 stride or dilation 改動不會影響 weight_g and weight_v 的 size

Summary

WN 直接將參數拆成大小和方向向量分別 update. 希望藉由這樣拆解能減緩 ill-conditioned 狀況, 使模型收斂速度加快. 同時 WN 也不依賴 mini-batch, 這在 batch size 如果比較小的時候不會像 BN 效果變差, 或是比較適用於 RNN.
不過拆成這樣參數量也會增加, 但其實 BN 也需要額外的 memory 來存 $\mu,\sigma$, 這樣比就要看誰划算了.
另外探討了 activation(BN(convolution(x))) 有時會觀察到 Convolution 的 weight $w$ 也會隨著 SGD update 愈來愈大.
這個現象跟本文 WN 裡面討論到方向向量 $v$ 的大小也會愈 update 愈大道理是很像的.

不過目前遇到的實務上, 比較少使用 WN, 大部分還是用 BN, LN (Layer Normalization).
有效性我自己還要再多觀察

最後透過看這篇論文, 仔細推導裡面的數學和理解其物理意義, 這對我來說還是很有幫助的.