AWQ 筆記

發表於 | 分類於 | [object Object]

如同 SmoothQuant 論文裡的圖, 在 memory size 已經跟不上算力和模型大小情況下, memory bandwidth 已經變成 bottleneck.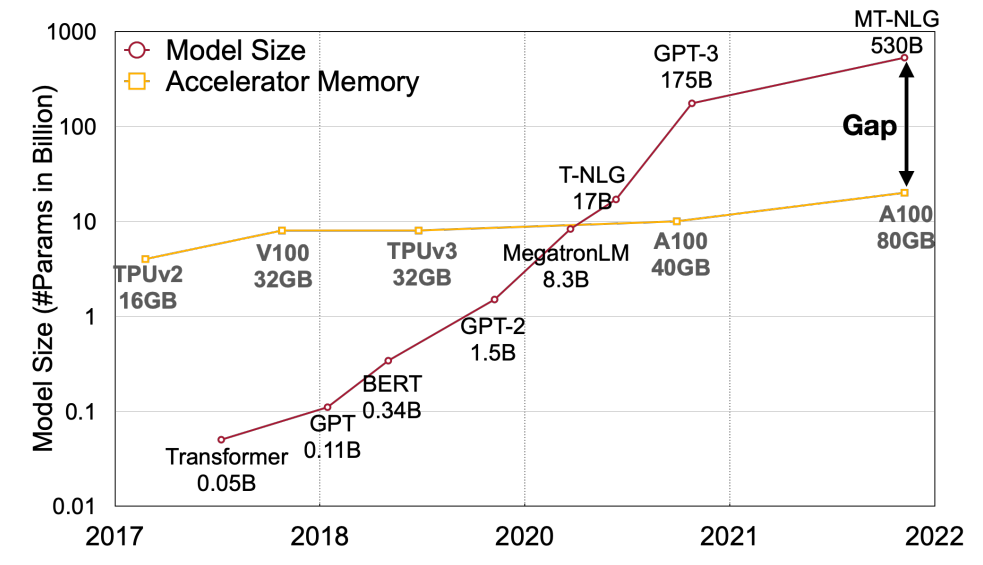
如何降低 memory 使用量將變的很關鍵, 因此 Activation-aware Weight Quantization (AWQ) 這篇文章就專注在 Weight Only Quantization (WOQ), 顧名思義就是 weight 使用 integer 4/3 bits, activations 仍維持 FP16.
因為 computation is cheap, memory is expensive.

Intel® Neural Compressor 有實作 WOQ 裡面有 AWQ

以下內容直接筆記 MIT SongHan 教授的課程內容[slides], [Video]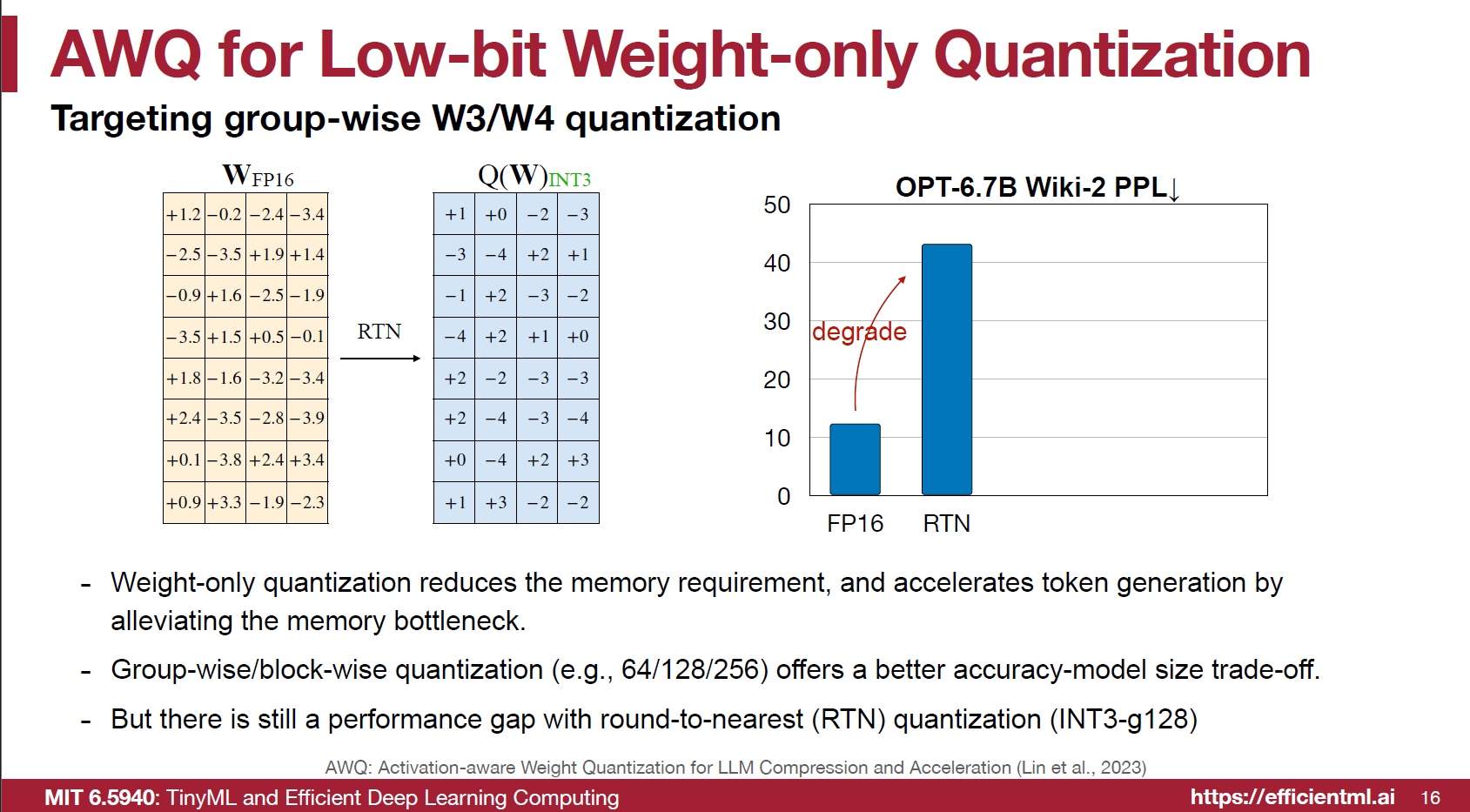


將 Weights quantize 到 4/3 bits 對 memory bandwidth 會有幫助, 但是直接使用 round-to-nearest (RTN) performance 會壞掉, 就算是使用 group-wise/block-wise 的方式也是沒用.
作者發現如果保留特定的 $1\%$ 的 weights 仍舊是 FP16 的話 (其餘都是 4/3 bits) 就可以保留住 performance. 如下圖顯示.

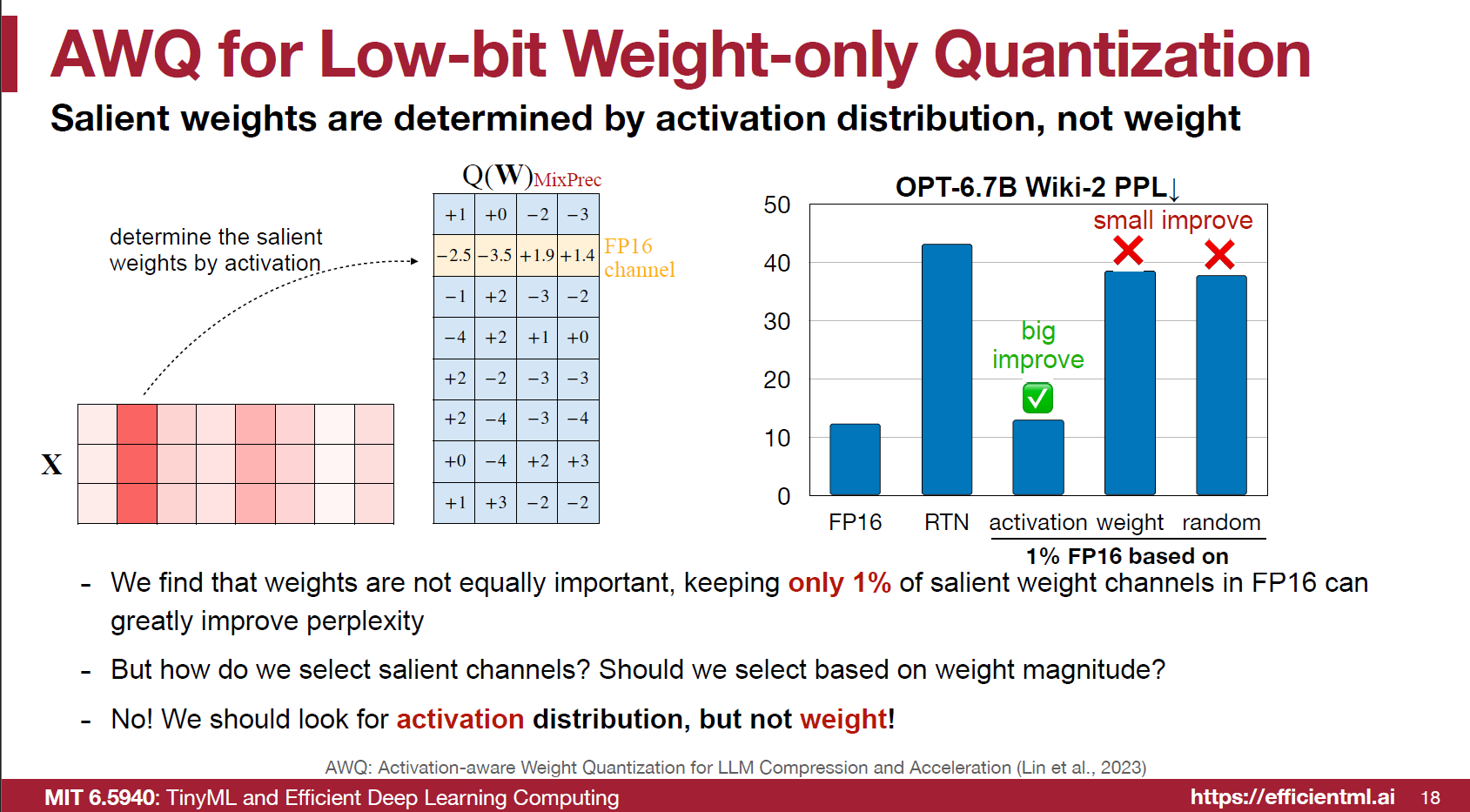特定的 weights 是那些呢? 因為 output activations 是 input activations 乗上 weights, 所以應該要看 activations 不能只單獨考慮 weights 大小.
還記得在 SmoothQuant 觀察到的現象嗎? activations 的 outliers 是以 per-channels 方式存在的, 也就是說 channels 之間差異可能很大, 但同一個 channel 內的值分佈都比較接近

圖中的 activation $X$ 的 row 表示 token (frame) 維度, column 表示 channel 維度. 所以對應到 weights 的話 input channel 就是 $W$ 的 row vectors.

要保留的那 $1\%$ 的 row vectors 的 weights 就是找對應 $X$ 的 column vectors 總和 magnitude 比較大的那些來保留. 見下圖 (b)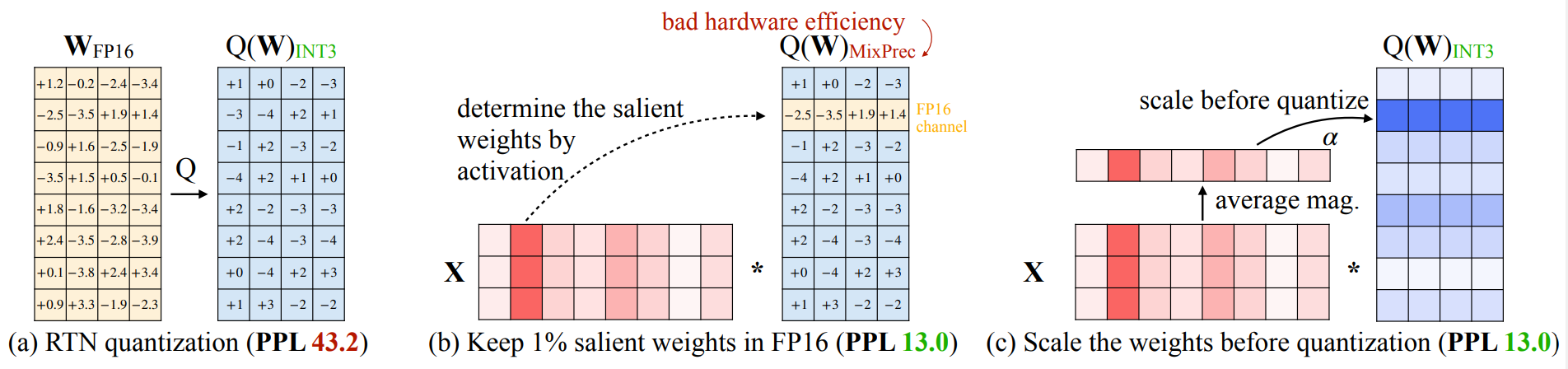
但能不能連 FP16 都不要, 最好全部都是 INT 因為這樣對 HW 比較友好.
作者發現透過一個簡單的 scaling 操作就有幫助 (其實概念一樣很像 SmoothQuant)
類似 SmoothQuant 的方式, 先對 quantization 之前的 Weights 乘上 scale $s$, 對應的在 input activations $X$ 除上 $s$, 如果沒有做 quantization 數學上就是等價.
下圖顯示對第 2 個 input channel 設定 $s=2$. 這麼做直接無損 performance.

但是為什麼呢?
原來 output activation 為

$$\hat{Y}=Q(\mathbf{w})\cdot \mathbf{x}=\Delta\cdot Round(\mathbf{w}/\Delta)\cdot \mathbf{x}$$ 現在改成:
$$\tilde{Y}=Q(\mathbf{w}\cdot s)\cdot \mathbf{x}/s=\Delta\cdot Round(s\mathbf{w}/\Delta)\cdot \mathbf{x}/s$$ 互相對比一下, 注意到由於 $\mathbb{E}[Round(\mathbf{w}/\Delta)]=\mathbb{E}[Round(s\mathbf{w}/\Delta)]=0.25$, 當 $s>1$ 的時候 $\tilde{Y}<\hat{Y}$, 使得 output activations 的 dynamic range 變小了, 等同於讓 outliers 變小更容易 quantization 了.

注意到這裡有個假設: $\Delta$ 不變的條件下. 這通常可以滿足, 因為實務上設定 $1 所以先對 salient weight channels 乘上 scale 後再 quantize, 然後再對 input activations 除 scale
下面這段 codes 是 SongHan 課程裡的 Lab4.ipynb
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
@torch.no_grad()
def pseudo_quantize_model_salient_weight_fp16(
    model, w_bit, q_group_size, input_feat
):
    for n, m in model.named_modules():
        if isinstance(m, nn.Linear):
            importance = sum(input_feat[n]).float() # importance is of shape [2048] or [8192] ...
            # Step 1: Find 1% of the salient weight channels according to importance (hint: use torch.topk())
            outlier_indices = torch.topk(importance,k=int(len(importance)*0.01))[1]
            assert outlier_indices.dim() == 1
            # Back up the values of the salient weight channels
            outlier = m.weight.data[:, outlier_indices].clone()
            m.weight.data = pseudo_quantize_tensor(m.weight.data, n_bit=w_bit, q_group_size=q_group_size)
            # Step 2: Restore the 1% salient weight channels to their original FP16 values
            m.weight.data[:, outlier_indices] = outlier

注意到 input_feat 使用 hook 事先對 calibration data 蒐集好的, 用來找出 $1\%$ 的那些 salient weight channels.
另外, 實際上我們不會對 input activation 除 scale, 而是將這個 scale 融進去前一層的 layer normalization weight 裡

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
@torch.no_grad()
def scale_ln_fcs(ln, fcs, scales):
    if not isinstance(fcs, list):
        fcs = [fcs]
    scales = scales.to(ln.weight.device)
    ln.weight.div_(scales)
    if hasattr(ln, 'bias') and ln.bias is not None:
        ln.bias.div_(scales)
    for fc in fcs:
        fc.weight.mul_(scales.view(1, -1))
    for p in ln.parameters():
        assert torch.isnan(p).sum() == 0
    for fc in fcs:
        for p in fc.parameters():
            assert torch.isnan(p).sum() == 0

如果是 Transformer 的 FFN layer, 則融進去前一層的 fc layer

1
2
3
4
5
6
7
8
9
10
11
12
13
14
@torch.no_grad()
def scale_fc_fc(fc1, fc2, scales):
    assert isinstance(fc1, nn.Linear)
    assert isinstance(fc2, nn.Linear)
    scales = scales.to(fc1.weight.device)
    # fc1.weight.div_(scales.view(-1, 1))
    fc1.weight[-scales.size(0):].div_(scales.view(-1, 1))
    if fc1.bias is not None:
        fc1.bias.div_(scales.view(-1))
    fc2.weight.mul_(scales.view(1, -1))
    for p in fc1.parameters():
        assert torch.isnan(p).sum() == 0
    for p in fc2.parameters():
        assert torch.isnan(p).sum() == 0

我有點疑問, 做 AWQ 的 order 是不是有影響? 譬如後面的 layer 做 AWQ 的時候會讓前一個 layer 除上 scale, 但如果前一個 layer 已經先做過 AWQ 了, 那不就白做了? (教授課程的作業裡面會讓我有這種疑問, 但課程作業就這樣設計了, 感覺是沒影響. 還是因為不會動到同一個 channel?) 這個疑問待後續解決.

最後, 比較好的做法是用一個 calibration data 做 $s$ 的 grid search. 而 search 的目標函式為 output activation 的 quantization error:

$$\begin{align} 𝐋(\mathbf{s})=\lVert Q(\mathbf{W}\cdot \mathbf{s}) (\mathbf{s^{-1}} \cdot \mathbf{X}) - \mathbf{W}\mathbf{X} \rVert, \quad\mathbf{s}= \mathbf{s_X}^{\alpha}\\ \mathbf{s}^* = \text{argmin}_{\mathbf{s}} 𝐋(\mathbf{s}),\quad \alpha^*=\text{argmin}_{\alpha} 𝐋(\mathbf{s_X}^{\alpha}) \end{align}$$ 其中 $\mathbf{s_X}$ 是 input activation 的 magnitude, $\alpha\in[0,1]$, $0$ 表示沒有 scale; $1$ 表示最強的 scale. Grid search 是對 $\alpha$ 做.

最後實驗結果顯示對 LLMs, OpenFlamingo 做到 4/3bits 的 weights quantization 很有效: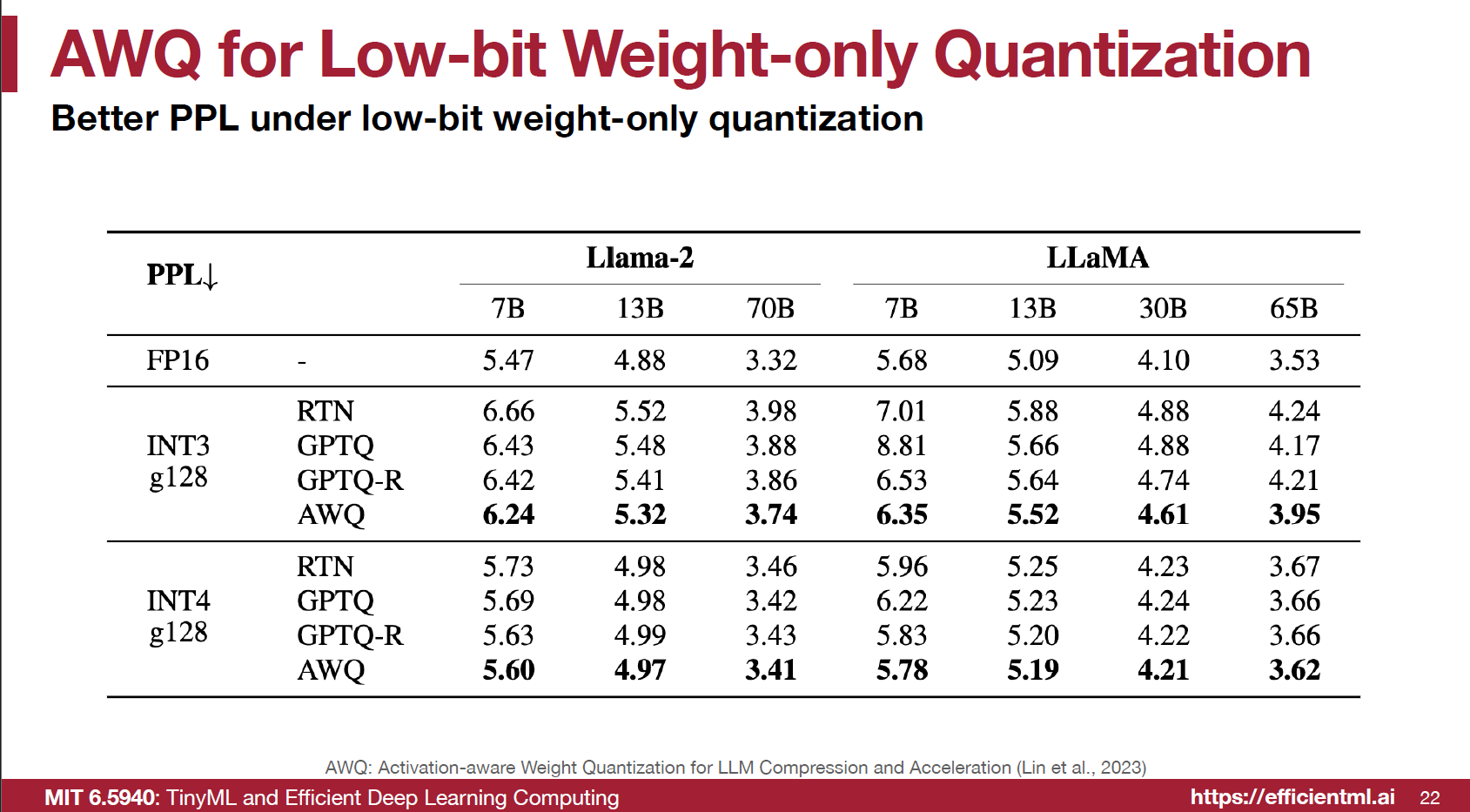


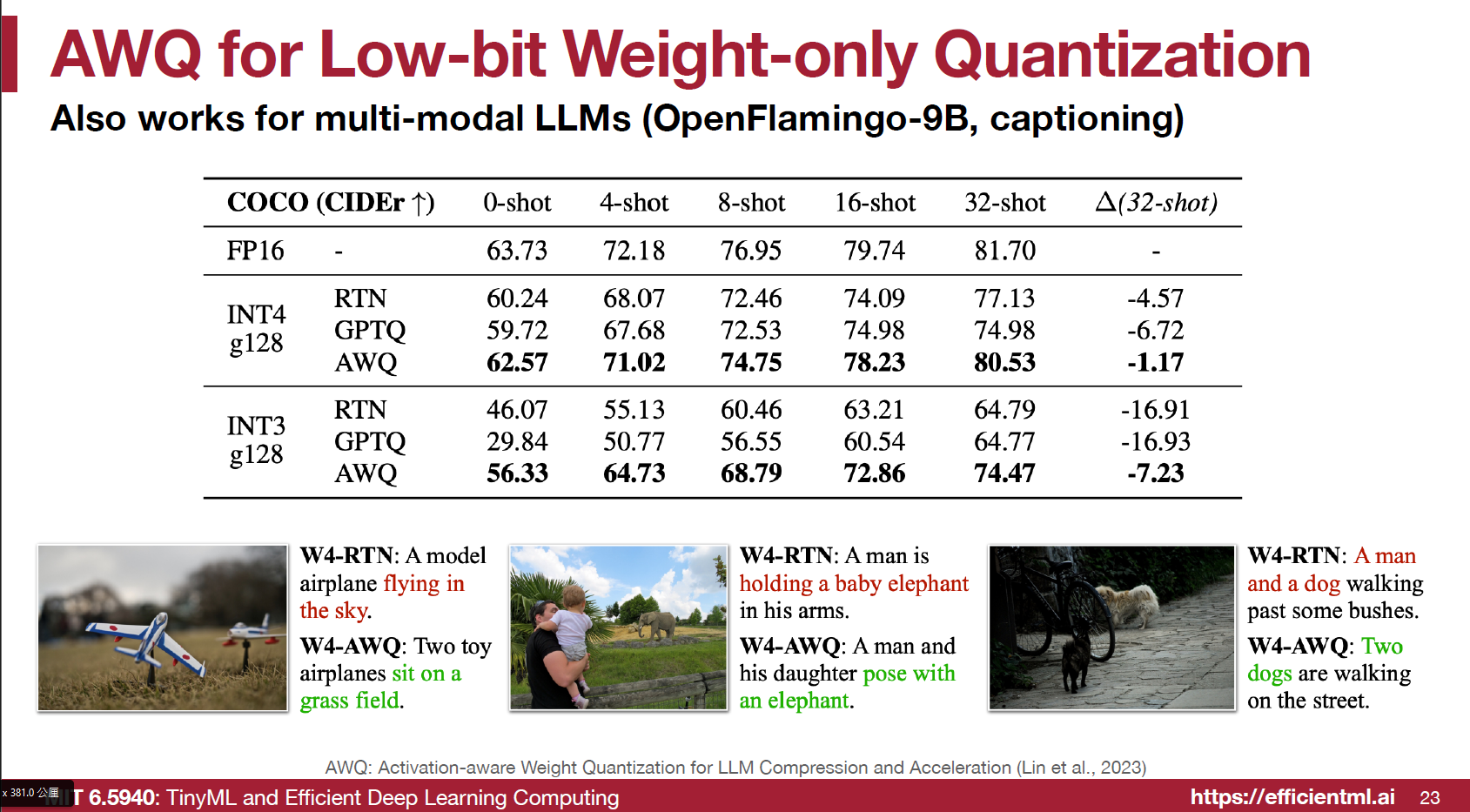
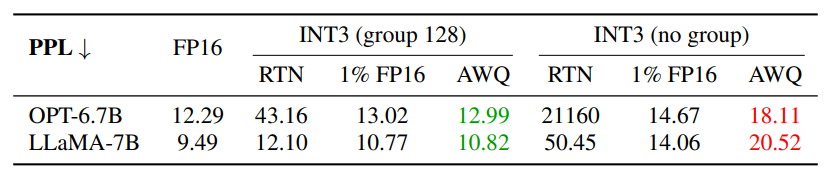這裡實驗如果是用 per-channel 會效果不好, 所以建議搭配 per-vector 或稱 per-group quantization.

References

  1. AWQ: Activation-aware Weight Quantization for LLM Compression and Acceleration, [arxiv]
  2. MIT HAN Lab, Course: TinyML and Efficient Deep Learning Computing [slides], [Video]
  3. Intel® Neural Compressor‘s WOQ