這是 MIT SongHan 教授實驗室的論文, 使用 PTQ 對 LLM 做到 W8A8 的量化, 由於 activations 會有比較大的 outliers 導致 quantization 後損失較大, 而一般 weights 的 outliers 很少, 因此透過一些等價的轉換將 activations 的 scale 縮小並放大 weights 的 scale, 使得 activations 變的較容易 quant 而 weights 仍然容易 quant. 如論文的圖顯示:
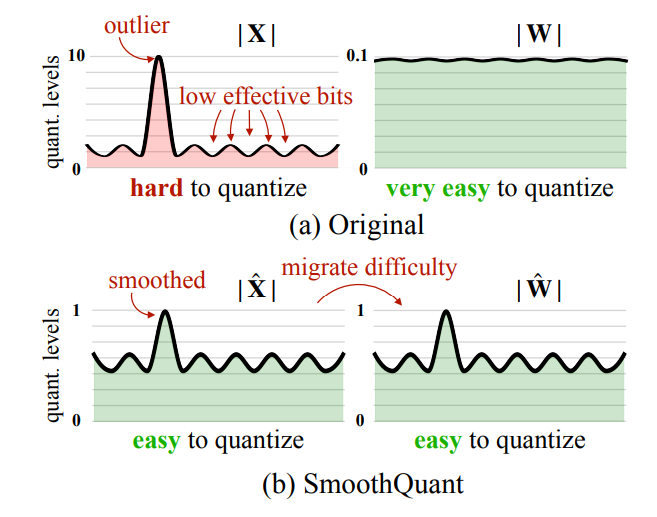
Quantization Granularity
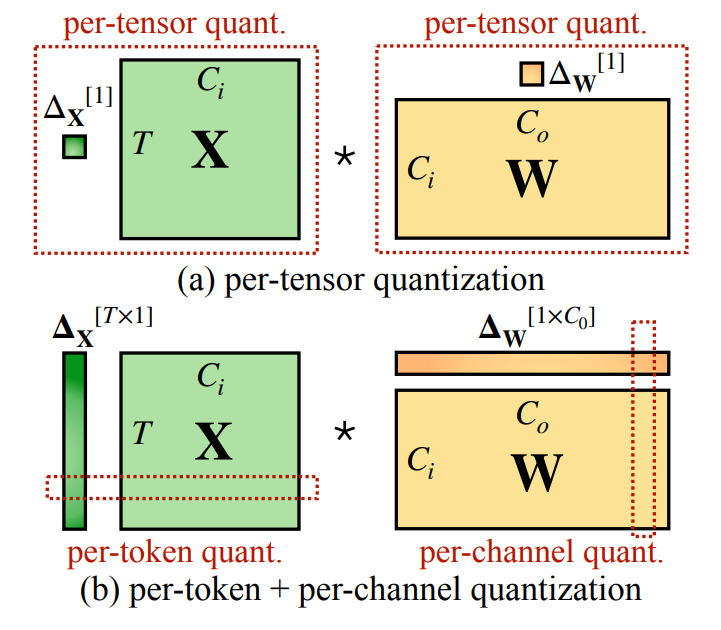
先說明一下不同 quantization granularity, 其中
- Activation $X$ 的 row 是 token 維度, col 是 input channel 維度.
- Weight $W$ 的 row 是 input channel 維度, col 是 output channel 維度.
- $\Delta_X$, $\Delta_W$ 分別指的是 activation $X$ 和 weight $W$ 的量化參數 (scales, zero points)
可以看到 per-tensor 指的是整個 matrix 共享同一組量化參數
而 per-token (per-frame) 則表示 $X$ 同一個 row 共享同一組量化參數; 同理 per-channel 是對 $W$ 的 output channel 同一個 column 共享同一組量化參數
GEMM 在對 $XW$ 矩陣乘法並行加速的時候, 對 $X$ 採用 row-major, $W$ 採用 col-major 則 output 每個 element 都可以獨立運算, 所以可以並行.
這邊思考一個問題, 如果 $X$ 採用 per-channel (同一個 column 共享同一組量化參數), 在做 GEMM 時, $X$ 的一個 row 裡面每個元素都需要採用不同的量化參數, 這會破壞掉 GEMM 並行的好處.
因此一般來說 $X$ 採用 per-token, 而 $W$ 採用 per-channel (output channel) 對 GEMM 比較友善.
Motivation
實際觀察 $X$ 的分佈, 發現數值分佈的特性是 channel 內差異不大, 但 channel 之間的差異很大. 因此對 $X$ 來說採用 per-channel quantization 才是比較合適的, 但是從上一段我們知道 $X$ 採用 per-token 對 GEMM 才會比較友善. 那該怎麼辦? 這就是 SmoothQuant 要做的事, 降低 $X$ 的 outliers 使得可以仍採用 per-token.
如論文 Figure 4, 和講義說的
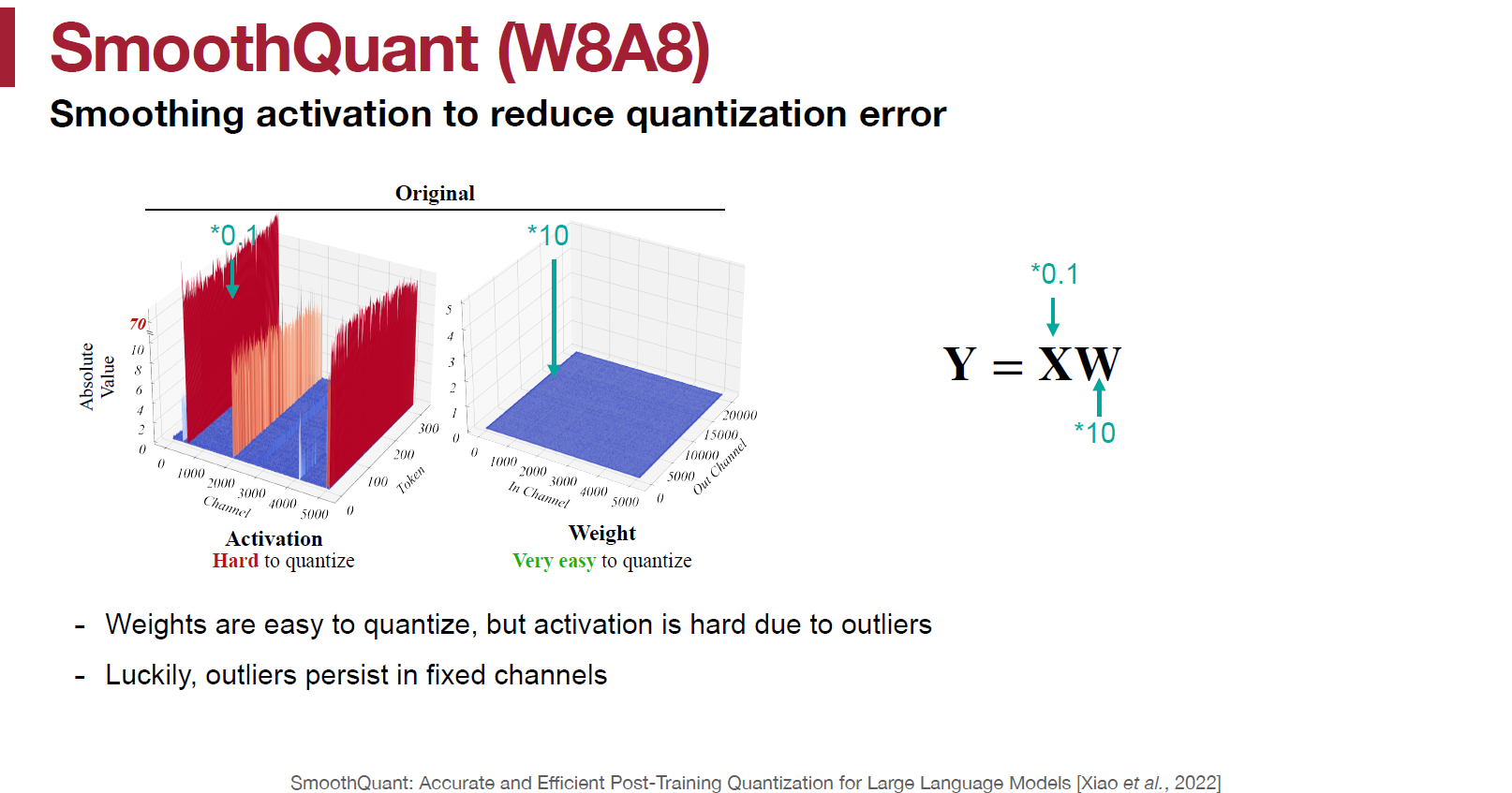
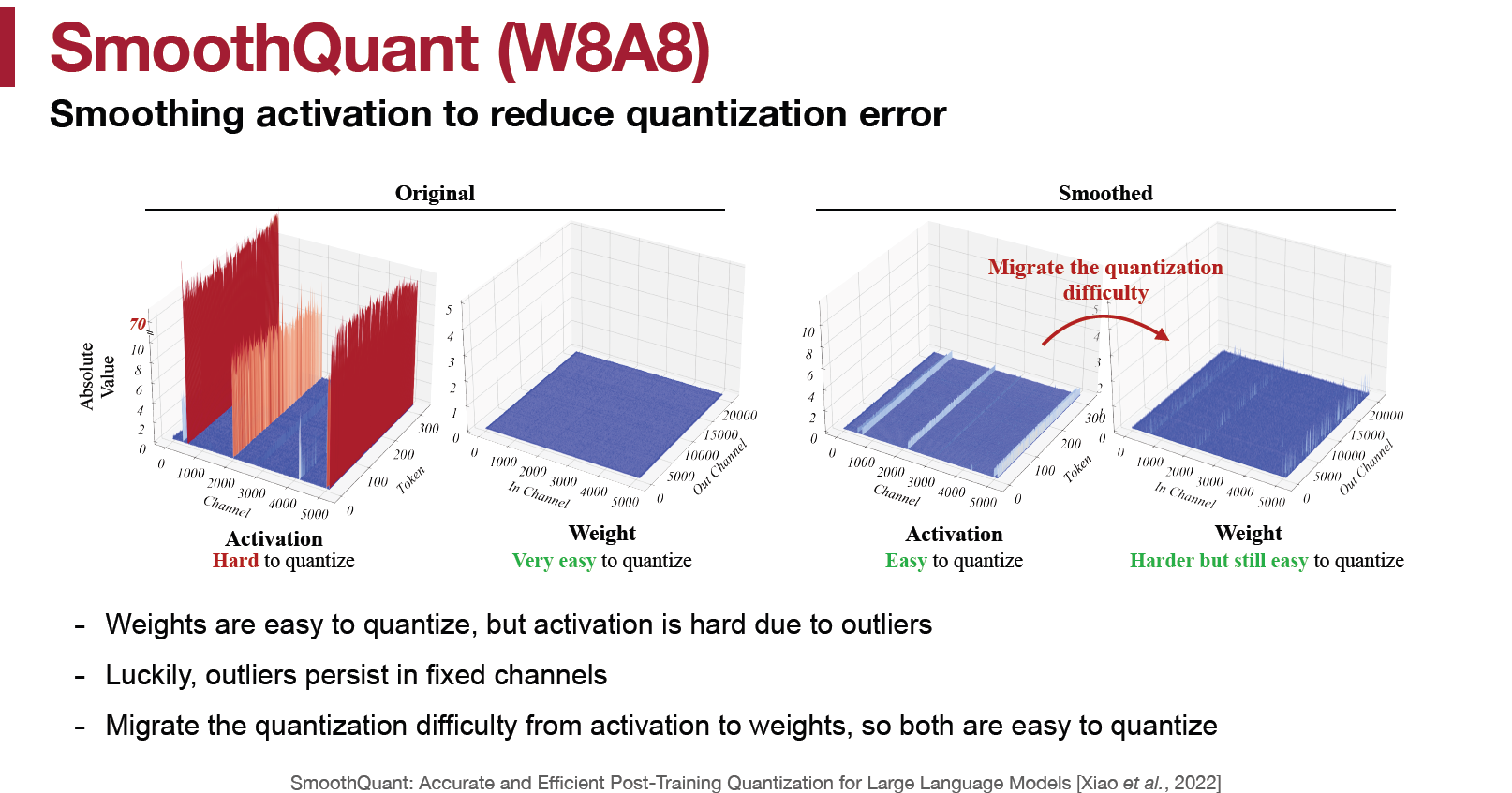
SmoothQuant 方法
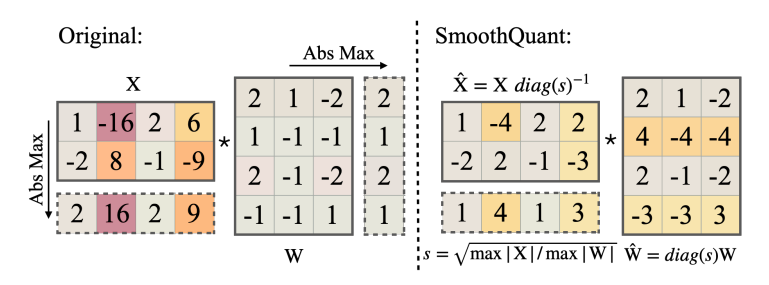這些 activations $X$ 的 outliers 都存在於某幾個特定的 channels, 跟哪一個 tokens 維度無關. 所以我們如果使用 per-channel quant, 則可以對 channels 的 scales 對應做個分配.
其中 $X diag(s)^{-1}$ 可以把 $diag(s)^{-1}$ 融合進去前一層的 layer normalization 參數裡頭. 而 $diag(s)W$ 直接融進去 $W$ 的 scaling factor 裡.
選擇 channel 的 re-scaling factor 如下:
$$s_j=\max(|X_j|)^\alpha/\max(|W_j|)^{1-\alpha}$$ 通常 $\alpha=0.5$ 是個很好的選擇 (控制 activation 還是 weight 量化難度的 trade-off), 但如果遇到 activation 的 outlier 比重占比較多的話 ($\sim30\%$), 可以選 $\alpha=0.75$.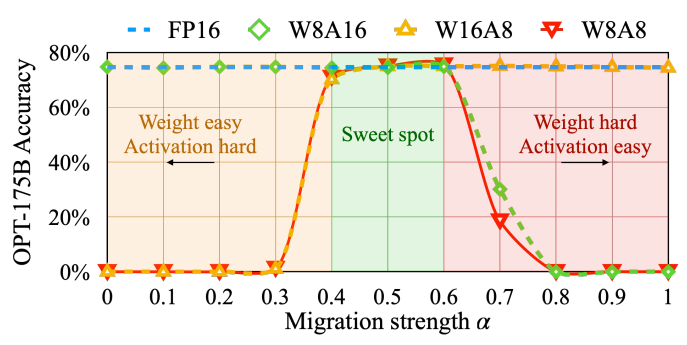
最後論文採用的 format 為:
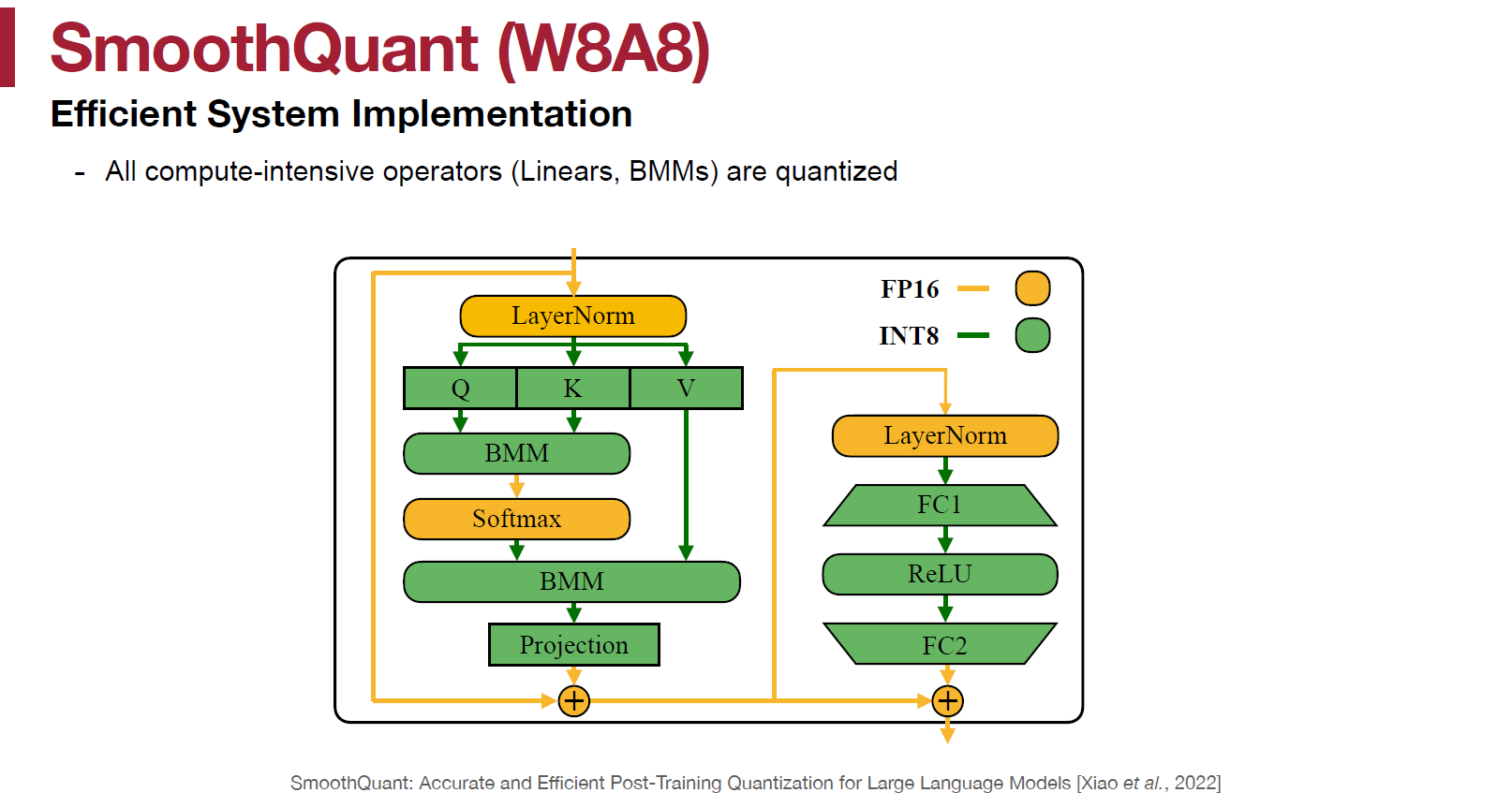SmoothQuant 透過把 quantization 困難移轉到 weight 上, 所以 $X$ 仍可以使用 per-token(frame) 或甚至 per-tensor quant, 同時也不影響 GEMM 加速.
實驗結果
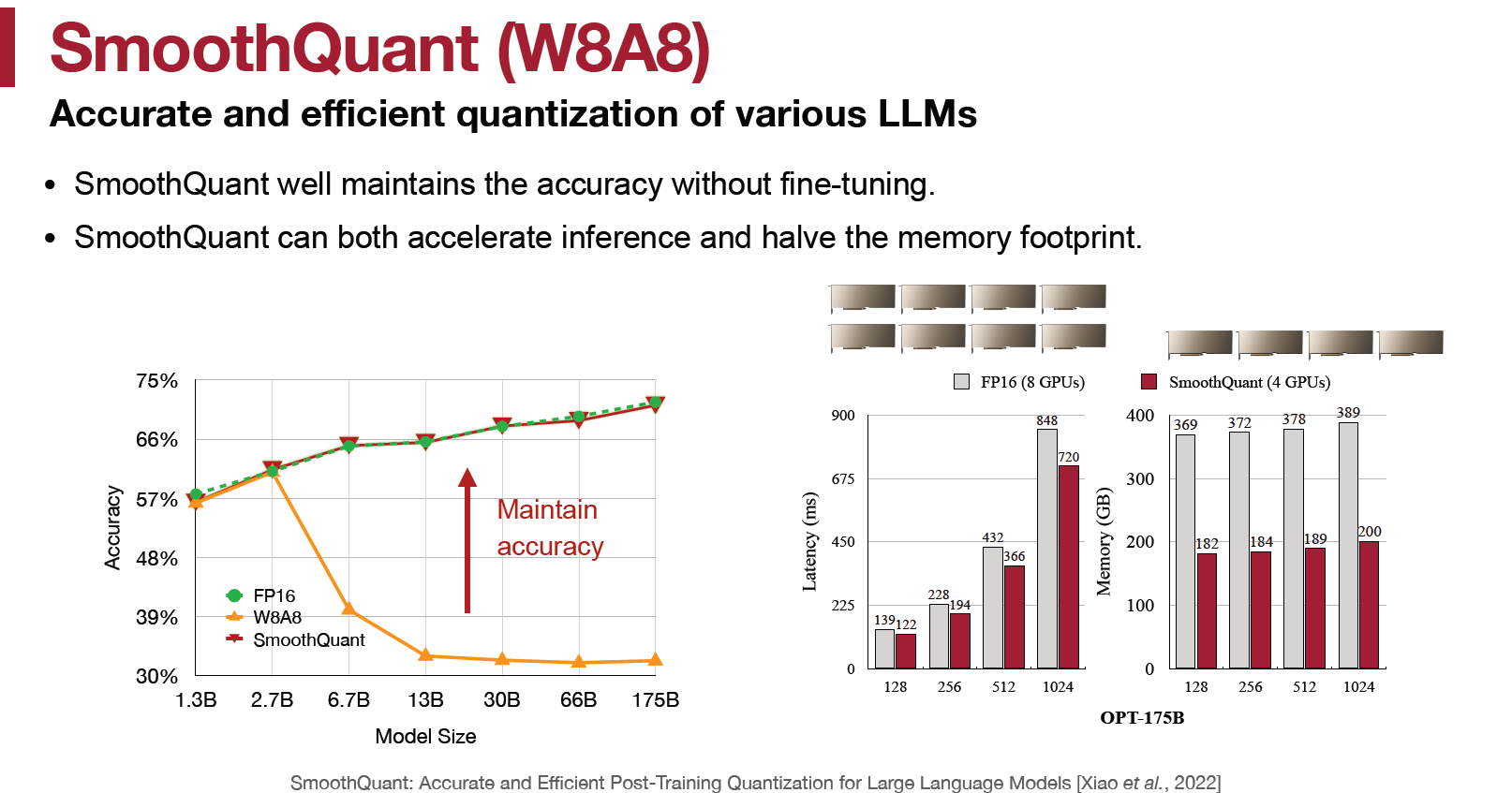對 OPT-172B 能有效恢復 acc to FP16 水準, 同時需要的 GPU 減半, latency 也減少. 然後對更大的 model 也同樣有效, like MT-NLG 530B
對 Llmma 同樣也是, 主要想看一下 SwishGLU, RoPE 這種不一樣的 op 對於 SmoothQuant 的假設是否一樣成立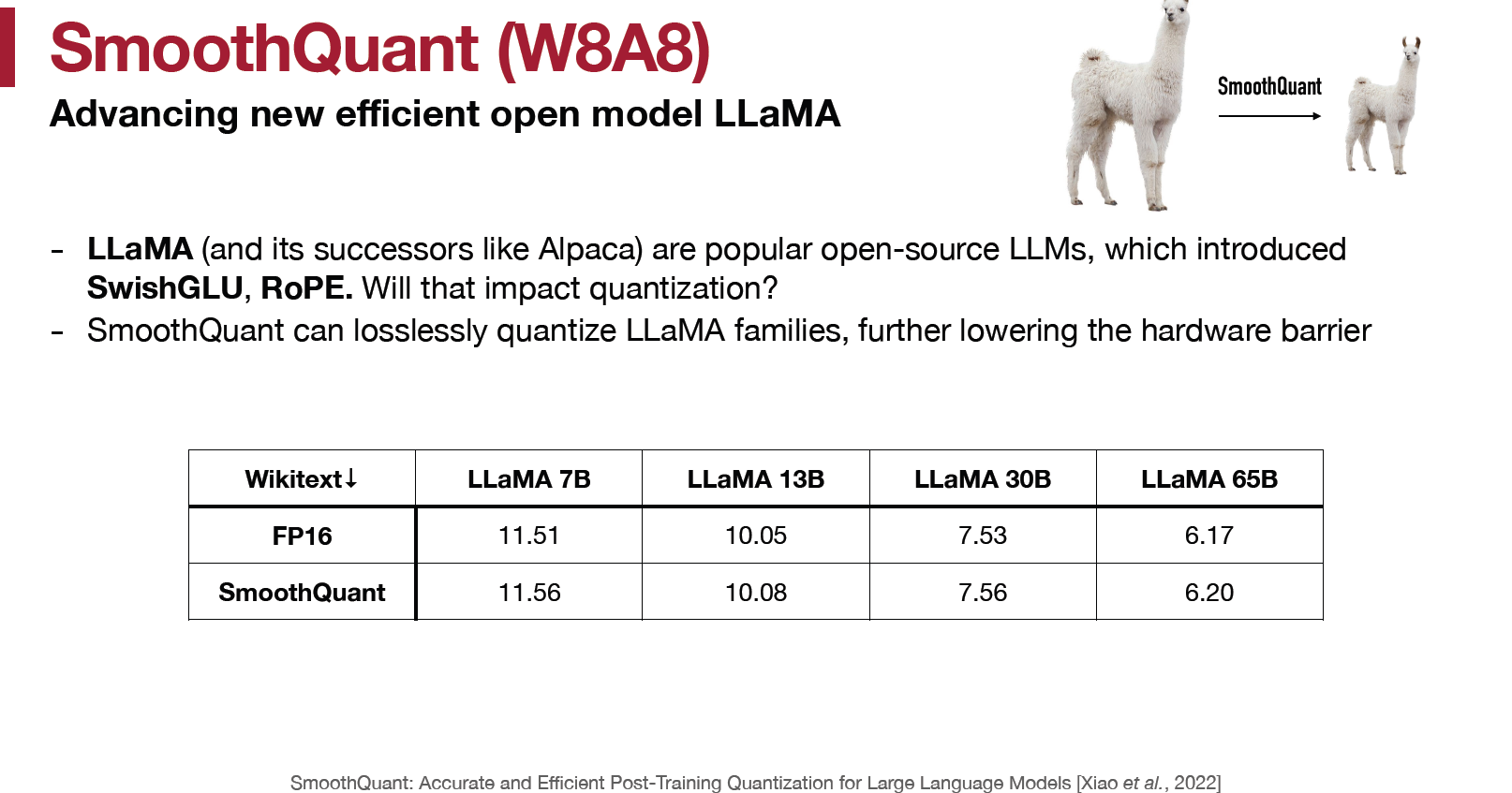
References
- SmoothQuant: Accurate and Efficient Post-Training Quantization for Large Language Models, [arxiv]
- MIT HAN Lab, Course: TinyML and Efficient Deep Learning Computing [slides], [Video]