Speculative Decoding 詳讀 (上)

---

這是 Transformer inference 的加速, 有人猜測 GPT-4 也使用這個方法: https://archive.ph/2RQ8X
Speculative decoding 做到了不影響準確率情況下直接加速 (不改 model 架構, 不 fine tune, 不做 PTQ 等)
這麼神奇的操作就是利用了一個小模型來先跑一些 tokens, 再由原來的大模型評估或修正.
論文顯示 LLM 效果無損直接可提速 2~3 倍, 讓我們看下去

Motivation

---

使用 SongHan 教授的課程 slides.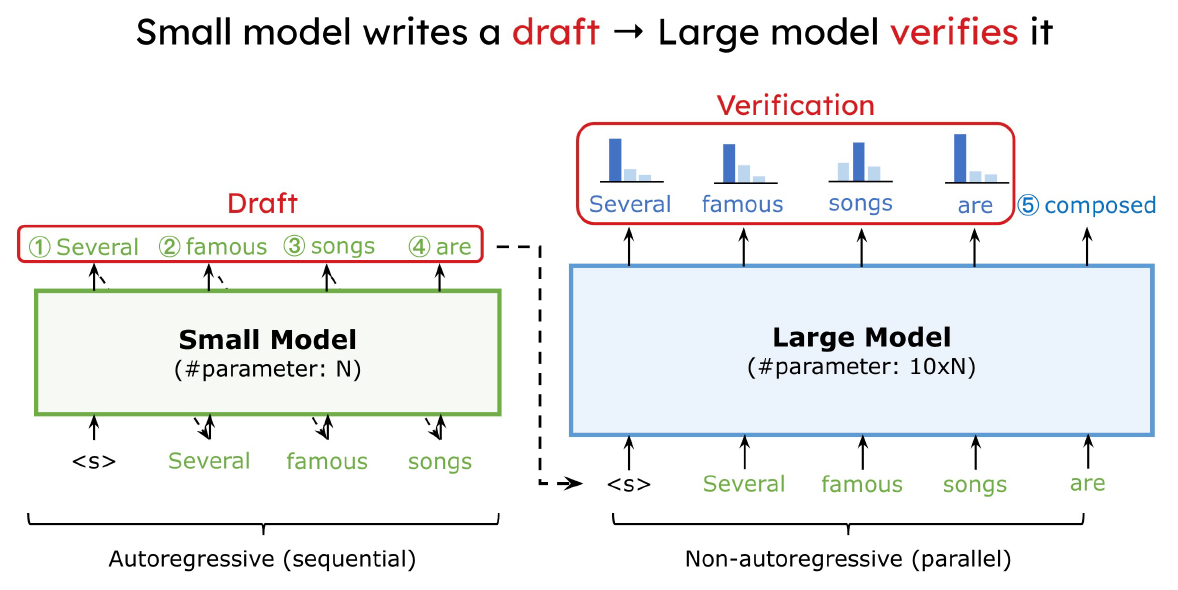
利用 small model 先提出一些 draft tokens, 然後用 large model 來驗證. 如果大部分都接受, 直覺上可以省去很多 large model 的呼叫次數, 因此加速. 方法十分簡單, 不過其實魔鬼藏在細節裡, 跟原本只使用 large model 的方法比較有幾個問題要回答:
 A. 速度的分析: 加速到什麼程度? 跟小模型的速度和準確度有關聯嗎? (想像如果 draft 一直被拒絕, 則小模型都是多跑的)
 B. 運算量的分析: Operation 數 (計算量) 也會減少嗎? 還是會增加?
 C. Memory bandwidth 的分析: 會減少還是增加?
 D. Performance 能維持住嗎 (PPL, WER, BLEU, … 端看 model task 是什麼): 還是會有 degrade?
Google 這篇論文很精彩的理論分析了以上所有問題, 並有實務驗證
先破題, performance (PPL, WER, BLEU, …) 可以保證維持住! 我們等到本篇筆記最後在討論, 以下會先討論算法流程、加速和運算量的分析.

Speculative Decoding 算法流程

---

使用論文的術語, 例如上面說的 small model 改稱 approximation model, large model 改稱 target model, draft 用 proposal tokens.
Approx. model, $M_q$, 用 auto-regressive 方式產生 $\gamma$ 個 proposal tokens $\{x_1,...,x_\gamma\}$ 和機率分布 $\{q_1(x),...,q_\gamma(x)\}$, 接著把 proposal token 結合上次一的 prefix tokens (但這裡我們為了簡化先忽略 prefix) 給 target model, $M_p$, 做一次 non-autoregressive forward (parallel) 跑出機率分布 $\{p_1(x),...,p_\gamma(x),p_{\gamma+1}(x)\}$.
比較 $p(x),q(x)$ 來決定是否接受 proposal tokens, 如果 $p(x)\geq q(x)$ 則採用 $M_q$ 的 proposal token, 否則有 $p(x)/q(x)$ 機率仍會接受 proposal token, 有 $1-p(x)/q(x)$ 的機率要根據修改的機率分布 $p'(x)=norm(\max(0,p(x)-q(x)))$ 重新採樣 token.
另外如果所有 $\gamma$ 個 proposal tokens 都被接受了, 則直接從 target model 的 $p_{\gamma+1}(x)$ 採樣token.
以上為一個 step or run, 重複直到句子產生結束.
參考下圖: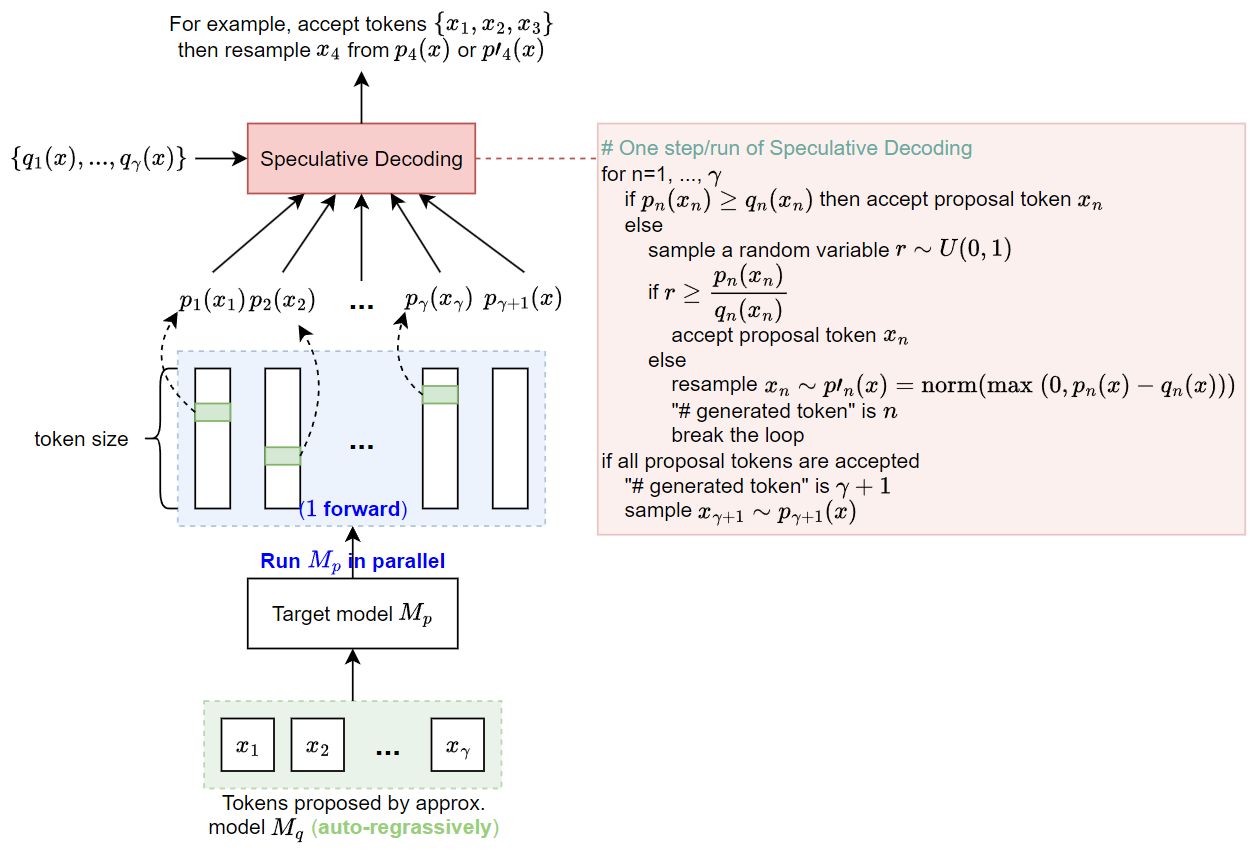

1. 注意到 $\{p_1(x),...,p_\gamma(x),p_{\gamma+1}(x)\}$ 是一次 forward 就跑出來的, 相比 auto-regressive 的方式要跑 $\gamma$ 次 forward (load $\gamma$ 次 model 參數), 現在只需要 load 一次參數(and kv-cache)因此可以節省 memory bandwidth. 但注意到這兩種方式的總計算量是不變的.
2. 一般來說 $M_p$ 的輸入會結合上一次 decode 的 tokens (稱 prefix) 加上 $M_q$ 的 proposal tokens 當輸入, 但是這些 prefix 由於上一次 decode 時 forward 過, 在使用 kv-cache 的技巧下可以省略計算.

速度和運算量的初步分析

---

先定義 $\mathbb{E}(\# \text{generated tokens})$ 表示 speculative decoding 平均一個 run 可以產生多少”有效” tokens (因為不是所有 proposal tokens 都會被接受)

推論速度 (Walltime) 變化?

每一個 run 需要的時間為 $Tc\gamma + T$, 其中 $T$ 是跑一次 target model 所花的時間, $c$ (cost coefficient) 是 approx. model 跟 target model 的時間比 (愈小表示 approx. model 跑愈快). 所以:
 - speculative decoding 花了 $Tc\gamma + T$ 的時間產生 $\mathbb{E}(\# \text{generated tokens})$ 個 tokens
 - 只用 target model 花了 $T$ 的時間產生 $1$ 個 token
因此只要知道 $\mathbb{E}(\# \text{generated tokens})$ 我們可推得使用 speculative decoding 的速度提升 (walltime improvement):

$$\begin{align} \text{Walltime Improvement}=\frac{\text{Speculative decoding (tokens per time)}} {M_p\text{ decoding (tokens per time)}}\\ =\frac{\mathbb{E}(\#\text{generated tokens})/(Tc\gamma+T)} {1/T}\\ =\frac{\mathbb{E}(\#\text{generated tokens})}{(c\gamma+1)} \end{align}$$ 數值愈高表示使用 speculative decoding 加速愈多

運算量的變化?

定義 $\hat{T}$ 是 target model ”per token” 的運算量, 而 $\hat{c}$ 是 approx. model 跟 target model 的運算量比. 每一次的 run, approx. model 會 auto-regressive $\gamma$ 次, 所以是 $\hat{T}\hat{c}\gamma$, 而 target model 會對 $\gamma$ 個 proposal tokens parallel 去跑 $1$ 次, 注意到雖然是 parallel, 但總運算次數是正比於 proposal token 數量的 (只是並行跑), 所以花的運算量為 $\hat{T}(\gamma+1)$. 所以:
 - speculative decoding 花了 $\hat{T}\hat{c}\gamma+\hat{T}(\gamma+1)$ 運算量產生 $\mathbb{E}(\# \text{generated tokens})$ 個 tokens
 - 只用 target model 花了 $\hat{T}$ 的運算量產生 $1$ 個 token
同樣只要知道 $\mathbb{E}(\# \text{generated tokens})$ 我們可推得運算量的變化.
PS: 注意到 prefix tokens 不會花到運算量因為 kv-cache 技巧, 所以考慮的時候可以忽略.

$$\begin{align} \#\text{OPs Increasing Ratio}=\frac{\text{Speculative decoding (\#OPs per token)}}{M_p\text{ decoding (\#OPs per token)}} \\ =\frac{(\hat{T}\hat{c}\gamma+\hat{T}(\gamma+1))/\mathbb{E}(\#\text{generated tokens})}{\hat{T}/1} \\ = \frac{\hat{c}\gamma+\gamma+1}{\mathbb{E}(\#\text{generated tokens})} \end{align}$$ 數值愈高表示使用 speculative decoding 要花愈多 OPs 數 (運算量愈高)

平均生成的 Tokens 數

---

Proposal Tokens 被接受的機率 $\beta_t,\alpha$

綜上所述, 需要先計算 $\mathbb{E}(\# \text{generated tokens})$, 等同於要計算 token 的 accept 機率我們才能得知速度以及運算量的變化.
將 proposal token $x_t\sim q(x|x_1,...,x_{t-1})=:q_t(x)$ 被 speculative decoding 接受的機率定義為 $\beta_t$.
數學上可以麼表達 (為了清楚, 在沒有混淆情況下省略下標 $t$):

$$\begin{align} \beta = \mathbb{E}_{x\sim q(x)} \left\{ \begin{array}{rl} 1 & q(x)\leq p(x) \\ {p(x)\over q(x)} & q(x)>p(x) \end{array} \right.\\ = \mathbb{E}_{x\sim q(x)} \min\left(1, {p(x)\over q(x)}\right)=\sum_x\min(p(x),q(x)) \end{align}$$ 注意到 $\beta_t$ 跟時間 $t$ 相關, 為了簡化, 論文假設 $\beta_t,\forall t$ 都是從一樣的 distribution sample 的 random variables.
所以可以簡化為定義
$$\begin{align} \alpha := \mathbb{E}_t[\beta_t]=\sum_t\sum_x\min(p_t(x),q_t(x)) \end{align}$$ 論文計算了不同 $M_q,M_p$ 之間的 $\alpha$. 可以看到 $M_q$ model size 愈大 $\alpha$ 愈高, 顯示愈匹配.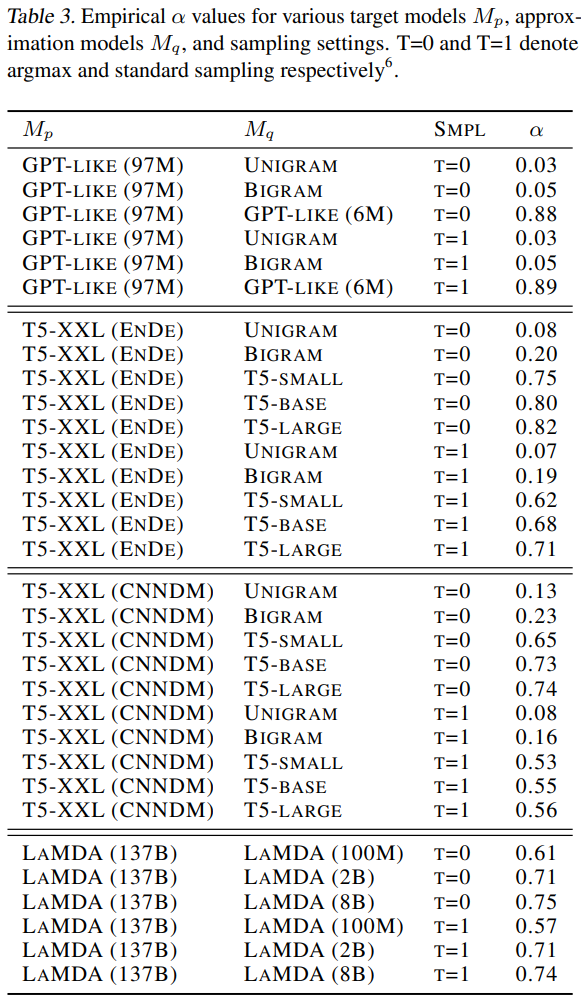
有趣的是, 以T5系列的 models 來看, $M_q$ 選擇 bi-gram 這種非常簡單的 LM $\alpha$ 還有 $0.2$, 代表 bi-gram model 的 proposal tokens 平均5個有1個會被接受.

如果 approx. model 跟 target model 愈匹配的話, accept rate ($\beta_t,\alpha$) 就會愈高
因此 $\beta_t$ 或 $\alpha$ 可以看成是小模型跟大模型的匹配程度.

但是再繼續之前, 我們必須先回顧一下幾何分佈

Geometric distribution with capped number of trails

考慮一次測試 (trail) 的成功機率為 $\theta$, 最多測試 $n$ 次 trails, random variable $X$ 代表要花多少次的 trails 才會至少成功一次. 注意到如果前 $n-1$ 次都 fail, 則強制最後第 $n$ 次一定成功.
前 $n-1$ 次至少會 success 一次所需花的 trails 次數期望值為:
 $1\times\text{第一次就成功的機率} + 2\times\text{第二次才就成功的機率} + ... + (n-1)\times\text{第}(n-1)\text{次才成功的機率}$

$$\theta\sum_{x=1}^{n-1}x(1-\theta)^{x-1}=\theta \sum_{x=1}^{n-1}\left( -\frac{d}{d\theta}(1-\theta)^x \right) \\ =-\theta\frac{d}{d\theta}\left(\sum_{x=1}^{n-1}(1-\theta)^x\right) = -\theta\frac{d}{d\theta}\left( \frac{(1-\theta)(1-(1-\theta)^{n-1})}{1-(1-\theta)}\right) \\ = -\theta\frac{d}{d\theta}\left( \frac{(1-\theta)-(1-\theta)^n}{\theta} \right) \\ =-\theta\frac{\theta(-1+n(1-\theta)^{n-1})-(1-\theta)+(1-\theta)^n}{\theta^2}\\ =\frac{\theta-n\theta(1-\theta)^{n-1}+(1-\theta)-(1-\theta)^n}{\theta}$$ 加上 $n-1$ 次都 fail, 所以強制最後第 $n$ 次一定 success 的機率為 $(1-\theta)^{n-1}$ 並乘上次數 $n$, 因此總體期望值為:
$$\mathbb{E}\left[X\right]= \frac{\theta-n\theta(1-\theta)^{n-1}+(1-\theta)-(1-\theta)^n}{\theta} + n(1-\theta)^{n-1} \\ =\frac{1-(1-\theta)^n}{\theta}$$

計算平均生成的 tokens 數

$\mathbb{E}(\# \text{generated tokens})$ 相當於要計算試驗次數有上限 (capped number of trails) 的 geometric distribution 的期望值.
對應到 speculative decoding 的問題裡 $\theta=1-\alpha$, 且試驗次數最多 $\gamma+1$ 次., 因此將 $\theta = 1-\alpha$, $n=\gamma+1$ 代入得到:

$$\begin{align} \mathbb{E}[\#\text{generated tokens}]=\frac{1-\alpha^{\gamma+1}}{1-\alpha} \end{align}$$ 論文把小模型與大模型的匹配程度 $\alpha$ 跟 (10) 的關係畫出來: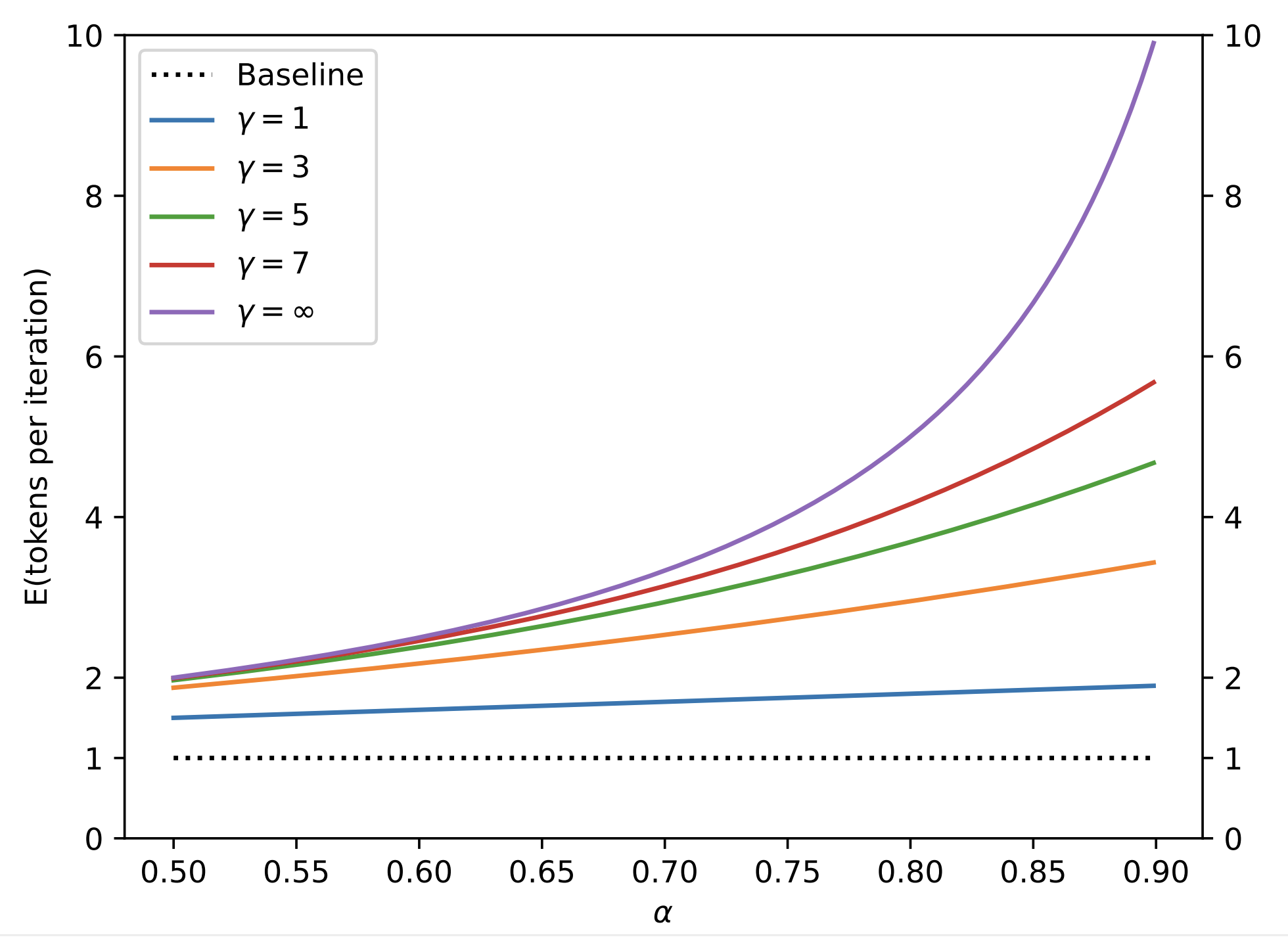
我們發現 $M_q$ 與 $M_p$ 愈匹配的話, speculative decoding 一次 run 產生的 tokens 愈多 (很合理, 因為被接受的機率愈高)
產生的 tokens 上限就是 $\gamma+1$ ($\gamma$ 個 proposal tokens 全被接受加上最後一個 $M_p$ 產生的 token)

待續 …

References

---

1. Google: Fast Inference from Transformers via Speculative Decoding [arvix]
2. DeepMind: Accelerating Large Language Model Decoding with Speculative Sampling [arxiv]
3. Speculative_sampling.drawio
4. Speculative Decoding 詳讀 (下)