接續上一篇
現在我們可以真正的來探討以下問題了:
A. 速度的分析: 加速到什麼程度? 跟小模型的速度和準確度有關聯嗎? (想像如果 draft 一直被拒絕, 則小模型都是多跑的)
B. 運算量的分析: Operation 數 (計算量) 也會減少嗎? 還是會增加?
C. Memory bandwidth 的分析: 會減少還是增加?
D. Performance 能維持住嗎 (PPL, WER, BLEU, … 端看 model task 是什麼): 還是會有 degrade?
A. 速度的分析
將上一篇的公式 (10):
$$\mathbb{E}[\#\text{generated tokens}]=\frac{1-\alpha^{\gamma+1}}{1-\alpha}$$ 代入上一篇的公式 (3)
$$\text{Walltime Improvement}=\frac{\mathbb{E}(\#\text{generated tokens})}{(c\gamma+1)}$$ 我們得到
$$\begin{align}
\text{Walltime Improvement}=\frac{1-\alpha^{\gamma+1}}{(c\gamma+1)(1-\alpha)}
\end{align}$$ 先分析一下 walltime, 我們設定 $c=[0.1,0.4,0.8]$, $\gamma=[3, 5, 7]$ 觀察 walltime V.S. $\alpha$ 的變化
回顧一下 $c$ 表示 approx. 跟 target model 之間的速度比, 愈小表示 approx. model 速度愈快. $\gamma$ 表示 proposal tokens 的數目. 而 $\alpha$ 可以代表 approx. and target models 之間的匹配程度 (愈高表示愈匹配, proposal token 被接受的機率愈高)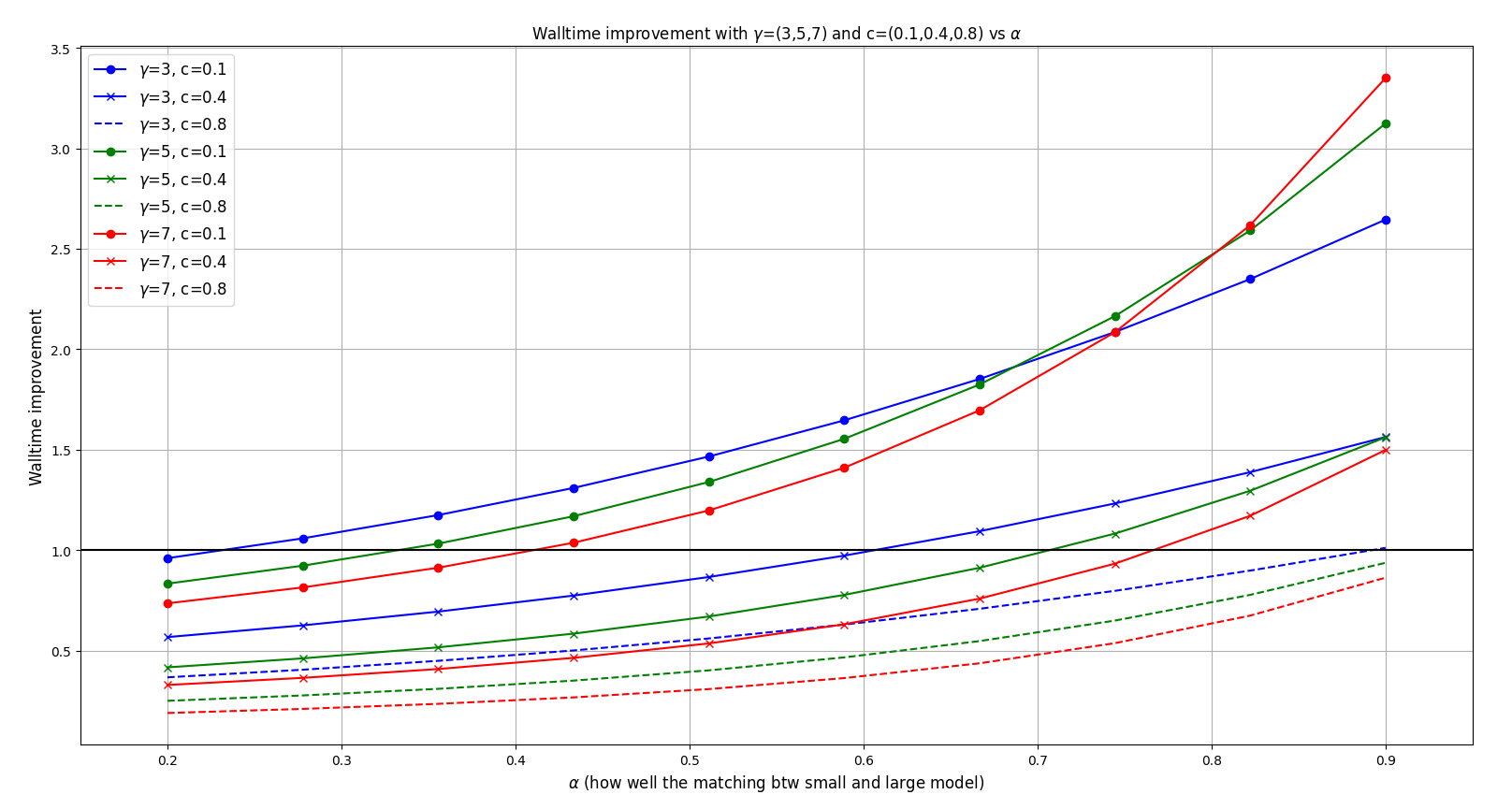
觀察到幾點 (注意到比黑色實線小, walltime improvement $<1$, 代表沒有加速到):
1. 如果 $\alpha$ 愈大, 表示大小模型之間愈匹配可以加速愈多
2. $c$ 愈小 (小模型速度愈快) 則加速愈多
3. $\gamma$ 則不一定 (看$c=0.1$ 的 case), 所以可能要找出最佳值
那有沒有可能 $\gamma$ 不管怎麼找都找不出 walltime improvement 至少 $>1$ 呢? 這種情況就不用花力去氣找了.
論文 Corollary 3.9. 說明 $\alpha>c$ 的情況則存在 $\gamma$ 使得會有加速好處. 加速效果至少是 $(1+\alpha)/(1+c)$ 倍.
所以 approx. and target models 的選擇就先考慮 $\alpha>c$ 的配對, 然後對 $\gamma$ 找出最佳值.
實務上我們可以用一個 calibration set 用 $\alpha := \mathbb{E}_t[\beta_t]=\sum_t\sum_x\min(p_t(x),q_t(x))$ 估計出來
而 $c$ 則跑 $M_p,M_q$ 的 inference 測出來.
接著選擇 approx. and target models 有 $\alpha>c$ 的配對, 最後 $\gamma$ 則求解本篇公式 (1) 找出最佳值來.
給定 $\alpha,c$ 對式 (1) 做數值最佳化找出最佳 $\gamma$, 結果如下: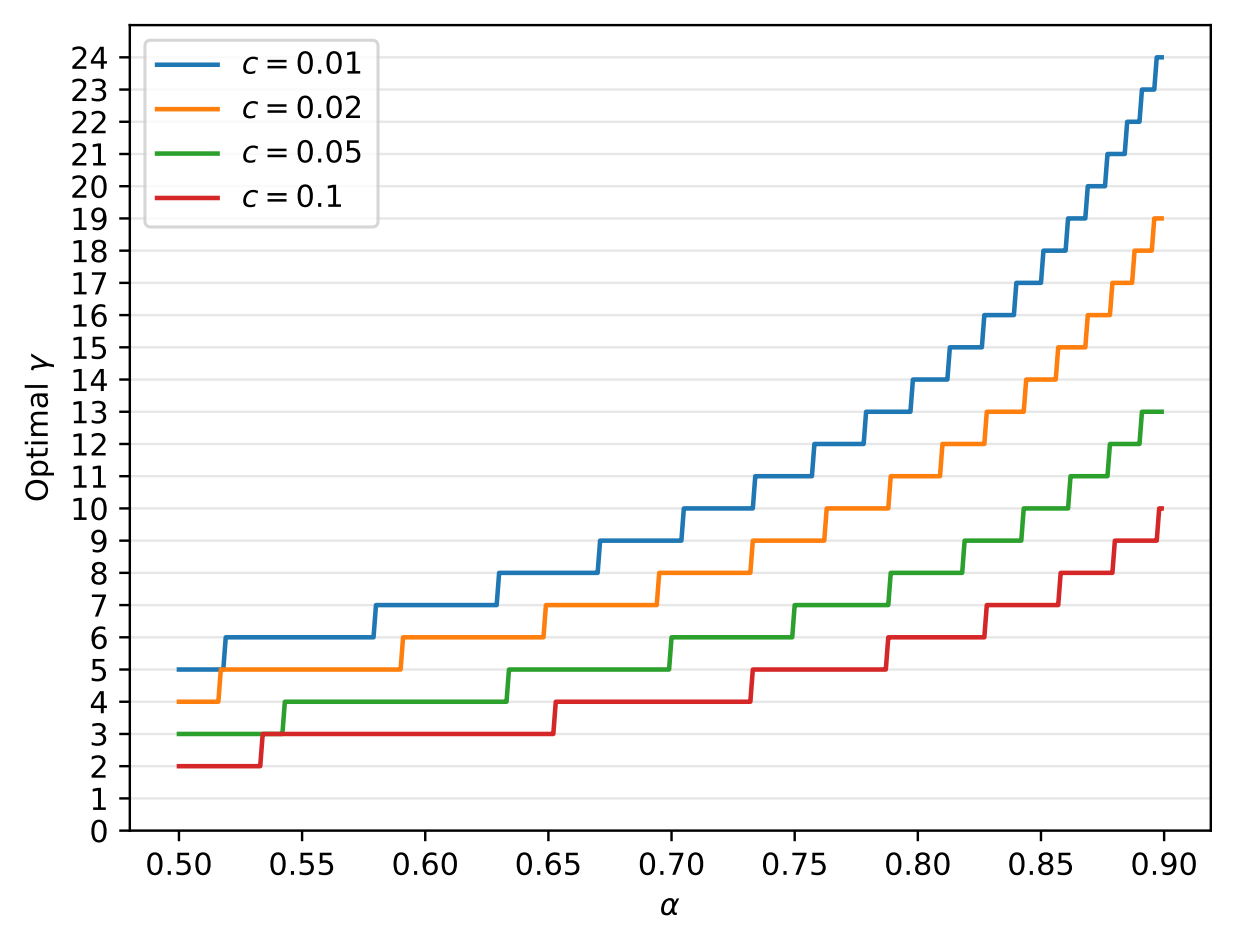 最後 walltime improvement 理論值式 (1) 和實際上量測出來的值有沒有差很多? 作者做了個比較
最後 walltime improvement 理論值式 (1) 和實際上量測出來的值有沒有差很多? 作者做了個比較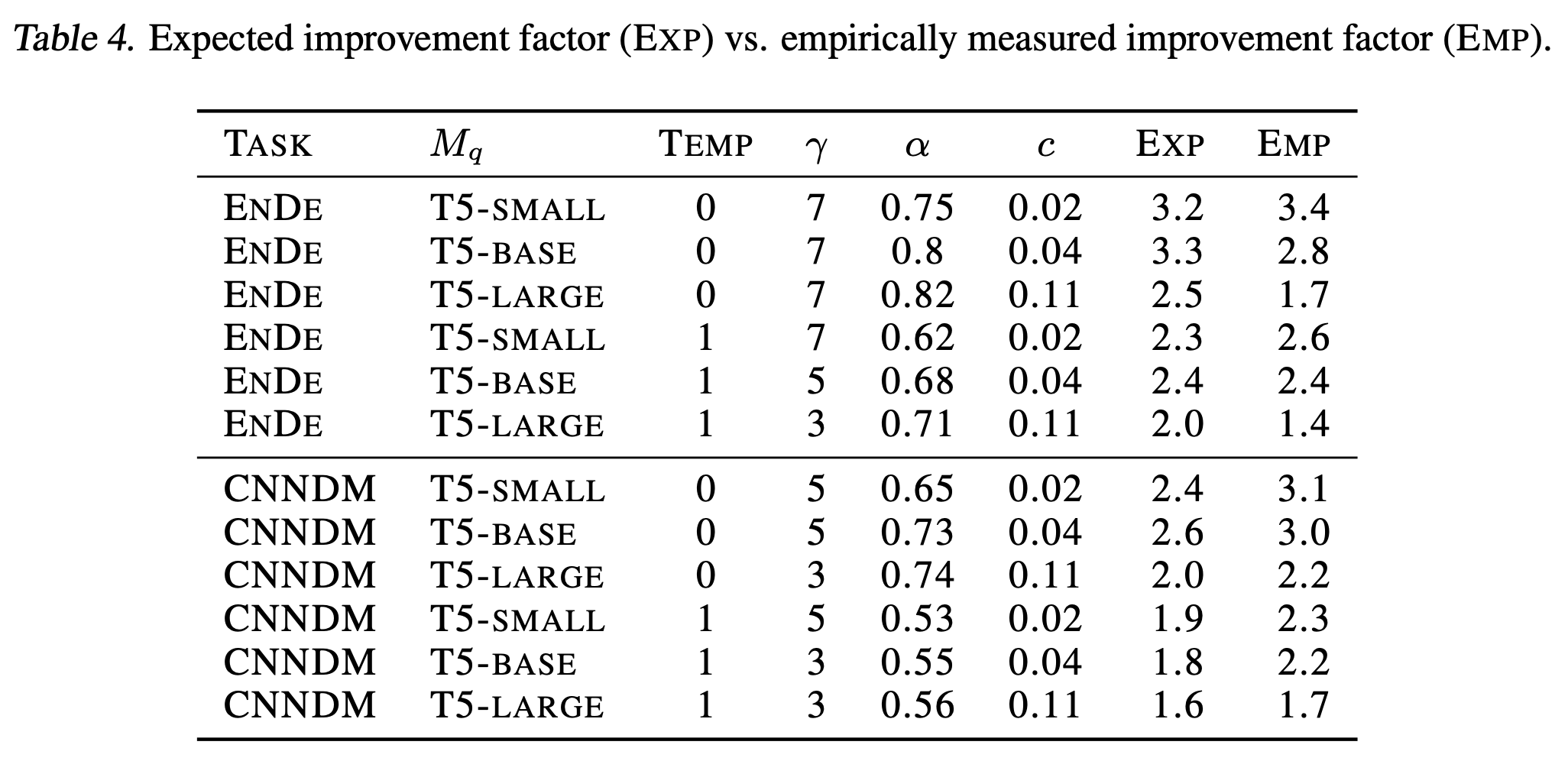
EXP 是式(1) 計算的, EMP 是實際量測的, 雖然沒很準確, 但也算是正相關
B. 運算量的分析
將上一篇的公式 (10):
$$\mathbb{E}[\#\text{generated tokens}]=\frac{1-\alpha^{\gamma+1}}{1-\alpha}$$ 代入上一篇的公式 (6)
$$\#\text{OPs Increasing Ratio}= \frac{\hat{c}\gamma+\gamma+1}{\mathbb{E}(\#\text{generated tokens})}$$ 我們得到
$$\begin{align}
\#\text{OPs Increasing Ratio}=\frac{(\hat{c}\gamma+\gamma+1)(1-\alpha)}{1-\alpha^{\gamma+1}}
\end{align}$$ 我們一樣把圖畫出來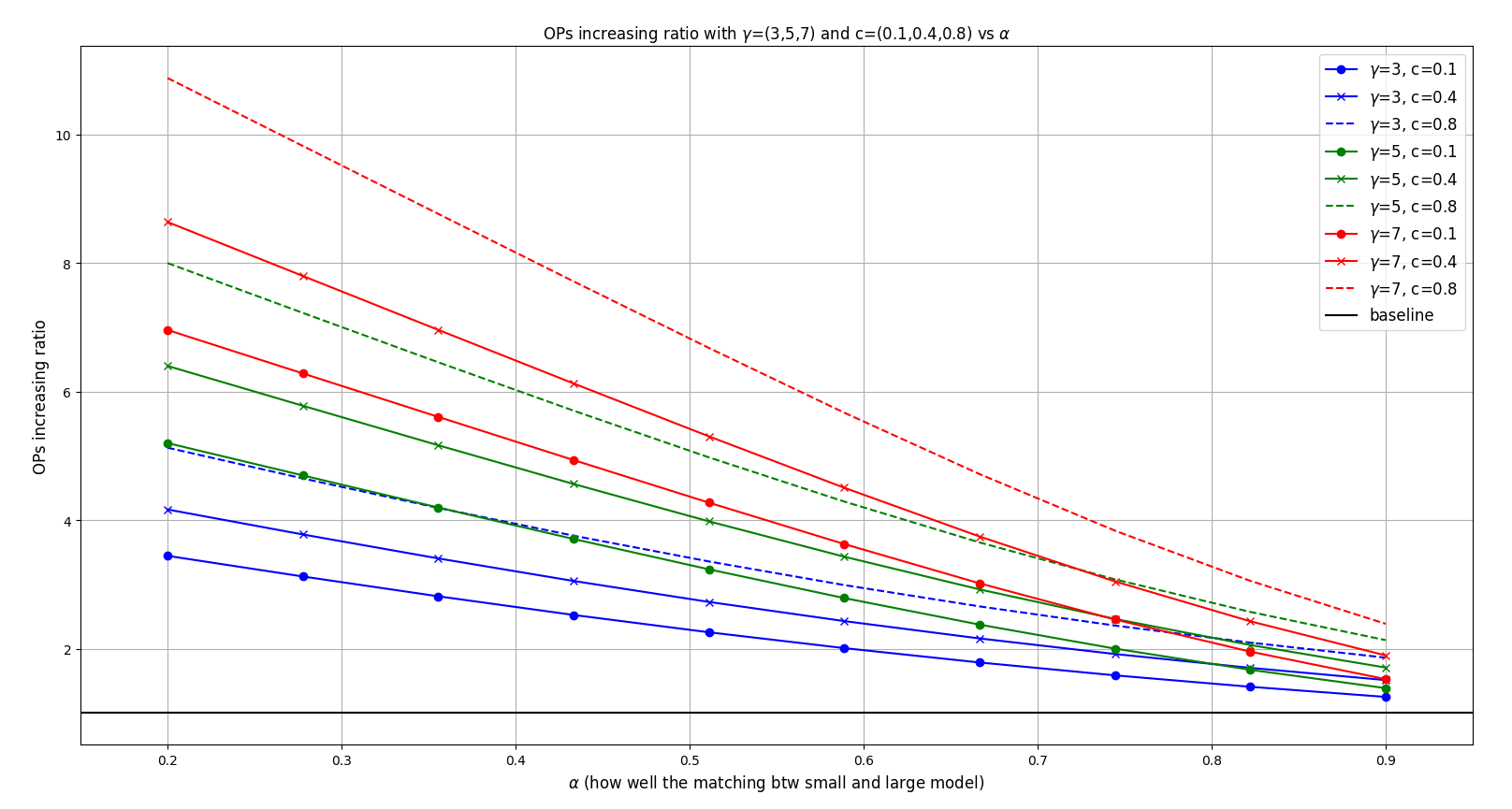
觀察到幾點 (除了最後第4點的結論, 其他聽起來都像”每60秒就會有1分鐘過去”一樣地廢話):
1. 如果 $\alpha$ 愈小 (大小模型愈不匹配), 則運算量增加愈多
2. $c$ 愈小 (小模型速度愈快) 則運算量增加的 overhead 愈少
3. $\gamma$ 愈大則花愈多運算量
4. 比較需要注意的是, 不管怎樣都會花額外的計算量, 因為都比 baseline 高
是不是有點反直覺, 上面說可以加速, 但又說運算量會比較多. 其實原因就是 target model 可以並行算
C. Memory Bandwidth 的分析
這個理論分析比較單純, 由於 speculative 一個 run 的時候 target model 只會呼叫一次, 對比原本每產生一個 token 都要呼叫一次 target model
Loading 參數和 kv cache 這些 memory bandwidth 的次數就少非常多, 少的比例次數基本上就是 $\mathbb{E}(\# \text{generated tokens})$ 上一篇的公式 (10) 的比例:
$$\mathbb{E}[\#\text{generated tokens}]=\frac{1-\alpha^{\gamma+1}}{1-\alpha}$$
D. Performance 能維持住嗎?
回到一開始就破題說 performance 能維持住這件事. 如果不能維持, 上面所有分析都在做白工.
論文的 Appendix A.1. 證明寫的很明白, 基本重複一遍而已
回顧 $\beta$ 表示時間 $t$ 的 accept probability (忽略下標 $t$)
$$\beta = \sum_x\min(p(x),q(x))$$ Modified distribution:
$$p'(x)=norm(\max(0,p(x)-q(x))) \\
=\frac{p(x)-\min(q(x),p(x))}{\sum_{x'}(p(x')-\min(q(x'),p(x')))} \\
= \frac{p(x)-\min(q(x),p(x))}{\sum_{x'}p(x')-\sum_{x'}\min(q(x'),p(x'))} \\
= \frac{p(x)-\min(q(x),p(x))}{1-\beta}$$ 考慮 speculative decoding 最終採樣出 token $x’$ 的機率為:
$$P(x=x')=P(\text{guess accept},x=x') + P(\text{guess reject},x=x')$$ 其中
$$P(\text{guess accept},x=x')=q(x')\min\left(1, \frac{p(x')}{q(x')}\right)=\min(q(x'),p(x'))$$ 注意到 speculative decoding 接受的情況是:
1. 當 $p(x') \geq q(x')$ 時會 accept
2. 否則有 $p(x')/q(x')$ 的機率 accept
這樣寫起來就是 $\min(1, p(x')/q(x'))$ 的機率. 然後 accept 的話, token 是從 approx. model 採樣的, 因此是 $q(x’)$.
另外
$$P(\text{guess reject},x=x')=(1-\beta)p'(x')=p(x')-\min(q(x'),p(x'))$$ Reject 的話要從 modified distribution $p’(x)$ 去採樣.
所以合在一起我們得到 $P(x=x’)=p(x’)$
References
- Google: Fast Inference from Transformers via Speculative Decoding [arvix]
- DeepMind: Accelerating Large Language Model Decoding with Speculative Sampling [arxiv]
- Speculative Decoding 詳讀 (上)