在這篇之前的 NAS (Neural Architecture Search) 主流方法為 evolution or RL 在 discrete space 上搜尋, 雖然可以得到當時最佳的結果, 但搜索的 cost 很高.
這篇提出 DARTS (Differentiable ARchiTecture Search) 將 NAS 變成 continuous relaxation 的問題後, 就能套用 gradient-based optimize 方法來做 NAS. 因此比傳統方法快上一個 order. 雖然 gradient-based NAS 在這篇文章之前就有, 但是之前的方法沒辦法像 DARTS 一樣能套在各種不同的 architecture 上, 簡單講就是不夠 generalized.
核心想法是, 如果一個 layer 能包含多個 OPs (operations), 然後有個方法能找出最佳的 OP 應該是那些, 對每一層 layers 都這樣找我們就完成 NAS 了.
圖片來源, 或參考這個 Youtube 解說, 很清楚易懂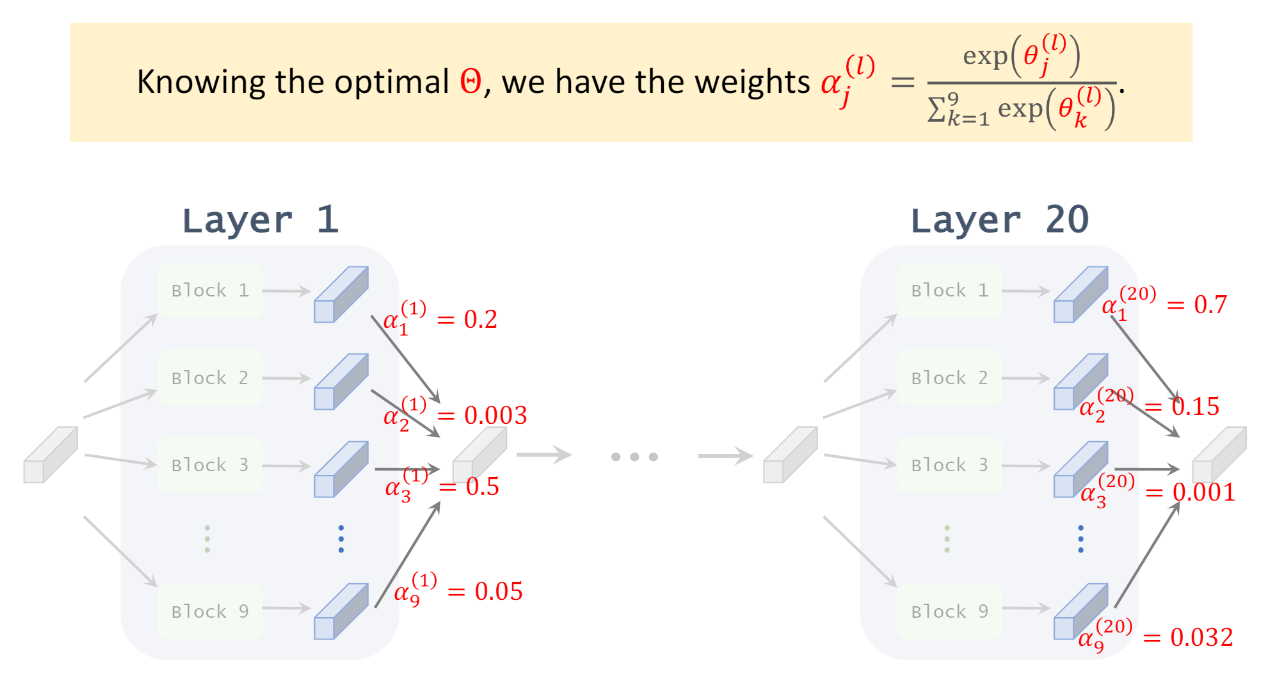 不過關鍵是怎麼找? 這樣聽起來似乎需要為每個 OPs 都配上對應可訓練的權重, 最後選擇權重大的那些 OPs? 以及怎麼訓練這些架構權重?
不過關鍵是怎麼找? 這樣聽起來似乎需要為每個 OPs 都配上對應可訓練的權重, 最後選擇權重大的那些 OPs? 以及怎麼訓練這些架構權重?
或這麼類比: 直接訓練一個很大的 super network, 根據 OP 對應的架構權重來選擇哪些 OPs 要留下來, 大概類似 model pruning 的想法
怎麼結合多個 OP? 每個 OP 都訓練個權重? 以及怎麼選擇哪個 OP?
NN 的 forward inference (computational graph) 是個 DAG (Directional Acyclic Graph), 我們假設依循這個 DAG 可得到 inference 的 tensor sequences $\{x^{(1)}, x^{(2)}, ..., x^{(n)}\}$ 其中 $x^{(1)}$ 是 NN 的 input tensor, $x^{(n)}$ 是 output tensor
因此要得到 tensor $x^{(j)}$ 可以這麼做:
$$\begin{align} x^{(j)}=\sum_{i<j}o^{(i,j)}\left(x^{(i)}\right) \end{align}$$ 把小於第 $j$ 個 tensor 的所有 tensor 都執行完後即可得到. 其中 $o^{(i,j)}$ 表示 tensor $i$ 與 $j$ 的 operation.這個 operation 原本都是人為手工定義好的, 例如 $o^{(2, 4)}=\text{Conv2d}$, $o^{(4,9)}=\text{maxpool}$, …
DARTS 將人為定義的 operation 變成可用 gradient 去學出來.
定義 $\mathcal{O}$ 是所有可能的 operation 的集合, e.g.
$$\mathcal{O}=\{\text{conv2d, fc, rnn, maxpool, ..., } {\color{orange}{\text{zero}}}\}$$
對於 tensor $i$ and tensor $j$ 的 operation 吃 input $x$, 則 output 定義為:
$$\begin{align}
\bar o^{(i,j)}(x)=\sum_{o\in\mathcal{O}}\frac
{\exp\left(\alpha_o^{(i,j)}\right)}
{\sum_{o'\in\mathcal{O}}\exp\left(\alpha_{o'}^{(i,j)}\right)}o(x)
\end{align}$$ 定義看起來好像很複雜, 我們舉個 toy example 應該就會清楚很多.
令 $\mathcal{O}=\{\text{conv2d},\text{maxpool}, \text{zero}\}$, 只有 3 種 operations.
對於 edge $(i,j)$ 來說假設這 3 個 op 的機率分別為 $\{0.2, 0.5, 0.3\}$ 則:
$$\begin{align} \bar{o}^{(i,j)}(x)=0.2\cdot\text{conv2d}(x) + 0.5\cdot\text{maxpool}(x) + 0.3\cdot\text{zero(x)} \end{align}$$ 因此 output $x^{(j)}$ 就是:
$$\begin{align}
x^{(j)}=\sum_{i<j}\bar{o}^{(i,j)}\left( x^{(i)}\right)
\end{align}$$ 可以看出來每一個 $(i,j)$ 都有一個 operations 的機率分佈 $\{p_o^{(i,j)}\}_{o\in\mathcal{O}}$.
其中 $\sum_{o\in\mathcal{O}}p_o^{(i,j)}=1$, 或以 logits 來看就是 $\{\alpha_o^{(i,j)}\}_{o\in\mathcal{O}}$. 而這個 $\alpha_o^{(i,j)}$ 就是會跟著 NN 的 weights 一起訓練得到.
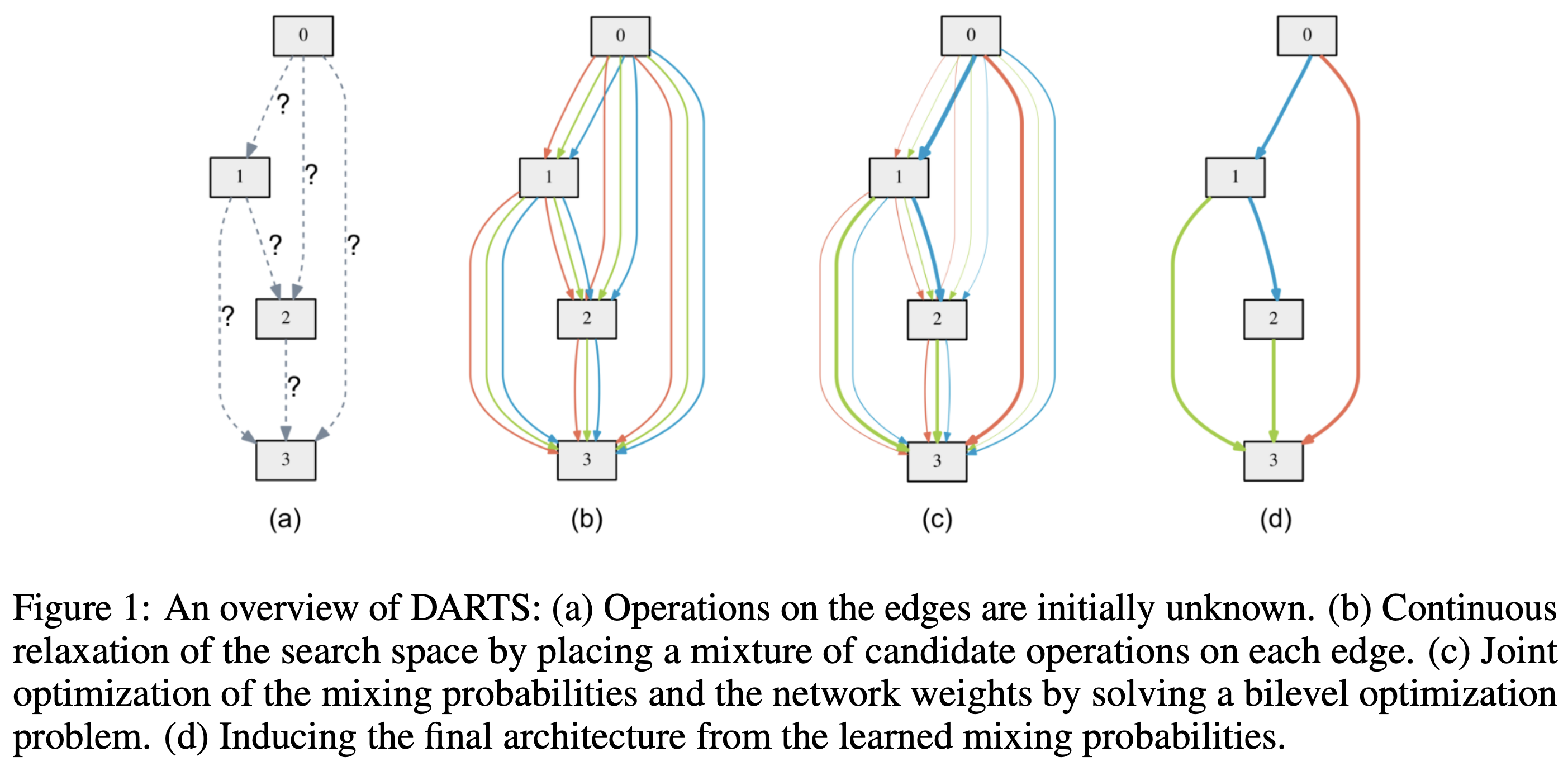 論文稱 $\{\alpha_o^{(i,j)}\}_{o\in\mathcal{O},i,j}$ 為 mixing probabilities, 訓練完成後可以選擇機率最大 (or topk) 的 operations 當作最後的 network 架構.
論文稱 $\{\alpha_o^{(i,j)}\}_{o\in\mathcal{O},i,j}$ 為 mixing probabilities, 訓練完成後可以選擇機率最大 (or topk) 的 operations 當作最後的 network 架構.
由於我們有 include $\color{orange}{\text{zero}}$ 這個 operation, 所以如果他的機率最高, 其實就表示 edge $(i,j)$ 相當於不存在, i.e. tensor $i$ 與 $j$ 不相連. 但其實作者有提到 zero 的權重估計應該會有點問題, 因為不管 zero 的權重大小都不影響最終辨識結果, 不確定這後面有沒有改善方式. 倒是如果有 identity OP 則變成 skip layer 的效果, 這可能會有一些問題出現, Fair DARTS 提出這個問題並嘗試解決 (待讀)
目標函式和搜索參數 $\alpha$ 的求導
Objective function:
$$\begin{align}
\min_{\alpha}\mathcal{L}_{\color{red}{val}}\left(w^*(\alpha), \alpha\right) \\
\text{s.t.}\quad w^*(\alpha)=\arg\ min_w\mathcal{L}_{\color{red}{train}}(w,\alpha)
\end{align}$$ 注意到 $\alpha$ 的選擇是在 validation set 上, 而 NN 的 $w$ 則是在 training set 上訓練. 作用就是用 training loss 訓練模型參數,用 validation loss 找模型結構.
這樣的問題是 bilevel optimization problem (Anandalingam & Friesz, 1992; Colson et al., 2007)
$\alpha$ 是 upper-level variable, 而 $w$ 是 lower-level variable.
💡如果 $\alpha$ 的選擇是在 training set 上, 則不需這麼複雜, 直接一起跟 $w$ jointly training 就好, 這樣是不是更簡單??
$$\min_{\alpha,w}\mathcal{L}_{train}(w,\alpha)$$ 論文做了這樣的實驗跟 bi-level optimization 對比, 相同參數量和訓練資料 (train+validation sets) 跑四次 random seeds 結果, CIFAR10 得到的 test error rate 為 3.56 ± 0.10%, 而 bi-level optimization 方法最好為 2.76 ± 0.09%, 作者推測是 architecture $\alpha$ 跟著一起訓練會 overfit (因為在 bi-level 方法 $\alpha$ 是在 validation set 上) 因此泛化能力變差.
直接優化是很難的, 所以論文提出以下的近似:
$$\begin{align}
\nabla_\alpha\mathcal{L}_{val}(w^*(\alpha),\alpha) \\
\approx\nabla_\alpha\mathcal{L}_{val}\left(w-\xi\nabla_w\mathcal{L}_{train}(w,\alpha),\alpha\right)
\end{align}$$ 原本要計算 $w^*(\alpha)$ 需要解 inner loop (6), 作者直接用一次 training step 來當作近似解 (8)
對 (8) 使用 multivariable chain rule [ref] 計算 gradient 得到:
$$\begin{align}
\nabla_\alpha\mathcal{L}_{val}(w',\alpha)-\xi{\color{orange}{\nabla_{\alpha,w}^2\mathcal{L}_{train}(w,\alpha)\cdot\nabla_{w'}\mathcal{L}_{val}(w',\alpha)}}
\end{align}$$(寫清楚一點: $\nabla_{w'}\mathcal{L}_{val}(w',\alpha)$ 是 $\left.\nabla_w\mathcal{L}_{val}(w,\alpha)\right|_{w=w'}$ 的簡寫)
其中 $w'=w-\xi\nabla_w\mathcal{L}_{train}(w,\alpha)$. 當 $\xi=0$, 稱為 first order 解, 否則 second order.
橘色這項因為二階微分的計算代價很高, 所以使用數值逼近的方式計算. (這個技巧請參考 Appendix)
令 $w^{\pm}=w\pm\epsilon\nabla_{w'}\mathcal{L}_{val}(w',\alpha)$, 則
$$\begin{align} \nabla_{\alpha,w}^2\mathcal{L}_{train}(w,\alpha)\cdot\nabla_{w'}\mathcal{L}_{val}(w',\alpha) \approx \frac{ \nabla_\alpha\mathcal{L}_{train}(w^+,\alpha) - \nabla_\alpha\mathcal{L}_{train}(w^-,\alpha) } {2\epsilon} \end{align}$$(10) 的 R.H.S. 只要 $\lim_{\epsilon\rightarrow0}$ 的話, 就是對 $w$ 在 $\nabla_{w'}\mathcal{L}_{val}(w',\alpha)$ 方向上的微分, 所以是 directional derivatives.
L.H.S. 請參考 Directional derivatives wiki 說明: $\nabla_v f(x)=\nabla f(x)\cdot v$ provided by $f$ is differentialble at $x$.
另外作者補充說一般 $\epsilon=0.01/\|\nabla_{w'}\mathcal{L}_{val}(w',\alpha)\|_2$ 在他們的實驗都可以.
所以總結 $\alpha$ 的 gradient 為:
$$\begin{align} \nabla_\alpha\mathcal{L}_{val}(w^*(\alpha),\alpha) \approx \nabla_\alpha\mathcal{L}_{val}(w',\alpha)-\xi\frac{ \nabla_\alpha\mathcal{L}_{train}(w^+,\alpha) - \nabla_\alpha\mathcal{L}_{train}(w^-,\alpha) } {2\epsilon} \end{align}$$其中 $w'=w-\xi\nabla_w\mathcal{L}_{train}(w,\alpha)$ 相當於做一次 $w$ 的 gradient update, 然後 $w^{\pm}=w\pm\epsilon\nabla_{w'}\mathcal{L}_{val}(w',\alpha)$.
對照 PyTorch 的求導 Codes
那實際上怎麼 implement 的? 讓我們解析一下這段 official codes row 2
row 2 _compute_unrolled_model() 計算了 unrolled_model ($w’$), 其中 eta 指 (8) 的 $\xi$.
有了 $w’$ 才能計算 $\mathcal{L}_{val}(w',\alpha)$: unrolled_loss = unrolled_model._loss(input_valid, target_valid)
注意到 $w’$ 和 $\alpha$ 都是 torch 的 parameters, 所以接著 unrolled_loss.backward()
這行 code 我們可以同時得到 $\nabla_{w'}\mathcal{L}_{val}(w',\alpha)$(vector) 和 $\nabla_\alpha\mathcal{L}_{val}(w',\alpha)$(dalpha)
接著 self._hessian_vector_product() 就可以計算 (10)了 (因為有了 vector 我們就可以計算 $w^{\pm}$):
$$\begin{align}
\frac{
\nabla_\alpha\mathcal{L}_{train}(w^+,\alpha) - \nabla_\alpha\mathcal{L}_{train}(w^-,\alpha)
}
{2\epsilon}
\end{align}$$計算出來的值稱 implicit_grads
最後結合 dalpha 就可以得到最終的 $\alpha$ gradient (11) 了, 這步: g.data.sub_(eta, ig.data)
整體 algorithm 如下:
一些總結 and References
DARTS 開啟了廣泛使用 gradient-based NAS 的方法. 但也還有些可以改進的地方, 如:
- Architecture 參數 $\alpha$ 或許可以讓他更傾向 one-hot 的結果, 因為如果每個 OPs 學出來都差不多重要, 那最後只保留 top-1 的 OP 效果就不大:
論文說可以使用 softmax annealing 方式, 漸漸變 one-hot, 或我猜可使用 Stochastic NAS (SNAS) - 記憶體的使用量仍然很大:
這是因為每個 candidate OPs 其實都需要在 computational graph 中保留, 需要做 backward gradients. 因此通常先在 proxy task 上 search, 譬如只用一部分訓練資料或只找部分 NN 的 OPs 等. 然後再把結果轉移到完整資料或大的 NN 上. ProxylessNAS 改進了這一缺點. - 搜尋或許可以加入 target 平台的考量, 譬如 latency, MCPS 限制, memory 限制等 … ProxylessNAS 考慮了這些
- Skip layer 可能會有些問題, FairDARTS 嘗試改進這點
Related repositories:
- 原始的 DARTS codes 只支援使用
PyTorch == 0.3.1, 硬在 PyTorch 1.12.1 跑得起來, 反正就是遇到 error 就修, 大部分是 API 的不同 - https://github.com/khanrc/pt.darts: 從 official 改的, 有些注釋和改動並且好閱讀, 同時支援
PyTorch >= 0.4.1and multi-GPU - FairDARTS
- MicroSoft [archai]: bilevel_optimizer.py
Appendix 微分數值逼近技巧
首先我們知道
$$f(x+h)=f(x)+f'(x)h+\frac{1}{2}f''(x)h^2+\frac{1}{3!}f'''(x)h^3+O(h^4)$$所以
$$f'(x)\approx\frac{f(x+h)-f(x)}{h}=f'(x)+O(h)$$如果我們利用
$$f(x-h)=f(x)-f'(x)h+\frac{1}{2}f''(x)h^2-\frac{1}{3!}f'''(x)h^3+O(h^4)$$則可以將 $f’(x)$ 的數值逼近下降一個 order:
$$f'(x)\approx\frac{f(x+h)-f(x-h)}{2h}=f'(x)+O(h^2)$$利用這種做法, 我們可以將 (9) 的這項 $\nabla_{\alpha,w}^2\mathcal{L}_{train}(w,\alpha)\cdot\nabla_{w'}\mathcal{L}_{val}(w',\alpha)$ 用數值逼近做出來: