Maximal Log-likelihood 是很多模型訓練時目標函式. 在訓練時除了 observed data $x$ (蒐集到的 training data) 還會有無法觀測的 hidden variable $z$ (例如 VAE 中 encoder 的結果).
如何在有隱變量情況下做 MLE, Evidence Lower BOund (ELBO) 就是關鍵. 一般來說, 因為 ELBO 是 MLE 目標函式的 lower bound, 所以藉由最大化 ELBO 來盡可能最大化 likelihood. 另外這個過程也可以用來找出逼近後驗概率 $p(z|x)$ 的函式. 本文記錄了 ELBO 在 Variational Inference (VI), Expectation Maximization (EM) algorithm, 以及 Diffusion Model 三種設定下的不同用法.
數學比較多, 開始吧!
開頭先賞一頓數學操作吃粗飽一下
Let $p,q$ 都是 distributions, 則下面數學式子成立
$$\log p(x)= KL(q(z)\|p(z|x))+ {\color{orange}{ \mathbb{E}_{z\sim q}\left[\log \frac{p(x,z)}{q(z)}\right]} }\\ =KL(q(z)\|p(z|x))+{\color{orange}{ \mathbb{E}_{z\sim q}\left[\log p(x,z) - \log q(z)\right]} } \\ =KL(q(z)\|p(z|x))+\color{orange}{\mathcal{L}(q)}$$ 因為 $KL(\cdot)\geq0$ 所以 $\mathcal{L(q)}\leq\log p(x)$
基本上 $p,q$ 只要是 distribution 上面式子就成立
如果把 $p(x)$ 用 $\theta$ 參數化 (例如用 NN 來 modeling 則 $\theta$ 為 NN 的參數), 則
$$\log p(x|{\color{red}\theta})=KL(q(z)\|p(z|x,{\color{red}\theta}))+
\mathbb{E}_{z\sim q}\left[\log p(x,z|{\color{red}\theta}) - \log q(z)\right] \\
=KL(q(z)\|p(z|x,{\color{red}\theta}))+\mathcal{L}(q,{\color{red}\theta})$$ 上面這一頓數學操作下來, 正常人應該也看不懂要怎麼用…
上面突然冒出來的 $q(z)$ 分佈我們稱為 auxiliary function, 沒有特別指明是什麼樣的分佈, 就因為多出來的這個彈性, 神奇的用法就出來了
反正就是大有用處對了 XD, 以下紀錄目前學到的三種用法:
1. Variational Inference (VI) 用法: 真實的後驗概率 $p(z|x)$ 未知, 想在定義好的一個 distribution space 裡面找到一個 distribution $q(z)$ 最接近 $p(z|x)$.
2. Expectation Maximization (EM) algorithm 用法: 在有 hidden variable $z$ 情況下做 MLE (maximal likelihood estimation), 即找出 $\theta$ 最大化 marginal log likelihood, $\arg\max_\theta \log p(x|\theta)$. 注意到 Variational Auto-Encoder (VAE) 也是這麼用的
3. Diffusion Model 用法: 如同 EM 用法一樣做 MLE, 唯一不同的是, 此時我們知道真實的後驗概率分布: “Markov chain 定義下, 真實後驗概率 $p(x_t|x_0)$ 有 closed form solution”. 所以不用 optimize $q$ 分布, 而是把 $q$ 直接設定成 $p(x_t|x_0)$ 的真實分布. 然後一樣求解 MLE 找 $\arg\max_\theta \log p(x|\theta)$
補充一下設定好了. $x$ 通常是我們觀測到的資料, $p(x)$ 就是觀測資料的分佈, 寫 $p(x|\theta)$ 就是我們用模型參數 $\theta$ 找的資料分佈, 通常藉由 maximal likelihood estimation (MLE) 最大化 $p(x|\theta)$ 的方法找到 $\theta$. $z$ 通常表示 latent (hidden) variable. 而後驗概率 posterior probability $p(z|x)$ 可以這麼簡單理解一下, 假設 latent variable $z=\{\text{cat},\text{dog}\}$ 只有兩個值, 則 $p(z=\text{cat}|x)$ 表示觀測到某張影像 $x$ 是貓的機率.
我知道還是看不懂, 反正就記住這個 ELBO (Evidence Lower BOund) 不等式:
$$\begin{align}
{\color{orange}{\log p(x)}} = KL(q(z)\|p(z|x))+
\mathcal{L}(q){\color{orange}{\geq\mathcal{L}(q)}} \\
\mathcal{L(q)}:=\mathbb{E}_{z\sim q}\left[\log p(x,z) - \log q(z)\right]
\end{align}$$ 下面比較詳細一些來紀錄上面三種用法, 也恭喜有耐心看到這的讀者.
Variational Inference (VI) 用法
在 Variational Inference (VI) 設定中 $p$ 是真實的 distribution, 我們希望找出真實的後驗概率分布 $p(z|x)$, 因此定義一個 distribution space $\mathcal{Q}$, where $q\in\mathcal{Q}$, 使得 $KL(q(z)\|p(z|x))$ 愈小愈好, i.e.
$$q^\ast=\arg\min_{q\in\mathcal{Q}} KL(q(z)\|p(z|x))$$ 當 $KL=0$ 的時候 $q(z)^\ast=p(z|x)$, 我們就歡天喜地的找到解了, $q^\ast$.
但就是因為我們不知道真實的後驗概率分布 $p(z|x)$, 上式的 $KL$ loss function 也根本無法計算, 怎麼辦呢?
觀察式 (1) 注意到 $\log p(x)$ 跟我們要找的 $q(z)$ 無關, 也就造成了 $\log p(x)$ 是固定的. 由於 $KL\geq0$, 讓 $KL$ 愈小愈好等同於讓 $\mathcal{L}(q)$ 愈大愈好. 因此藉由最大化 $\mathcal{L}(q)$ 來迫使 $q(z)$ 接近 $p(z|x)$.
$$q^\ast=\arg\max_{q\in\mathcal{Q}}\mathcal{L}(q)$$ 這樣我們就找到一個後驗概率 $p(z|x)$ 的近似替代解了, i.e. $q(z)$
從 (2) 看出最大化 $\mathcal{L}(q)$ 會需要計算 $p(x,z)$, 但通常這項都比較好計算所以不用擔心 (參考GMM 的設定)
Expectation Maximization (EM) Algorithm 用法
在 EM 的設定上, 我們則是希望找到一組參數 $\theta^\ast$ 可以讓 marginal log likelihood $\log p(x|\theta)$ 最大:
$$\theta^\ast=\arg\max_\theta \log p(x|\theta)$$ 此時要求的變數不是 $q$ 而是 $\theta$
$$\log p(x|{\color{red}\theta})=KL(q(z)\|p(z|x,{\color{red}\theta}))+
\mathbb{E}_{z\sim q}\left[\log p(x,z|{\color{red}\theta}) - \log q(z)\right] \\
=KL(q(z)\|p(z|x,{\color{red}\theta}))+\mathcal{L}(q,{\color{red}\theta})$$ 這時候 $\log p(x|\theta)$ 不再是固定的 (VI 是), 而是我們希望愈大愈好. 而我們知道 $\mathcal{L}(q,\theta)$ 是它的 lower bound 這點不變, 因此如果 lower bound 愈大, 則我們的 $\log p(x|\theta)$ 就當然可能愈大.
所以 EM algorithm 一樣最大化 ELBO $\mathcal{L}(q,\theta)$ 來達到最大化 marginal log likelihood
$$q^\ast,\theta^\ast=\arg\max_{q,\theta}\mathcal{L}(q,\theta) \\
\mathcal{L}(q,\theta):=\mathbb{E}_{z\sim q}\left[\log p(x,z|\theta) - \log q(z)\right]$$ 所以 EM algorithm 的用法只是比 VI 的用法多優化了 $\theta$ 來做 MLE (maximal likelihood estimation), i.e. 最大化 log likelihood $\log p(x|\theta)$. 相當於有 hidden variable $z$ 情況下的 MLE
這個也是 VAE (Variational Auto-Encoder) 的用法
更多請參考以前的筆記 [Appendix: EM 跟 VI 很像阿]
Diffusion Model 用法
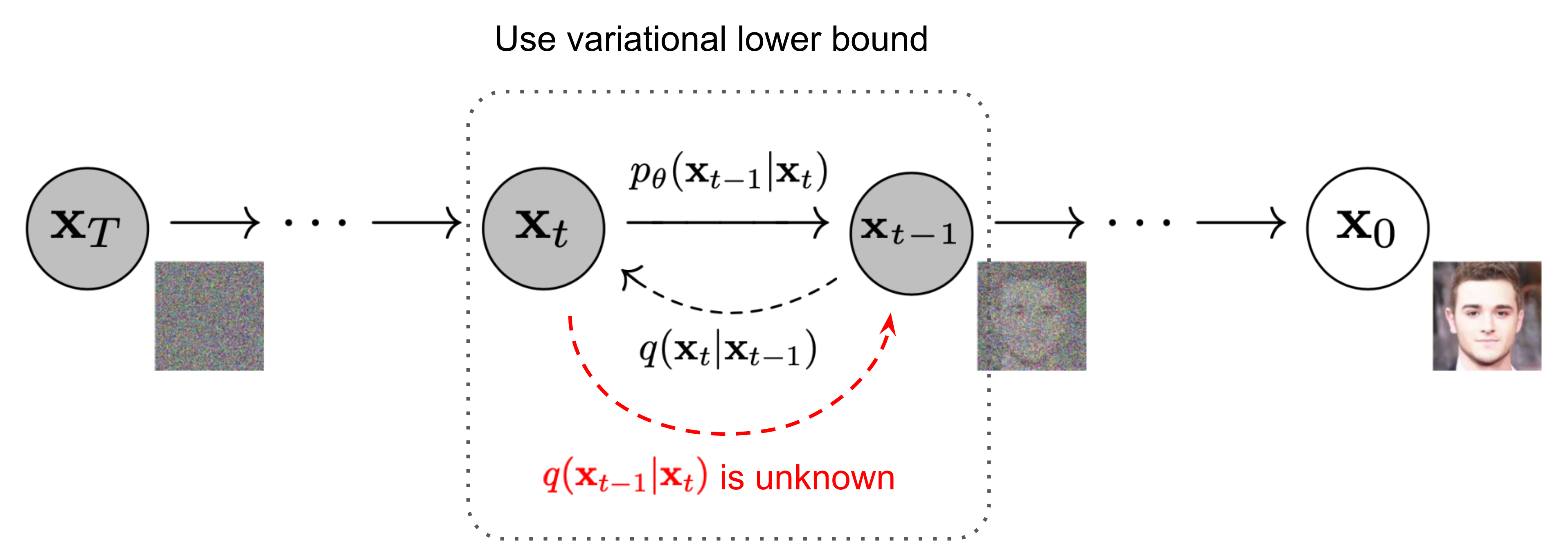
先說一下 diffusion model 的設定 (from Lil’Log, 但把原圖的 $q(\cdot)$ 變成 $p(\cdot)$ 為了符合本文的符號定義, 因為本文 $q$ 是用做 auxiliary function)
- $x_0$ 表示 observation data (e.g. 乾淨影像)
- $x_T$ 表示加噪到最後的 Gaussian noise 影像 (分佈直接就是 standard Gaussian 與 data 分佈無關)
透過 diffusion model 定義的 forward process 來加噪:
$$\begin{align}
p(\mathbf{x}_t \vert \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t\mathbf{I})
\end{align}$$ 和使用 Markov chain 的設定, $p(x_{1:T}|x_0)$ 是可以直接寫出來的:
$$\begin{align}
p(\mathbf{x}_{1:T} \vert \mathbf{x}_0) = \prod^T_{t=1} p(\mathbf{x}_t \vert \mathbf{x}_{t-1})
\end{align}$$ Diffusion model 一樣做 MLE (maximal likelihood estimation), 要找出最佳的 $\theta^\ast$ 使得 $\log p(x|\theta^\ast)$ 最大. 一樣觀察下式
$$\log p(x|{\color{red}\theta})=KL(q(z)\|p(z|x,{\color{red}\theta}))+
\mathbb{E}_{z\sim q}\left[\log p(x,z|{\color{red}\theta}) - \log q(z)\right] \\
=KL(q(z)\|p(z|x,{\color{red}\theta}))+\mathcal{L}(q,{\color{red}\theta})$$ 此時設定 $x_0$ 對應到 $x$ 是 observed data (e.g. 乾淨影像), 而 $x_{1:T}$ 是我們看不到的 hidden variable $z$ (e.g. 加噪過程的影像), 則我們知道真實的 posterior $p(z|x)$ 由式 (3, 4) 是已知的.
因為我們的問題不是要找 $q$ 去逼近 $p(z|x)$, 直接把 $q$ 設定成已知的 $p(z|x)$ 即可, i.e.:
$$\begin{align}
q(z):=p(z|x)
\end{align}$$ 然後一樣最大化 ELBO $\mathcal{L}(\theta)$ (由於 $q$ 是已知固定數學式子不是要找的參數, 所以從 $\mathcal{L}(\theta,q)$ 去掉) 來找出最佳的 $\theta^*$ 使得 marginal log likelihood $\log p(x|\theta)$ 也變大
$$\theta^\ast=\arg\max_\theta\mathcal{L}(\theta)$$ 從原本的 ELBO 出發 (式 (1, 2)) 改寫一下:
$$\begin{align}
\log p(x|\theta)\geq\mathcal{L}(\theta):=\mathbb{E}_{z\sim q(z)}\left[\log p(x,z|\theta) - \log q(z)\right] \\
\Longrightarrow \mathbb{E}_{x\sim p(x)}\log p(x|\theta) \geq \mathbb{E}_{x\sim p(x),z\sim {\color{orange}{q(z)}}}\left[\log p(x,z|\theta) - \log {\color{orange}{q(z)}}\right] \\
\Longrightarrow \mathbb{E}_{x\sim p(x)}\log p(x|\theta) \geq \mathbb{E}_{x\sim p(x),z\sim {\color{orange}{p(z|x)}}}\left[\log p(x,z|\theta) - \log {\color{orange}{p(z|x)}}\right]
\end{align}$$ 式 (7) 到 (8) 是因為 (5) 我們定義這樣的關係
我們來對應一下 Diffusion model 的 loss (式 (9) 參考自 [What are Diffusion Models?]) VLB (Variational Lower Bound):
$$\begin{align}
L_{VLB}=\mathbb{E}_{p(x_{0:T})}\left[
\log\frac{p(x_{1:T}|x_0)}{p(x_{0:T}|\theta)}
\right]
\geq -\mathbb{E}_{p(x_0)}\log p(x_0|\theta) \\
\Longrightarrow
\mathbb{E}_{p(x_0)}\log p(x_0|\theta) \geq \mathbb{E}_{p(x_{0:T})}\left[
\log{p(x_{0:T}|\theta)-\log{p(x_{1:T}|x_0)}}
\right] \\
\end{align}$$ 對照一下 (8) 和 (10) 可以知道:
- observation variable 為 $x_0$ (原始乾淨影像, 我們原本用 $x$ 表示)
- hidden variable 為 $x_{1:T}=\{x_1,x_2,...,x_T\}$ (中間加噪的過程影像, 我們原本用 $z$ 表示)
然後回頭看 (4) 和 (5) 也能對的上
把握這個概念再去看 Diffusion model 的 loss 推導或許會更清楚 loss 在優化什麼:
仍然是在做有 hidden variable $z$ 情況下的 MLE (Maximal Likelihood Estimation), 目前跟 EM algorithm 用法一樣.
與 EM 不同的是, 後驗概率 $p(z|x)$ 在 Markov chain 架構下是可得到公式解, 因此直接設定 auxiliary function $q(z)=p(z|x)$ 即可. 基於此, 可以進一步推導簡化, 見下段描述.
(Optional) 摘要一下 Diffusion Model 的 ELBO Loss 繼續簡化推導
最終 ELBO 目標函式為: 參考自 [What are Diffusion Models?]. 符號仍回到 Lil’Log, 最大的兩個差異是 Lil’Log 的 $p_\theta(\cdot)$ 在本文上面是寫成 $p(\cdot|\theta)$, 然後機率分佈 $q$ 在本文是用 $p$ 來表示 (本文的 $q$ 是用來指 auxiliary function 喔… 不一樣), 抱歉我知道很亂
$$\begin{align}
L_\text{VLB} &= \mathbb{E}_{q(\mathbf{x}_{0:T})} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \\
&= \mathbb{E}_q \Big[ \log\frac{\prod_{t=1}^T q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{ p_\theta(\mathbf{x}_T) \prod_{t=1}^T p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t) } \Big] \\
&= ... \\
&= \mathbb{E}_q [\underbrace{D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T))}_{L_T} + \sum_{t=2}^T \underbrace{D_\text{KL}(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t))}_{L_{t-1}} \underbrace{- \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)}_{L_0} ]
\end{align}$$ 整理一下
$$\begin{aligned}
L_\text{VLB} &= L_T + L_{T-1} + \dots + L_0 \\\text{where } L_T &= D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T)) \\L_t &= D_\text{KL}(q(\mathbf{x}_t \vert \mathbf{x}_{t+1}, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_t \vert\mathbf{x}_{t+1})) \text{ for }1 \leq t \leq T-1 \\L_0 &= - \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)
\end{aligned}$$ $L_T$ 是 constant 不用管 (因為最終都是 standard Gaussian)
$L_t$ 是 KL divergence 比較兩個 Gaussian distributions 因此有 closed form solution
其中經過一些推導可知 $q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \tilde{\boldsymbol{\mu}}(\mathbf{x}_t, \mathbf{x}_0), \tilde{\beta}_t \mathbf{I})$, where
$$\begin{aligned}
\tilde{\beta}_t &= {\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \\
\tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t, \mathbf{x}_0)&= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \mathbf{x}_0\\
\end{aligned}$$ (回憶到 $\beta_t$ 是 diffusion forward process 加 Gaussian noise 每次 iteration 的強度, 另外 $\alpha_t=1-\beta_t$, $\bar{\alpha}_t = \prod_{i=1}^T \alpha_i$)
另外注意到, 在訓練的時候我們是知道 $x_0$ 和 $x_t$ 的, 其中 $x_t$ 就是 forward process $t$ 次能得到. (實際上不會跑 $t$ 次 forward, 而是會一步到位), 所以正確答案的 $\tilde{\boldsymbol{\mu}}_t(x_t,x_0)$ 我們是知道的
而 $p_\theta(x_t|x_{t+1})$ 是我們的 NN (參數為 $\theta$) 的模型:
$$p_\theta(\mathbf{x}_{0:T}) = p(\mathbf{x}_T) \prod^T_{t=1} p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) \quad p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t))$$ 所以直接希望 NN predict 出來的 mean, $\mu_\theta(x_t,t)$, 跟 ground truth 的 mean, $\tilde{\boldsymbol{\mu}}_t(x_t,x_0)$, 的 MSE 愈小愈小即可. 另外其實我們不用 predict $\tilde\mu_t$, 我們 predict 他的 noise $\epsilon_t$ 就好, 一樣的意思
到這裡整個 DDPM 從 ELBO 簡化下來的訓練目標函式 $L_t^\text{simple}$ 就完成了:
$$\begin{aligned}
L_t^\text{simple}&= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\&= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big]
\end{aligned}$$ $\epsilon_t$ 是第 $t$ 次 forward process 時加的 Gaussian noise
注意到最小化 $L_t$ ($=L_t^\text{simple}$) 相當於希望我們的 NN $p_\theta(x_t|x_{t+1})$ 在給定 $x_{t+1}$ 的情況下能預測出 $x_t$, 但別忘了 $L_t$ loss 的目的是希望 $p_\theta(x_t|x_{t+1})\approx q(\mathbf{x}_t \vert \mathbf{x}_{t+1}, \mathbf{x}_0)$, 所以其實 NN 相當於也會預測出原始乾淨影像 $x_0$
因此可以想成每一步 denoise 過程中都會 隱含 預測出該步認為的乾淨影像 $x_0$, 但其實我們只需要最後 denoise 一步的乾淨影像輸出就可以
最後也可以參考李宏毅老師的解說也很清楚:
【生成式AI】Diffusion Model 原理剖析 [1], [2], [3], [4]
老師在第四個影片中嘗試解釋 sampling (DDPM 的 backward process) 時為何還要加個 Gaussian noise 項 (紅色框框部分):
這邊幫忙嚴謹補充一下, 其實就是 Score matching 使用 Langevin Dynamics 採樣的步驟 [ref]