隱變量的內插
還記得經典的 word embedding 特性嗎? 在當時 Mikolov 這篇經典的 word2vec 論文可讓人震驚了
$$\mathbf{e}_{king}+(\mathbf{e}_{man}-\mathbf{e}_{woman})\approx\mathbf{e}_{queen}$$ 這樣看起來 embedding space 似乎滿足某些線性特性, 使得我們後來在做 embedding 的內插往往採用線性內插:
$$\mathbf{e}_{new}=t\mathbf{e}_1+(1-t)\mathbf{e}_2$$ 讓我們把話題轉到 generative model 上面
不管是 VAE, GAN, flow-based, diffusion-based or flow matching models 都是利用 NN 學習如何從一個”簡單容易採樣”的分布, e.g. standard normal distribution $\mathcal{N}(\mathbf{0},\mathbf{I})$, 到資料分布 $p_{data}$ 的一個過程.
$$\mathbf{x}=\text{Decoder}_\theta(\mathbf{z}),\quad \mathbf{z}\sim\mathcal{N}(\mathbf{0},\mathbf{I})$$
Lil’Log “What are Diffusion Models?” Fig. 1. 的 variable $\mathbf{z}$ 實務上大多使用 $\mathcal{N}(\mathbf{0},\mathbf{I})$ 的設定
(借用 Jia-Bin Huang 影片的圖 How I Understand Diffusion Models 來舉例)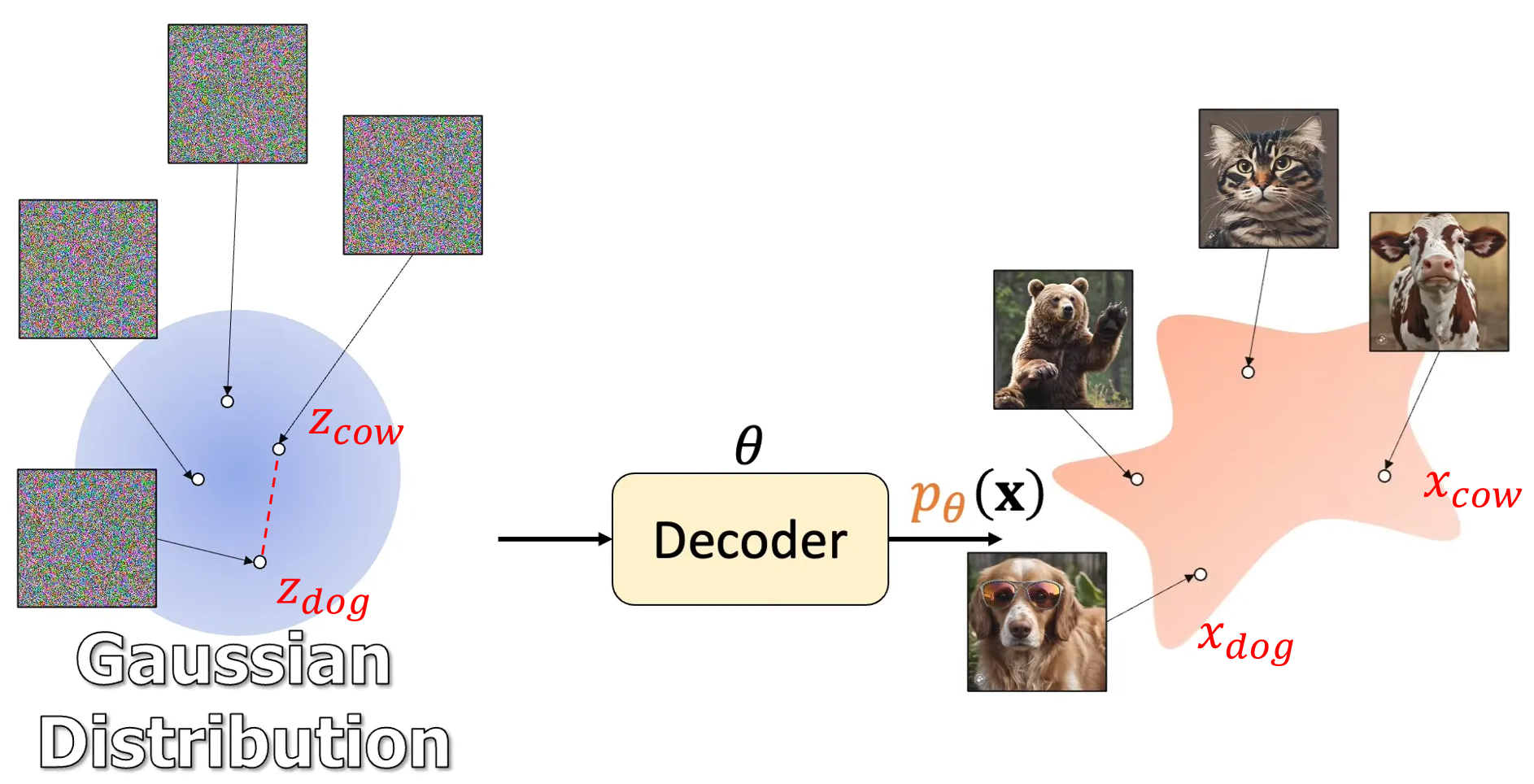
因此如果我們想產生狗和牛的混合體, 是不是可以這樣作?
$$\text{Decoder}_\theta(t\mathbf{z}_{dog}+(1-t)\mathbf{z}_{cow}), \quad t\in[0,1]$$ 答案是不行, 效果不好. 那具體怎麼做呢? 其實應該這麼做 [1]
$$\text{Decoder}_\theta(\cos(t\pi/2)\mathbf{z}_{dog}+\sin(t\pi/2)\mathbf{z}_{cow}), \quad t\in[0,1]$$ 要使用 spherical linear interpolation [2] 這種內插方式
或簡單說球面內插: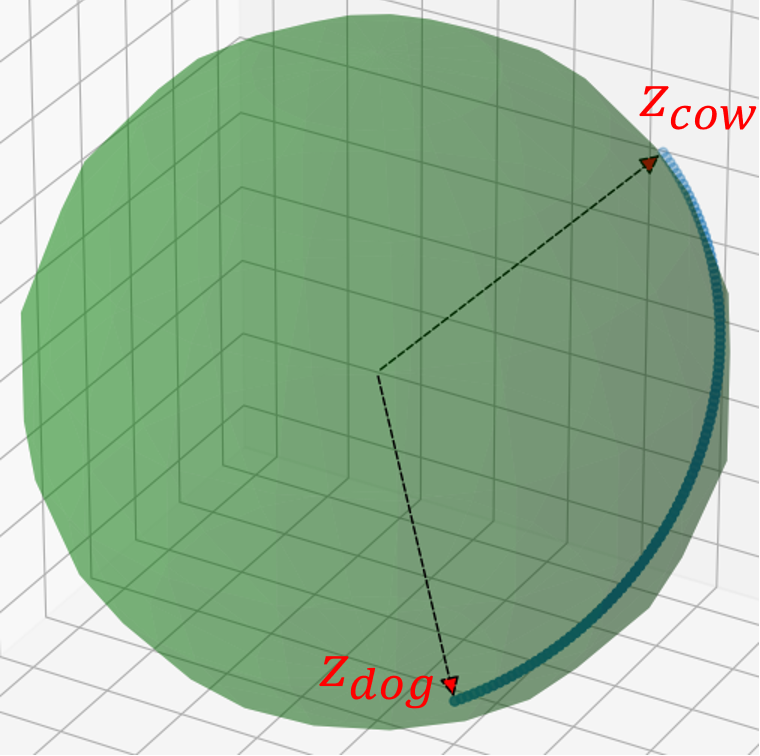
為什麼使用線性內插不好, 而需使用球面內插呢?
聰明的讀者或許會猜因為 $\mathbf{z}$ 是 normal distribution 或許是因為空間不是那麼線性的關係?
但就算使用線性內插好了, 也應該是符合 normal distribution 會產生的 sample 點阿?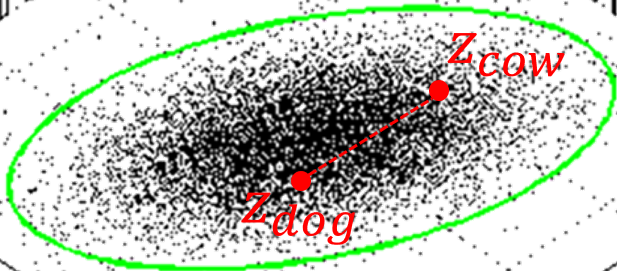
所以究竟為何線性內插效果不好?
要回答這問題就牽涉到高維度下的常態分佈長相, 可能會跟你想的不一樣, 挺反直覺的!
高維度下的常態分佈
先問一個問題, 我們對一個常態分佈 $\mathcal{N}(\mathbf{0},\sigma^2\mathbf{I})$ 採樣, 採樣出來的點大概會落在什麼位置?
我想大部分的回答都是集中在 mean 附近吧.
對, 在低維度下是對的. 但如果維度 $D$ 很大, 其實幾乎只會落在 $\sqrt{D}\sigma$ 的距離的球面上
[3] 提到, 對常態分佈, 我們將 Cartesian coordinate 換成角度和距離的座標, 並把角度全部積分只留下距離後得到”距離 $r$ 的 pdf”:
$$p(r)=\frac{S_Dr^{D-1}}{(2\pi\sigma^2)^{D/2}}\exp\left({-\frac{r^2}{2\sigma^2}}\right)$$ 其中 $S_D$ 是單位圓的球面面積, 跟 $r$ 無關視為常數即可
重新整理一下把跟 $r$ 無關的常數項合併為另一個常數 $c$
$$p(r)=cr^{D-1}\exp\left({-\frac{r^2}{2\sigma^2}}\right)$$ 我們微分=0 並使用 chain rule 分析下去:
$$\frac{d}{dr}p=\frac{d}{dr}cr^{D-1}\exp\left({-\frac{r^2}{2\sigma^2}}\right)=0 \\
\Longrightarrow r^2=\sigma^2(D-1)= \sigma^2D,\quad D\rightarrow\infty \\
\Longrightarrow r=\sqrt{D}\sigma,\quad D\rightarrow\infty$$ 這告訴我們 $p(r)$ 存在一個極大值! (可以驗證二次微分來確定是極大或極小值)
也就是說在 $\hat{r}=\sqrt{D}\sigma$ 的距離下 density $p(\hat{r})$ 是最大的
[3] 繼續分析到在 $\hat{r}$ 附近擾動一下 ($\varepsilon\ll\hat{r}$) 的 density 變化為:
$$p(\hat{r}+\varepsilon)
=p(\hat{r})\exp\left({-\frac{3\varepsilon^2}{2\sigma^2}}\right)$$ 白話就是在 $\hat{r}$ 附近的 density 會指數性下降! 下圖為示意圖: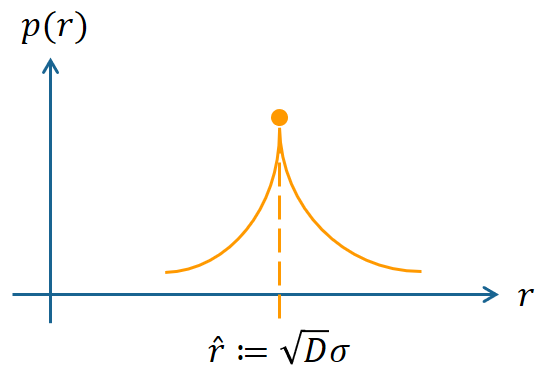
因此我們考慮累積分佈函數 (cdf) 會發現在 $\hat{r}$ 的值會突然從 $0$ 飆到 $1$.
高斯分布的 pdf 幾乎存在 $\hat{r}=\sqrt{D}\sigma$ 這個半徑的圓表面上!
💡 數學分析是一回事, 如果想更值觀的理解為何如此, 不妨這麼想. 這些 $D$ 個維度只要有任一維度採樣不在 mean 附近, 整個 $\mathbf{z}$ 就不會在 mean 了. 所以當維度一高, 似乎不在 mean 也很合理.
回答為何要球面內插
在來回頭看狗和牛的線性內插
$$\text{Decoder}_\theta(t\mathbf{z}_{dog}+(1-t)\mathbf{z}_{cow}), \quad t\in[0,1]$$ 因為 $\mathbf{z}_{dog}$ 和 $\mathbf{z}_{cow}$ 是從 $\mathcal{N}(\mathbf{0},\sigma^2\mathbf{I})$ 採樣出來的, 由上面一段討論我們知道, 他們有非常高的機率是在那個半徑為 $\hat{r}$ 的圓球表面採樣出來的
做了線性內插出來的值, 其實根本不符合從 $\mathcal{N}(\mathbf{0},\sigma^2\mathbf{I})$ 採樣出來的點.
所以使用球面內插就清楚了然了
$$\text{Decoder}_\theta(\cos(t\pi/2)\mathbf{z}_{dog}+\sin(t\pi/2)\mathbf{z}_{cow}), \quad t\in[0,1]$$
後記
在看蘇神的 生成扩散模型漫谈(四):DDIM = 高观点DDPM 時看到使用球面內插. 突然間跟學生時代看的 PRML book 裡提到高微度常態分佈的長相 [3] 連結起來, 這種跨越好幾年把兩個東西連結在一起的感覺真有意思!
總之看到高維度的常態分佈, 腦袋要想的就是這個分布長的就像是只有蛋殼的蛋.
Reference
- 生成扩散模型漫谈(四):DDIM = 高观点DDPM, 或 DDIM 論文 Appendix D.5 裡面都有提及使用球面內插
scipy.spatial.geometric_slerp, wiki slerp- Bishop PRML book Chapter 1 的 excercise 1.20
- 一些圖的.pptx