下一篇: 嘗試理解 Flow Matching
如果你跟我一樣看 flow matching 論文時, 在還在說明預備知識的地方就陣亡了, 別擔心你不孤單! 我也死在那裡.
論文裡很多地方用到了 Continuity Equation 來推導. 這個定理也相當於是一個核心概念.
抱持一定要了解清楚的想法, 結果是學習到了美妙的 Gauss’s Divergence Theorem 和 Continuity Equation!
通了! 通暢了! …. 我指任督二脈
🎉 也剛好這是本部落格第 100 篇的文章, 就決定用這個主題了! 🎉
讓我們進入這美妙的 “物理 feat 機器學習 (Physics x ML)” 的世界吧!
(本文用的圖檔: div_fig.drawio)
我們分成幾大段落來說明:
A. Vector Field
B. Divergence (散度)
C. Gauss’s Divergence Theorem
D. Mass Conservation or Continuity Equation
E. 跟 Flow Matching 有啥關聯?
A. Vector Field
這是從中央氣象局的風場圖擷取的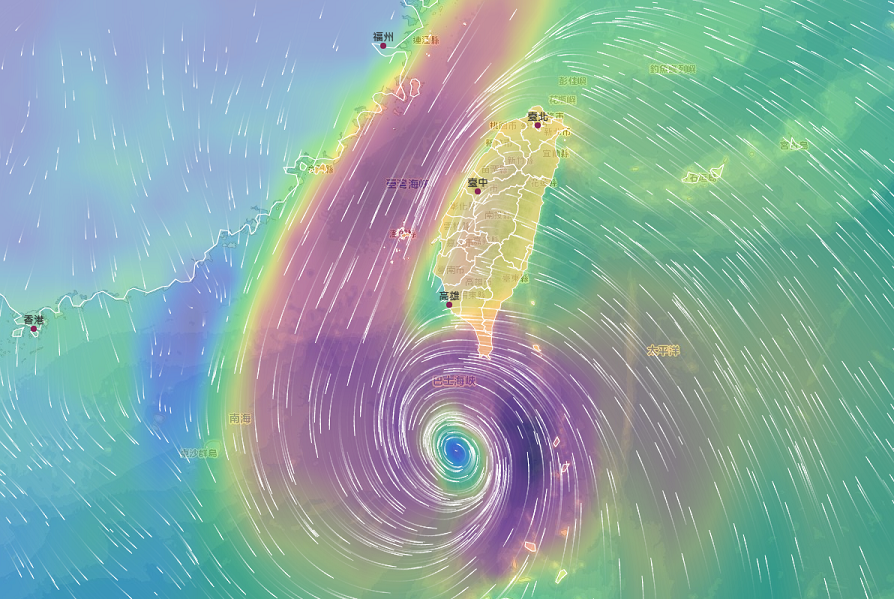
類似的圖想我大家應該不陌生, 顯示了每個位置 $(x,y)$ 對應的風速”向量” $\vec{F}\in\mathbb{R}^2$, i.e. $\vec{F}:\mathbb{R}^2\rightarrow\mathbb{R}^2$:
$$\vec{F}(x,y)=F_1(x,y)\vec{i}+F_2(x,y)\vec{j}$$ 其中 $\vec{i},\vec{j}$ 分別是 $x,y$ 軸的單位向量. 顏色代表該向量個強度.
再舉個例子 (來源)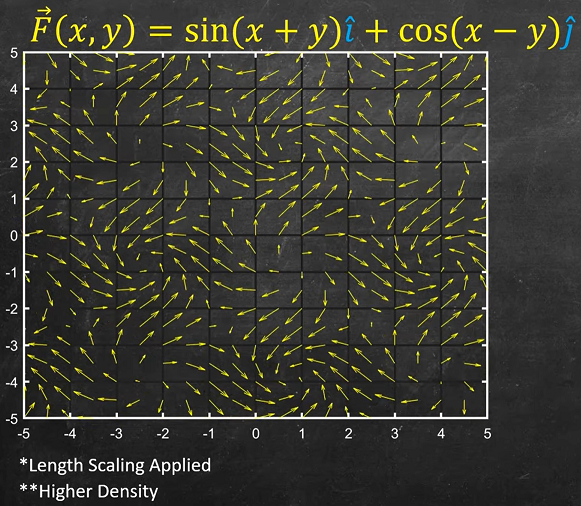
箭號長度表示向量強度
所以 $n$ 維的 vector field 為 $\vec{F}:\mathbb{R}^n\rightarrow\mathbb{R}^n$
B. Divergence (散度)
還記得最開始學積分的時候嗎?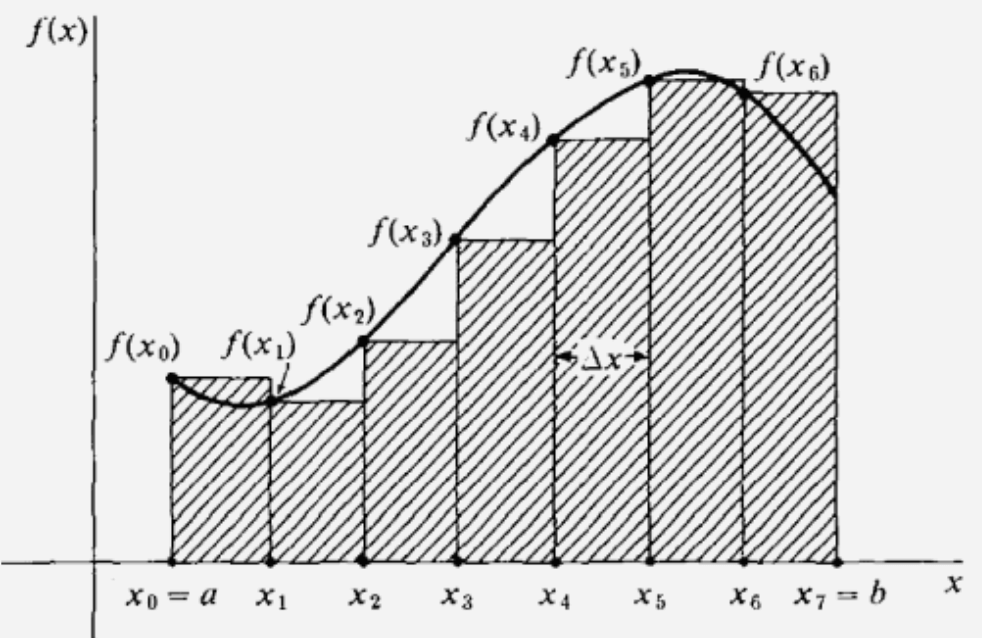
我們對 domain 切成等均的段落, 並且函數值取每個段落”左邊的值”, 然後乘上段落長度 $\Delta x$.
例如上圖 domain 為 $[a,b]$ 切成 $7$ 段, i.e. $[a=x_0,x_1,…,x_7=b]$. 第 $i$ 段 $[x_{i-1},x_i]$ 我們取左邊的函數值 $f(x_{i-1})$.
大家應該都不陌生, 不過這裡要說的是把問題拆分的兩點技巧等等會用到:
1. 切等均段落
2. 取左邊函數值
想像 2 維空間, 我們有一個 vector field $\vec{F}:\mathbb{R}^2\rightarrow \mathbb{R}^2$, i.e.
$$\vec{F}(x,y)=F_1(x,y)\vec{i}+F_2(x,y)\vec{j}$$ 如同上述積分一樣, 先將空間切成等均方形的面積, 令左下角座標為 $(x_0,y_0)$, 右上角座標為 $(x_0+\Delta x,y_0+\Delta y)$, 觀察其中一塊方形 $A$ 和其對應的 vector field $\vec{F}$: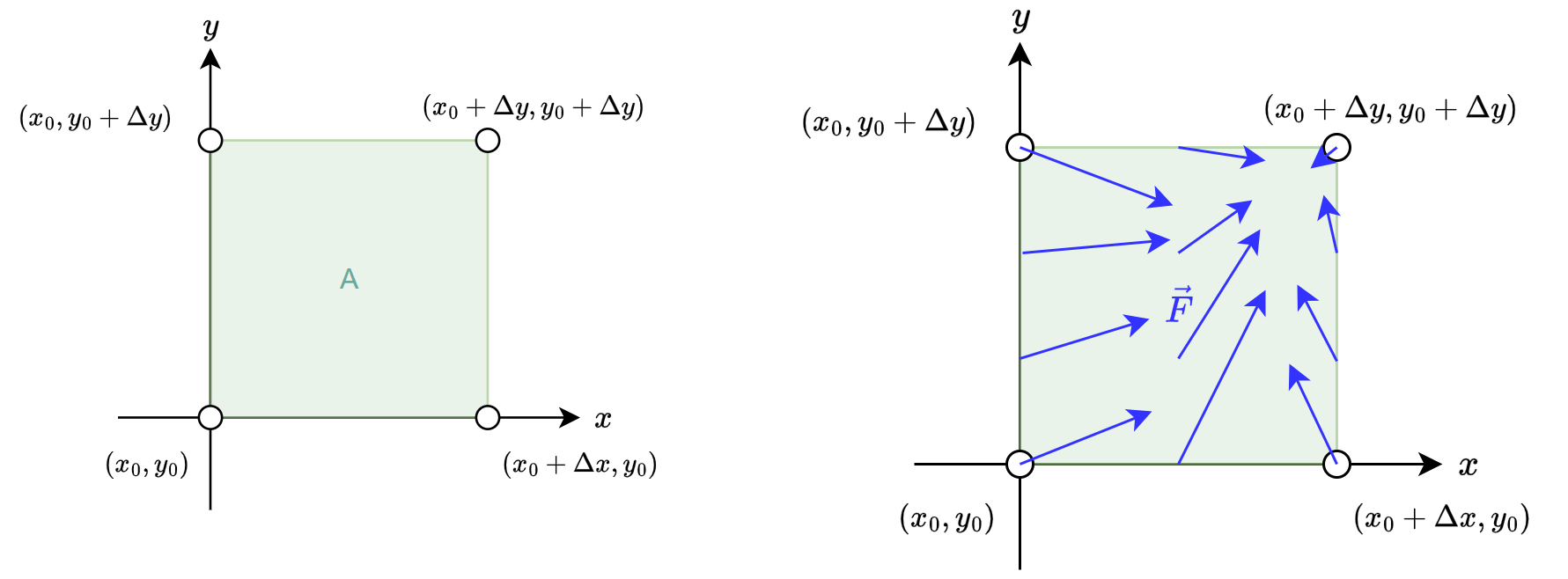
我們希望計算 $\vec{F}$ 對這塊面積 $A$ 的淨流出 (流入) 量
注意到只需考慮邊界, 因為面積內的流入/出不影響總體面積的淨流入/出量
首先看左邊界, 並且如同做積分時選取左區段的函數值一樣, 我們選擇左下角這點的 vector field 值 $\vec{F}(x_0,y_0)$.
左邊界淨流出量
$\vec{F}(x_0,y_0)$ 要能對左邊界產生影響, 只能是 $x$ 方向, 也就是與 $\vec{i}$ 內積後的向量
$$<\vec{F}(x_0,y_0),\vec{i}>\vec{i}$$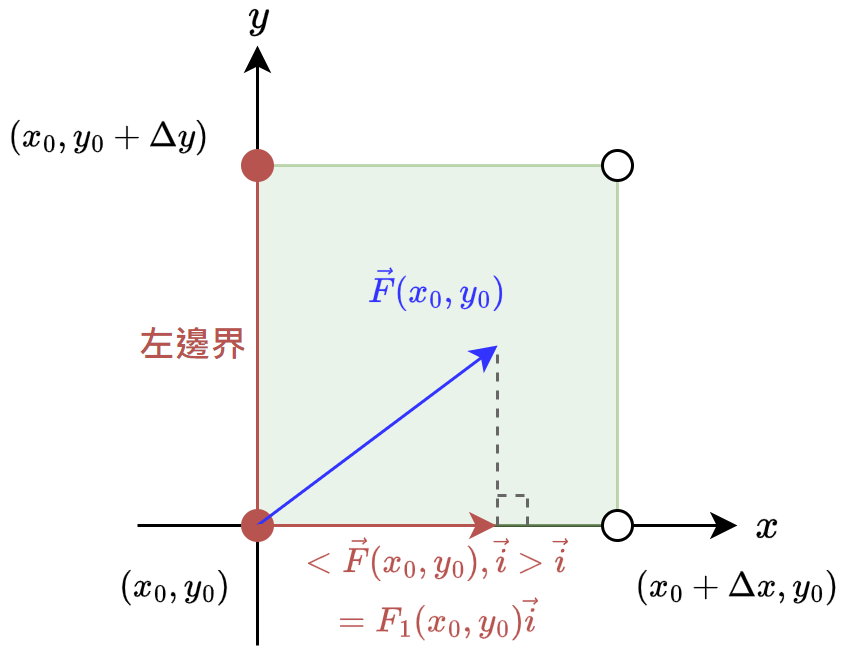 
為什麼呢? 因為與 $y$ 方向 $\vec{j}$ 內積產生的向量, 只會在 $y$ 軸上流動 (左邊界上移動), 不會對方型 $A$ 有流入流出的影響.
因此左邊界淨流出量為:
$$\begin{align}
<\vec{F}(x_0,y_0),\vec{i}>\Delta y=F_1(x_0,y_0) \Delta y
\end{align}$$
如同在積分用的技巧一樣, 我們對線段 $\Delta y$ 只取了一點函數值代表, 並與線段長度 $\Delta y$ 乘起來
右邊界淨流出量
同理考慮右邊界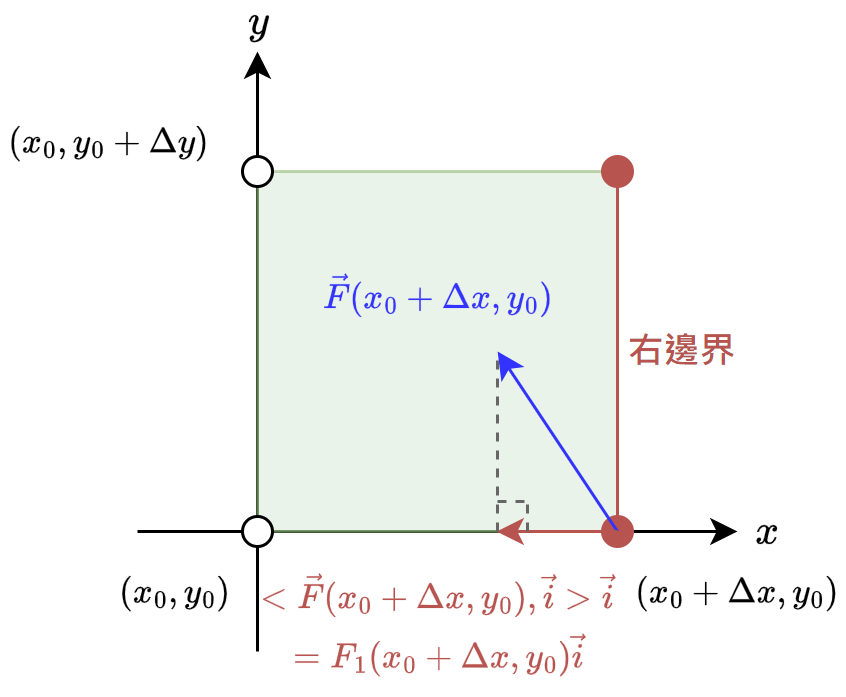
右邊界淨流出量為:
$$\begin{align}
<\vec{F}(x_0+\Delta x,y_0),\vec{i}>\Delta y=F_1(x_0+\Delta x,y_0) \Delta y
\end{align}$$
X 軸方向淨流出量
注意到我們定義的是流出量, 不是流入量
因此如果左邊界乘起來的的結果 (1) 是正的代表是流入, 不是流出, 所以若我們定義的是”流出”量, 則 (1) 的結果要多乘一個負號
而右邊界的結果 (2) 是正的就是代表流出
所以 $x$ 軸方向的淨流出量應該為 (2) 加上乘負號的 (1):
$$\begin{align}
[F_1(x_0+\Delta x,y_0) - F_1(x_0,y_0)] \Delta y
\end{align}$$
Y 軸方向淨流出量
同理我們可得 $y$ 軸方向的淨流出量:
$$\begin{align}
[F_2(x_0,y_0+\Delta y) - F_2(x_0,y_0)] \Delta x
\end{align}$$
單位面積淨流出量
方形面積 $A$ 的總淨流出量為 (3)+(4):
$$[F_1(x_0+\Delta x,y_0) - F_1(x_0,y_0)] \Delta y + [F_2(x_0,y_0+\Delta y) - F_2(x_0,y_0)] \Delta x$$ 換算 ”單位面積” 的淨流出量為 (除以面積 $\Delta A = \Delta x\Delta y$):
$$\begin{align}
\frac{F_1(x_0+\Delta x,y_0) - F_1(x_0,y_0)}{\Delta x} + \frac{F_2(x_0,y_0+\Delta y) - F_2(x_0,y_0)}{\Delta y}
\end{align}$$ 對面積 $\Delta A\rightarrow 0$ 取極限後, 代表的是該 “點 $(x_0,y_0)$” 的單位面積淨流出量!
$$\lim_{\Delta A\rightarrow0} \frac{F_1(x_0+\Delta x,y_0) - F_1(x_0,y_0)}{\Delta x} + \lim_{\Delta A\rightarrow0}\frac{F_2(x_0,y_0+\Delta y) - F_2(x_0,y_0)}{\Delta y} \\ \Longrightarrow \frac{\partial F_1}{\partial x}(x_0,y_0) + \frac{\partial F_2}{\partial y}(x_0,y_0) \\ = {\color{orange}{\left<\left[ \begin{array}{c} \partial/\partial x \\ \partial/\partial y \end{array} \right], \left[\begin{array}{c} F_1 \\ F_2 \end{array}\right]\right>}}(x_0,y_0) \\ ={\color{orange}{\nabla\cdot\vec{F}}}(x_0,y_0)$$ (注): 內積用 $<\vec{a},\vec{b}>$ 或 $\vec{a}\cdot\vec{b}$ 表示都可以
Divergence 散度物理意義
考慮 $n$ 維的 vector field:
$$\vec{F}(x_1,x_2,...,x_n)=(F_1,F_2,...,F_n)$$ 定義散度算子為 $\nabla\cdot$ 或 $\text{div}$:
$$\begin{align}
{\color{red}{\text{div}\vec{F}=\nabla\cdot\vec{F} = \sum_{i=1}^n\frac{\partial F_i}{\partial x_i}}}
\end{align}$$ 重要的是記住其物理意義:
💡 $\text{div}\vec{F}(\vec{x})$ 表示, 點 $\vec{x}$ 的”單位體積”向量場的淨流出量
💡 $\text{div}\vec{F}(\vec{x})$ 表示, 點 $\vec{x}$ 的”單位體積”向量場的淨流出量
💡 $\text{div}\vec{F}(\vec{x})$ 表示, 點 $\vec{x}$ 的”單位體積”向量場的淨流出量
C. Gauss’s Divergence Theorem
考慮空間中有一個體積 $V$, 有封閉的表面 $\partial V$. 如下圖 (擷取 wiki: Divergence theorem):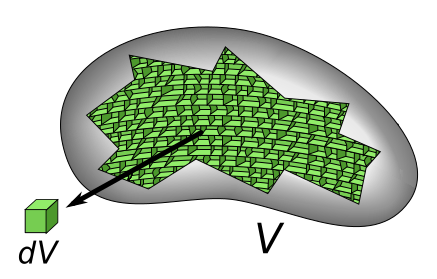
同樣的手法, 我們將 $V$ 用很多很小的 cubes, $dV$, 組合起來
接著請想像有一個向量場 $\vec{F}:\mathbb{R}^3\rightarrow \mathbb{R}^3$ 穿過這個 $V$.
❓我們要探討的問題是: 向量場 $\vec{F}$ 作用於 $V$ 產生的”總”淨流出量為何?
用體積分
阿! 要算 “總”淨流出量, 而我們知道散度定義是每個”點”的單位淨流出量, 那把每個點的散度加總起來不就好了嗎? i.e. 用體積分.
$$\begin{align}
\iiint_V\nabla\cdot\vec{F}dV
\end{align}$$ 👏🏻 答對了!
不知道各位有沒有聽過一句話:
看山是山; 看山不是山; 看山還是山
向量場 $\vec{F}$ 作用於 $V$ 產生的”總”淨流出量真的是 (7) 嗎?
我們剛剛的直覺想法在現階段認為是對的, 這是思考的第一步: 看山是山
接著想想…
看山不是山
思考一下相鄰的兩個 cubes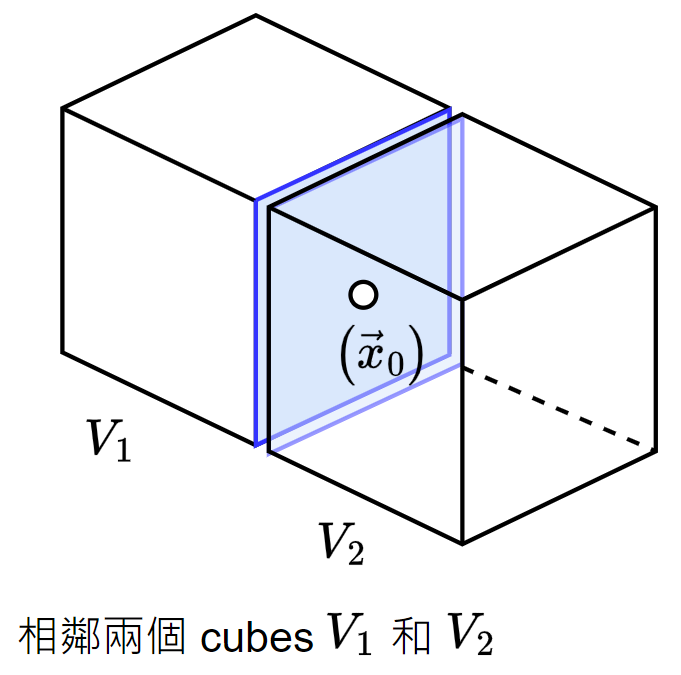
我們剛剛的想法是把 $V_1$ 和 $V_2$ 的 divergence 相加起來
考慮在相接的面上的一個點 $\vec{x}_0=(x_0,y_0,z_0)$, $\vec{x}_0$ 在 $V_1$ 被算了一次, 然後在 $V_2$ 又被算了一次, 這樣不就重複計算了嗎?? 所以剛剛的直覺做法錯了嗎?
hmm…看山不是山
繼續思考看看…
看山還是山
考慮 vector field $\vec{F}$ 是 continuous 的, 則
$$\begin{align}
\lim_{
\vec{x}\rightarrow\vec{x}_0, \vec{x}\in {\color{orange}{S_1}}
}
\vec{F}(\vec{x}) = \lim_{
\vec{x}\rightarrow\vec{x}_0, \vec{x}\in {\color{orange}{S_2}}
}\vec{F}(\vec{x})
\end{align}$$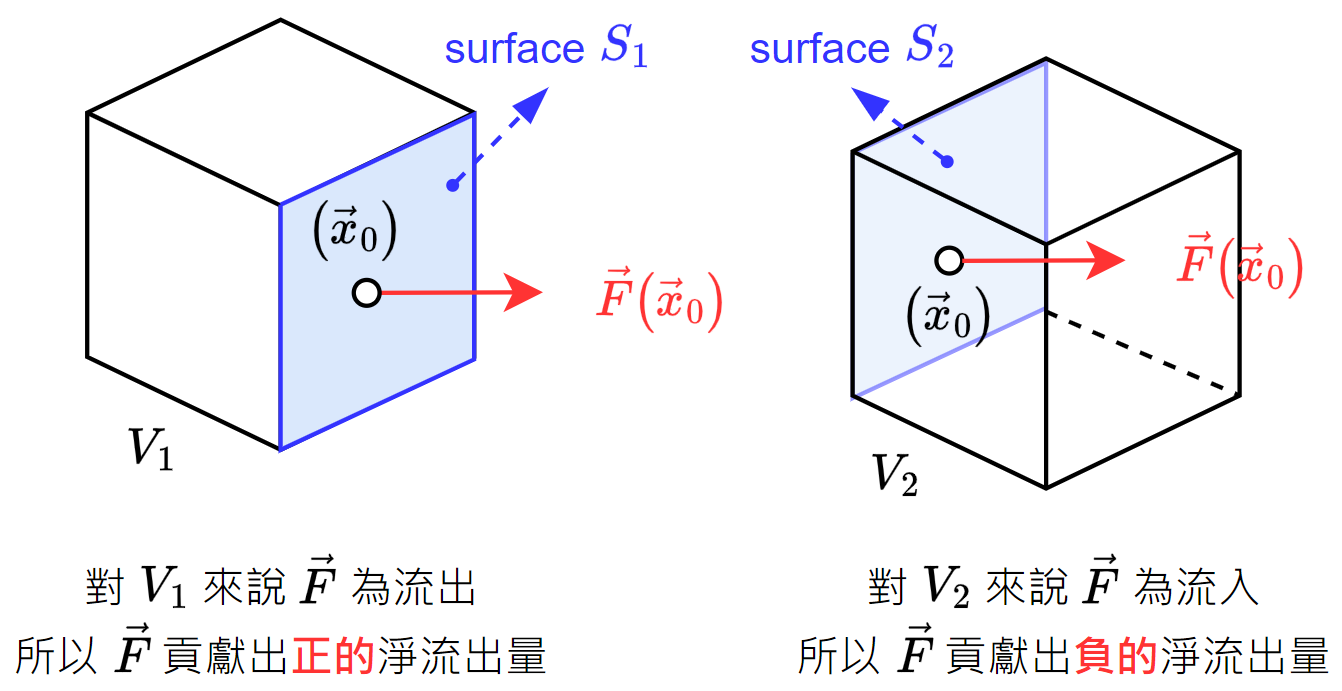 
則對 $V_1$ 來說 $\vec{F}(\vec{x}_0)$ 是流出的向量場, $V_2$ 則是流入的向量場, 兩邊自己算 divergence 相加的話剛好一正一負, 互相抵銷!
所以是用體積分對的
向量場 $\vec{F}$ 作用於 $V$ 產生的”總”淨流出量為:
$$\begin{align}
\iiint_V\nabla\cdot\vec{F}dV
\end{align}$$ 山還是那個山
用表面積分
其實要回答這個問題: “向量場 $\vec{F}$ 作用於 $V$ 產生的”總”淨流出量為何?” 還可以從表面積分出發!
一樣借用 wiki 的圖 [Flux]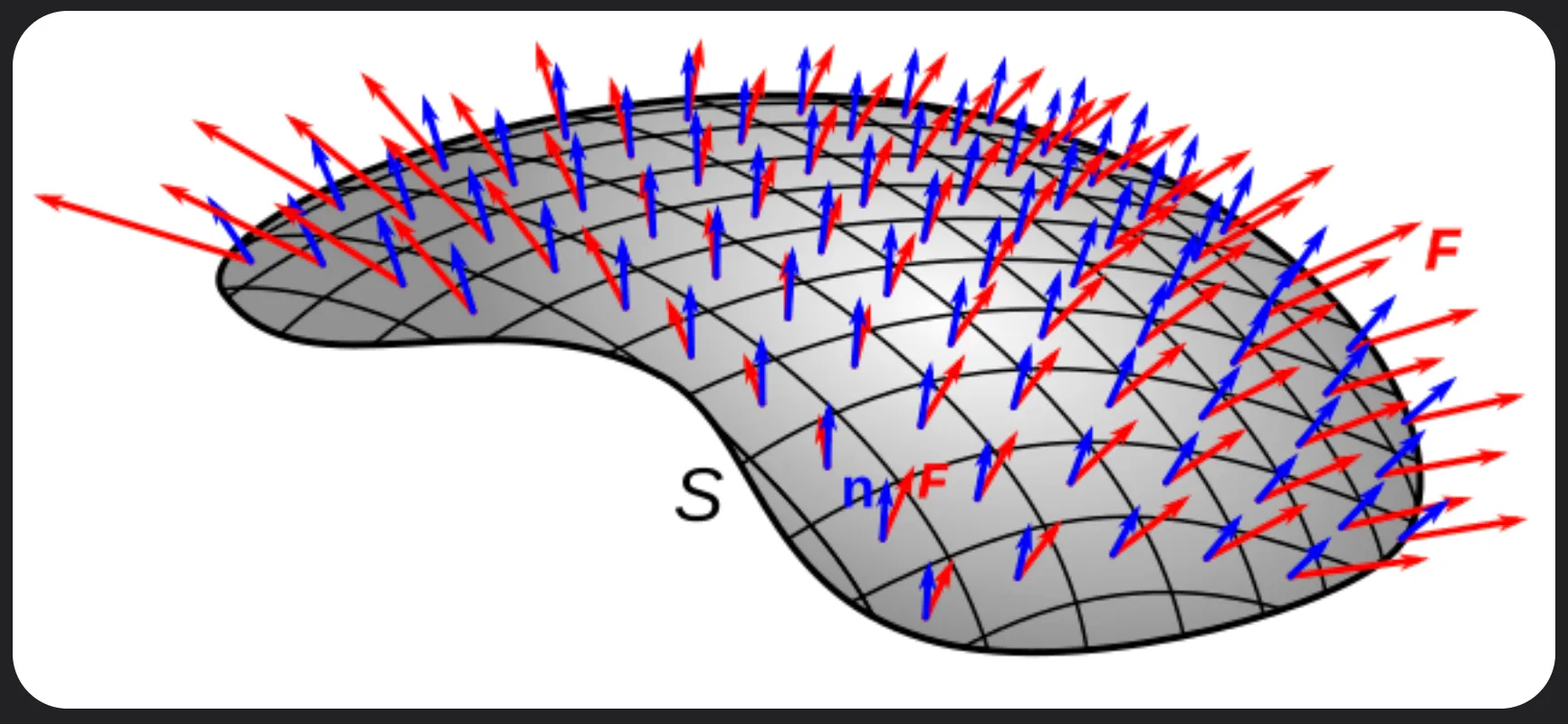
$\vec{F}$ 穿過 surface $S$ 的大小, 只能看 $\vec{F}$ 與 surface 的 normal vector $\vec{n}$ 平行的向量分量
這是因為如果看與 $\vec{n}$ 垂直的分量的話, 只會流通於 surface $S$, 不會有流入流出 (穿過) $S$ 的作用.
所以我們只需要看 $\vec{F}\cdot\vec{n}$ 這個分量的結果.
注意因為 normal vector $\vec{n}$ 是朝外指出表面的, 所以 $\vec{F}\cdot\vec{n}$ 已經是流出量的意思了
然後對表面的每個點上述分量都加起來 (表面積分), 我們不就也同樣得到了 “向量場 $\vec{F}$ 作用於 $V$ 產生的總淨流出量” 了嗎?
寫成數學式子為:
$$\begin{align}
\iint_S \vec{F}\cdot\vec{n}dS
\end{align}$$ 有時候會看到 $\oiint_S$ 的寫法, 其實中間那個圈只是用來表明 $S$ 是封閉的 surface 而已.
散度的體積分等於表面積分
物理意義上 (9) 等於 (10)! 而這就是大名鼎鼎的高斯散度定理 Gauss’s Divergence Theorem:
$$\begin{align}
{\color{red}{\iiint_V\nabla\cdot\vec{F}dV = \iint_S \vec{F}\cdot\vec{n}dS}}
\end{align}$$ 有時候表面積分不好算, 可藉由散度定理轉換成體積分會變得好算很多.
D. Mass Conservation or Continuity Equation
Gauss’s Divergence Theorem 的一個重要應用是可以推導出 Mass conservation!
這一段可能複雜一些, 快結束了! 快碰到核心了!
定義 total mass in $V$ 為: $$\text{Total Mass}:=\iiint_V\rho dV$$ 其中 $\rho$ 為密度: $\rho(x,y,z,t)$, 或寫 $\rho(\vec{x},t)$, 注意到密度也跟時間有關, 如噴射機的空氣密度會變化
所以 total mass 對時間的變化為: $$\begin{align}
\frac{d}{d t}\iiint_V\rho dV
\end{align}$$ (12) 如果是正的表示 mass 增加, 負的表示 mass 減少
注意到 (12) 這裡不寫 $\partial/\partial t$ 的原因是對體積分完後, 空間的 $\vec{x}$ 變量已經不見了, 只剩時間 $t$, 因此寫 total derivative
考慮向量場 $\vec{F}_t$ 定義為粒子的移動速度, 注意到我們有下標 $t$ 表示向量場可隨時間變化
💡 因此對於 $\nabla\cdot\vec{F}_t(\vec{x}_0)$ 物理意義就是: 在時間 $t$ 時, 位置 $\vec{x}_0$ 的”單位體積”粒子的淨流出量
💡 如果考慮密度再計算散度的話, i.e. $\nabla\cdot(\rho(\vec{x}_0)\vec{F}_t(\vec{x}_0))$, 就變成: 在時間 $t$ 時, 位置 $\vec{x}_0$ 的質量淨流出量!
如同文章之前描述的觀念 volume $V$ 的質量變化只會發生在表面的質量變化 (因為內部的質量變化不影響 total mass)! 如同我們上一段說明表面積分的概念, 用數學表示為:
$$\begin{align}
\iint_S\rho\vec{F}_t\cdot\vec{n}dS
\end{align}$$ (13) 如果是正的表示 mass 減少, 負的表示 mass 增加 (因為 normal vector $\vec{n}$ 指向表面外)
同樣的, 物理上 (12) 跟 (13) 對質量的描述是相同的, 所以:
$$\begin{align}
\frac{\partial}{\partial t}\iiint_V\rho dV = -\iint_S\rho\vec{F}_t\cdot\vec{n}dS
\end{align}$$ 根據 Gauss’s Divergence Theorem (11) 可以改寫 (14) 的 RHS:
$$\begin{align}
\frac{\partial}{\partial t}\iiint_V\rho dV = -\iiint_V\nabla\cdot(\rho\vec{F}_t)dV \\
\Longrightarrow \iiint_V\left(
\frac{\partial\rho}{\partial t}+\nabla\cdot(\rho\vec{F}_t)
\right)dV=0
\end{align}$$ 因為 (16) 對任何 closed volume $V$ 都成立, 所以得到如下的 Mass Continuity Equation:
$$\begin{align}
{\color{orange}{\frac{\partial\rho}{\partial t}}}
+
{\color{green}{\nabla\cdot(\rho\vec{F}_t)=0}}
\end{align}$$ 叫 continuity equation 是因為不要忘記我們有個條件就是 $\rho\vec{F}_t$ 必須是連續的, equation (8), 否則 Gauss Divergence Theorem 就不成立
這就是質量守恆的 Partial Differential Equation (PDE)
- ${\color{orange}{\partial \rho(\vec{x}_0,t)/\partial t}}$ 表示位置 $\vec{x}_0$ 隨時間變化的密度變化, 正的表示質量會增加
- ${\color{green}{\nabla\cdot(\rho(\vec{x}_0,t)\vec{F}_t(\vec{x}_0))}}$ 表示在時間 $t$ 時, 位置 $\vec{x}_0$ 的質量淨流出量! 正的表示質量會減少
而 ${\color{orange}{\partial \rho(\vec{x}_0,t)/\partial t}}$ 造成的質量增加要等於 ${\color{green}{\nabla\cdot(\rho(\vec{x}_0,t)\vec{F}_t(\vec{x}_0))}}$ 造成的質量減少, 此為 (17) 代表的物理意義.
👏🏻 質量守恆!
E. 跟 Flow Matching 有啥關聯?
把機率密度函數想成一個真實的物體, 物體密度 $\rho(x)$ 就是我們的機率密度 $p(x)$.
只是該物體是總質量為 $1$ 而已 (因為機率總和為 $1$)
我們從一個常態分佈出發… 中間不管經過怎樣的分佈變化, 最終假設我們能變化成目標機率分佈 $q(x)$.
整個過程 Continuity Equation, 或說 Mass Convervation (17) 都是一直要滿足的!
因為不管怎麼變都還是機率分佈, 總質量都維持不變 $1$.
這個核心觀念會貫穿整個 Flow matching 論文裡. 至此終於可以開始啃 flow matching 了!
下回真正開始講解 flow matching 論文: 嘗試理解 Flow Matching