筆記來源 **[DeepBayes2019]: Day 5, Lecture 3. Langevin dynamics for sampling and global optimization 前半小時. 非常精彩!**
粒子 $x$ follow Langevin dynamics 的話: $$x-x'=-\nabla U(x')dt+\mathcal{N}(0,\sigma^2dt)$$ $x$ 隨時間的機率分布 $p_t(x)$ 會滿足 Fokker-Planck equation 這種 Stochastic Differential Equation (SDE) 的形式:
$$\frac{\partial }{\partial t}p_t(x)=\nabla p_t(x)^T\nabla U(x)+p_t(x)\text{div}\nabla U(x)+\frac{1}{2}\sigma^2\nabla^2p_t(x)$$ 而從 F-P equation 我們可以發現最後 $t\rightarrow\infty$ 時某種設定下會有 stationary 分佈.
而如果將要採樣的目標分佈 $p(x)$ 設定成這種 stationary 分佈的話.
由於是 stationary 表示就算繼續 follow Langevin dynamics 讓粒子 $x$ 移動 (更新), 更新後的值仍然滿足目標分佈 $p(x)$, 因此達到採樣效果!
而這也是 Denoising Diffusion Probabilistic Models (DDPM) 做採樣時的方法.
接著詳細記錄 Langevin dynamics, Fokker-Planck equation 推導, 以及 stationary 分佈和採樣方法.
如果讀者知道 Continuity equation 的話, 應該會發現與 F-P equation 非常相似. 它們的關聯可以參考 “Flow Matching for Generative Modeling” 論文的 Appendix D.
Langevin Dynamics
從 Langevin dynamics 出發, 考慮如下的 Stochastic Differential Equation (SDE) 其中 $X(t)$ 是 random process:
$$\begin{align}
dX(t)=\underbrace{-\nabla U(X(t))dt}_{\text{Force}}+\underbrace{\sigma dBt}_{\text{random fluctuation}}
\end{align}$$ 其中 $B_t$ 是 Brownian motion, (或稱 Wiener process)
對它做離散逼近:
$$\begin{align}
X_{t+1}-X_t=-dt\nabla U(X_t)+\sigma\sqrt{dt}\mathcal{N}(0,I)
\end{align}$$ 注意到 $B_{t+dt}-B_t\sim\mathcal{N}(0,dt)=\sqrt{dt}\mathcal{N}(0,I)$.
下圖顯示粒子使用 (1) 的移動軌跡 (來源):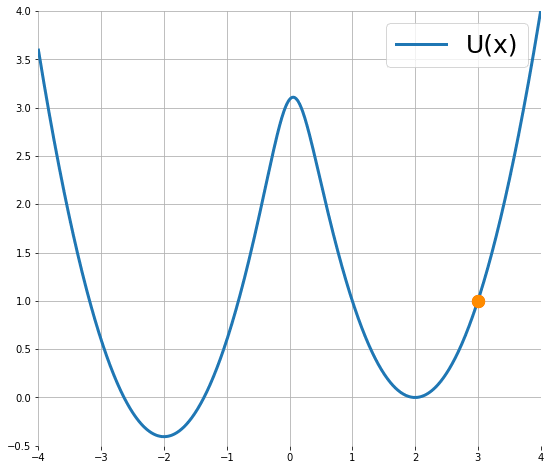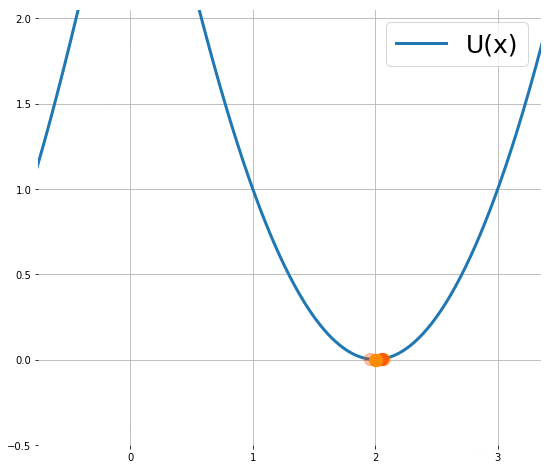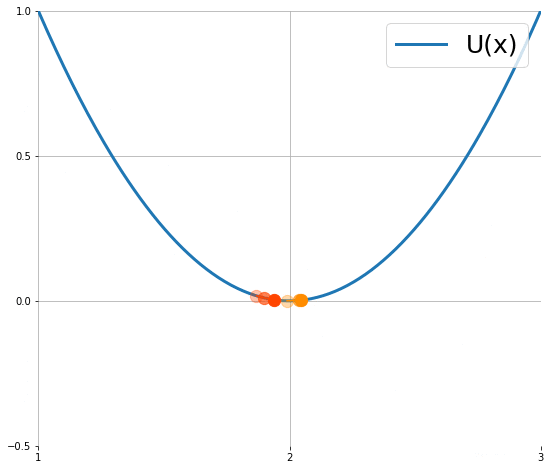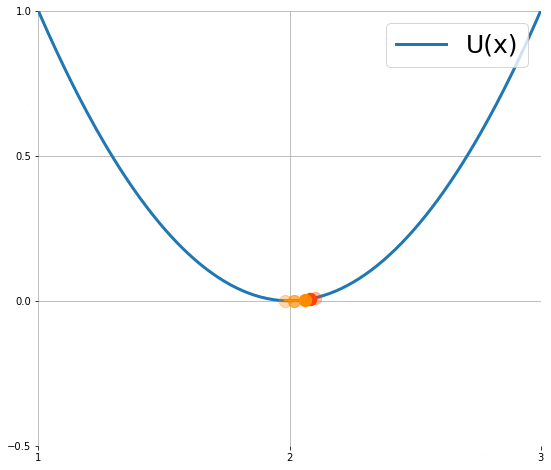
這個 SDE 其實跟 Machine Learning 的 Gradient Descent 很有關聯, 改寫一下:
$$\begin{align}
W_{t+1}-W_t=-\varepsilon\nabla \mathcal{L}(W_t)+\sigma\sqrt{\varepsilon}\mathcal{N}(0,I)
\end{align}$$ 其中 $W_t$ 表示第 $t$ 次 iteration 時的 parameter, $\mathcal{L}$ 表示 loss function.
會發現就是 gradient descent 公式多一個 random 項.
Fokker-Planck Equation
Fokker-Planck equation 描述了如果 partical $x$ 的移動遵從 Langevin dynamics, 則 density 隨著時間的變化, i.e. $\frac{\partial}{\partial t}p_t(x)$, 可以被描述出來
$$\frac{\partial }{\partial t}p_t(x)=\nabla p_t(x)^T\nabla U(x)+p_t(x)\text{div}\nabla U(x)+\frac{1}{2}\sigma^2\nabla^2p_t(x)$$ 其中 $\text{div},\nabla^2$ 為 divergence 和 Laplace operators. 圖片來源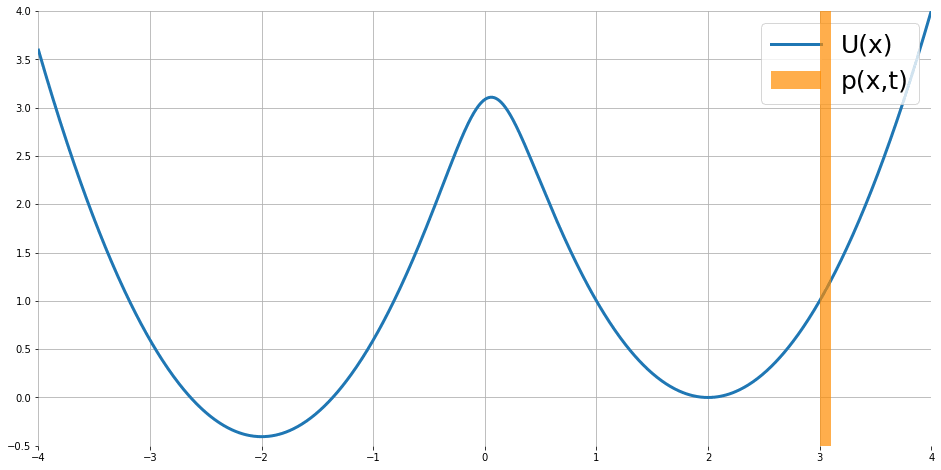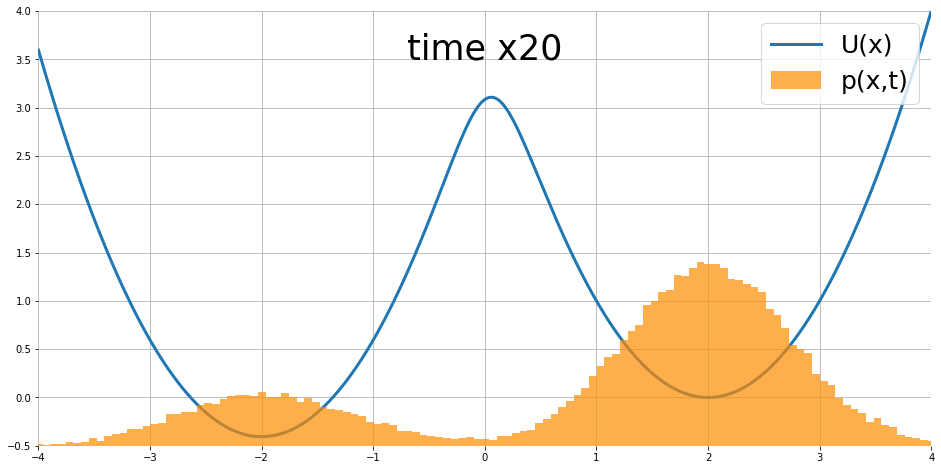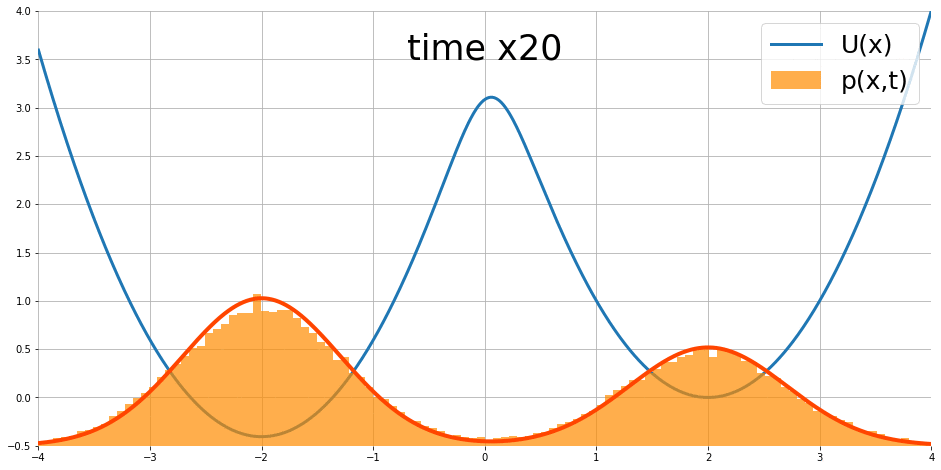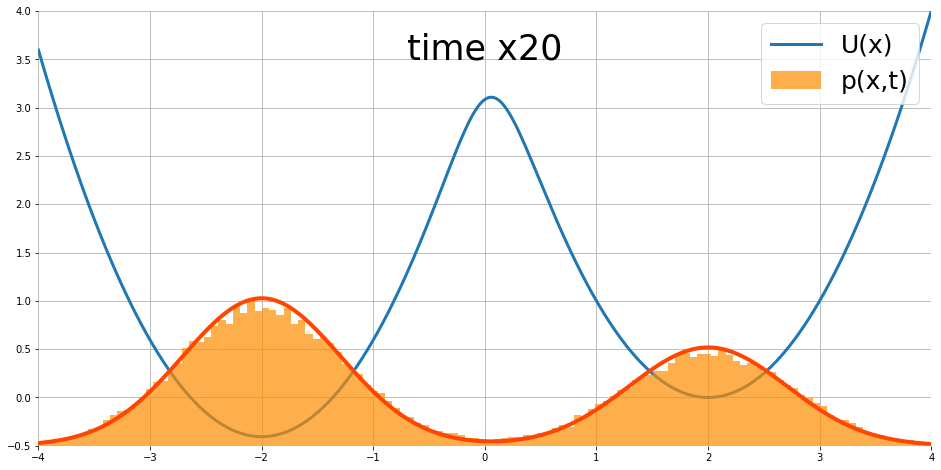
隨著時間似乎會達到 stationary distribution.
詳細推導請看最後一段 Appendix. 另外補充 F-P equation 與 Continuity equation 的關係可以參考論文的 Appendix D.
Stationary distribution
要怎麼找到這樣的 distribution? 流程就是先假設有 stationary density 且令其為 Gibbs distribution, $p_G(x)$, 的形式
$$p_G(x)=\frac{1}{Z}\exp\left(-\frac{U(x)}{T}\right)\\
,\text{where}\quad Z=\int\exp\left(-\frac{U(x)}{T}\right)dx$$ 然後帶入 Fokker-Planck equation 觀察什麼樣的情況會滿足.
我們最終得到 $T=\sigma^2/2$. 說明了 stationary distribution 的長相為 $T=\sigma^2/2$ 的 Gibbs distribution.
[$T=\sigma^2/2$ 的推導]
我們會利用到 divergence, $\nabla\cdot$, 具有 linearity 性質.
把 $p_G(x)$ 帶入到 Fokker-Planck equation 其中 normalization term $Z$ 可以忽略 (會被除掉)
$$0=\left(\nabla\exp(-U(x)/T)\right)^T\nabla U(x)+\exp(-U(x)/T)\nabla\cdot\nabla U(x)+\frac{1}{2}\sigma^2\nabla\cdot\nabla\exp(-U(x)/T) \\
= \nabla\cdot\left[\exp(-U(x)/T)\nabla U(x)\right]+\frac{1}{2}\sigma^2\nabla\cdot\nabla\exp(-U(x)/T) \\
=\nabla\cdot\left[\exp(-U(x)/T)\nabla U(x)-\frac{\sigma^2}{2T}\exp(-U(x)/T)\nabla U(x)\right] \\
=\nabla\cdot\left[\left(1-\frac{\sigma^2}{2T}\right)\exp(-U(x)/T)\nabla U(x)\right]=0$$ 注意到最後一行由於我們沒有對 potential field $U(x)$ 有所限制
因此 $=0$ 只有可能中括號內 $=0$, 所以
$$\left(1-\frac{\sigma^2}{2T}\right)\exp(-U(x)/T)\nabla U(x)=0 \\
\Longrightarrow 1-\frac{\sigma^2}{2T}=0 \Longrightarrow T=\frac{\sigma^2}{2}$$
對目標分布做採樣
因此我們知道, 如果使用 Langevin equation 做擴散的話且希望它最終達到 target distribution $p(x)$, 只要定義 $U(x)=-\log p(x)$ and $\sigma=\sqrt{2}$, i.e. $T=1$. 則根據 $p_G(x)$ 的定義, $p_G(x)$ 會等於我們的 target distribution $p(x)$, 又已知 $p_G(x)$ 為 stationary distribution, 所以用 Langevin equation 擴散隨著時間到最後等同於從 $p_G(x)=p(x)$ 採樣.
所以可以這麼做 Langevin dynamics sampling (只利用到 score function 做 sampling) (圖片來源) (圖片來源)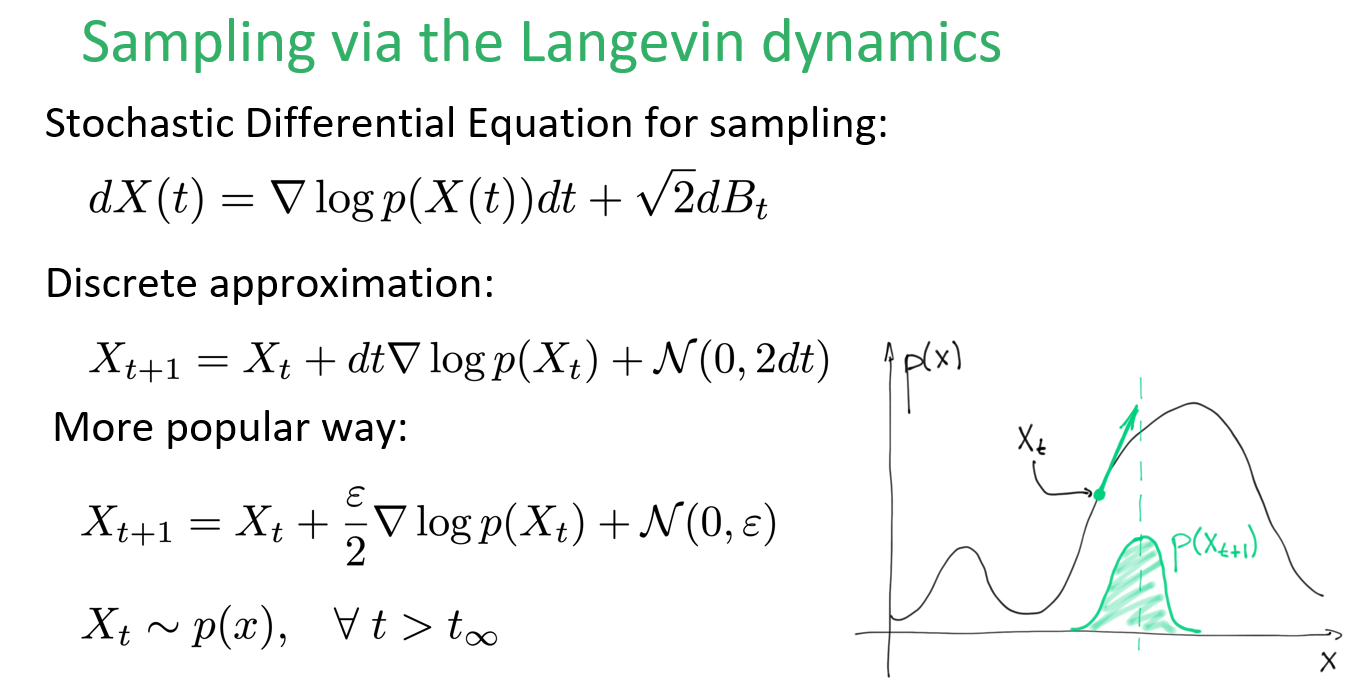
Appendix: Derivation of the Fokker-Planck Equation
重複一下 Langevin dynamics
$$dX(t)=-\nabla U(X(t))dt+\sigma dBt$$ 離散化:
$$\begin{align}
x-x'=-\nabla U(x')dt+\mathcal{N}(0,\sigma^2dt) \\
\Longrightarrow x\sim\mathcal{N}(x'-\nabla U(x')dt,\sigma^2dt):=q(x|x')
\end{align}$$ (圖片來源)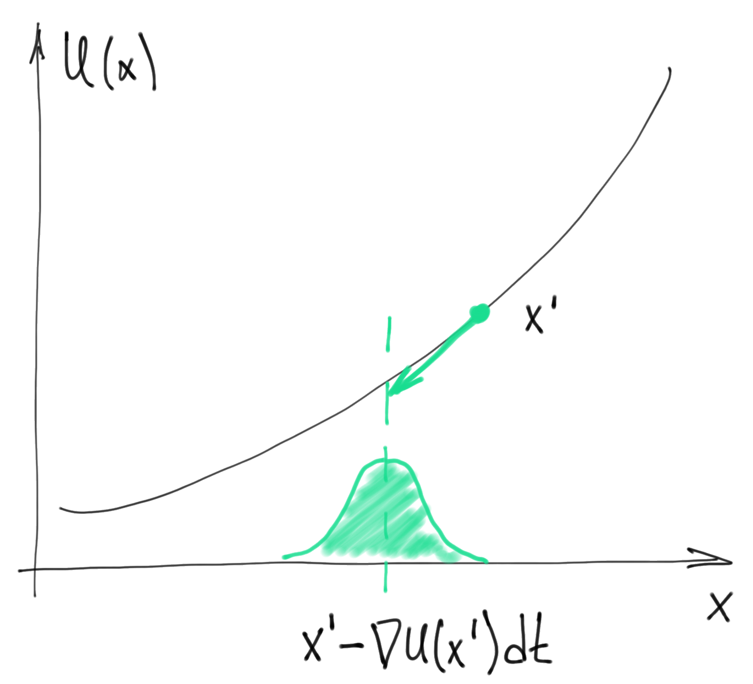
所以 $p_t(x)$ 我們可以這麼寫:
$$\begin{align}
p_t(x)=\int p_{t-dt}(x')q(x|x')dx'
\end{align}$$ 注意到 $p_{t-dt}(x')$ 我們也不知道. 但我們知道 $q(x|x’)$ 定義在式 (5), 展開來:
$$\begin{align}
q(x|x')=\frac{1}{(2\pi\sigma^2 dt)^{n/2}}\exp\left(\frac
{-({\color{orange}{x'-x-\nabla U(x')dt}})^2}
{2\sigma^2dt}\right) \\
\end{align}$$ 定義:
$$\begin{align}
{\color{orange}{y\triangleq x'-x-\nabla U(x')dt}}:=f(x')
\end{align}$$ 則根據 change of variables 我們知道式 (6) 變成
$$\begin{align}
p_t(x)=\int p_{t-dt}({\color{blue}{x'(y)}})\mathcal{N}(y|0,\sigma^2dt\cdot I)
{\color{blue}{\left|\frac{\partial x'}{\partial y}\right|}}
dy
\end{align}$$ 就算簡化了 $q(x|x’)$ 成上式, 藍色的部分 ${\color{blue}{x'(y)}}$, ${\color{blue}{|\partial x'/\partial y|}}$ 我們仍不知道, 必須想辦法從 $y$ (8) 的定義反寫.
先處理比較好做的 ${\color{blue}{|\partial x'/\partial y|}}$
根據定義 $y=x'-x-\nabla U(x')dt$ 且我們有 $(I-A)^{-1}=I+A+A^2+A^3+...$ 的公式 [ref], 先計算 $\partial y/\partial x'$ 得到:
$$\frac{\partial y}{\partial x'}=I-\text{div}\nabla U(x')dt:=I-Adt$$ 其中 $\text{div}$ 表示 divergence, 再計算 inverse:
$$\frac{\partial x'}{\partial y}=\left(\frac{\partial y}{\partial x'}\right)^{-1}=\left(I-Adt\right)^{-1} \\
=I+Adt+o(dt) \\
=I+\text{div}\nabla U(x')dt + o(dt)$$ 所以
$$\begin{align}
{\color{blue}{\left|\frac{\partial x'}{\partial y}\right|}}=1+\text{div}\nabla U(x')dt+o(dt)
\end{align}$$ 再想辦法把 ${\color{blue}{x'(y)}}$ 寫出來, 比較複雜, 把 $\nabla U(x’)$ 在 $x$ 這點做 Taylor expansion:
$$y\triangleq x'-x-\nabla U(x')dt \\
= x'-x-\left(
\nabla U(x)+(x'-x)\frac{\partial \nabla U(x)}{\partial x}+o(x'-x)
\right)dt \\$$ 把 $x’$ 合併展開並整理, 並注意到因為根據 (4), $o(x’-x)dt$ 這項為 $o(dt)$, 繼續推導:
$$=\left(I-\frac{\partial \nabla U(x)}{\partial x}dt\right)x'-x -\nabla U(x)dt +x\frac{\partial \nabla U(x)}{\partial x}dt + o(dt) \\
\Longrightarrow x'=\left(I-\frac{\partial \nabla U(x)}{\partial x}dt\right)^{-1}
\left(y+x+\nabla U(x)dt-x\frac{\partial \nabla U(x)}{\partial x}dt+o(dt)
\right)$$ 利用 $(I-A)^{-1}=I+A+A^2+A^3+...$ 的公式 [YouTube with time] [ref]:
$$\left(I-\frac{\partial \nabla U(x)}{\partial x}dt\right)^{-1}=I+\frac{\partial \nabla U(x)}{\partial x}dt+o(dt)$$ 代回去得到
$$x'=\left(I+\frac{\partial \nabla U(x)}{\partial x}dt+o(dt)\right)
\left(y+x+\nabla U(x)dt-\frac{\partial \nabla U(x)}{\partial x}xdt+o(dt)
\right) \\
=y+x+\nabla U(x)dt-\frac{\partial \nabla U(x)}{\partial x}xdt+\frac{\partial \nabla U(x)}{\partial x}ydt+\frac{\partial \nabla U(x)}{\partial x}xdt+o(dt) \\
=y+x+\nabla U(x)dt+\frac{\partial \nabla U(x)}{\partial x}{\color{orange}{ydt}}+o(dt)$$ 先對 $ydt$ 分析一下到時候代回去
根據 $y$ 和 $x-x’$ 的定義 (8) 和 (4):
$$y= x'-x-\nabla U(x')dt \\
= \nabla U(x')dt-\mathcal{N}(0,\sigma^2dt)-\nabla U(x')dt \\
=-\mathcal{N}(0,\sigma^2dt)$$ 所以
$$ydt=-\mathcal{N}(0,\sigma^2dt)dt=-dt\sqrt{dt}\mathcal{N}(0,\sigma^2) \\
=o(dt)$$ 代回去得到
$$\begin{align}
x'=y+x+\nabla U(x)dt+\frac{\partial \nabla U(x)}{\partial x}{\color{orange}{o(dt)}}+o(dt) \\
\Longrightarrow {\color{blue}{x'(y)}}=x+y+\nabla U(x)dt+o(dt)
\end{align}$$ 因此 (10), (12) 代回去 (9)
$$\begin{align}
p_t(x)=\int p_{t-dt}({\color{blue}{x'(y)}})\mathcal{N}(y|0,\sigma^2dt\cdot I)
{\color{blue}{\left|\frac{\partial x'}{\partial y}\right|}}
dy \\
= (1+\text{div}\nabla U(x)dt)\mathbb{E}_y\left[
{\color{red}{p_{t-dt}(x+y+\nabla U(x)dt)}}
\right] \\
,\quad\text{where}\quad y\sim\mathcal{N}(0,\sigma^2dt\cdot I)
\end{align}$$ 紅色部分做 Taylor expansion 對 $p_t(x)$ 展開:
(0th order): $p_t(x)$
(1st order):
$$\nabla p_t(x)^T(y+\nabla U(x)dt) + \frac{\partial }{\partial t}p_t(x)(-dt)$$ (2nd order):
$$\frac{1}{2}(y+\nabla U(x)dt)^T\frac{\partial^2p_t(x)}{\partial x^2}(y+\nabla U(x)dt)$$ 2nd order 還有對 $t$ 的二次微分項, $(dt)^2(\partial^2 p_t(x)/\partial t^2)$ 由於是 $o(dt)$ 所以可以省略不寫
取 $\mathbb{E}_y$:
(0th order): 與 $y$ 無關, 是 constant:
$$\mathbb{E}_y[p_t(x)]=p_t(x)$$
(1st order):
$$\mathbb{E}_y\left[\nabla p_t(x)^T(y+\nabla U(x)dt) + \frac{\partial }{\partial t}p_t(x)(-dt)\right] \\
=\nabla p_t(x)^T(\mathbb{E}_y[y]+\nabla U(x)dt)-\frac{\partial }{\partial t}p_t(x)dt \\
=\nabla p_t(x)^T\nabla U(x)dt-\frac{\partial }{\partial t}p_t(x)dt$$ (2nd order):
$$\frac{1}{2}\mathbb{E}_y\left[(y+\nabla U(x)dt)^T\frac{\partial^2p_t(x)}{\partial x^2}(y+\nabla U(x)dt)\right] \\
=\frac{1}{2}\mathbb{E}_y\left[
y^t\frac{\partial^2p_t(x)}{\partial x^2}y\right] + 2dt\nabla U(x)^T\frac{\partial^2p_t(x)}{\partial x^2}\mathbb{E}_y[y] + o(dt) \\
= \frac{1}{2}\mathbb{E}_y\left[
y^t\frac{\partial^2p_t(x)}{\partial x^2}y\right] + o(dt) \\
=\frac{1}{2}\sum_{i=j}\left(\frac{\partial^2p_t(x)}{\partial x^2}\right)_{ii}\mathbb{E}_y[y_i^2] + \frac{1}{2}\sum_{i\neq j}\left(\frac{\partial^2p_t(x)}{\partial x^2}\right)_{ij}\mathbb{E}_y[y_iy_j] + o(dt) \\$$ 因為 $y\sim\mathcal{N}(0,\sigma^2dt\cdot I)$, see (7) and (8), 所以第二項為零
$$=\frac{1}{2}\sum_{i=j}\left(\frac{\partial^2p_t(x)}{\partial x^2}\right)_{ii}\mathbb{E}_y[y_i^2] + o(dt) \\
= \frac{1}{2}\sum_{i=j}\left(\frac{\partial^2p_t(x)}{\partial x^2}\right)_{ii}\sigma^2dt + o(dt) \\
= \frac{1}{2}\nabla^2p_t(x)\sigma^2dt + o(dt)$$ 其中 $\nabla^2$ 是 Laplace operator.
因此代回去 (14):
$$p_t(x)= (1+\text{div}\nabla U(x)dt)\mathbb{E}_y\left[
p_{t-dt}(x+y+\nabla U(x)dt)
\right] \\
\approx (1+\text{div}\nabla U(x)dt) \\ \cdot \left(
p_t(x)+\nabla p_t(x)^T\nabla U(x)dt-\frac{\partial }{\partial t}p_t(x)dt+\frac{1}{2}\nabla^2p_t(x)\sigma^2dt + o(dt)
\right)$$ 展開整理得
$$\frac{\partial }{\partial t}p_t(x)=\nabla p_t(x)^T\nabla U(x)+p_t(x)\text{div}\nabla U(x)+\frac{1}{2}\sigma^2\nabla^2p_t(x)+\underbrace{\frac{o(dt)}{dt}}_{=0}$$ 重複一次, 這就是最後的 Fokker-Planck equation:
$$\frac{\partial }{\partial t}p_t(x)=\nabla p_t(x)^T\nabla U(x)+p_t(x)\text{div}\nabla U(x)+\frac{1}{2}\sigma^2\nabla^2p_t(x)$$ Q.E.D.