Stochastic Gradient Descent (SGD) 算法:
$$\begin{align*} \quad w_{k+1}=w_k-\alpha_k\nabla_wf(w_k,x_k) \end{align*}$$ 其中 $f$ 是要 minimized 的目標函數, $x_k$, $w_k$ 是 $k$-th iteration 的 data 和 weight.以前在學的時候都會提到 step size $\alpha_k$ 有這樣一個神奇的條件:
$$\sum_{k=1}^\infty \alpha_k^2<\infty,\quad \sum_{k=1}^\infty \alpha_k=\infty;$$ 左邊的條件希望 step size 要愈來愈小, 而右邊的條件又說也不能太小.
聽起來就有點神奇, 不知道藏了什麼秘密在裡面.
直到許多年後, 在我學赵世钰老師的 RL 課程第 6 章的時候才解開了以前不懂的地方.
鄭重介紹 Robbins-Monro (RM) 算法!
RM 可說十分重要, 除了可以證明 SGD 是 RM 算法的一個 special case. (因此只要保證滿足 RM 收斂的條件, SGD 就會收斂)
同時 RL (強化學習) 裡經典的 Temporal Difference (TD), Q-Learning 等的方法也依賴 RM 算法的觀念.
所以 RM 算法可說是 RL 的基石之一! 知道 RM 算法還是相當有好處的.
以下特別筆記赵世钰老師的 RL 課程第 6 章 內容.
Robbins-Monro Algorithm and Theorem
一句話描述 RM 算法可以解什麼問題: 在不知道函式長相且觀測值具有誤差情況下, 解 root finding problem
(當然有一些前提條件要滿足)
具體來說我們要找 $w$ s.t. $g(w)=0$, 但我們只能觀測到有誤差的值 $\tilde{g}(w,\eta)=g(w)+\eta$: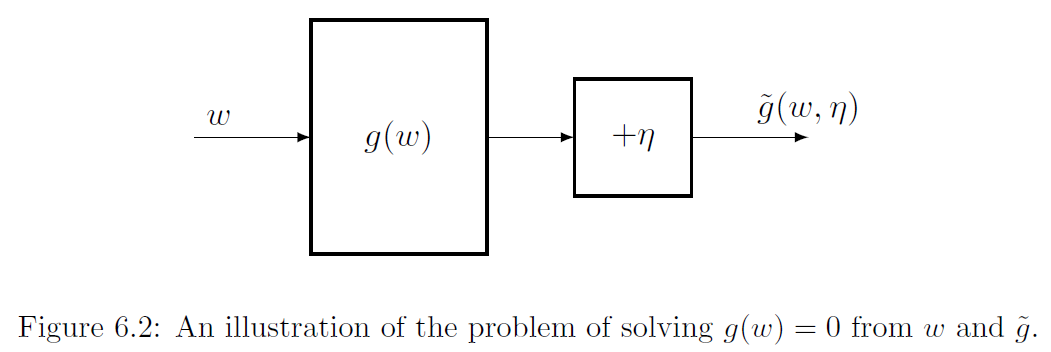
(這個誤差 random variable $\eta$ 是精髓)
由於很多時候 $g(w)$ 會是真實期望值, 但由於我們只能觀測到有誤差的 sample 值
這種觀測 sample 與真實期望值之間的差, 就是 random variable $\eta$, 因此就能套進 RM 算法框架中.
SGD 和 RL 中的 TD, Q-Learning 就是這麼套用的.
Robbins-Monro Algorithm
RM 算法流程為:
$$\begin{align}
{\color{orange}{w_{k+1}=w_k-a_k\tilde{g}(w_k,\eta_k)}},\quad k=1,2,3,...
\end{align}$$ 其中 $a_k\geq 0$ 且有一些條件要滿足, $\eta_k$ 是觀測 noise 也同樣有一些條件要滿足, 見下面 RM theorem
Robbins-Monro Theorem
對 RM algorithm (1) 來說, 如果滿足:
1. $0\leq c_1\leq\nabla_wg(w)\leq c_2,\quad \forall w;$ (函式 $g$ 為單調遞增)
2. $\sum_{k=1}^\infty a_k=\infty$ and $\sum_{k=1}^\infty a_k^2<\infty;$
3. $\mathbb{E}[\eta_k|\mathcal{H}_k]=0$ and $\mathbb{E}[\eta_k^2|\mathcal{H}_k]<\infty;$
其中 $\mathcal{H}_k=\{w_k,w_{k-1},...\}$ 表示過往的紀錄 (稱 filtration)
則 $w_k$ almost surely (a.s.) converges 到 root $w^\ast$, where $g(w^\ast)=0$.
分析:
- 第 1 個條件在最佳化問題 (optimize 函式 $f(w)$) 的時候, 由於我們設定 $g(w)=\nabla_w f(w)$ 所以變成要求 $\nabla_w^2 f(w)$ 必須是正定矩陣, 即 $f$ 是 strictly convex function.
- 第 2 個條件很有趣, 首先如果滿足 $\sum_{k=1}^\infty a_k^2<\infty$, 表示 $a_k\longrightarrow 0$ for $k\longrightarrow\infty$ (反證法即可知), 說明希望 $a_k$ 確實要愈來愈小, 這位什麼重要呢? 我們分析一下
因為 $w_{k+1}-w_k=-a_k\tilde{g}(w_k,\eta_k)$, 如果 $\tilde{g}$ is bounded 則
$$\because a_k\xrightarrow[k\rightarrow\infty]{} 0, \quad \therefore a_k\tilde{g}\xrightarrow[k\rightarrow\infty]{} 0;\quad\Longrightarrow (w_{k+1}-w_k)\xrightarrow[k\rightarrow\infty]{} 0$$ 不然的話 $w_{k+1}-w_k$ 會震盪.
再來 $\sum_{k=1}^\infty a_k=\infty$ 則希望 $a_k$ 不要過小, 這樣有什麼好處呢? 我們觀察 (1)
$$\begin{align*} (1)\Longrightarrow w_{k+1}-w_k=-a_k\tilde{g}(w_k,\eta_k) \\ \Longrightarrow\sum_{k=1}^\infty(w_{k+1}-w_k)=-\sum_{k=1}^\infty a_k\tilde{g}(w_k,\eta_k) \\ \Longrightarrow w_\infty-w_1=-\sum_{k=1}^\infty a_k\tilde{g}(w_k,\eta_k) \end{align*}$$ 如果 $\sum_{k=1}^\infty a_k<\infty$ 加上 $\tilde g$ 是 bounded, 則 $w_\infty-w_1<\infty$ 是 bounded, 這樣會讓我們的 initial $w_1$ 沒辦法隨意選擇 - 第 3 個條件, 一般來說 $\{\eta_k\}$ 是 i.i.d. 滿足 $\mathbb{E}[\eta_k]=0$ 和 $\mathbb{E}[\eta_k^2]<\infty$
RM theorem 的證明要使用下段介紹的 Dvoretzky’s convergence theorem
Dvoretzky’s Convergence Theorem
考慮如下的 stochastic process
$$\begin{align}
{\color{orange}{\Delta_{k+1}=(1-\alpha_k)\Delta_k+\beta_k\eta_k}}, \quad k=1,2,3,...
\end{align}$$ 其中 $\{\alpha_k\}_{k=1}^\infty$, $\{\beta_k\}_{k=1}^\infty$, 和 $\{\eta_k\}_{k=1}^\infty$ 也都是 stochastic sequences, 且 $\alpha_k\geq0,\beta_k\geq0$ for all $k$. 則
$$\Delta_k\xrightarrow[]{a.s.}0,\quad k\rightarrow\infty$$ 如果滿足以下條件:
1. $\sum_{k=1}^\infty \alpha_k=\infty$, $\sum_{k=1}^\infty \alpha_k^2<\infty$, and $\sum_{k=1}^\infty \beta_k^2<\infty$ uniformly almost surely;
2. $\mathbb{E}[\eta_k|\mathcal{H}_k]=0$ and $\mathbb{E}[\eta_k^2|\mathcal{H}_k]\leq C;$
其中 $\mathcal{H}_k=\{\Delta_k,\Delta_{k-1},..., \eta_{k-1},...,\alpha_{k-1},...,\beta_{k-1},...\}$ 表示過往的紀錄 (稱 filtration).
證明請自行看課本: Book-Mathematical-Foundation-of-Reinforcement-Learning, [3 - Chapter 6 Stochastic Approximation.pdf]
用 Dvoretzky’s Convergence Theorem 證明 Robbins-Monro Theorem
令 $w^\ast$ 為 root, i.e. $g(w^\ast)=0$. 改寫一下 RM algo. (1)
$$\begin{align*}
w_{k+1}=w_k-a_k(g(w_k)+\eta_k) \\
\Longrightarrow w_{k+1}-w^\ast=w_k-w^\ast-a_k( {\color{green}{g(w_k)-g(w^\ast)}} +\eta_k)
\end{align*}$$ 綠色的地方使用 mean value theorem, 即 $g(w_k)-g(w^\ast)=\nabla_w g(w_k')(w_k-w^\ast)$, 並令 $\Delta_k=w_k-w^\ast$ 代回去得到:
$$\begin{align*}
\Longrightarrow \Delta_{k+1}=\Delta_k-a_k(\nabla_w g(w_k')\Delta_k+\eta_k) \\
\Longrightarrow \Delta_{k+1}=(1-\underbrace{a_k\nabla_w g(w_k')}_{\doteq\alpha_k})\Delta_k + \underbrace{a_k}_{\doteq\beta_k} (-\eta_k)
\end{align*}$$ 很容易看到從 RM thoerem 要求的條件能滿足 Dvoretzky’s convergence theorem 的要求條件, 因此 $\Delta_k\longrightarrow0$, as $k\longrightarrow\infty$.
即 $w_k\longrightarrow w^\ast$, as $k\longrightarrow\infty$.
SGD 是 RM Algorithm 的一個特例
首先我們有 Loss function 如下:
$$\min_w J(w)=\frac{1}{n}\sum_{i=1}^nf(w,x_i)=\mathbb{E}[f(w,X)]$$ Gradient Descent (GD) 和 SGD 算法如下:
$$\begin{align*}
\text{GD:}\quad w_{k+1}
=w_k-\alpha_k\mathbb{E}[\nabla_wf(w_k,X)]\\
\text{SGD}:\quad w_{k+1}=w_k-\alpha_k\nabla_wf(w_k,x_k)
\end{align*}$$ GD 計算 gradient 的時候要對所有的 data 計算後取期望, 而 SGD 只取一個 sample 的 gradient.
定義 $g(w)$:
$$g(w)\doteq\mathbb{E}[\nabla_wf(w,X)]$$ 則當 $w^\ast$ 為 root 時, 滿足 $g(w^\ast)=0\Longrightarrow \mathbb{E}[\nabla_wf(w,X)]=0$, gradient 為 0 表示達到 critical point. (解了最佳化問題)
而真正觀測值為 SGD 的 gradient:
$$\tilde{g}(w)=\nabla_wf(w,x)=g(w)+\underbrace{[\nabla_wf(w,x)-\mathbb{E}[\nabla_wf(w,X)]]}_{\doteq \eta}$$ 套用 RM 算法可以發現正好是 SGD 算法:
$$\begin{align*}
\text{RM algo}\quad w_{k+1}=w_k-\alpha_k\tilde{g}(w_k,\eta_k) \\
\text{SGD algo}\quad=w_k-\alpha_k\nabla_wf(w,x)
\end{align*}$$ 因此 RM 算法的收斂性和條件可以直接延伸過去給 SGD.