Convolution 與 BatchNorm 的融合大法：從推論、QAT 到 PyTorch 的加速

發表於 | 分類於 | [object Object]

常見的 NN blocks: Convolution (Conv) —> Batch Normalization (BN) —> ReLU
這 3 個 OPs 在量化後 inference 的時候可以直接融合成一個 OP:
  - Conv —> BN 可以融合是因為 BN 可以視為一個 1x1 convolution, 所以兩者的 weights 可以合併
  - ReLU 可以合併是因為在 QAT 時, 可以被 fake quant 的 quantization parameter 處理掉

本文筆記 Conv+BN 的合併, 分 3 部分:
  - 先討論 inference 階段怎麼合併 (已經都 train 好的情況下) [來源]
  - 再來討論做 QAT 時, 怎麼插 fake quant 效果才會好 [來源]
  - 最後看看 PyTorch 怎麼實作, 更重要的是, 怎麼加速?

Inference 階段融合 Conv+BN

這段筆記來源: https://nenadmarkus.com/p/fusing-batchnorm-and-conv/
回顧一下, 給定一個 minibatch $(N,C,H,W)$, BN 對 $(N,H,W)$ 做 normalization: [圖來源]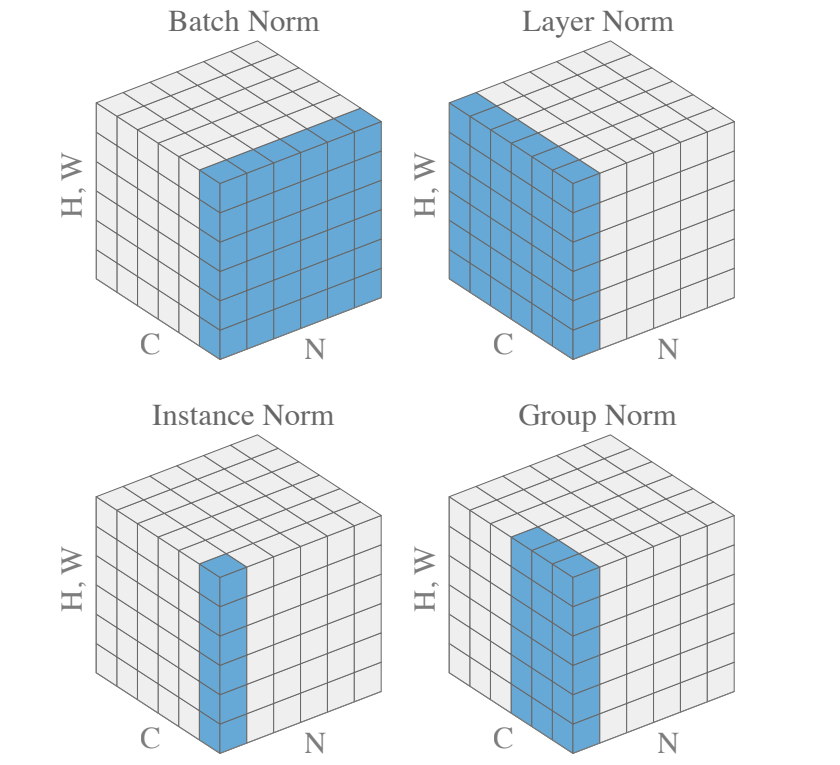

也就是對每一個 channel $c$ 計算出 mean $\mu_c$ 和 standard deviation $\sigma_c$:

例如 input tensor x_in = torch.randn(n, c, h, w) , mu_c = torch.einsum('nchw->c', x_in) / (n * h * w)
所以 mu_c.shape == c.

對 batch 裡每一筆 feature map $x=(C,H,W)$, BN 對每一個 $c\in[1,C]$ 作如下的 normalization:
$$\hat{x}_c=\gamma\frac{x_c-\mu_c}{\sigma_c}+\beta$$ 其中 $\gamma,\beta$ 是 BN 的參數, 學出來的. 另外通常為了數值穩定不會直接除 $\sigma_c$, 而是會除 $\sigma_c+\epsilon$.
這個操作可以寫成一個 1x1 conv:
$$\begin{align} \left[\begin{array}{c} \hat{x}_{1,i,j}\\\hat{x}_{2,i,j}\\\vdots\\\hat{x}_{C-1,i,j} \\\hat{x}_{C,i,j} \end{array}\right] = \underbrace{ \left[\begin{array}{ccccc} \frac{\gamma_1}{\sigma_1} & 0 & \cdots & & 0 \\ 0 & \frac{\gamma_2}{\sigma_2} & & & \\ \vdots & & \ddots & & \vdots \\ & & & \frac{\gamma_{C-1}}{\sigma_{C-1}} & 0 \\ 0 & \cdots & & & \frac{\gamma_C}{\sigma_C} \\ \end{array}\right] }_{W_{bn}} \left[\begin{array}{c} x_{1,i,j} \\ x_{2,i,j} \\ \vdots \\ x_{C-1,i,j} \\ x_{C,i,j} \end{array}\right] + \underbrace{ \left[\begin{array}{c} \beta_1-\gamma_1\frac{\mu_1}{\sigma_1} \\ \beta_2-\gamma_2\frac{\mu_2}{\sigma_2} \\ \vdots \\ \beta_{C-1}-\gamma_{C-1}\frac{\mu_{C-1}}{\sigma_{C-1}} \\ \beta_C-\gamma_C\frac{\mu_C}{\sigma_C} \end{array}\right] }_{b_{bn}} \end{align}$$ 其中 $W_{bn}\in\mathbb{R}^{C\times C}$, $b_{bn}\in\mathbb{R}^{C\times 1}$.
我們假設前一層 kernel size $k\times k$ 的 convolution 參數為 $W_{conv}\in\mathbb{R}^{C\times(C_{prev}\cdot k^2)}$, $b_{conv}\in\mathbb{R}^{C\times 1}$, $C_{prev}$ 表示 convolution 的 input channel
對 input feature map $\mathbf{f}_{i,j}$ 來說, 根據 convolution 做法的定義, 知道 $\mathbf{f}_{i,j}\in\mathbb{R}^{(C_{prev}\cdot k^2)\times1}$,
則 Conv—>BN:
$$\begin{align*} \hat{\mathbf{f}}_{i,j}=W_{bn}\cdot(W_{conv}\cdot\mathbf{f}_{i,j}+b_{conv})+b_{bn} \\ \Longrightarrow \hat{\mathbf{f}}_{i,j}=(W_{bn}\cdot W_{conv})\cdot\mathbf{f}_{i,j} + (W_{bn}\cdot b_{conv} + b_{bn}) \end{align*}$$ 所以合併後的 weight and bias:
$$\begin{align} W_{fused}=W_{bn}\cdot W_{conv} \\ b_{fused}=W_{bn}\cdot b_{conv} + b_{bn} \end{align}$$ 改寫一下:
$$\begin{align} W_{fused}=\frac{\gamma W_{conv}}{\sigma} \\ b_{fused}=\frac{\gamma b_{conv}}{\sigma}+\beta-\frac{\gamma\mu}{\sigma}=\beta-\gamma\frac{\mu-b_{conv}}{\sigma} \end{align}$$ Python exmple codes 可參考來源

QAT 對 Conv+BN 插 Fake-quant

這段筆記來自於論文 “Quantizing deep convolutional networks for efficient inference: A whitepaper” [arxiv], 圖為還原論文內容只是我重新畫而以.
觀察 (3), 可以發現如果 convolution 的 bias 為 0, 融合後仍有 bias 項 (由 BN 提供), 所以在 Conv+BN 情況下, Conv 可以不用設定 bias.
因此以下討論的 Conv 只有 weight 沒有 bias. 對 (4), (5) 重新命名改寫:
$$\begin{align} W_{train}=\frac{\gamma W}{\sigma_B}, \quad b_{train}=\beta-\gamma\frac{\mu_B}{\sigma_B} \\ W_{inf}=\frac{\gamma W}{\sigma}, \quad b_{inf}=\beta-\gamma\frac{\mu}{\sigma} \end{align}$$ 其中 $\mu_B,\sigma_B$ 為針對一個 batch 統計出來的 mean 和 std (training用的), 而 $\mu,\sigma$ 則是他們的 EMA, 即 exponential moving average (inference 用的).
$W$ 直接就是 Conv 的 weight, $W_{train},W_{inf}$ 分別表示 training 和 inference 時的 fused weight, 同理 $b_{train},b_{inf}$.

Baseline 插 fake-quant

分開看 training 和 inference 怎麼插 fake quant.

[Inference] (下圖左):
假設參數都已經訓練好了, 我們直接使用 (7) 融合 Conv 和 BN 得到 $W_{inf}$ 和 $b_{inf}$ 並插 fake quant 即可. (當然真正 inference 要再轉 integer)
注意到 inference 使用的是 EMA 的 $\mu$ 和 $\sigma$.

[Training] QAT(下圖右):
由於 BN 訓練的時候要使用 batch 的 $\mu_B$ 和 $\sigma_B$, 因此相比於 inference 時多了要計算 $\mu_B$ 和 $\sigma_B$ 的運算. 看下圖右可以發現, 多了一次 convolution 只為了得到 $\mu_B$ 和 $\sigma_B$.
然後使用 (6) 得到 $W_{train}$ 和 $b_{train}$.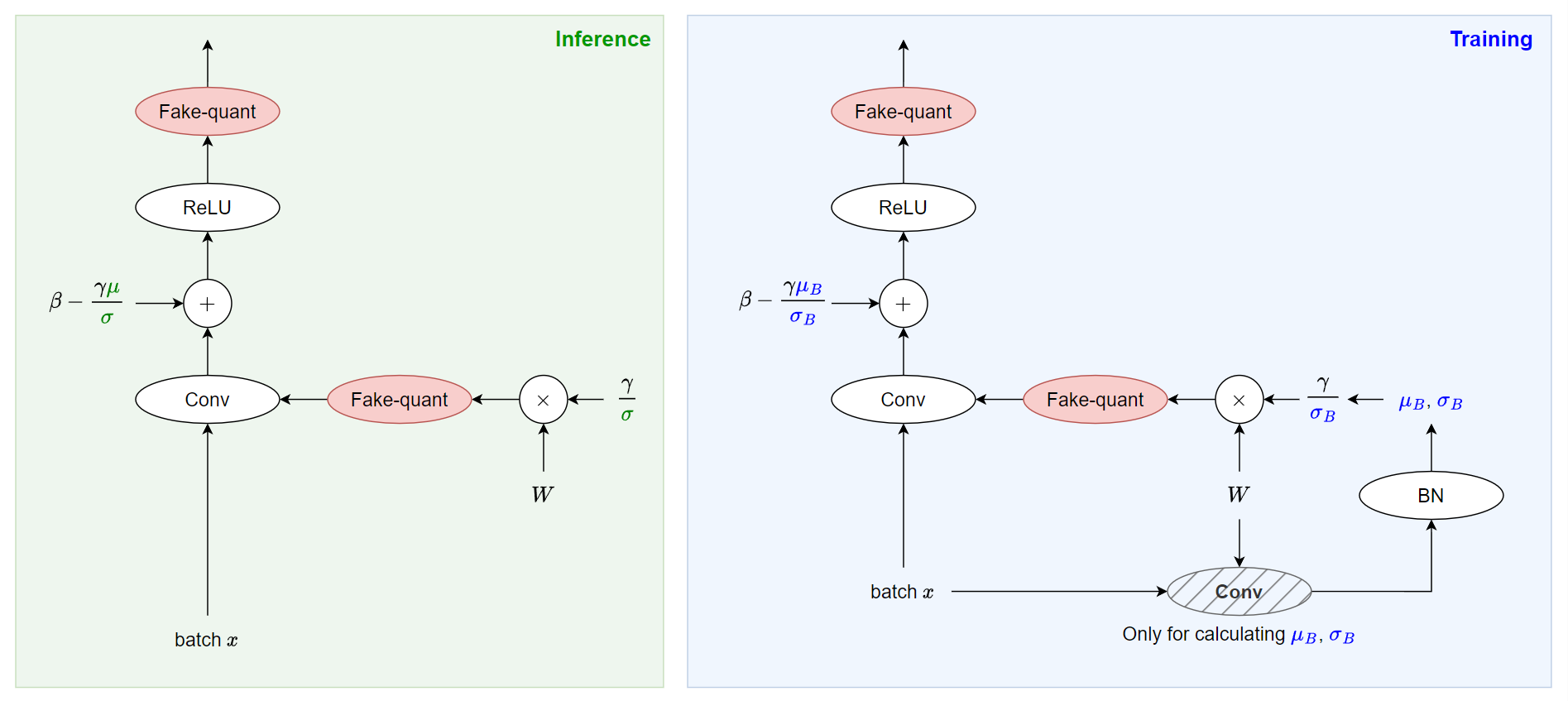

但是注意到, 這麼做 QAT 效果不好
因為 $\mu_B,\sigma_B$ 是針對一個 batch 去統計出來的本身就會變化劇烈, 如果再加上 fake quant 的 error (含 STE 的 gradient error) 會讓整個訓練很不穩定
論文實驗顯示 training loss 有 jitter 現象 (見下圖綠色 curve), 更詳細見論文的 Fig14 and 15.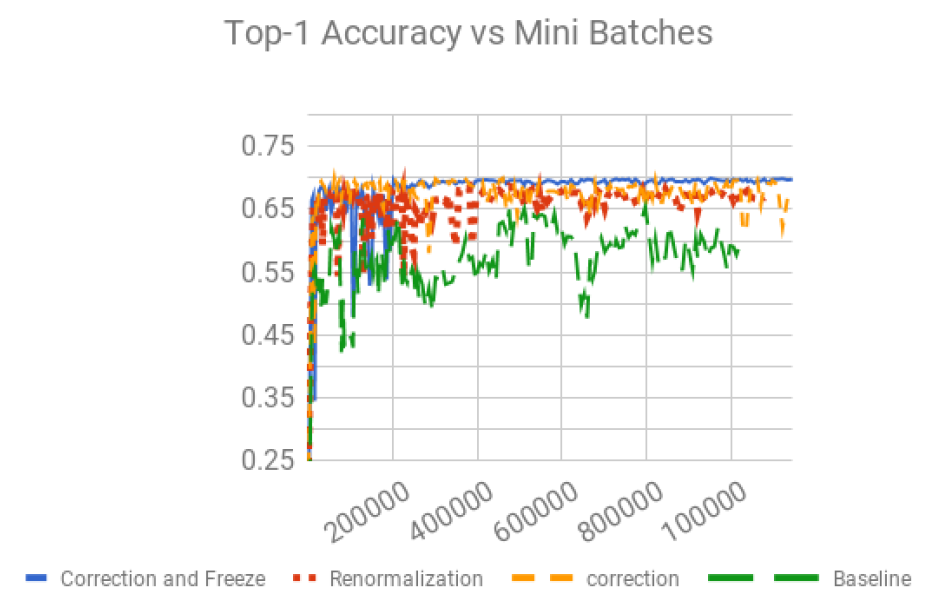

但如果 training 時使用 EMA $\mu,\sigma$ 這又不對, 會失去 BN 的效果.
所以這就面臨了兩難. 因此論文一個重要的貢獻就是解決此問題.

Fake Quant With Correction Term

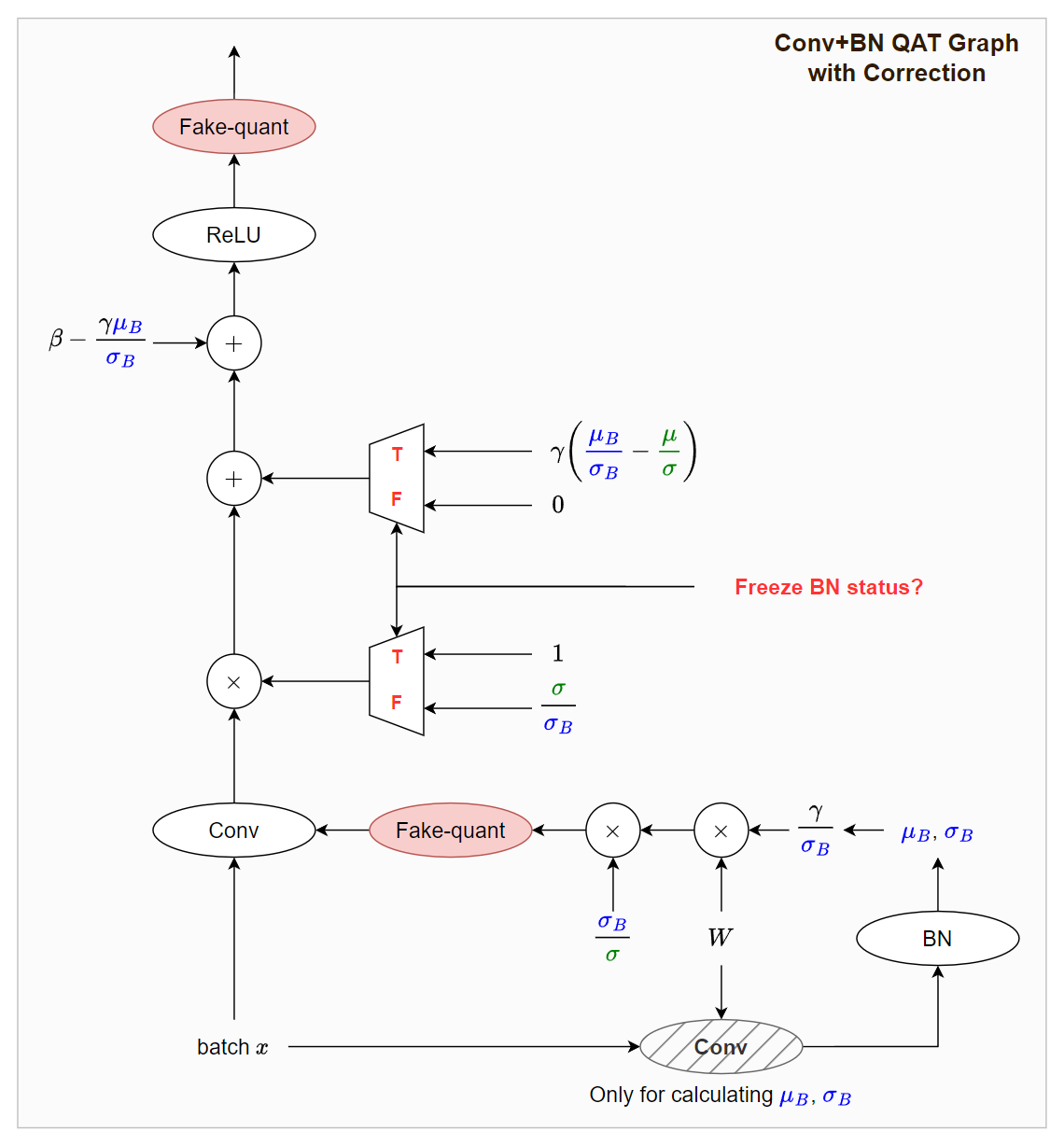
[Training]:
最大的改動就是對 $W$ 做 fake quant $fq(\cdot)$ 的時候使用的是 $W_{inf}$, 這樣就能避免上面提到的訓練不穩定現象 (jitter). 看上圖能知道:
$$fq\left(\frac{\sigma_B}{\sigma}\cdot W\cdot \frac{\gamma}{\sigma_B}\right) = fq\left(\frac{\gamma W} {\sigma}\right) = fq(W_{inf})$$ 但是我們希望 training 的時候仍然使用 $W_{train}$ (即使用 batch 的統計結果 $\mu_B,\sigma_B$ ), 所以乘上一個 correction term $\sigma/\sigma_B$ 還原, 意思是:
$$\begin{align*} \frac{\sigma}{\sigma_B}\cdot fq(W_{inf})\approx fq\left(\frac{\sigma}{\sigma_B}\cdot\frac{\gamma W} {\sigma}\right) \\ =fq\left(\frac{\gamma W}{\sigma_B}\right)=fq(W_{train}) \end{align*}$$ 這樣我們就能在 training 的時候就能使用 $W_{train}$, 且又能避免 fake quant 造成的不穩定.
觀察一下 bias term, 注意到此時不能 freeze BN status 所以圖中的邏輯閘為 False:
$$0 + \beta - \frac{\gamma\mu_B}{\sigma_B} = \beta-\frac{\mu_B}{\sigma_B} = b_{train}$$

[Inference]:
此時要 freeze BN status 所以邏輯閘為 True
因此不用乘上 correction term $\sigma/\sigma_B$, 所以用的是 $W_{inf}$ 去做 fake quant.
觀察一下 bias term, 設定邏輯閘為 True:
$$\gamma\left(\frac{\mu_B}{\sigma_B}-\frac{\mu}{\sigma}\right) + \beta - \frac{\gamma\mu_B}{\sigma_B} = \beta-\frac{\mu}{\sigma} = b_{inf}$$

PyTorch 作法

上面提到的作法 “fake quant with correction term” 就是 PyTorch _ConvBnNd 這個 class 的 _forward_slow 作法 [code link]
名字上都有 slow 這個字眼了, 但為什麼是 slow 呢?
其實我們上面有提過, 為了計算一個 batch 的 $\mu_B$ 和 $\sigma_B$ 要多一次 convolution 運算.
PyTorch 做了 _forward_approximate [code link] 來加速, 但注意到如同函數名字一樣, 雖然加速, 但這是 approximate 作法. (也是預設做法)
我們來分析看看 PyTorch 怎麼避掉那個多的 covolution 吧…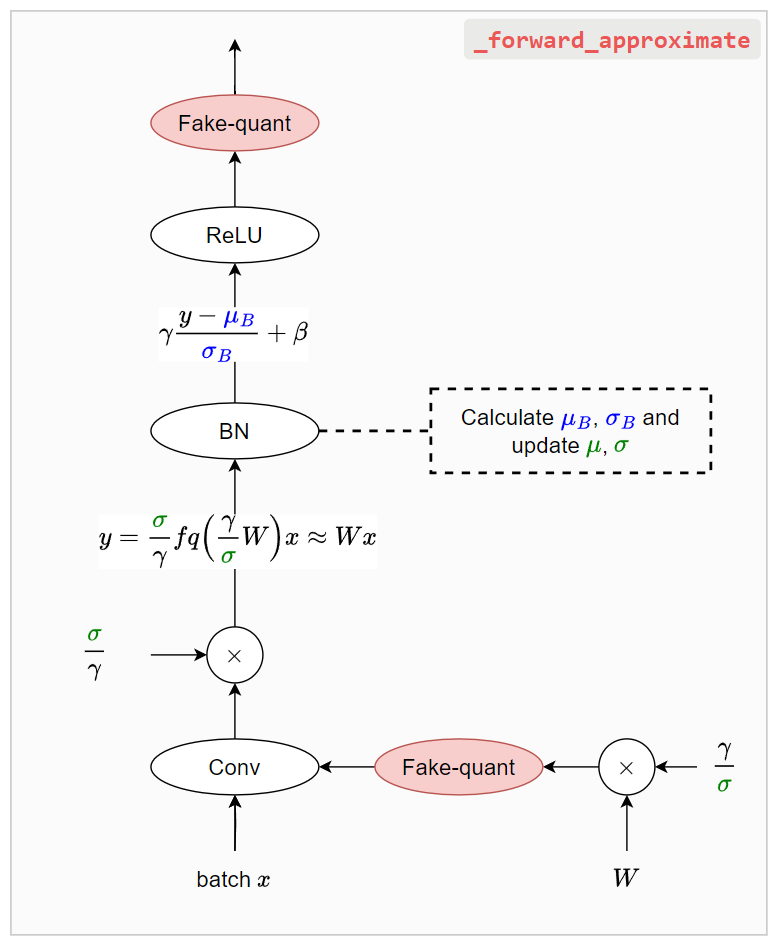

跟論文做法 (_forward_slow) 最主要差別是在套用 BN 的時候, $\mu_B$ 和 $\sigma_B$ 的統計是已經經過 fake quant 後的值去統計出來的
注意到原本論文作法, $\mu_B$ 和 $\sigma_B$ 使用的是最精準的 float 結果 (無 fake quant 損失) 去統計的.

8-bit quantize 經驗上做這樣的 approximate 影響不大, 或許在 lower bit rate, e.g. <4-bits, 情況下才可能要注意?!

雖然是 approximate 作法, 但少了一次 convolution 運算就快不少.
對應的 PyTorch 官方實作:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def _forward_approximate(self, input):
        """Approximated method to fuse conv and bn. It requires only one forward pass.
        conv_orig = conv / scale_factor where scale_factor = bn.weight / running_std
        """
        assert self.bn.running_var is not None
        running_std = torch.sqrt(self.bn.running_var + self.bn.eps)
        scale_factor = self.bn.weight / running_std
        weight_shape = [1] * len(self.weight.shape)
        weight_shape[0] = -1
        bias_shape = [1] * len(self.weight.shape)
        bias_shape[1] = -1
        scaled_weight = self.weight_fake_quant(
            self.weight * scale_factor.reshape(weight_shape)
        )
        # using zero bias here since the bias for original conv
        # will be added later
        if self.bias is not None:
            zero_bias = torch.zeros_like(self.bias, dtype=input.dtype)
        else:
            zero_bias = torch.zeros(
                self.out_channels, device=scaled_weight.device, dtype=input.dtype
            )
        conv = self._conv_forward(input, scaled_weight, zero_bias)
        conv_orig = conv / scale_factor.reshape(bias_shape)
        if self.bias is not None:
            conv_orig = conv_orig + self.bias.reshape(bias_shape)
        conv = self.bn(conv_orig)
        return conv

Summary

總結來說幾個要點:

  • 對 convolution weight $W$ 做 fake quant 的時候要採用 EMA mean/std $\mu,\sigma$.
  • QAT 訓練的時候, 給 ReLU 的 input activation 仍然要使用 $\mu_B,\sigma_B$, 這是因為 BN 訓練時就是根據 batch 去計算的
  • PyTorch 實作了 _forward_approximat 藉此避掉因為要統計最精確的 $\mu_B,\sigma_B$ 而多出來的一個 convolution 運算, 雖然加快, 但代價是稍微不精確 (8-bit quant 經驗上還好, 但更低的 quant 可能會有影響)

References

  1. Fusing batch normalization and convolution in runtime [blog]
  2. Quantizing deep convolutional networks for efficient inference: A whitepaper [arxiv]
  3. Pytorch _forward_approximate and _forward_slow (in torch.ao.nn.intrinsic.qat.modules.conv_fused.py)

本文圖檔文件: ConvBN_fusion.drawio