某天忘記幹嘛了突然回想起之前學到的一個問題是有關 gradient 的 variance 很大, 使得 gradient descent 訓練不夠穩定.
不過可以利用扣掉一個 bias 或是使用 re-parameterization trick 來大幅降低 variance 解決此問題.
想了很久忘了在哪邊…縱使翻自己的 blog 筆記有時也沒查到很全面的資訊.
所以就開始跟 ChatGPT 學習, 只能說 👏🏻 ChatGPT 完美!! 👏🏻
現在這個時代隨時都有一個上通天文下知地理的助手在你旁邊 (或許無法贏過專精該領域最頂尖的人類, 但作為輔助絕對稱得上稱職), 這在以前根本很難想像, 且也只是這短短幾年才發生的事情.
這麼棒的東西, 還不把它用爆嗎?
好了, 回到本篇文章, 以下除了開頭的問題設定, 以及有一段人工補充的段落, 其他都是 ChatGPT 寫的, 根本超方便.
問題設定
假設我們有一個機率分佈 $p_\theta(x)$,其中 $x$ 是隨機變數,而 $\theta$ 是控制該分佈的參數。我們的目標是對以下期望值求梯度:
$$F(\theta)=\mathbb{E}_{x\sim p_\theta}[f(x)]$$ 即:
$$F(\theta) = \int f(x) p_\theta(x) dx$$ 我們希望計算 $\nabla_\theta F(\theta)$。
推導 REINFORCE Estimator
直接對積分求梯度:
$$\nabla_\theta F(\theta) = \nabla_\theta \int f(x) p_\theta(x) dx$$ 為 $p_\theta(x)$ 是依賴於 $\theta$ 的,我們使用 log-derivative trick,即:
$$\nabla_\theta p_\theta(x) = p_\theta(x) \nabla_\theta \log p_\theta(x)$$ 將其帶入上式:
$$\begin{align*}
\nabla_\theta F(\theta) = \int f(x) \nabla_\theta p_\theta(x) dx \\
= \int f(x) p_\theta(x) \nabla_\theta \log p_\theta(x) dx \\
= \mathbb{E}_{x \sim p_\theta} [f(x) \nabla_\theta \log p_\theta(x)]
\end{align*}$$ 這就是 REINFORCE estimator:
$$\nabla_\theta F(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} f(x_i) \nabla_\theta \log p_\theta(x_i)$$ 其中 $x_i \sim p_\theta(x)$ 是從該分佈中抽樣的樣本。
直覺解釋
關鍵技巧是對機率密度取對數的梯度:
$$\nabla_\theta p_\theta(x) = p_\theta(x) \nabla_\theta \log p_\theta(x)$$ 這使得我們可以用機率本身作為權重,而不直接對機率密度求梯度(避免計算困難)。這是一種無偏估計 (unbiased estimator):
$$\mathbb{E}_{x \sim p_\theta} [f(x) \nabla_\theta \log p_\theta(x)]$$ 這個估計的期望值與真實梯度一致。只需要能對樣本計算對數機率的梯度:
- 這使得該方法適用於各種離散或連續分佈。
應用
這個技巧非常普遍,除了 Reinforcement Learning 之外,也應用於:
- 變分推理 (Variational Inference):用來估計變分下界 (ELBO) 的梯度。
- 黑箱優化 (Black-box optimization):在不知道目標函數明確梯度的情況下仍可進行參數更新。
- 離散隨機變數的梯度估計:適用於沒有可微分重參數化技巧 (reparameterization trick) 的情境。
這樣的推導完全基於機率分佈的性質,並不依賴於強化學習的框架。
改善 REINFORCE Estimator 的方法
REINFORCE estimator 雖然是一種無偏 (unbiased) 估計方法,但它的主要問題是 方差過大 ,導致學習不穩定。以下是一些常見的改善方法:
基線 (Baseline) 方法
由於 REINFORCE estimator 的梯度公式是:
$$\nabla_\theta F(\theta) = \mathbb{E}_{x \sim p_\theta} [f(x) \nabla_\theta \log p_\theta(x)]$$ 如果我們從中減去某個與 $x$ 無關的基線 $b$,梯度估計仍然是無偏的:
$$\nabla_\theta F(\theta) = \mathbb{E}_{x \sim p_\theta} [(f(x) - b) \nabla_\theta \log p_\theta(x)]$$ 因為 $\mathbb{E}[\nabla_\theta \log p_\theta(x)] = 0$,所以加入 $b$ 不影響期望值,但可以降低方差。
[推導]:
從機率分佈的性質出發,對任何參數 $\theta$ 控制的機率密度 $p_\theta(x)$,我們知道它的總機率必須滿足歸一化條件:
$$\int p_\theta(x) dx = 1$$ 對兩邊對 $\theta$ 求梯度:
$$\nabla_\theta \int p_\theta(x) dx = \int \nabla_\theta p_\theta(x) dx = 0$$ 接著,我們應用 log-derivative trick(即 score function 的概念):
$$\nabla_\theta p_\theta(x) = p_\theta(x) \nabla_\theta \log p_\theta(x)$$ 將這個代入上式:
$$\int p_\theta(x) \nabla_\theta \log p_\theta(x) dx = 0$$ 這其實就是期望值的定義:
$$\mathbb{E}_{x \sim p_\theta} [\nabla_\theta \log p_\theta(x)] = 0$$ 這證明了對於任何機率分佈 $p_\theta(x)$,它的 log 機率的梯度的期望值總是 $0$。
[直覺]:
當 $f(x)$ 本身有高方差時,減去一個適當的基線可以讓梯度的變化更小,使優化更穩定。
常見選擇:
- 均值基線: $$b = \mathbb{E}[f(x)]$$
- 狀態價值函數:$b=V(x)$,這就是 Actor-Critic 方法中的 Critic 作用。
控制變數 (Control Variates)
這種方法是基於 方差減少技術 (variance reduction techniques),可以通過添加一個與梯度相關但均值為 0 的項來減少方差。例如:
$$\nabla_\theta F(\theta) = \mathbb{E}_{x \sim p_\theta} [(f(x) - c(x)) \nabla_\theta \log p_\theta(x)]$$ 其中 $c(x)$ 是一個選擇得當的函數,使得 新梯度估計的方差較低。
[應用]:
- 一種常見的選擇是讓 $c(x)$ 盡量貼近 $f(x)$ 的趨勢,這樣可以減少變異性。
- 在強化學習中,這可以是 優勢函數 $A(s,a)$,這就是 Advantage Actor-Critic (A2C/A3C) 方法的基礎。
[使用 Control Variates 估計 KL divergence]
此段為人工補充, 參考自 [YouTube]
當要估計兩個 distributions $P(x)$ and $Q(x)$ 的時候通常使用 KL-divergence 當作”距離”衡量
注意到因為非對稱所以嚴格上非距離定義
所以 $D_{KL}(P\|Q)$ 和 $D_{KL}(Q\|P)$ 分別對應 mode averaging 和 mode seeking 兩種行為 [YouTube with time stamp]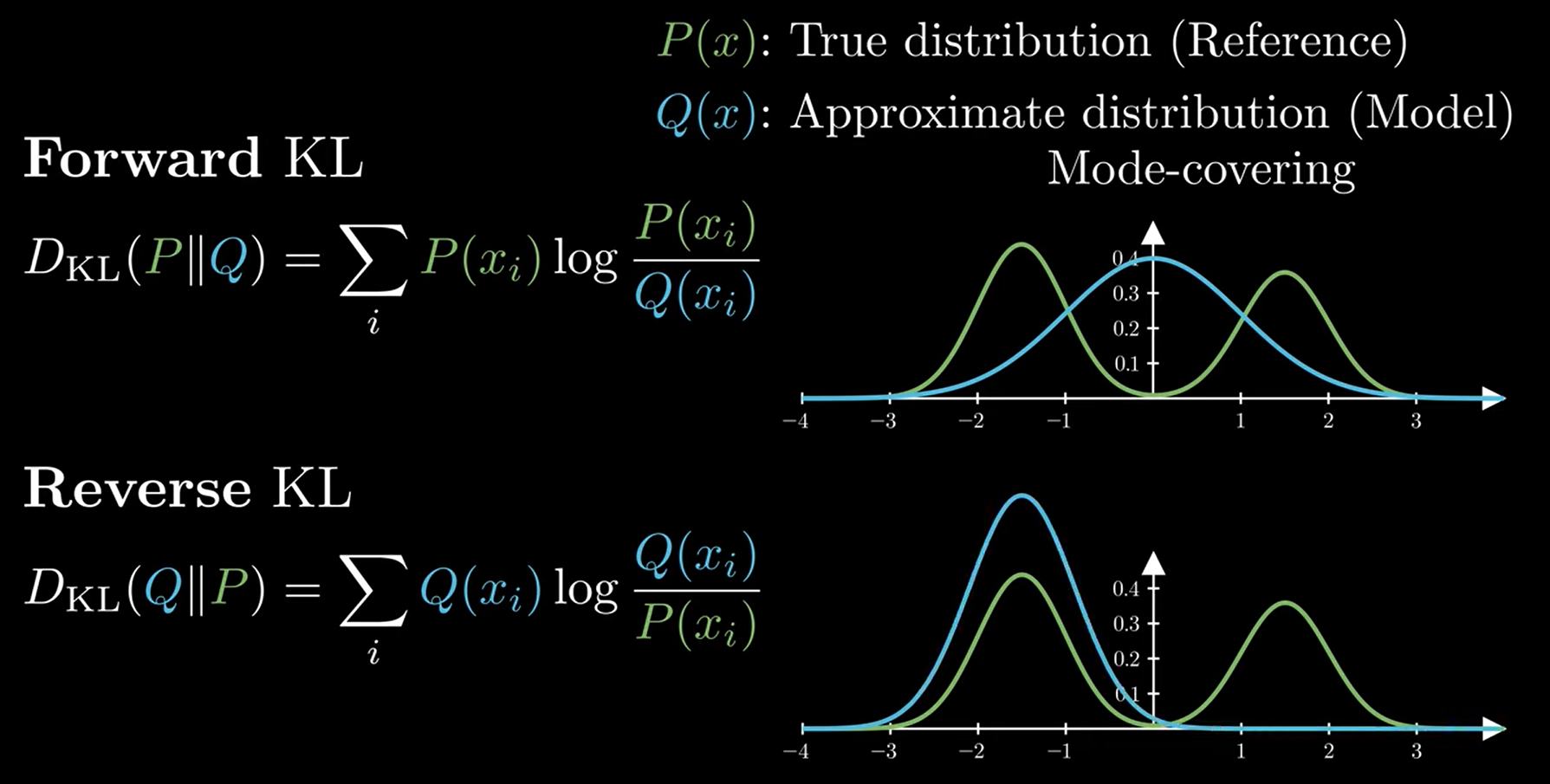
扯遠了, 回到 KL-div 估計
首先 KL-div 的 Monte Carlo 估計為:
$$\begin{align*}
D_{KL}(P\|Q)=\mathbb{E}_{x\sim P}\left[\log\frac{P(x)}{Q(x)}\right] \\
\approx \frac{1}{N}\sum_{k=1}^N\log\frac{P(x_k)}{Q(x_k)},\quad\text{where }x_k\sim P
\end{align*}$$ 則將 $c(x)$ 定義為, 其中 $\lambda$ 是個常數 (之後會設定為 $1$)
$$\begin{align*}
c(x)\doteq -\lambda(r(x)-\mathbb{E}_{x\sim P}\left[r(x)\right])
\end{align*}$$ 很容易驗證 $\mathbb{E}_{x\sim P}[c(x)]=0$
那麼我們得到 KL-div MC 的 control variates 版本:
$$\begin{align*}
\hat{D}_{KL}(P\|Q)=\frac{1}{N}\sum_{k=1}^N\left[
\log\frac{P(x_k)}{Q(x_k)} - c(x_k)
\right] \\
=\frac{1}{N}\sum_{k=1}^N\left[
\log\frac{P(x_k)}{Q(x_k)} + \lambda(r(x_k)-\mathbb{E}_{x\sim P}\left[r(x_k)\right])
\right]
\end{align*}$$ 最後定義 $r(x)=Q(x)/P(x)$, 則我們知道 $\mathbb{E}_{x\sim P}[r(x)]=1$.
代入上式變成:
$$\begin{align*}
\hat{D}_{KL}(P\|Q)=\frac{1}{N}\sum_{k=1}^N\left[
-\log r(x_k) + \lambda(r(x_k)-1)
\right]
\end{align*}$$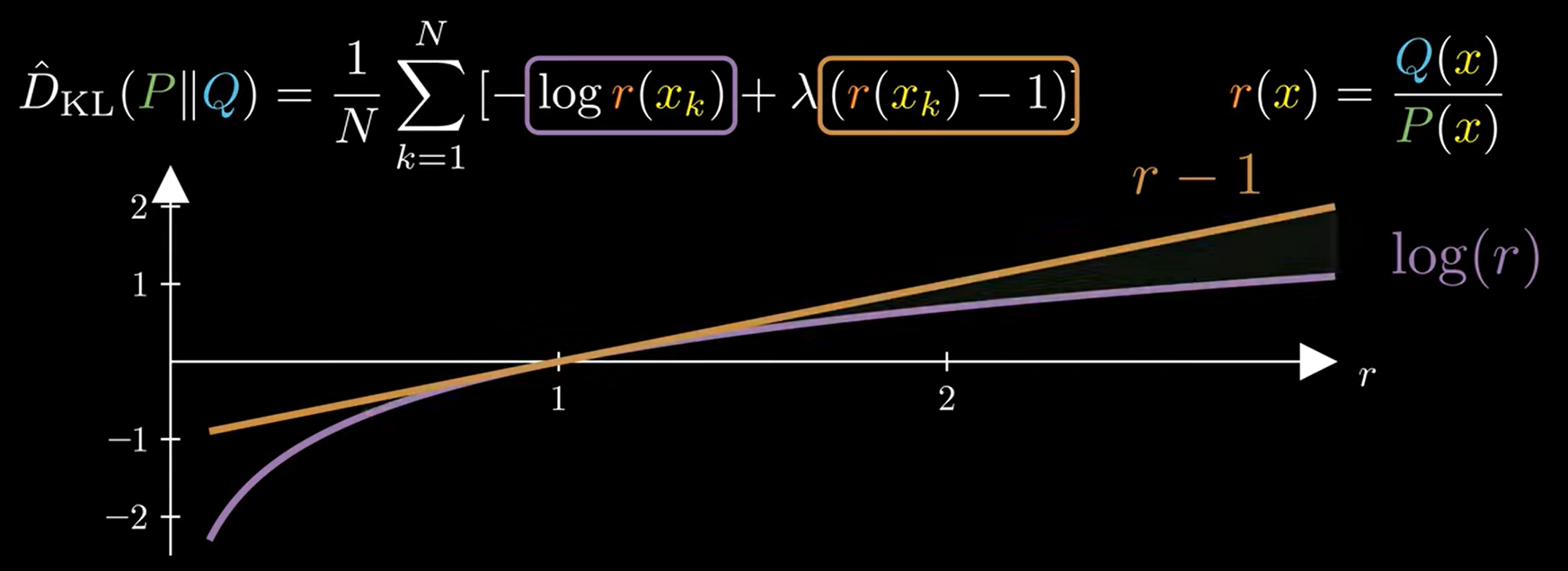
可以發現當 $\lambda=1$ 的時候, 橘色減去紫色一定 $>0$. 所以保證了 $\hat{D}_{KL}(P\|Q)\geq0$. (這很好, 因為本來 KL-div 就是 non-negative)
所以我們得到了 unbias 且 low variance 的 KL-divergence 估計方法了! Great 👏🏻!
低方差梯度估計 (Low-Variance Gradient Estimators)
當我們的分佈 $p_\theta(x)$ 是連續的時,通常可以用 重參數化技巧 (Reparameterization Trick) 來減少梯度估計的方差。
[概念]:
如果我們可以將 $x$ 重新參數化為一個可微的變換,即:
$$x = g(\epsilon, \theta)$$ 其中 $\epsilon$ 是與 $\theta$ 無關的隨機變數,那麼期望可以改寫為:
$$\mathbb{E}_{x \sim p_\theta} [f(x)] = \mathbb{E}_{\epsilon \sim p(\epsilon)} [f(g(\epsilon, \theta))]$$ 這樣求梯度時:
$$\nabla_\theta F(\theta) = \mathbb{E}_{\epsilon \sim p(\epsilon)} [\nabla_\theta f(g(\epsilon, \theta))]$$ 這種方式的梯度方差通常遠小於 REINFORCE estimator。
[應用]:
- 高斯分佈 $x \sim \mathcal{N}(\mu, \sigma^2)$ 時,可以重參數化為:
$$x = \mu + \sigma \epsilon, \quad \epsilon \sim \mathcal{N}(0,1)$$ 這就是變分自動編碼器 (VAE) 使用的技巧。 - 但這方法不適用於離散隨機變數,因此在離散情境下仍需使用 REINFORCE 或其他變異性降低技巧。
使用 Natural Gradient (自然梯度)
REINFORCE 使用標準的梯度下降方法,但有時可以透過 自然梯度 (Natural Gradient) 改善收斂速度。自然梯度的公式是:
$$\tilde{\nabla}_\theta = F^{-1} \nabla_\theta J(\theta)$$ 其中 $F$ 是 Fisher 信息矩陣 (Fisher Information Matrix),它考慮了參數空間的幾何性質,使梯度下降的步伐更合理。
[應用]:
- 自然梯度方法在 Trust Region Policy Optimization (TRPO) 和 Natural Policy Gradient (NPG) 中被使用,這些方法比普通梯度下降更穩定。
總結
| 方法 | 主要目標 | 主要技術 |
|---|---|---|
| 基線 (Baseline) | 減少方差 | 減去一個不影響期望的基線 $b$ |
| 控制變數 (Control Variates) | 減少方差 | 選擇適當的函數 $c(x)$ 來減少變異性 |
| 重參數化技巧 (Reparameterization Trick) | 降低梯度估計方差 | 透過變換將梯度計算從概率分佈轉換為函數內部計算 |
| 自然梯度 (Natural Gradient) | 提高學習效率 | 使用 Fisher 信息矩陣來進行更新 |
不同方法適用於不同情境,通常可以組合使用,例如:
- Actor-Critic = Baseline + Advantage Control Variates
- Variational Autoencoder (VAE) = Reparameterization Trick
- TRPO = Natural Gradient + Trust Region Constraint
這些技術的目標都是讓梯度估計更穩定、更高效。