我們在看一些 attention 有時會看到會將 key 和 value ($K,V$) 各自 padding 一個 zero vector 的 token embedding. 如下圖所示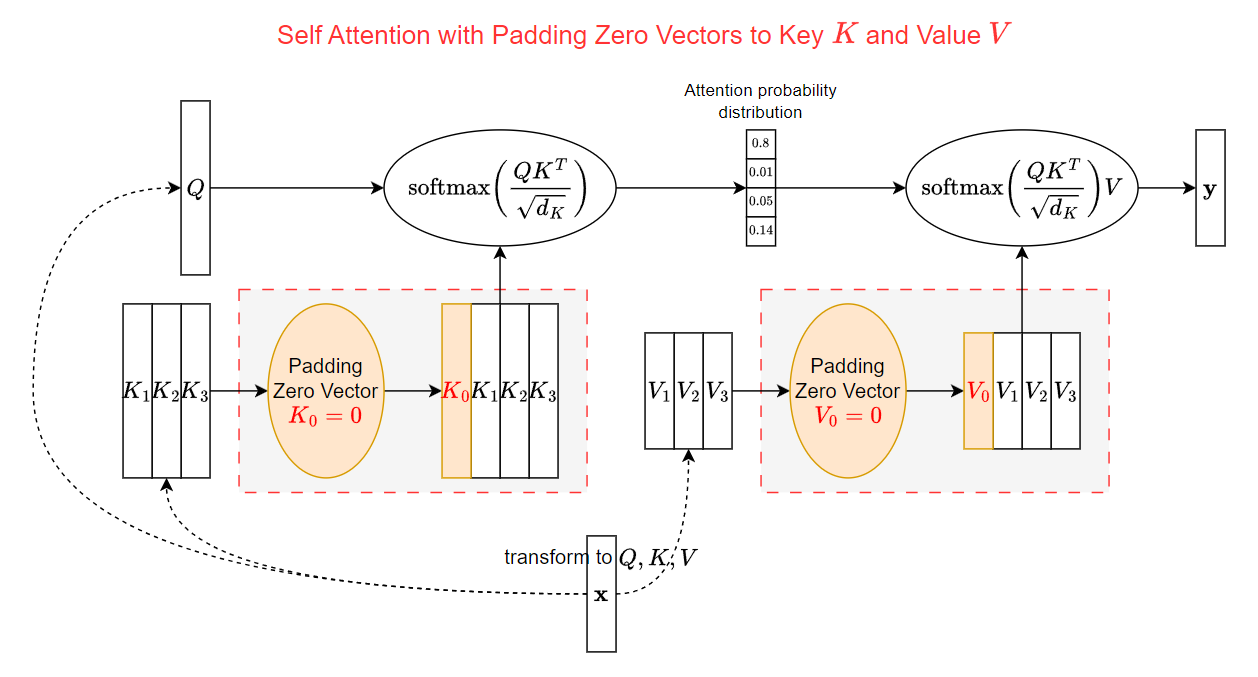 
初次看到可能會很疑惑, 為啥要多 padding zero vectors? 本文就來解釋一下原因.
但首先故事要先回到 Transformer 本身
以下一些投影片內容取自 Song Han 課程投影片
Transformer 的消耗改善
眾所周知 Transformer 的 attention 計算消耗為 $O(T^2)$ 其中 $T$ 為 context (token) length
而雖然 KV-cache memory 消耗為 $O(T)$ 但 out token 長度稍大的話記憶體需求很容易直接超過 model 本身的大小了
基於此理由, 減少 context length 對計算或記憶體的影響就很關鍵
縮短 Attention 的 Context Length
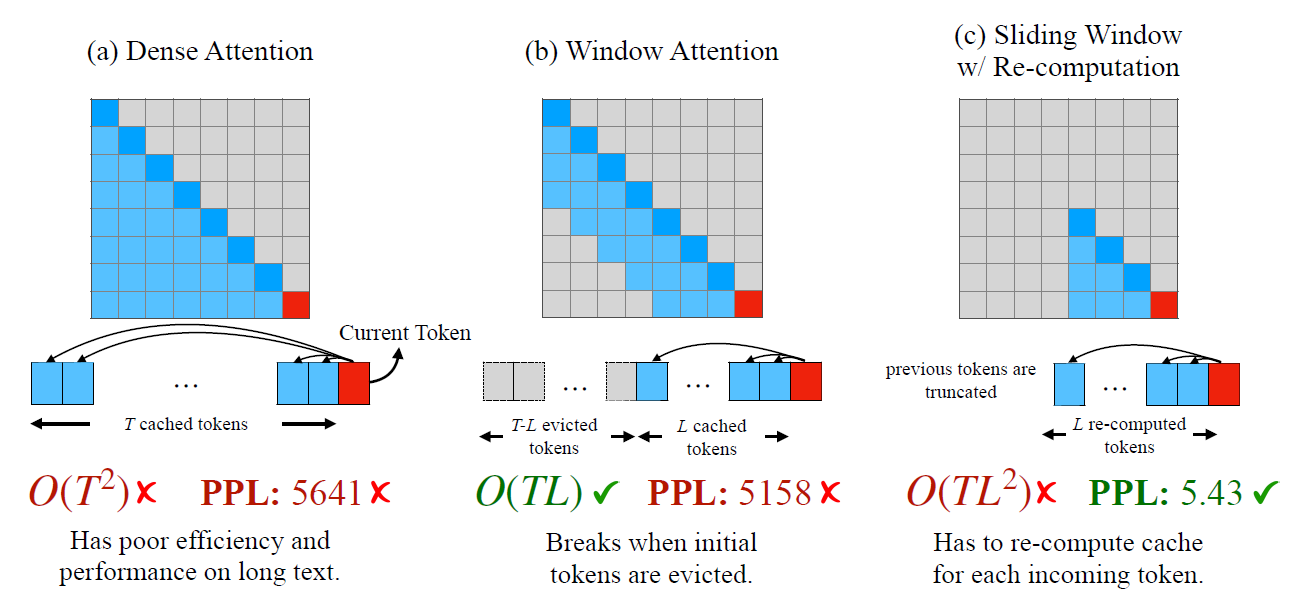Dense attention (a) 是原本的結果, 可以看到如果 inference 的時候 context length 超過 training 當時設定的長度時, 則 PPL 就爆掉了. 不僅如此計算開銷非常大 $O(T^2)$.
一個很直覺的改善方法就是讓 attention 只能處理過去的 $L$ 個 (含自己) tokens, 這樣計算開銷就變成固定值, $O(TL)$. 這方法稱為 window attention (b).
但是一旦要輸出超過第 $L$ 個位置的 token 的話, PPL 一樣馬上爆掉.
為了改善這現象, (c) sliding window w/ re-computation 方法就乾脆設定每 $L$ 個 tokens 後就 reset 整個 Transformer, 意思是一樣是做 dense attetion, 只是每 $L$ 個 tokens 後就 reset.
這方法雖然 PPL 沒問題了, 但是計算量仍然算高 $O(TL^2)$.
有沒有更好的方法讓計算量低的同時 PPL 也不會爆掉呢?
有的, 但提出方法之前要先理解到底 window attention (b) 為什麼會壞掉
The “Attention Sink” Phenomenon
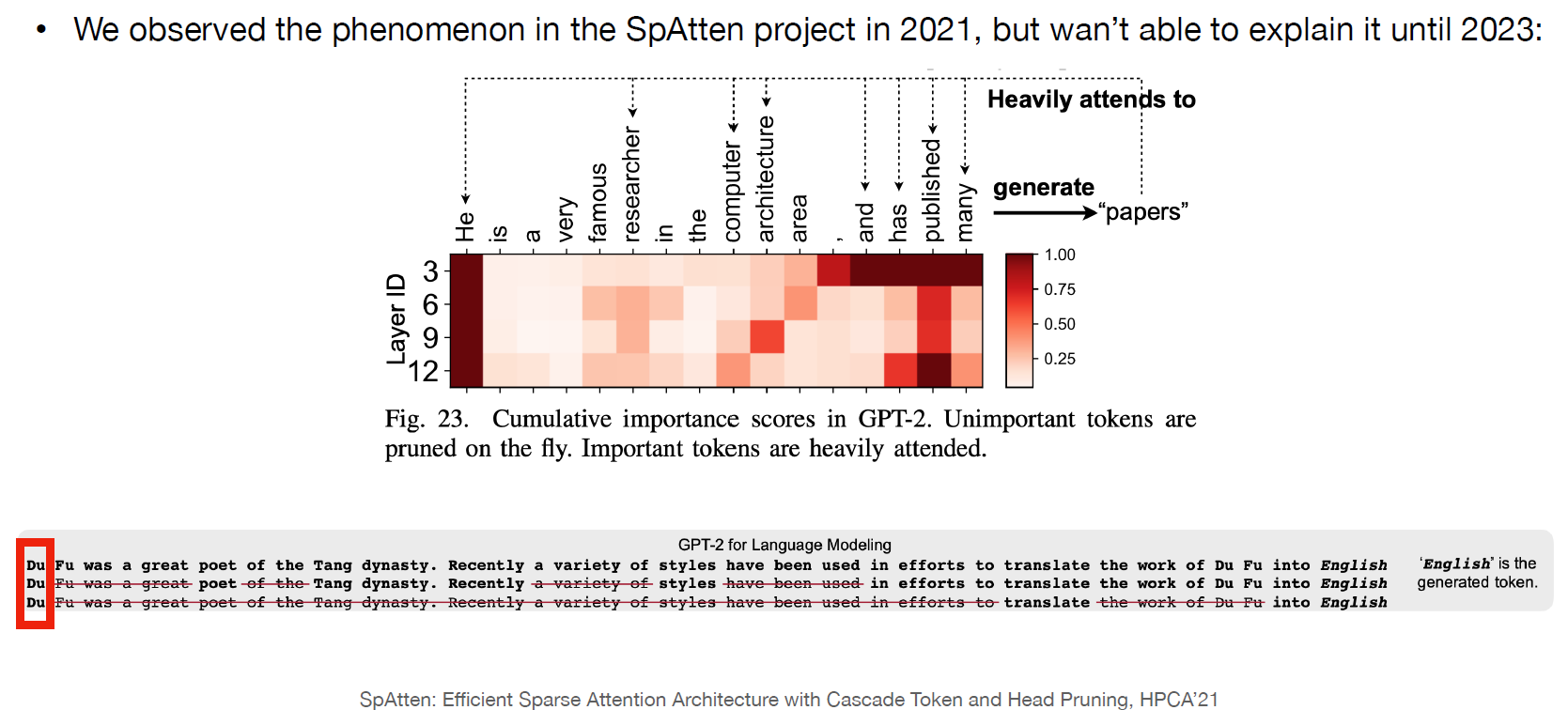上圖是在說明 “papers” 這個 token 的 attention map, 可以觀察到 “papers” 跟開頭第一個 token “He” 有很強的 attention 結果.
這有點怪… 照理說這兩個 tokens 應該沒啥特別關聯阿
再看上圖下面那三句話的例子
可以看到很多 tokens 都可以被 prune 掉而不影響產生最後的 token “English”
但是唯獨不能 prune 掉第一個 token “Du”
“Du Fu” 中文是杜甫, 他是以前唐朝的一位詩人, 他的姓氏 “Du” 跟 “English” 應該沒有關聯才對.
他們做了更多的觀察, 發現這個現象在很多 layers 都如此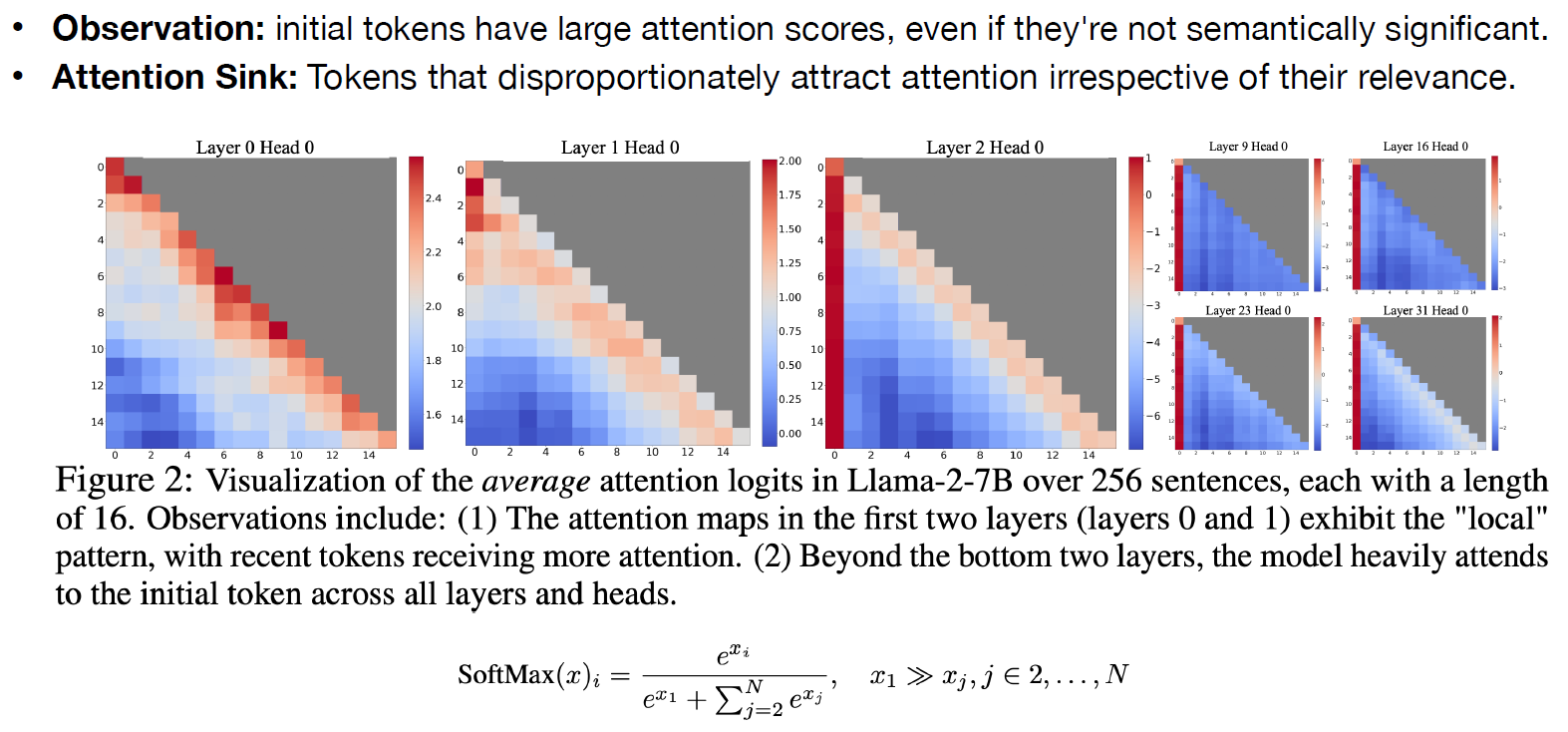
1st token 常常都是大家的關注點, probability 很容易非常高.
但為什麼? 又為何是 1st token 呢?
其實這是因為 auto-regressive 的時候 1st token 永遠會在所有的 attention KV-cache 中, 當沒有任何想要關注的 tokens 的時候, 總是可以把 1st token 當垃圾桶去 attention!
這個現象 Song Han 他們稱為 Attention Sink.
Sink 中文是水槽, 有點像是不知道關注哪裡的時候, 就往那裏跑. 好的命名能讓人一聽就記住.
因此 Song Han 他們就提出 StreamingLLM, 意思就是 window attention 的時候, 永遠會 append 1st token 在 window 的開頭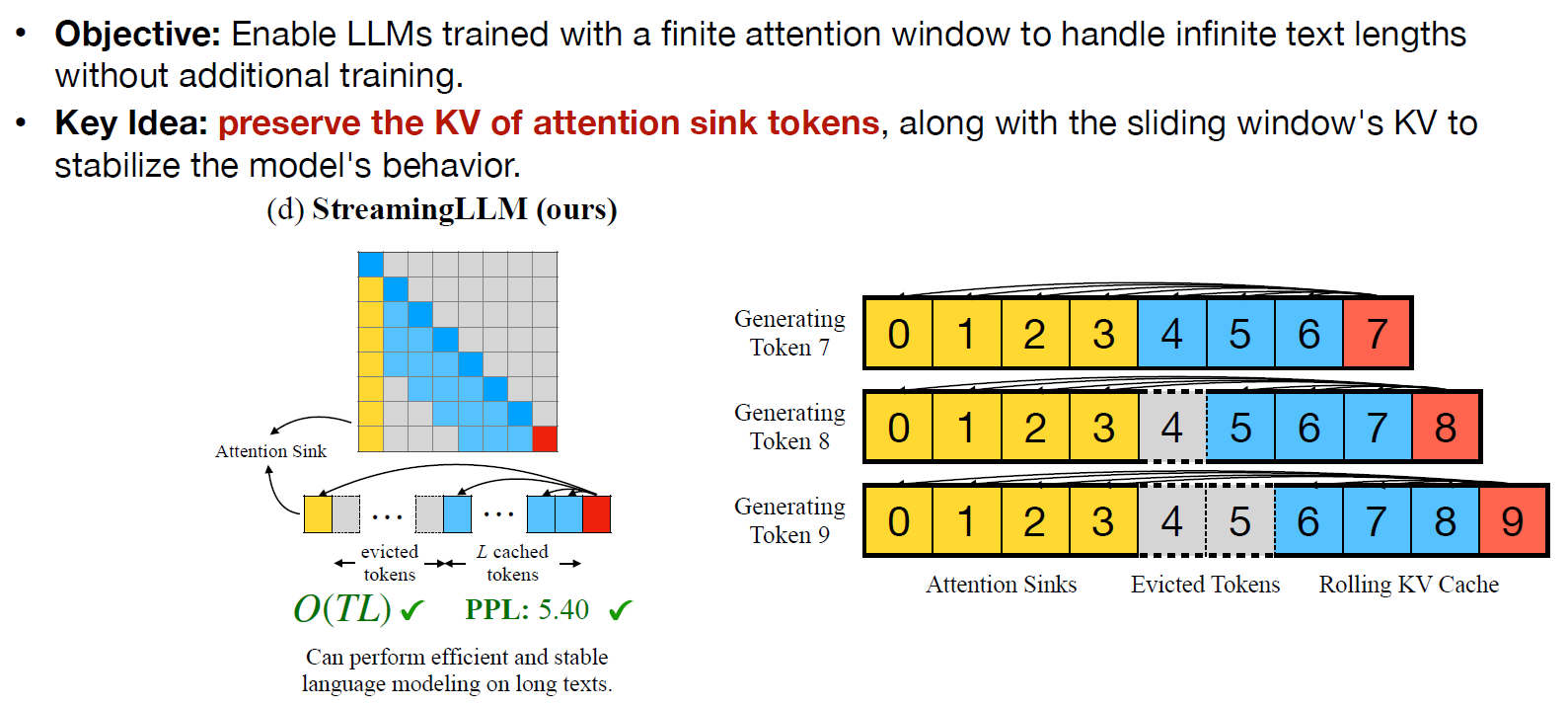
很神奇的是, 一旦這麼做了計算量和 PPL 全部都好了
Song Han 他們也做了一些實驗, 譬如讓 1st token 的 embedding 是可學的, 還有不只加入 1st token, 前幾個 tokens 都可以一起加入等等的實驗, 詳細可參考他們論文
回頭看 K, V Padding Zero Vector
到這可能讀者已經猜出來為什麼要 padding zero vector 了
這個 padding 的 zero vector 其作用就相當於 1st token 的功能.
當沒有任何 tokens 想要 attention 的時候, 給 softmax 一個 “出口”
觀察 softmax 公式, 把第一個 token embedding $x_1$ 拉出來並定義其為 zero , $x_1=0$.
$$\begin{align*}
(\text{softmax}(\mathbf{x}))_i=
\frac{e^{x_i}}{e^{\color{orange}{x_1}}+\sum_{j=2}^N e^{x_j}}
=\frac{e^{x_i}}{e^{\color{orange}{0}}+\sum_{j=2}^N e^{x_j}} \\
=\frac{e^{x_i}}{\color{orange}{1}+\sum_{j=2}^N e^{x_j}}=:(\text{softmax}_{\color{orange}{1}}(\mathbf{x}))_i
\end{align*}$$ 我們稱這樣的 $\text{softmax}$ (第一個 token 為 $0$) 為 $\text{softmax}_{\color{orange}{1}}$. [參考自 Attention Is Off By One]
以前當所有 token 都不想關注的時候
就算把他們 query-key 的內積結果都拉到 $-\infty$ 也不會讓它們的 attention map 機率變成 $0$.
$$\begin{align*}
\lim_{x_1\rightarrow-\infty}\cdots\lim_{x_k\rightarrow-\infty}(\text{softmax}(\mathbf{x}))_i=\frac{1}{k}>0
\end{align*}$$ 但如果是 $\text{softmax}_{\color{orange}{1}}$ 的話能真正讓機率變成 $0$.
$$\begin{align*}
\lim_{x_1\rightarrow-\infty}\cdots\lim_{x_k\rightarrow-\infty}(\text{softmax}_{\color{orange}{1}}(\mathbf{x}))_i=0
\end{align*}$$ 讓機率變成 $0$ 也就達到了 “沒有任何想要 attention” 的效果了!
這就是為什麼 Key 要 append zero vector.
注意到 Value 也同樣要 append zero vector.
這是因為當 attention sink 現象發生的時候 (沒有想要 attention 的情況)
Sink token 的機率最高 ($\approx1$), 所以 sink token 的 value 會決定了這次 attention block 的結果 value
為了讓 attention block 失去作用, 所以設定 sink token 的 value 為 zero vector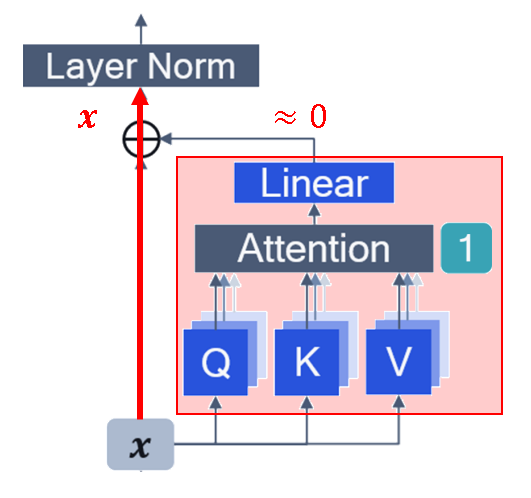
相當於上圖紅色方框的 attention block 什麼都不做, 所以輸出直接等於輸入 $\mathbf{x}$. 這等同於模型在這個 layer 什麼都不做, “do-nothing”.
Conclusions
其實 Qualcomm 的這篇論文 (Quantizable Transformers: Removing Outliers by Helping Attention Heads Do Nothing, arXiv 2023) 也同樣梳理了 attention sink 的現象和其原因
不只發生在 LLM, 在圖像的 ViT 架構也是如此
總歸來說, 我們需要為 softmax 找到一個 “出口”, 當沒有想要 attention 的時候, 有個垃圾桶的 token 去關注.
對於 Key 和 Value 都 append 一個 zero vector 是非常簡單且有用的方法 (見文章開頭的圖)
另外, 這種 softmax 也是造成 Transformer 有很大的 outlier 的原因之一 (詳見剛提到的 Qualcomm 論文) 而這些 outliers 正是 Transformer 難以 PTQ 的主要兇手!
改成用 $\text{softmax}_{\color{orange}{1}}$, 或是 Qualcomm 論文 提的 clipped softmax 和 gating 方法比較能從根源解決這問題. 而 SmoothQuant, AWQ, … 比較像是事後補救
Softmax 硬要選的原罪… 有時候我們反而應該什麼都不做
不強求, 順其自然, 阿咪陀佛… (诶不是, 跑題了)