⚠️ [提醒]: 本篇難度可能偏高, 有些地方不會從頭開始解釋, 畢竟主要給自己筆記的, 請讀者見諒.
筆記動機是由於之前陸陸續續讀過 (連結為之前的筆記們):
- [Score matching]: Langevin dynamics 可以使用 score function ($\nabla\log p_{data}$) 來取 sample, 取出來的 sample 具有 $p_{data}$ 的分佈 (由 Fokker-Planck Equation 的定理可證). 因此我們要做的就是訓練一個 NN $s^\theta(x)\approx \nabla\log p_{data}(x)$, 這樣就能在 Langevin dynamics 中使用 $s^\theta$ 來對 $p_{data}$ 採樣了
- [Denoised diffusion model]: 訓練出能去噪 (denoise) 的 NN model (加高斯噪聲的過程稱 forward process, 去噪稱 backward). 由於無法直接做 MLE (Maximal Likelihood), 因此訓練目標函式改為優化 MLE 的 lower bound, 稱 ELBO (Evidence Lower Bound). 藉由訓練出的 denoised model, 一步一步還原乾淨資料.
- [Flow matching]: 從已知且容易採樣的 $p_{init}$ 採樣出初始 sample $x_0$, 根據學到的 vector field $u_t^\theta$ 來更新 trajectory $\{x_t\}_{0\leq t\leq1}$, 最終達到的 $x_1$ 滿足資料分布 $p_{data}$. 如何設計並訓練這樣的 vector field $u_t^\theta$ 可說是非常精彩, 也會用到物理中的 Continuity Equation (質量守恆).
我心理總認為這些東西應該有非常深刻的關聯 🤔, 但就是缺乏一個統一的框架來把這些觀念融合起來.
直到我看到 MIT 這門課程: Introduction to Flow Matching and Diffusion Models 的一些內容. (👍🏻 大推! 👍🏻)
簡直醍醐灌頂, 因此想筆記下來這個統一的框架. 正文開始
Flow/Score matching or diffusion model 這類的生成式 AI, 本質上在做的事情是從一個已知且容易採樣的 $p_{init}$ 分布出發, 找出一路變化到目標分布 $p_{data}$ 的過程.
中間變化的機率分布 $\{p_t(x)\}_t,0\leq t\leq 1$ 我們稱為 probability path.
因此目標就是設計有效的 probability path 使得滿足頭尾我們要求的 $p_{init}$ 和 $p_{data}$.
Meta 的 [github repo] 這張圖把 flow matching 精隨完全呈現了: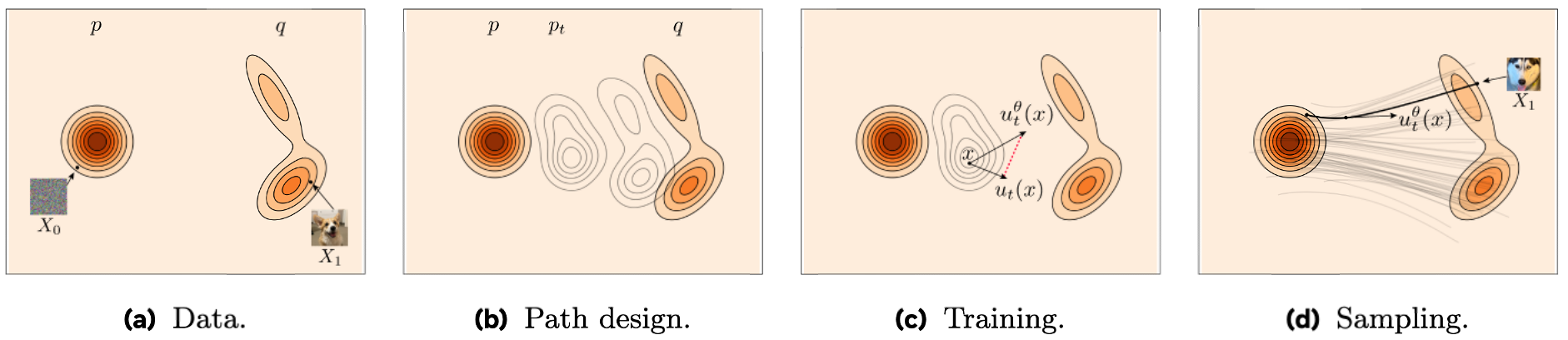
(a) 表明目標的頭尾分佈長相, $p_{init}$ 和 $p_{data}$.
(b) 設計好 vector field $u_t$ 和其對應的中間變化過程的 probability path $\{p_{t}\}_t$.
(c) 訓練 NN $u_t^\theta$ 逼近 vector field $u_t$.
(d) 從採樣的 $x_0\sim p_{init}$ 出發, 套用學到的 $u_t^\theta$ 一路得到 $x_1\sim p_{data}$.
Flow Matching 的 ODE 更新方式和 Vector Field 的設計
總歸來說給定初始位置 $x_0$, 整條 path $\{x_t\}_t,0\leq t\leq 1$ (稱為 flow) 為如下的 ODE (Ordinary Differential Equations) 解:
$$\begin{align}
\boxed{d X_t=u_{t}^\text{flow}(X_t)dt} \\
\text{initial condition}:\quad X_0=x_0
\end{align}$$ 注意到 $X_t$ 是 random variable, $0\leq t\leq 1$.
其中 $u_t^\text{flow}(x)$ 表示位置 $x$ 的 gradient vector. 可理解為順時的位置變化, 即速度.
一般來說我們可以採用例如最簡單的 Euler method 來做數值逼近找出 flow
$$\begin{align}
x_{t+h}=x_t+hu_t^\text{flow}(x_t)
\end{align}$$ 經過聰明的研究人員設計出 $u_t^\text{flow}(x)$ 後, 其所對應的機率分布 $\{p_t(x)\}_t,0\leq t\leq 1$ 能滿足頭尾 $p_{init}$ 和 $p_{data}$ 的要求.
▶️(點擊展開) 如何設計 $u_t^\text{flow}(x)$ 滿足上述的機率分佈呢?
(可跳過, 不影響本篇要講的重點)
設計方法比較精妙, 先定義出 conditional probability path 需滿足 $p_0(\cdot|z)=p_{init}$ 和 $p_1(\cdot|z)=\delta_z$, 其中 $\delta_z$ 為 Dirac delta function, $z\sim p_{data}$.
再設計出能滿足這種 $p_0(\cdot|z), p_1(\cdot|z)$ 的 conditional vector field $u_t^\text{flow}(\cdot|z)$.
(使用 Gaussian probability path $p_t(x|z)=\mathcal{N}(\alpha_tz,\beta_t^2I)$ 的話, 則有唯一 analytical solution 的 $u_t^\text{flow}(\cdot|z)$)
接著定義 $u_t^\text{flow}(x)=\int u_t^\text{flow}(x|z)[p_t(x|z)p_{data}(z)/p_t(x)]dz$, 則此 $u_t^\text{flow}(x)$ 產生的 $p_t(x)$ 就能滿足頭尾 $p_{init}$ 和 $p_{data}$ 的要求.
所以目標就是訓練 NN $u_t^\theta(x)\approx u_t^\text{flow}(x)$ (因為根據上面的定義很難算出來), 因此實際上是透過訓練 $u_t^\theta(x)\approx u_t^\text{flow}(x|z)$ 不僅可行而且等價.
詳細請參考之前筆記.
擴展成 Langevin Dynamics 的 SDE 更新方式, 得到 Score Matching
如果我們將 flow matching 的 ODE 更新方法改成如下的 SDE (Stochastic Differential Equations)
$$\begin{align}
\boxed{ dX_t=u_t^\text{score}(X_t)dt+
{\color{orange}{\sigma_tdW_t}} }
\\
\text{initial condition}:\quad X_0=x_0
\end{align}$$ 其中 $W_t$ 是 Brownian motion, (或稱 Wiener process). $\sigma_t\geq0$ 且連續稱 diffusion coefficient (是事先定義好的).
寫成離散的更新步驟比較好理解:
$$\begin{align}
X_{t+h}=X_t+hu_t^\text{score}(X_t)+\sigma_t(W_{t+h}-W_t) \\
\Longrightarrow X_{t+h}=X_t+hu_t^\text{score}(X_t)+\sigma_t\sqrt{h}\epsilon,\quad \epsilon\sim\mathcal{N}(0,I)
\end{align}$$ 如果 $u_t^\text{score}$ 定義如下:
$$\begin{align}
\boxed{ u_t^\text{score}(X_t):=u_t^\text{flow}(X_t)+
{\color{orange}{\frac{\sigma_t^2}{2}\nabla\log p_t(X_t)}} }
\end{align}$$ 其中 $\nabla\log p_t(x)$ 稱為 score function. 這裡的 gradient 寫清楚一點是 $\nabla_x$, 但以下都簡寫為 $\nabla$.
式 (8) 所定義的 vector field $u_t^\text{score}$ 已經不是 deterministic 了, 因為 $X_t$ 是 random variable. 所以看成是 “stochastic” vector field 也滿合理的.
💡 則使用 $u_t^\text{score}$ (8) 去做 SDE (4) 更新步驟, 其所產生的 probability path $\{p_t(x)\}_t,0\leq t\leq 1$ 會跟用 $u_t^\text{flow}(x)$ 的 ODE (1) 產生的 probability path 一樣!!
這個結論相當重要, 讓我們有機會把 flow matching 和 score matching 從本質上關聯起來.
(參考 arxiv Theorem 13 (SDE extension trick))
直覺解釋為因為加入了 SDE 的 Brownian motion 的隨機項, 則 SDE 多出來的橘色 term 有點像是扮演抵銷的角色.
這個結論的證明需要使用 Fokker-Planck Equation, 即需證明 SDE (4) 和 (8) 滿足 F-P equation. (參考 arxiv Proof of Theorem 13. @p20)
由於之前 flow matching 已經訓練出 NN ${\color{red}{u_t^\theta}}(x)\approx u_t^\text{flow}(x)$ 了, 所以現在我們只要訓練另一個 NN ${\color{orange}{s_t^{\theta}}}(x)\approx \nabla\log p_t(x)$, 我們就能用下面的 SDE 方式更新了:
$$\begin{align}
\boxed{dX_t=\left[{\color{red}{u_t^\theta}}(X_t)+\frac{\sigma_t^2}{2}{\color{orange}{s_t^\theta}}(X_t)\right]dt
+
\sigma_tdW_t }
\\
\text{initial condition}:\quad X_0=x_0
\end{align}$$ 注意到 ${\color{red}{u_t^\theta}}$ 和 ${\color{orange}{s_t^\theta}}$ 共享參數 $\theta$, 意思是同一個 NN predicts 兩個數值.
以上正是 vallina 的 score matching 作法.
當然還有一些重要細節, 例如 ${\color{orange}{s_t^{\theta}}}(x)$ 不是去逼近 $\nabla\log p_t(x)$ (因為實務上辦不到), 而是如同 flow matching 的訓練改為逼近 $\nabla\log p_t(x|z)$. 然後這樣做是等價的.
(參考 arxiv Proof of Theorem 20. @p28)
另外值得一提的是, 當訓練好 score function 的 NN ${\color{orange}{s_t^\theta}}$ 之後, diffusion coefficient $\sigma_t$ 可以自由設定, 只要 $\geq0$ 且連續即可.
所以可以看到當 $\sigma_t=0$ 的話, score matching reduce 成 flow matching 了.
Gaussian Probability Path 的 Score Matching 訓練
我們知道若為 Gaussian probability path $p_t(x|z)=\mathcal{N}(\alpha_tz,\beta_t^2I)$ 的情形, 其 conditional vector field $u_t^{flow}(x|z)$ 為 (推導參考之前筆記): $$\begin{align}
u_t^{flow}(x|z)=\left(\dot{\alpha}_t-\frac{\dot{\beta}_t}{\beta_t}\alpha_t\right)z+\frac{\dot{\beta}_t}{\beta_t}x
\end{align}$$ 繼續做一些推導:
$$\begin{align*}
=\left(\beta_t^2\frac{\dot\alpha_t}{\alpha_t}-\dot\beta_t\beta_t\right)
\left(\frac{\alpha_tz-x}{\beta_t^2}\right)+\frac{\dot\alpha_t}{\alpha_t}x \\
=\left(\beta_t^2\frac{\dot\alpha_t}{\alpha_t}-\dot\beta_t\beta_t\right)\nabla\log p_t(x|z) + \frac{\dot\alpha_t}{\alpha_t}x
\end{align*}$$ 推導用到了 $\nabla\log p_t(x|z)=(\alpha_tz-x)/\beta_t^2$ (由高斯分布定義得知). 因此我們得到 $u_t^{flow}(x|z)$ 和 $\nabla\log p_t(x|z)$ 的關聯.
同樣的也有 $u_t^{flow}(x)$ 和 $\nabla\log p_t(x)$ 的關聯. 統一整理如下:
$$\begin{align}
u_t^{flow}(x|z)=\left(\beta_t^2\frac{\dot\alpha_t}{\alpha_t}-\dot\beta_t\beta_t\right)\nabla\log p_t(x|z) + \frac{\dot\alpha_t}{\alpha_t}x \\
u_t^{flow}(x)=\left(\beta_t^2\frac{\dot\alpha_t}{\alpha_t}-\dot\beta_t\beta_t\right)\nabla\log p_t(x) + \frac{\dot\alpha_t}{\alpha_t}x
\end{align}$$ 上面的結果表明只要得到 $\nabla\log p_t$, 則 $u_t^{flow}$ 可透過上式也得到. 即 vector field 和 score function 在 Gaussian probability path 假設下等價!
所以 vallina 的 score matching 作法 (9), (10) 可改寫成:
$$\begin{align}
\boxed{ dX_t=\left[
\left(\beta_t^2\frac{\dot\alpha_t}{\alpha_t}-\dot\beta_t\beta_t+\frac{\sigma_t^2}{2}\right){\color{orange}{s_t^\theta}}(X_t) + \frac{\dot\alpha_t}{\alpha_t}X_t
\right]dt
+
\sigma_tdW_t }
\\
\text{initial condition}:\quad X_0=x_0
\end{align}$$ (14) 是因為我們將 vector field 用 score function 替代:
$$\begin{align*}
\boxed{ {\color{red}{u_t^\theta}}(X_t)=
\left(\beta_t^2\frac{\dot\alpha_t}{\alpha_t}-\dot\beta_t\beta_t\right)
{\color{orange}{s_t^\theta}}(X_t) + \frac{\dot\alpha_t}{\alpha_t}x }
\end{align*}$$ 上面的 SDE (14) 就是 score matching 的更新方式, 也是一般指的 denoised diffusion model.
Flow Matching Model with Guided Conditions
給定 guided conditions $y$, 可以是 prompt, class index, images, audio 等等, 希望能產生對應的 $x$.
式 (13) 可以看成 $u_t^\text{flow}$ 為 $x$ 和 $\nabla\log p_t$ 的線性組合
$$\begin{align}
u_t^\text{flow}(x|y)=a_tx+b_t\nabla\log p_t(x|y) \\
,\text{where} (a_t,b_t)=\left(\frac{\dot\alpha_t}{\alpha_t},\frac{\dot\alpha_t\beta_t^2-\dot\beta_t\beta_t\alpha_t}{\alpha_t}\right)
\end{align}$$ 根據 Bayes rule 繼續推導
$$\begin{align*}
u_t^\text{flow}(x|y)=a_tx+b_t\nabla(\log p_t(y|x)+\log p_t(x) - \log p_t(y)) \\
=(a_tx + b_t\nabla\log p_t(x)) + b_t\nabla\log p_t(y|x) \\
=u_t^\text{flow}(x) + b_t\nabla\log p_t(y|x)
\end{align*}$$ $p_t(y|x)$ 通常表示 posterior probability, 用 MNIST 0~9 數字 images 來舉例, $y$ 就是 class index 0~9. 所以 $p_t(y|x)$ 就表示給定 image $x$ 屬於 class $y$ 的機率.
因此 guided vector field $u_t^\text{flow}(x|y)$ 就是 unguided vector field $u_t^\text{flow}(x)$ 加上一個 guided score $\nabla\log p_t(y|x)$.
通常人們為了加強 guided 效果, 會把 guided score 乘上一個更大的權重 $w>1$ (稱 guided scale), 因此實際上在用的 guided vector field $\tilde{u}_t^{flow}$ 為:
$$\begin{align}
\tilde{u}_t^{flow}(x|y)=u_t^\text{flow}(x) + wb_t\nabla\log p_t(y|x)
\end{align}$$ 注意到當 $w\neq 1$ 時, $\tilde{u}_t^\text{flow}(x|y)\neq u_t^\text{flow}(x|y)$, 已經不是正確數學上的 guided vector field 了. 縱使如此, 實務上使用 $\tilde{u}_t^\text{flow}(x|y)$ 仍然表現很好.
使用 (18) 的一個缺點是必須要額外訓練一個 NN 計算 posterior probability. 如果 $y$ 是簡單的 class index 那還好, 但對於常見的如 text prompt 就做不太到了.
因此會演變為以下介紹的 Classifier-Free Guidance (CFG) 的 flow matching
繼續使用 Bayes rule 推導 (18)
$$\begin{align*}
= u_t^\text{flow}(x) + wb_t(\nabla\log p_t(x|y)-\nabla\log p_t(x)) \\
= u_t^\text{flow}(x) - (wa_tx+wb_t\nabla\log p_t(x)) + (wa_tx+wb_t\nabla\log p_t(x|y)) \\
=(1-w)u_t^\text{flow}(x) + wu_t^\text{flow}(x|y)
\end{align*}$$ 重寫一下我們得到
$$\begin{align}
\tilde{u}_t^{flow}(x|y) = (1-w)u_t^\text{flow}(x) + wu_t^\text{flow}(x|y)
\end{align}$$ 實際上訓練 NN 時, unguilded vector field $u_t^\text{flow}(x)$ 視為某種情況的 guided vector field $u_t^\text{flow}(x|\phi)$, 即 $y=\phi$ 條件下的 guided condition.
所以 $u_t^\text{flow}(x|\phi)$ 與 $u_t^\text{flow}(x|y)$ 就可以一起訓練. 只要取 $(x,y)\sim p_{data}(X,Y)$ 時, 有某個機率設定 $y=\phi$ 即可.
演算法流程如下:

最後也可以把 guided condition 拓展到 score matching, 非常類似, 這裡就省略紀錄 (參考 arxiv 5.1.2 Guidance for Diffusion Models @p41).
最後也非常推薦課程的 Colab juypter notebook, 真的下次時做會更有幫助.