RL的數學原理: 趙世鈺課程濃縮筆記

發表於 | 分類於 | [object Object]

📔 筆記內容: 赵世钰老師 “强化学习的数学原理” 課程 (也推薦用 Notion版本 來閱讀)
很高興我初次學習 RL 就是透過這門課, 讓我扎實理解其背後的數學和邏輯
老實說 RL 方法很多很雜, 套句趙老師的話, RL 數學很深, 結構性又很強, 一環扣一環
如果沒有這堂課這樣循序剖析和從數學出發解釋的話, 我自己應該很難入門, 謝謝這門課的赵世钰老師! 🙏🏻

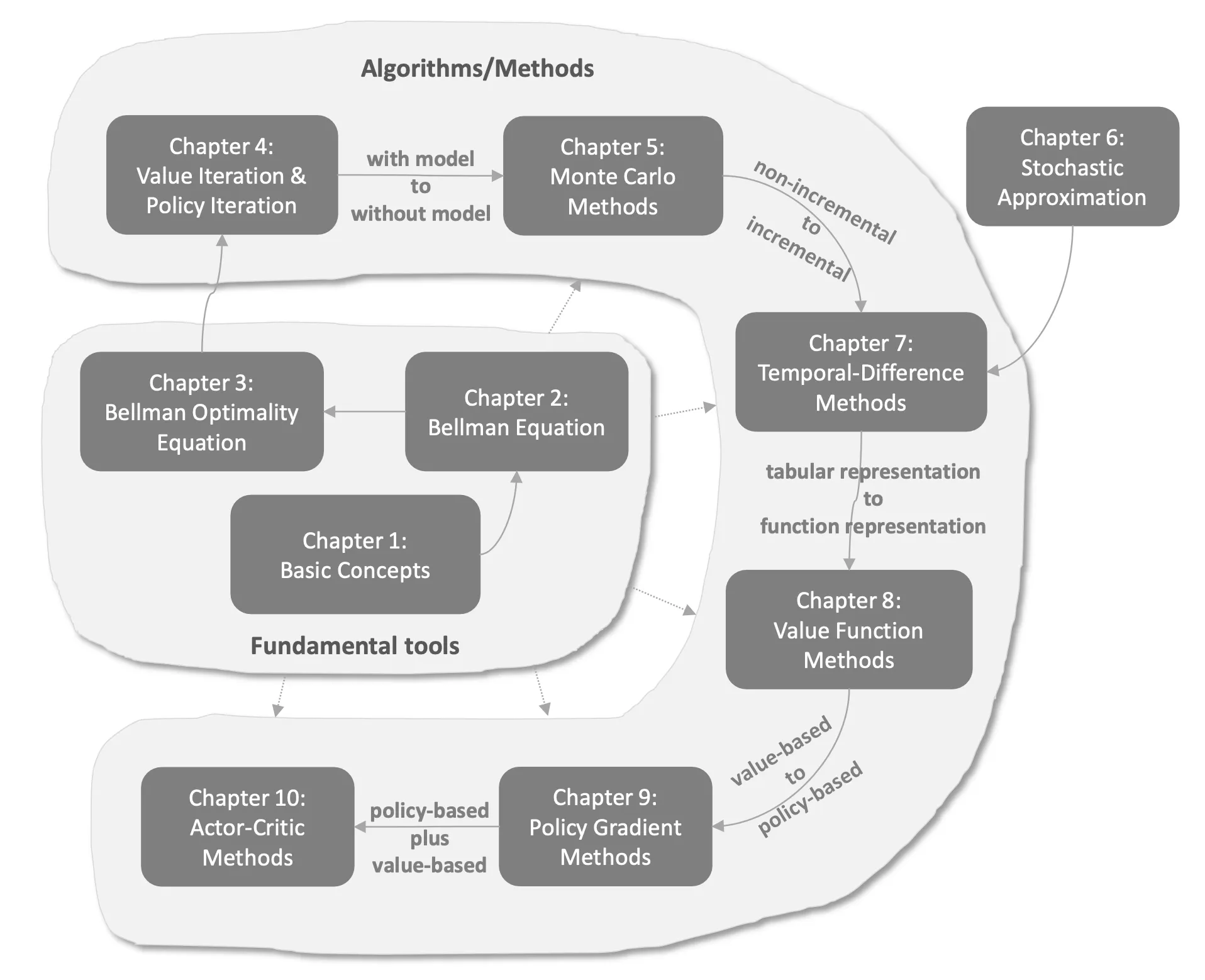
本篇筆記方式盡量濃縮, 而每個章節更詳細的筆記參考:
 $\circ$ RL(1): Fundamentals of Reinforcement Learning
 $\circ$ RL(2): Sample-based Learning Methods
 $\circ$ RL(3): Prediction and Control with Function Approximation

挖坑給自己: 下一次讀 Kevin Murphy 的 reinforcement learning [arxiv]

[Ch1]: Basic Concepts

RL 的環境設定 reward $r$, action $a$, state $s$, policy $\pi(a|s)$ 等的初步介紹自行查資料即可
重點是套用 Markov Decision Process (MDP) 的框架.
Markov Decision Process (MDP) 給定前一次 state $s$ 和前一次 action $a$, 我們可以定義 state 和 reward 的 distribution:
$p(s',r|s,a)\triangleq Pr\{S_t=s',R_t=r|S_{t-1}=s,A_{t-1}=a\}$ For all $s',s\in\mathcal{S}$, $r\in\mathcal{R}$ , and $a\in\mathcal{A}(s)$. Action space 是從 state 定義出來的.
所以 $p:\mathcal{S}\times\mathcal{R}\times\mathcal{S}\times\mathcal{A}\rightarrow[0,1]$. ($p$ 稱 dynamics function of MDP)

知道這個四元 $p(s',r|s,a)$ 的機率就稱 with model 的 RL 方法, 反之就是 without model 的方法

Return $G_t$ 定義為 (有些人稱 total rewards)
$$\begin{align*} G_t\triangleq R_{t+1}+\gamma R_{t+2}+\gamma^2R_{t+3}+\cdots \\ =\sum_{k=0}^\infty\gamma^kR_{t+k+1}=R_{t+1}+\gamma G_{t+1} \end{align*}$$ Return 取期望值的話 (expected return) 就稱 Value (價值) ← RL 目標就是找到能最大化 value 的 policy $\pi(a|s)$.

[Ch2]: Bellman Equation

State value and action value 不同形式的 Bellman equations 推導來源:

  • State Value $v_\pi(s)$ Elementwised form [ref]
  • State Value $v_\pi(s)$ Expectation form [ref]
  • State Value $v_\pi(s)$ Matrix Vector form [ref]
  • Action Value $q_\pi(s,a)$ Elementwised form [ref]
  • Action Value $q_\pi(s,a)$ Expectation form [ref]

Bellman equation 就是在做 PE (Policy Evaluation), 即給定一個 policy $\pi$ 評估每個 state $s$ 的 expected return (value)
可以用 iterative 方法求解: $v_{k+1}=r_\pi+\gamma P_\pi v_k,\quad k=0,1,2,...$ [ref]

[Ch3]: Bellman Optimality Equation

原先的 Bellman equation 都是給定一個 policy $\pi$ 情況下求解的 state value or action value. 但 RL 目的是要找出什麼樣的 policy 能得到最大的 value (optimal policy), 光評估給定的一個 policy 的 value 是不夠的.
BOE 現在將 $\pi$ 也當成要求解的參數, 直接對 Bellman equation 做最佳化 (多了 $\max_\pi$), 因此 BOE:
$$\begin{align*} {\color{orange}{v(s)}}={\color{red}{\max_{\pi}}}\left[\sum_a {\color{orange}{\pi(a|s)}}\left(\sum_{r}p(r|s,a)r + \gamma\sum_{s'}p(s'|s,a){\color{orange}{v(s')}}\right)\right],\quad\forall s\in\mathcal{S} \\ =\max_{\pi} \sum_a\pi(a|s)q_\pi(s,a) ,\quad\forall s\in\mathcal{S}\\ \text{Matrix Vector form}\quad\Longrightarrow v=f(v)\triangleq \max_\pi(r_\pi+\gamma P_\pi v) \end{align*}$$ 要求解的 variables 為 ${\color{orange}{v(s)}}$ 和 ${\color{orange}{\pi(a|s)}}$.
可以證明 $f$ 是 contraction mapping, 則 $\exists!$ fixed point $v_\ast$: $v_\ast=f(v_\ast)=\max_\pi(r_\pi+\gamma P_\pi v_\ast)$ 因此 $v_\ast$ 可透過 contraction mapping theorem 的疊代方法找到: $v_{k+1}=f(v_k)=\max_\pi(r_\pi+\gamma P_\pi v_k),\quad k=0,1,2,...$ (其中 initial 可以是任意)
找到 $v_\ast$ 後, 令 $\pi_\ast\triangleq\arg\max_\pi(r_\pi+\gamma P_\pi v_\ast)$ 即為 optimal policy 了
在疊代過程中求解這個 $\max_\pi(r_\pi+\gamma P_\pi v_k)$ 的最佳的 $\pi_{k+1}$ 使用 Greedy Optimal Policy:
$$\pi_{k+1}(a|s)=\left\{ \begin{array}{cl} 1, &a=a_k^\ast(s) \\ 0, &a\neq a_k^\ast(s) \end{array} \right. \\ ,\text{where }a_k^\ast(s)=\arg\max_a q_k(s,a)$$ $\pi_{k+1}$ 是 deterministic 的 (one-hot vector distribution)
注意到 BOE 是 Bellman equation 的其中一種情況而已, 滿足 BOE 的 policy 為 optimal policy
如果看 action value 的話, 其 **BOE 為:
$$\begin{align*} {\color{orange}{q(s,a)=\mathbb{E}\left[\left. R_{t+1}+\gamma\max_{a'}q(S_{t+1},a')\right|S_t=s,A_t=a \right]}} \end{align*}$$


▶️(點擊展開) Action Value BOE 推導 [ref]
$$\begin{align*} q(s,a)=\mathbb{E}\left[\left. R_{t+1}+\gamma\max_{a'}q(S_{t+1},a')\right|S_t=s,A_t=a \right] \\ =\sum_r p(r|s,a)r + \gamma\sum_{s'}p(s'|s,a)\max_{a'\in\mathcal{A}(s')}q(s',a') \\ \end{align*}$$ 對兩邊對 action $a$ 取 $\max$ 變成
$$\begin{align*} \max_{a\in\mathcal{A}(s)}q(s,a) = \max_{a\in\mathcal{A}(s)}\left[ \sum_r p(r|s,a)r + \gamma\sum_{s'}p(s'|s,a)\max_{a'\in\mathcal{A}(s')}q(s',a') \right] \end{align*}$$ 定義 $v(s)\doteq\max_{a\in\mathcal{A}(s)}q(s,a)$, 改寫上式
$$\begin{align*} v(s)=\max_{a\in\mathcal{A}(s)}\left[ \sum_r p(r|s,a)r + \gamma\sum_{s'}p(s'|s,a)v(s') \right] \\ =\max_\pi\sum_{a\in\mathcal{A}(s)}\pi(a|s)\left[ \sum_r p(r|s,a)r + \gamma\sum_{s'}p(s'|s,a)v(s') \right] \end{align*}$$ 這正好就是 State Value 的 BOE

[Ch4]: Value Iteration & Policy Iteration

求解 BOE 可以直接幫我們找出 optimal state value 是多少, 以及對應的 optimal policy 是什麼
根據 contraction mapping theorem 可以從任意的 initial value $v_0$ 出發, 只要一直疊代: $v_{k+1}=f(v_k)=\max_\pi(r_\pi+\gamma P_\pi v_k) ,$ $k=0,1,2,...$, 就能解
因此有了 Value Iteration 算法, 其中 policy update 用 Greedy Optimal Policy.
順序反過來的話, Policy iteration 先從一個任意的 policy $\pi_0$ 出發, 利用上面 Ch2 的 PE (Policy Evaluation) 我們可以評估在該 policy 下的 state value $v_{\pi_0}$.
(注意到這是合法的 state value, 跟 value iteration 的 $v_0$ 不一樣)
有了對應的 state value $v_{\pi_0}$ 一樣利用 Greedy Optimal Policy 更新 policy, 即 policy improvement (PI) 找到更優的 policy. 重複 iteration 就是策略迭代算法.
下圖左和右分別是 Value & Policy iteration 算法
Policy iteration 的收斂性證明需要用到 Value iteration 收斂的性質. 其他證明如能確保找到的 policy or value 是 optimal 的請參考 Week4 筆記.
最後它們都是 truncated policy iteration 的特例
注意到, Policy iteration 的 PE 理論上要收斂到無窮多步才能求出正確的 value 值 $v_{\pi_k}$, 但如果只做一步 update 其實就是 value iteration 的做法, 更多請參考 Week4 筆記.
在做 policy or value iteration 的時候, 都會對所有 state 做 for loop
事實上可以很彈性, 可以 random 對 state 做, 也可以馬上 inplace 更新 state value, 也可以每次變動 truncated $j$ 步. 這樣做的好處是當 states 數量很多的時候 (甚至連掃過一次所有 states 都很難) 還是能做 RL.
這種更 general 的方法 Sutton and Barto 課本稱 Generalized Policy Iteration (GPI).

[Ch5]: Monte Carlo Methods for Prediction & Control

在 Policy iteration 算法中的 PI step 觀察其 Elementwised form 發現就是根據現在估計的 action value $q_k(s,a)$ 來找最佳的policy
那麼這個 action value $q_k(s,a)$ 在沒有模型 (dynamic function) 的情況下就無法用 Bellman equation 來計算
因此改採最原始的定義, 那就可以透過採樣來估計: $q_{\pi_k}(s,a)=\mathbb{E}\left[G_t|S_t=s,A_t=a\right]\approx\frac{1}{N}\sum_{i=1}^Ng^{(i)}(s,a)$.
簡單講, 對每一個 $s\in S,a\in A$ 來說要找出 $N$ 條從 $(s,a)$ 出發的 trajectory (episode), 每一條都算出 return, 然後平均 return 後就當作是期望值.
但這樣對每一個 episode 的數據沒有很好利用, 很沒效率.
例如對某一個 state-action pair $(s_i,a_i)$ 開始的長度 $T$ 的 episode 只拿來估計 $q_{\pi_k}(s_i,a_i)$.
因此有一些很明顯的改進方法, first visit, every visit, 倒過來算 return, 在 PI 階段改成用 $\varepsilon$-greedy 方法解除 exploring starts 限制等等, 詳細看 Week 5 筆記.
反正一樣是 PE & PI 兩階段 (跟 Policy Iteration 算法一樣), 只是 PE 採用有效率的 MC 方法估計

[Ch6]: Robbins-Monro Algorithm 和 Dvoretzky’s Convergence Theorem 筆記

直接參考 blog

[Ch7]: Temporal Difference Learning Methods for Prediction/Control

[State Value 的 TD algorithm 一句話]: Model-free 的 incremental Policy Evaluation
這句話長一點是這樣: 在沒有 dynamic (model) function 情況下給定一個 policy $\pi$ 用 incremental 的方式 (不用等到 episode 結束) 求 state value (解 Bellman equation).

所以還是在做 policy evaluation (如何 incremental 估計 state/action value), 可以想成 Policy iteration 算法的 PE 階段換成 TD method.


▶️(點擊展開) D 算法邏輯推導解釋 (RM 解 root, 該 root 為 Bellman equation 解)
回顧 Bellman Expectation equation: $v_\pi(s)=\mathbb{E}[R_{t+1}+\gamma v_\pi(S_{t+1})|S_t=s],\quad s\in\mathcal{S}$ 對某個特定的 state $s$, 令我們要求解的 $v_\pi(s)$ 為變數 $w$, 我們定義 function $$\begin{align*} g({\color{orange}{w}})\doteq {\color{orange}{w}} - \mathbb{E}[R_{t+1}+\gamma v_{\color{red}{\pi}}(S_{t+1})|S_t=s] \end{align*}$$ 則對 $g$ 求解 root 等價於解出 Bellman Expectation equation.
套用 RM 算法 (參考 Robbins-Monro algorithm), 定義觀測函數 $\tilde{g}$ 為一次的觀測 sample: $\tilde{g}(w,\eta_t)\doteq w-\left[r+\gamma v_\pi(s')\right]$ 其中 $R_{t+1}=r$ 和 $S_{t+1}=s'$. 這是因為在 model-free 的設定下, 我們可以很容易拿到 $(S_t,R_{t+1},S_{t+1})$ 的很多觀測值 $\{(s,r,s')\}$, 這叫 experience sample.
則 RM 算法為: $$\begin{align*} w_{k+1}=w_{k}-a_k\tilde{g}(w_{k},\eta_k),\quad k=1,2,3,... \\ \Longrightarrow w_{k+1}=w_{k}-a_k\left(w_{k}-\left[r+\gamma v_{\color{red}{\pi}}(s')\right]\right),\quad k=1,2,3,... \end{align*}$$ 滿足 RM 算法的收斂條件下, 最後 $w_\infty$ 為 root, 即 $g(w_\infty)=0$: $w_\infty=\mathbb{E}[R_{t+1}+\gamma v_{\color{red}{\pi}}(S_{t+1})|S_t=s]$. 這樣就把 Bellman equation 解出來了.
注意到上述的解 $w_\infty$ 的過程需要用到 ground truth state value $v_{\color{red}{\pi}}$, 實務上使用目前正在估計的 $w_k$ 替代, 因此收斂過程還需嚴格證明, 這裡略過

因此 TD 算法:
$$\begin{align*} {\color{orange}{ \underbrace{v_{t+1}(s)}_{\text{new est.}} = \underbrace{v_{t}(s)}_{\text{current est.}} -\alpha_t(s) [ \overbrace{ v_t(s)-( \underbrace{r+\gamma v_t(s')}_{\text{TD target }\bar{v}_t}) }^{\text{TD error }\delta_t} ] }} ,\\ v_{t+1}(s)=v_t(s),\quad\forall s\neq s_t, \end{align*}$$ 兩個重要的 terms, TD target $\bar{v}_t$ 和 TD error $\delta_t$ 需要記住.
每次 iteration 都會縮短與 TD target $\bar{v}_t$ 的距離, 而 TD error 反應了目前 state value 的估計 $v_t$ 與真實 state value $v_\pi$ 的 ”期望” 差異. 更多參閱它們的特性.
如果 TD 方法改為估計 action value, 一個經典的方法稱為 Sarsa
給定 experience samples $\{(s_t,a_t,r_{t+1},s_{t+1},a_{t+1})\}_t$ (所以 s a r s a 名字就這麼來)
則 Sarsa algorithm 為 :
$$\begin{align*} {\color{orange}{q_{t+1}(s_t,a_t)=q_t(s_t,a_t)-\alpha_t(s_t,a_t)\left[q_t(s_t,a_t)-(r_{t+1}+\gamma q_t(s_{t+1},a_{t+1}))\right]}}, \\ q_{t+1}(s,a) =q_t(s,a),\quad \forall (s,a)\neq(s_t,a_t) \end{align*}$$ 可以看到跟 state value 的 TD algorithm 幾乎一樣, 把 $(s,a)$ 當成是新的 state 這樣看就一樣了, 所以收斂性質一樣.
還有 expected Sarsa, n-step Sarsa 的變形. 也一樣參考 Week 7 的筆記.

最後一個鼎鼎大名的方法, Q-learning
[Q-learning 一句話]: Model-free 的 incremental 解 BOE (Bellman Optimality Equation) 方法
先直接給出 Q-learning 算法
$$\begin{align*} q_{t+1}(s_t,a_t)=q_t(s_t,a_t)-\alpha_t(s_t,a_t)\left[q_t(s_t,a_t)-\left[ {\color{orange}{r_{t+1}+\gamma \max_{a\in\mathcal{A}}{q_t(s_{t+1},a)} }} \right]\right], \\ q_{t+1}(s,a) =q_t(s,a),\quad \forall (s,a)\neq(s_t,a_t) \end{align*}$$ 可以發現同樣只有 TD target 不同, 所以等同於在解決如下的數學問題 (這剛好是 action value 的 BOE):
$$\begin{align*} {\color{orange}{q(s,a)=\mathbb{E}\left[\left. R_{t+1}+\gamma\max_{a'}q(S_{t+1},a')\right|S_t=s,A_t=a \right]}} \end{align*}$$

使用 RM 算法去解 root 就得到上述的 Q-learning 演算法

最後有個統一的視角
算法角度上, 只是 TD target 的不同
因此數學上對應求解的目標函式也就跟著不同

[Ch8]: Value Function with Function Approximation Methods

之前的方法只能處理 state/action value 和 policy 都是 tabular 的形式 (只能是 finite discrete function)

  • Ch8 將 state/action value 推廣成 continuous 形式
  • Ch9 將 policy 推廣成 continuous 形式
  • Ch10 結合 Ch8&9 總結出 Actor-Critic 算法
    本章節介紹的方法都是在做 PE (Policy Evaluation), 也就是還要結合 Policy Improvement (除了 Q-learning&DQN) 才是完整的 policy iteration 算法 (PE+PI).

State value with function approximation

先推廣看看 state value, 我們用 continuous function 來代表, $\hat{v}(s,w)$, 其中 $w$ 表示該 function 的參數
一般來說我們會有這樣的(優化)目標函數, 希望的估計 function $\hat{v}$ 跟目標 $v_\pi$ 在 MSE 視角下 “期望值” 愈小愈好
$$\begin{align*} J(w)=\frac{1}{2}\mathbb{E}_{s\sim {\color{orange}{d_\pi}}}[(v_\pi(S)-\hat{v}(S,w))^2] \end{align*}$$ 期望值的計算採用 steady state $d_\pi$ 的分布, 這是因為 MDP 給定 policy $\pi$ 的情況下會 reduce 成 MC (Markov Process)
MC 在滿足一些條件下會存在 steady state 分布, $d_\pi$, [Ergodic Theorem]

我們說 $J(w)$ 這個目標函式, 其實等價於在解 state value 的 Bellman equation 的 expectation form. 因為 $=0$ 的情況就是滿足平方向裡面為 $0$.

而用 policy $\pi$ 直接採樣 trajectories 後, 搜集到的 $\{s_t\}_t$ 服從 $d_\pi$ 的分佈, 因此套 SGD 就很容易了

$$\begin{align*} w_{t+1}=w_t+\alpha_t( {\color{red}{v_\pi(s_t)}} -\hat{v}(s_t,w_t))\nabla_{w}\hat{v}(s_t,w_t) \end{align*}$$

ground truth 的 $v_\pi$ 我們不知道, 因此有兩種替代方式:

  1. Monte Carlo learning with function approximation
    設定 $v_\pi(s_t)$ 為 $g_t$, 其中 $g_t$ 是從 $s_t$ 出發 (採樣) 直到完成一個 episode 的 return. 則變成 $$\begin{align*} w_{t+1}=w_t+\alpha_t( {\color{red}{g_t}} -\hat{v}(s_t,w_t))\nabla_{w}\hat{v}(s_t,w_t) \end{align*}$$
  2. TD learning with function approximation
    設定 $v_\pi(s_t)$ 為 TD target $r_{t+1}+\gamma\hat{v}(s_{t+1},w_t)$. 則變成 $$\begin{align*} w_{t+1}=w_t+\alpha_t( {\color{red}{r_{t+1}+\gamma\hat{v}(s_{t+1},w_t)}} -\hat{v}(s_t,w_t))\nabla_{w}\hat{v}(s_t,w_t) \end{align*}$$ 其實就變成中間是 TD-error 了 (參考 TD-learning 的公式 (7))
    進一步的如果使用 linear function $\hat{v}(s,w)=\phi(s)^Tw$ 來近似, 其中 gradient 為 $\nabla_w\hat{v}(s,w)=\phi(s)$, 則變成
    $$\begin{align*} w_{t+1}=w_t+\alpha_t({\color{red}{r_{t+1}+\gamma\phi^T(s_{t+1})w_t}}-\phi^T(s_t)w_t)\phi(s_t) \end{align*}$$ 稱為 TD-linear 算法, 我們可以證明 Ch7 學的 tabular TD 算法是這個 TD-linear 的一個特例 [ref]

TD learning with function approximation 的算法更新究竟在優化什麼目標函式, 粗暴點理解是一樣在解 Bellman equation, 詳細見筆記這部分.

Action value with function approximation

再來如果是 action value 做 continuous 推廣的話, 其實方法一樣
Sarsa 的 action value with function approximation 的算法公式:
$$\begin{align*} w_{t+1}=w_t+\alpha_t( r_{t+1}+\gamma {\color{orange}{\hat{q}(s_{t+1},a_{t+1},w_t)}} - {\color{orange}{\hat{q}(s_t,a_t,w_t)}} ) {\color{orange}{\nabla_{w}\hat{q}(s_t,a_t,w_t)}} \end{align*}$$ 對比橘色的部分, 可以看到跟 state value 方法對比只是把 $\hat{v}$ 換成 $\hat{q}$ 而已

Q-learning with function approximation

同樣的 Q-learning with function approximation 的算法公式如下:
$$\begin{align*} w_{t+1}=w_t+\alpha_t \left[ r_{t+1}+\gamma {\color{orange}{\max_{a\in\mathcal{A}(s_{t+1})}\hat{q}(s_{t+1},a,w_t)}} - \hat{q}(s_t,a_t,w_t) \right] \nabla_{w}\hat{q}(s_t,a_t,w_t) \end{align*}$$ 基本上只是 TD target 改成 Q-learning 的 TD target (可以去回顧前面的整理)
上圖的 pseudocode 是 on-policy (behavior 策略跟 target 策略相同), 所以還是使用 $\epsilon$-greedy 更新目標策略以避免 exploring starts 缺點
但別忘了, Q-learning 實際上是直接求解 BOE, 因此可以直接計算最佳策略
其中一個最大的好處是 Q-learning 是 off-policy 的, 所以可以不用 policy improvement (or called update policy) 這一步
Off-policy 的 Q-learning 會在下面用 Deep Q-learning (DQN) 給出

Deep Q-learning or Deep Q-network (DQN)

Deep Q-learning or DQN 可以視為 Q-learning (function approximation) 的推廣作法, 數學(優化)目標函式為:
$$\begin{align*} J(w)=\mathbb{E}\left[\left( \underbrace{\color{orange}{R+\gamma\max_{a\in\mathcal{A}(S')}\hat{q}(S',a,w)}}_{\text{TD Target}} - \underbrace{\hat{q}(S,A,w)}_{\text{Predicted Q-value}} \right)^2\right] \end{align*}$$ DQN 的目標函式跟 Q-learning (tabular) 的 BOE 等價, 都是直接求解 BOE [證明]
實務上 DQN 使用了兩個 NN models, 稱 main network ${\color{orange}{\hat{q}(s,a,w)}}$ 和 target network ${\color{green}{\hat{q}(s,a,w_T)}}$:
$$\begin{align*} J(w)=\mathbb{E}\left[\left( R+\gamma\max_{a\in\mathcal{A}(S')} {\color{green}{\hat{q}(S',a,w_T)}} - {\color{orange}{\hat{q}(S,A,w)}} \right)^2\right] \end{align*}$$ 然後 update main NN ${\color{orange}{\hat{q}(s,a,w)}}$ 時 target network ${\color{green}{\hat{q}(s,a,w_T)}}$ 視為常數不動, 所以 main network 的 gradient 很好計算
然後幾次 iteration 後, 把更新後的 main NN ${\color{orange}{\hat{q}(s,a,w)}}$ copy 過去給 target network ${\color{green}{\hat{q}(s,a,w_T)}}$, DQN 就是透過這樣的技巧很成功的把 DNN 引入到 RL 中
更多細節, 譬如這樣做的好處, 以及 mini-batch 採用 uniform distribution 抓取 examples 等, 請參考 Week8 筆記
DQN off-policy pseudocode:

[Ch9]: Policy Gradient Methods

讓 actions 不只限於 tabular form, 也可以是 continous form, 即 $\pi(a,\theta)$, 其中 $\theta$ 為參數.
以前 tabular 形式的 optimal policy 可以直接求解 BOE 得到. 且明確知道 optimal policy 代表該 policy 在任何 state 都能得到最大的 value.
但什麼是 optimal 的 continous policy 就需要透過一些 metrics 來定義優劣.
藉由這些 metrics 用 SGD 來優化找出最佳 policy, 這種方法稱 policy gradient method.
Metrics 有兩種常見的定義方式

  • [Metric 1] Average state value $\bar{v}_\pi$: 每一個 state 的 value $v_\pi(s)$ 根據 state 分布 $d(s)$ 做個平均, 分兩種情況
    • $d(s)$ 跟 policy $\pi$ 無關: 用 $\bar{v}_\pi^0$ 和 $d_0$ 來表示. 例如 $d(s)=1/|\mathcal{S}|$ 是一個 uniform. 或當我們只關心某一個 state 的話, $d_0$ 就是一個 one-hot vector.
    • $d(s)$ 跟 policy $\pi$ 有關: 通常設定為 stationary distributino $d_\pi(s)$, 其滿足 $d_\pi=P_\pi d_\pi$, 其中 $P_\pi$ 為狀態轉移矩陣.
  • [Metric 2] Average one-step reward $\bar{r}_\pi$: 目前狀態是 $s$ 的情況下, 走一步的條件下得到的平均 immediate rewards
    • 其中 $r_\pi(s)=\sum_{a\in\mathcal{A}}\pi(a|s,\theta){\sum_r}rp(r|s,a)$, 則 $\bar{r}_\pi=\sum_{s\in\mathcal{S}}d_\pi(s)r_\pi(s)$.

以下有三種等價的 expressions 都很重要 (詳細參考 Week9)

Metric Expression 1 Expression 2 Expression 3
$\bar{v}_\pi$ $\sum_{s\in\mathcal{S}}d(s)v_\pi(s)$ $\mathbb{E}_{S\sim d}[v_\pi(S)]$ $\lim_{n\rightarrow\infty}\mathbb{E}\left[\sum_{t=0}^n{\gamma^t R_{t+1}}\right]$
$\bar{r}_\pi$ $\sum_{s\in\mathcal{S}}d_\pi(s)r_\pi(s)$ $\mathbb{E}_{S\sim d_\pi}[r_\pi(S)]$ $\lim_{n\rightarrow\infty}\frac{1}{n}\mathbb{E}\left[\sum_{t=0}^{n-1}{R_{t+1}}\right]$

當使用 stationary $d_\pi$ 時, 兩者等價 ${\color{orange}{\bar{r}_\pi=(1-\gamma)\bar{v}_\pi}}$.
最大化採用 gradient ascent, 但 gradient 的計算非常複雜, 還要考慮不同 cases 的情況, e.g. discounted or undiscounted cases, 不同 metrics $\bar{v}_\pi$, $\bar{v}_\pi^0$, $\bar{r}_\pi$.
因此課程上老師只列出 gradient 通用的形式:
$$\begin{align*} {\color{orange}{\nabla_\theta J(\theta)=\sum_{s\in\mathcal{S}}\eta(s)\sum_{a\in\mathcal{A}}\nabla_\theta\pi(a|s,\theta)q_\pi(s,a)}} \\ {\color{orange}{=\mathbb{E}_{S\sim\eta,A\sim\pi(S,\theta)}\left[\nabla_\theta\ln\pi(A|S,\theta)q_\pi(S,A)\right]}} \end{align*}$$ 其中 $J(\theta)$ 可以是 $\bar{v}_\pi$, $\bar{v}_\pi^0$, $\bar{r}_\pi$, 會導致 $\eta$ 會對應到不同的 state distributions 定義或變成 weightings, 同時 “$=$” 也有可能變成 “$\approx$”.
總結如下:
$$\begin{align*} \nabla_\theta\bar{r}_\pi\approx \sum_sd_\pi(s)\sum_a \nabla_\theta\pi(a|s,\theta)q_\pi(s,a),\\ \nabla_\theta\bar{v}_\pi=\frac{1}{1-\gamma}\nabla_\theta\bar{r}_\pi,\\ \nabla_\theta\bar{v}_\pi^0=\sum_s\rho_\pi(s)\sum_a\nabla_\theta\pi(a|s,\theta)q_\pi(s,a) \end{align*}$$ 其中 $\rho_\pi(s)$ [詳細定義] 為在 policy $\pi$ 下的 discounted total probability of transitioning from $s'$ to $s$.

Jia-Bin Huang 這支影片 [YouTube] 推導了 $\nabla_\theta\bar{r}_\pi$, 我覺得滿清楚的, 推薦看一下

所以 (Stochastic) Gradient Ascent (GA/SGA) 流程:
$$\begin{align*} \theta_{t+1}=\theta_t + \alpha\nabla_\theta J(\theta_t) \\ \text{(GA)}\quad=\theta_t + \alpha\mathbb{E}\left[\nabla_\theta\ln\pi(A|S,\theta_t)q_\pi(S,A)\right] \\ \text{(SGA)}\quad=\theta_t + \alpha\nabla_\theta\ln\pi(a_t|s_t,\theta_t)q_{\color{red}{\pi}}(s_t,a_t) \end{align*}$$ 注意到我們無法得知 ground truth 的 $q_{\color{red}{\pi}}(s_t,a_t)$, 因此直接用估計的 $q_{\color{red}{t}}(s_t,a_t)$ 替代
估計的 $q_{\color{red}{t}}(s_t,a_t)$ 可以用多種方法, 常見的有使用 MC (Monte Carlo) 方法和 TD 方法兩種 (TD 的方法為下一章 Actor-Critic)
其中 MC 方法的 policy gradient 又稱為 REINFORCE 方法, 其估計的 $q_{\color{red}{t}}(s_t,a_t)$ 使用 $q_t(s_t,a_t)=\sum_{k=t+1}^T\gamma^{k-t-1}r_k$:
因此 REINFORCE 演算法為
這算是最早且最簡單的 policy gradient 方法
注意到 GA (13) 採樣的時候我們是 follow $S\sim\eta$, $A\sim\pi(S,\theta)$. $S\sim\eta$ 是一個 long run 的 distribution 後的採樣, 通常人們不太關心
主要是 $A\sim\pi(S,\theta)$, 這使得 $a_t$ 必須從 $\pi(S,\theta_t)$ 採樣出來, 也因此更新的 policy 同時也是採樣時候的 policy, 表示 REINFORCE 是 on-policy 算法.

[Ch10]: Actor-Critic Methods

QAC (Q-function actor-critic)

上面的 MC policy gradient (REINFORCE) 算法, 把 value update 的地方採用 action value with function approximation 的方法就得到最簡單的 QAC 了
注意到改成 TD 變成有 incremental update 的好處, 不用像 MC 一樣等到一條 trajectory 採樣完才能做.

On-policy A2C (Advantage actor-critic)

其實 A2C 就是使用: https://bobondemon.github.io/2025/06/04/REINFORCE-estimator/ 提到的 baseline + control-variates 技巧, 去改進 QAC 的結果.
重複一次 policy gradient 的公式 $\nabla_\theta J(\theta_t)=\mathbb{E}_{S\sim\eta,A\sim\pi}\left[\nabla_\theta\ln\pi(A|S,\theta_t)q_\pi(S,A)\right]$.
SGA 每次採樣出一個 $\nabla_\theta\ln\pi(A|S,\theta_t)q_\pi(S,A)$ 來更新, 觀察到如果加上一個與 $\mathcal{A}$ 無關的變數 $b(S)$ 對於計算期望值不會有任何影響
$$\begin{align*} X\doteq\nabla_\theta\ln\pi(A|S,\theta_t)(q_\pi(S,A)-{\color{orange}{b(S)}}) \\ \Longrightarrow \mathbb{E}_{S\sim\eta,A\sim\pi}[X]=\nabla_\theta J(\theta_t) \end{align*}$$ 但是 $Var(X)$ 仍會被 $b(S)$ 影響, 即 $b(S)$ 不同則算出來的 $Var(X)$ 不同, 因此目標就是找出一個最佳的 baseline $b(S)$ 使得 $Var(X)$ 最小
這樣做 SGA 採樣出來的 sample 之間 variance 就變小, 收斂快又穩定. 而理論上最佳解為:
$$\begin{align*} b^\ast(s)=\frac{\mathbb{E}_{A\sim\pi}[ {\color{orange}{\|\nabla_\theta\ln\pi(A|s,\theta_t)\|^2}} q_\pi(s,A) ]} {\mathbb{E}_{A\sim\pi}[ {\color{orange}{\|\nabla_\theta\ln\pi(A|s,\theta_t)\|^2}}]} \end{align*}$$ 雖然這是最佳解, 但比較複雜通常不用, 我們直接把橘色的權重拔掉變成 ${\color{orange}{b(s)}}=\mathbb{E}_{A\sim\pi}[q_\pi(s,A)]{\color{orange}{=v_\pi(s)}}$. Baseline $b(s)$ 就設定成 state value $v(s)$ 即可!
加上 basline term 的 policy gradient 變成:
$$\begin{align*} {\color{orange}{\nabla_\theta J(\theta_t)}} = \mathbb{E}_{S\sim\eta,A\sim\pi} \left[\nabla_\theta\ln\pi(A|S,\theta_t) {\color{orange}{\delta_\pi(S,A)}}\right] \\ {\color{orange}{\delta_\pi(S,A)\doteq q_\pi(S,A)-{v_\pi(S)}}} \end{align*}$$ $\delta_\pi(S,A)$ 稱為 advantage function.
所以之前的 policy gradient 其 gradient ascent 公式改為:
$$\begin{align*} \theta_{t+1}=\theta_t + \alpha\nabla_\theta J(\theta_t) \\ \text{(GA)}\quad=\theta_t + \alpha\mathbb{E}\left[\nabla_\theta\ln\pi(A|S,\theta_t){\color{orange}{\delta_\pi(S,A)}}\right] \\ \text{(SGA)}\quad=\theta_t + \alpha\nabla_\theta\ln\pi(a_t|s_t,\theta_t) {\color{orange}{\delta_{\color{red}{t}}(s_t,a_t)}} \end{align*}$$ 從 GA 到 SGA 我們也把無法得知的 $\delta_\pi(s_t,a_t)$ 用估計的 $\delta_t(s_t,a_t)$ 來替代
其中 $\delta_t(s_t,a_t)$ 可以用 temporal difference 的想法來逼近:
$$\begin{align*} \delta_t(s_t,a_t)\doteq {\color{orange}{q_t(s_t,a_t)}}-v_t(s_t) \approx {\color{orange}{r_{t+1}+\gamma v_t(s_{t+1})}} -v_t(s_t) \end{align*}$$ 這帶來的好處是只需要用一個 NN 學 $v_t$ 即可.

Off-policy A2C (Advantage actor-critic)

再結合 Important Sampling (IS) 將 on-policy 的 A2C 變成 off-policy, 則 policy gradient 公式變成:
$$\begin{align*} \nabla_\theta J(\theta_t)=\mathbb{E}_{S\sim\eta,A\sim{\color{orange}{\pi}}} \left[\nabla_\theta\ln\pi(A|S,\theta_t) \delta_\pi(S,A)\right] \\ =\mathbb{E}_{S\sim\eta,A\sim{\color{orange}{\beta}}} \left[ {\color{orange}{\frac{\pi(A|S,\theta)}{\beta(A|S)}}} \nabla_\theta\ln\pi(A|S,\theta_t) \delta_\pi(S,A) \right] \\ =\mathbb{E}_{S\sim\eta,A\sim{\color{orange}{\beta}}} \left[ {\color{orange}{\frac{\delta_\pi(S,A)}{\beta(A|S)}}} \nabla_\theta\pi(A|S,\theta_t) \right] \end{align*}$$ $\beta$ 是 behavior policy, user 定義地所以可以計算 $\beta(A|S)$. 因此
$$\begin{align*} \theta_{t+1}=\theta_t + \alpha\nabla_\theta J(\theta_t) \\ \text{(GA)}\quad=\theta_t + \alpha\mathbb{E}_{S\sim\eta,A\sim{\color{orange}{\beta}}} \left[ {\color{orange}{\frac{\delta_\pi(S,A)}{\beta(A|S)}}} \nabla_\theta\pi(A|S,\theta_t) \right] \\ \text{(SGA)}\quad=\theta_t + \alpha {\color{orange}{\frac{\delta_{\color{red}t}(s_t,a_t)}{\beta(a_t|s_t)}}} \nabla_\theta\pi(a_t|s_t,\theta_t) \end{align*}$$ 注意到從 GA 變成 SGA 的時候, 我們也將無法得知的 advantage function $\delta_\pi$ 替還成目前正在估計的 $\delta_t$ 了. 因此 important weight $\delta_t/\beta$ 很容易計算.

💡 用 PyTorch 的 auto-diff 實作的時候不會自己刻 gradient, 我們只需要定義好等價的 loss function
而對應給 PyTorch 的 loss function $L(\theta)$ 為: (同樣也把 advantage function $\delta_\pi$ 替還成還在估計的 $\delta_t$)
$$\begin{align*} L(\theta)=-J(\theta)=-\mathbb{E}_{S\sim\eta,A\sim{\color{orange}{\beta}}}\left[\frac{\pi(A|S)}{\beta(A|S)}\delta_{\color{red}t}(S,A)\right]\end{align*}$$ (用 log derivative trick 很容易驗證, or see here) 這個目標函式通常稱為 surrogate objective 也才是最後 NN 要做 training 的 loss.

結論, A2C 的 off-policy psuedo code 如下:

注意到這邊我們對 state value $v_t$ 採用 function approximation 方法, 參考 Ch8 這裡. 但是要再加上 importance weight 修正.