DPO 捨棄 RLHF 中笨重的 reward model, 並將 RL 問題直接轉換成對好壞兩個 responses 的 supervised training. [圖片產生自 ChatGPT]
Pre-trained model 經過 SFT (Supervised Fine-Tuning) 再經過 RLHF (Reinforcement Learning from Human Feedback) 的這一套組合拳在 2023 年堪稱顯學
網路上甚至產生了一個很有名的修格斯(Shoggoth)怪物梗圖. (wiki: 形態無定的原生質生物,是克蘇魯神話中最駭人的存在之一)

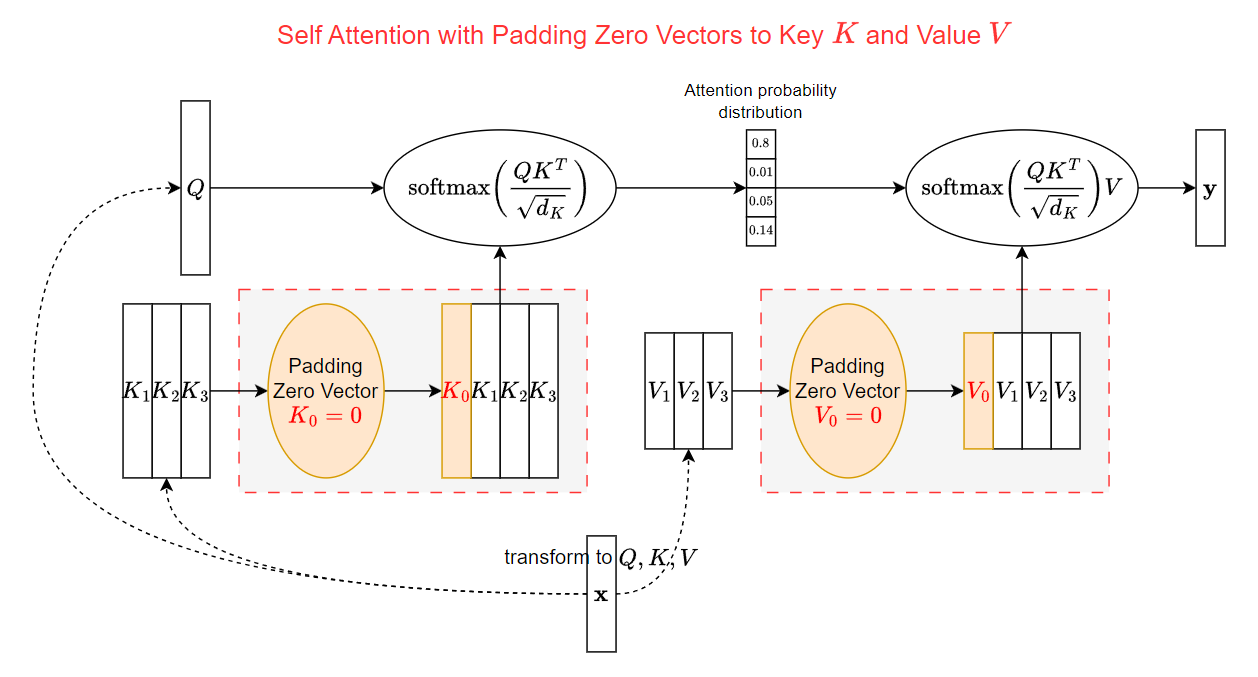 初次看到可能會很疑惑, 為啥要多 padding zero vectors? 本文就來解釋一下原因.
初次看到可能會很疑惑, 為啥要多 padding zero vectors? 本文就來解釋一下原因.