為何三個臭皮匠會勝過一個諸葛亮?
在 ML 中有一類的演算法稱為 Aggregation Methods,這方法的運作方式其實我們可能從小就接觸到了。有沒有遇過一種情況就是,當一群人遇到一個不知道最好答案的時候,最直接的方式就是大家的答案取平均。
聽起來很直覺,但心裡老覺得怪怪的,因為根本不知道到底可不可靠。
Aggregation methods 就是這樣的運作模式,這邊就給個結論,它很可靠!
以下的推導出自於林軒田教授的講義,這裡用自己的理解方式重新表達,主要作筆記用
開頭還是給先定義清楚一些 terms,對於理解式子才不會混淆
定義在先
- Input: \(x \in X\)
- 正確答案: \(f(x)\)
- 臭皮匠: \(g_t(x),t=1,2,…\)
- 臭皮匠們的決策結果: \(G(x)=avg_t(g_t(x))\)
- 衡量方法 \(g\) 的錯誤率: \( Error(g)=E_x[(g(x)-f(x))^2]\)
這邊要特別說的是衡量一個方法 \(g\) 的錯誤率,是針對所有的 input \(x\),也就是針對 \(X\) domain 來算期望平方誤差
運算簡單但有點神奇的推導
我們先針對 一個固定的 x,來看看臭皮匠們統合的意見是否真的會得到較好的結果,由於input已經固定,所以下面會忽略 x 的 term
首先是 “臭皮匠們各自的平方錯誤率” 的平均值
$$avg_t((g_t-f)^2)$$
將平方拆開後得
$$=avg_t(g_t^2-2g_tf+f^2)$$
將 avg 移入並用 G=avg(gt) 定義得到
$$=avg_t(g_t^2)-2Gf+f^2$$
再做如下的簡單代數運算
$$=avg_t(g_t^2)-G^2+(G-f)^2 \\
=avg_t(g_t^2)-2G^2+G^2+(G-f)^2 \\
=avg_t(g_t^2-2g_tG+G^2)+(G-f)^2 \\
=avg_t((g_t-G)^2)+(G-f)^2$$目前為止是針對 一個特定的輸入 x,而我們需要知道的是對 整個 domain X 的錯誤率
因此真正要計算的是這個目標錯誤率
$$avg_t(Error(g_t))=avg_t(E_x[(g_t(x)-f(x))^2])$$
將 Expection for all x 代入進去剛剛上面針對一個 x 的結果,得到如下式子
\begin{eqnarray}=avg_t(E_x[(g_t(x)-G(x))^2])+E_x[(G(x)-f(x))^2] \\
=avg_t(E_x[(g_t(x)-G(x))^2])+Error(G) \\
\geq Error(G) \end{eqnarray}
怎麼解釋?
重複一下最後的重要式子:
$$avg_t(Error(g_t)) = avg_t(E_x[(g_t(x)-G(x))^2])+Error(G) \\
\geq Error(G)$$
最直接的結論就是: “統合出來的結果”的錯誤率 會比 “各自決定”的平均錯誤率 還要低
可以看到針對 一組固定 的臭皮匠們 \({g_t}\),不等式左邊 \(avg_t(Error(g_t))\) 是固定值,因此若要找一個統合大家意見的方法 \(G\),而該方法有最小的錯誤率 (最小化 \(Error(G)\) ),很明顯就是要最大化 \(avg_t(E_x(g_t-G)^2)\),而此最大化的結果 就是 \(G\) 是 \({g_t}\) 的平均值(uniform blending),符合我們一開始說的最直覺的策略!
另一方面,如果我們選到兩組 set \({g_t}\) and \({h_t}\) 他們的 Error 相同: \(avg_t(Error(g_t))= avg_t(Error(h_t))\) ,那我們當然是要選擇意見最不同的那一組臭皮匠們,這是因為意見愈不同代表 \(avg_t(E_x(g_t-G)^2)\) 愈大,因而導致 \(Error(G)\) 會愈小。
小結
剛剛上面這個結論就很有趣,意見遇不同的話,統合起來的效果愈好,也就是你我之間的意見有很大的分歧時,這代表是好事!
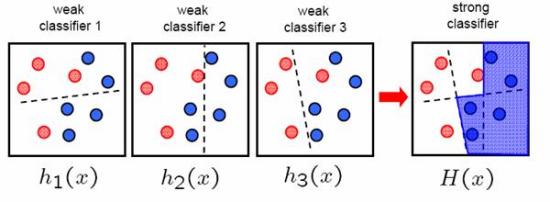
事實上 Adaboost 就是採取這麼一個策略,每一次的 iteration 會選擇跟上次統合完的結果意見差最多那一位臭皮匠進來,有機會再補上 Adaboost,這是我很喜歡的一種 ML 演算法。
而這邊還可以引出一個方法, Bootstrap. Bootstrap aggregation方法很簡單。
對我們的dataset每一次重新resampling (e.g. 取N’筆,每次取的data都再放回去,因此data可以重複。可重複這點造成dataset的point具有weight的性質,這在adaboost每一次iteration的re-weighting有同樣意思) 這個叫做bootstrap,針對該次的data算出我們的weak learner gt,iterate很多次後,把每一次的gt做uniform blending。
我認為 aggregation methods 就算放到現在的 Deep Learning 火熱的時代還是相當有用的,除了本身這些方法如 adaboost 好用之外,其概念也相當有用,例如 Deep Learning 的 dropout 事實上可以用 bootstrap 來解釋 (有機會再補上資料)