Open.ai 這張表達 generative modeling 的意思很清楚,忍不住就借用了。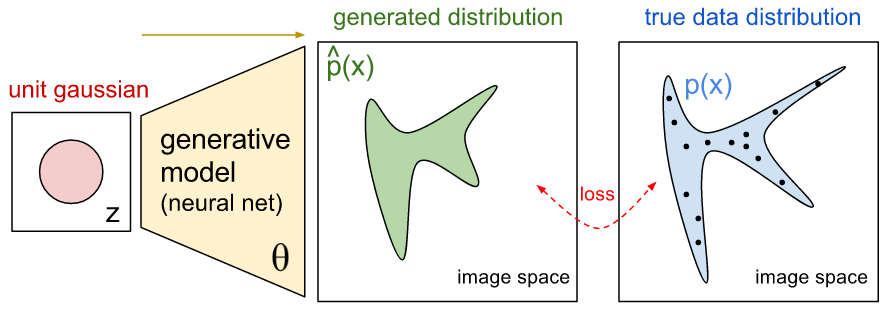
筆者才疏學淺,如有錯誤,還請指正
Generative Adversarial Nets 提出了一個 NN 的 generative modeling 方法,在這之前,NN 要成為 p.d.f. 必須依賴於 sigmoid activation 的 Restricted Boltzmann Machines (RBM) 結構。例如 Deep Belief Net,整個 network 才會是一個 p.d.f.。然而學習這樣的一個 p.d.f. 必須使用 Contrastive Divergence 的 MCMC 方法, model 訓練完後要產生 sample 時也還是必須依賴 MCMC。加上在實用上,偏偏 sigmoid 很多時候效果不如 ReLu, maxout 等,例如 sigmoid 有嚴重的 gradient vanish problem。這使得 NN 在 generative modeling 又或是 unsupervised learning 上一直困難重重。
GAN 一出立即打破這個難堪的限制 ! 怎麼說呢? GAN 捨棄能夠明確表達出 p.d.f.的作法,寫不出明確的 p.d.f. 一點也沒關係,只要能生成 夠真的sample點,並且sample的機率跟training data一樣就好
然而 GAN 在實作上卻會遇上一些困難,例如生成的 samples 多樣性不足,訓練流程/架構 和 hyper-parameters 需要小心選擇,無法明確知道訓練的收斂狀況,這些問題等下會說明。
本篇的主角 (事實上下一篇才會登場) Wasserstein GAN (WGAN),從本質上探討 GAN 目標函式中使用的 distance measure,進而根本地解決上述三個問題,這大大降低了 generative modeling 訓練難度 !
我們還是來談談 GAN 怎麼一回事先吧。
Generative Adversarial Nets
GAN 使用一個 two-player minimax gaming 策略。先用直觀說,我們有一個 生成器 \(G\),用來生成夠真的 sample,另外還有一個 鑑別器 \(D\),用來分辨 sample 究竟是真實資料 (training data) 來的呢,還是假的 (\(G\)產生的)。
當這兩個模型互相競爭到一個平衡點的時候,也就是 \(G\) 能夠產生到 \(D\) 分辨不出真假的 sample,我們的生成器 \(G\) 就鍊成了。
而 GAN 作者厲害的地方就在於
一: 將這兩個model的競爭規則轉換成一個最佳化問題
二: 並且證明,當達到賽局的平衡點時(達到最佳解),生成器就鍊成 (可以完美表示 training data 的 pdf,並且可sampling)
我們還是必須把上述策略嚴謹的表達出來 (寫成最佳化問題),並證明當達到最佳化問題的最佳解時,就剛好完成生成器的鍊成。
Two-player Minimax Game
原則上我們希望鑑別器 \(D\) 能分辨出真假 sample,因此 \(D(x)\) 很自然地可以表示為 sample \(x\) 為真的機率
另外生成器 \(G\) 則是負責產生假 sample,也可以很自然地表達為 \(G(z)\),其中 \(z\) 為 latent variables,且我們可以假設該 latent variables \(z\) follow 一個 prior distribution \(p_z(z)\)。
我們希望 \(D(x)\) 對來自於真實資料的 samples 能夠盡量大,而對來自於 \(G\) 產生的要盡量小,因此對於鑑別器來說,它的目標函式可定義為如下:
$$\begin{align} Maximize: E_{x \sim p_{data}(x)} [\log D(x)] + E_{z \sim p_z(z)}[\log (1-D(G(z)))] \end{align}$$另一方面,我們希望 \(G\) 能夠強到讓 \(D\) 無法分辨真偽,因此生成器的目標函式為:
$$\begin{align} Minimize: E_{z \sim p_z(z)}[\log (1-D(G(z)))] \end{align}$$結合上述兩個目標函式就是如下的 minmax problem了
$$\begin{align} \min_G{ \max_D{V(D,G)} } = E_{x \sim p_{data}(x)} [\log D(x)] + E_{z \sim p_z(z)}[\log (1-D(G(z)))] \end{align}$$這邊作者很漂亮地給出了上述問題的理論證明。證明了兩件事情:
上述最佳化問題 (式(3)) 達到 global optimum 時, \( p_g = p_d \)。 (生成器產生出來的 pdf 會等於真實資料的 pdf,因此生成器鍊成!)
使用如下的演算法可以找到 global optimum
接下來我們只討論第一個事情的證明,因為這關係到 GAN 的弱點,也就是 WGAN 要解決的問題根源!
證明 Global optimum 發生時,鍊成生成器
大方向是這樣的
A. 假如給定 \(G\),我們都可以找到一個相對應的 \(D_G^*\) 最佳化鑑別器的目標函式 (1)。
B. 改寫原來的目標函式 \(V(G,D)\),改寫後只跟 \(G\) 有關,我們定義為 \(C(G)\),這是因為對於每一個 \(G\) 我們已經配給它相對應的 \(D_G^*\) 了,接著證明最佳解只發生在 \( p_g = p_d \) 的情況。
步驟 A:
$$V(G,D)=\int_{x}{p_d(x)\log(D(x))dx}+\int_{z}{p_z(z)\log(1-D(g(z)))dz} \\ =\int_x[p_d(x)\log(D(x))+p_g(x)\log(1-D(x))]dx$$而一個 function \(f(x)=a\log (y)+b\log (1-y)\) 的最佳解為 \(y=\frac{a}{a+b}\)
因此我們得到 \( D_G^*(x) = \frac{p_d(x)}{p_d(x)+p_g(x)} \)步驟 B:
$$\begin{align*} & C(G)=\max_{D}V(G,D) \\ & =E_{x \sim p_d}[\log D_G^*(x)]+E_{z \sim p_z}[\log(1-D_G^*(G(z)))] \\ & =E_{x \sim p_d}[\log D_G^*(x)]+E_{x \sim p_g}[\log(1-D_G^*(x))] \\ & =E_{x \sim p_d}[\log{\frac{p_d(x)}{p_d(x)+p_g(x)}}]+E_{x \sim p_g}[\log{\frac{p_g(x)}{p_d(x)+p_g(x)}}] \end{align*}$$然後我們特別觀察如果 \(p_g = p_d\),上式會
$$\begin{align} =E_{x \sim p_d}[-\log 2]+E_{x \sim p_g}[-\log 2]=-\log4 \end{align}$$重新改寫一下 \(C(G)\) 如下
$$\begin{align} C(G)=-\log4+KL(p_d\vert\frac{p_d+p_g}{2})+KL(p_g\vert\frac{p_d+p_g}{2}) \\ =-\log4+2JSD(p_d \vert p_g) \end{align}$$馬上觀察到 \(JSD\geq0\) 和 \(JSD=0 \Leftrightarrow p_g = p_d \)
這表示 \(C(G)\) 最佳值為 \(-\log4\),且我們已知當 \(p_g = p_d\) 時達到最佳值 (式(4)),因此為最佳解
結論整個 GAN 的流程:
我們基於一個生成器 \(G\) 去最佳化 \(D\) 得到 \(D_G^*\),接著要繼續最佳化生成器的時候,問題從目標函式 (3) 變成等價於要最佳化一個 JSD 的問題 (式(5))。
藉由最佳化 JSD 問題,得到新的 \(G\),然後重複上面步驟,最後達到式(3)的最佳解,而我們可以保證此時生成器鍊成, \(p_g = p_d\)。
問題出在哪? 問題就出在最佳化一個 JSD 的問題上面 !
JSD 有什麼問題?
我們通過最佳化 JSD,而將 \(p_g\) 逐漸拉向 \(p_d\)。但是 JSD 有兩個主要的問題:
A. 在 實際狀況 下,無法給初連續的距離值,導致 gradient 大部分都是 0,因而非常難以訓練
B. 產生的樣本多樣性不足,collapse mode。
這邊要解釋一下 實際狀況 是什麼意思。一般來說,真實資料我們都會用非常高的維度去表示,然而資料的變化通常只被少數幾種變因所控制,也就是只存在高維空間中的 local manifold。
例如一個 swiss roll 雖然是在 3 維空間中,但它是在一個 2 維的 manifold 空間裡。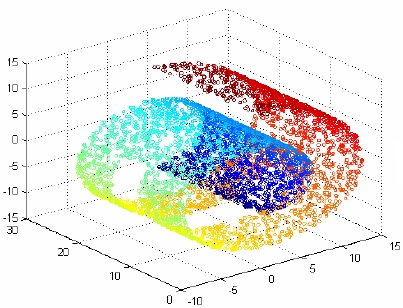
這樣會造成一個問題就是, \(p_d\) 和 \(p_g\),不會有交集,又或者交集處的集合測度為0!
這樣的情況在JSD衡量兩個機率分布的時候會悲劇。作者給出了下面一個簡單易懂的例子:
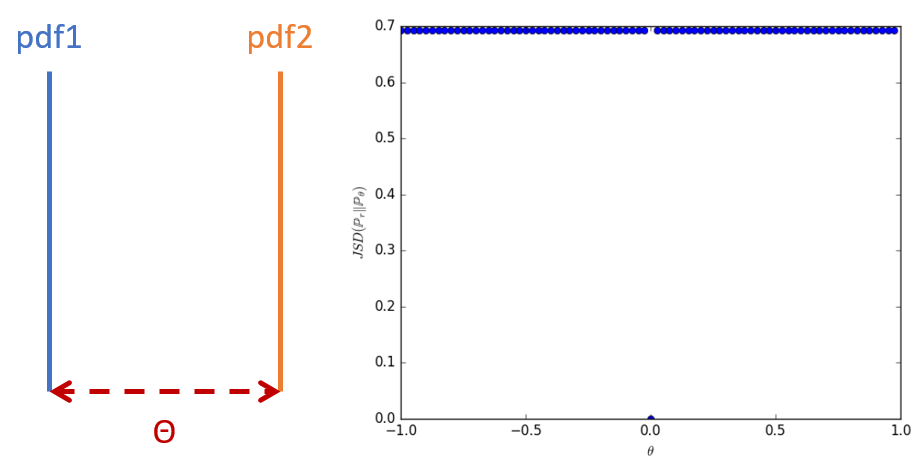
兩個機率分布都是在一個 1 維的 manifold 直線上,x 軸的距離維 \(\theta\),此時的 JSD 值為右圖所示,全部都是 \(\log2\),除了在 \(\theta\) 那點的值是 0 (pdf完全重疊)。
這樣計算出的 Gradients 幾乎都是 0,這也就是為什麼 GAN 很難訓練的原因。
這問題在 WGAN 之前還是有人提出解決的方法,不過就很偏工程思考: 加入 noise 使得兩個機率分部有不可忽略的重疊。因此讓 GAN 先動起來,動起來之後,再慢慢地把 noise 程度下降。
這是聰明工程師的厲害辦法! 但終歸來說還是治標。真正的治本方法,必須要替換掉 JSD 這樣的量測函式才可以。
本篇鋪梗結束 (這梗也太長了)。下篇終於輪到主角登場, WGAN 的 W !
