
Udacity term2 (Sensor Fusion, Localization, and Control) 的第一個 Project 就是用 KF and EKF 將 Lidar and Radar 的資訊做 fusion 並且可以 tracking。由於 KF/EKF 的數學符號很多,因此想筆記一下方便日後回想,所以主要以我自己看的角度,可能有些地方會沒有明確說明。本篇的筆記來源是
- 這裡,這篇真的講的超棒的,清楚易懂! 非常建議直接去看!
- Udacity 課程內容
若要實作所有的計算流程不管理論的話,可直接跳到 “7. 總結 Lidar and Radar Fusion”。
State Space Model
這是整個 KF/EKF 的模型假設,寫出來如下:
$$\begin{align} x_k = F_kx_{k-1}+\nu_k \\ z_k = H_kx_k+\omega_k \end{align}$$\(x_k\) 是在時間點 \(t\) 的 states,也是我們希望能夠估計出來的(但是無法直接觀察到)。而 states 滿足 線性的一次遞迴 關係,也就是式子(1)。 \(\nu_k\sim\mathcal{N}(0,Q_k)\) 是 state nose。
\(z_k\) 是在時間點 \(t\) 的 observations,透過 \(H_k\) 將 states 轉換到 observations。 \(\omega_k\sim\mathcal{N}(0,R_k)\) 是 sensor noise,而 \(R_k\) 基本上會由製造廠商提供。基本上兩個 noises 都跟所有人都 independent。
Prediction Stage
整個 KF/EKF 都是基於 Gaussian distribution。因此假設我們有 \(k-1\) 時間點的 state 估計,所以我們知道 \(x_{k}\sim\mathcal{N}(\hat{x}_k,P_k)\) 會變成如下的一個 Gaussian:
$$\begin{align} \hat{x}_{k}=F_k\hat{x}_{k-1} \\ P_k = F_kP_{k-1}F_k^T+Q_k \end{align}$$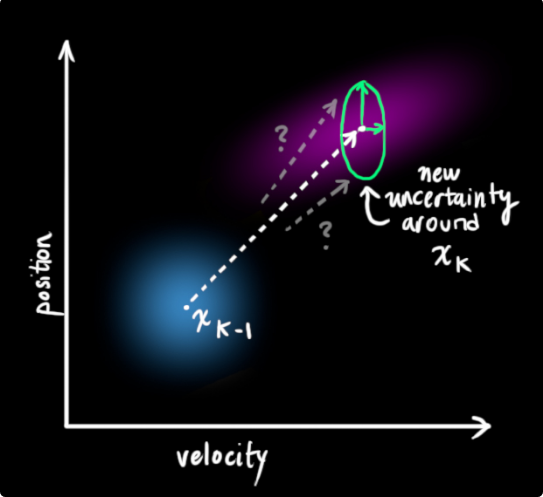
式(3)and(4)即為 Prediction Stage。
又因為我們知道 observation 跟 state 之間的關係為透過 \(H_k\) 轉換,在完全沒有 sensor noise 情況下,所以可以得知 prediction 的觀察值為:
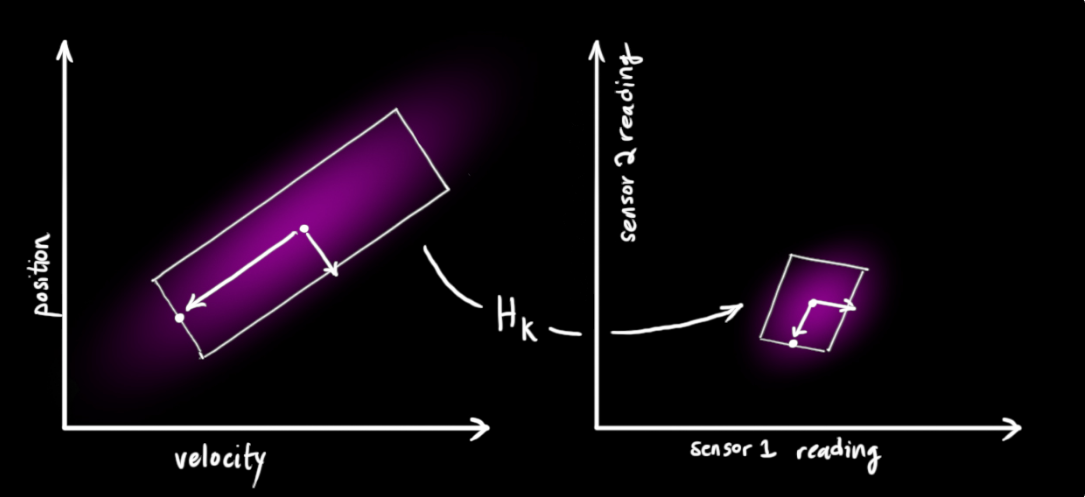
Update Stage
我們令實際上的觀察值為 \(z_k\sim\mathcal{N}(\vec{z}_k,R_k)\),將觀察值的 Gaussian 和 predict 的 Gaussian 畫出如下:
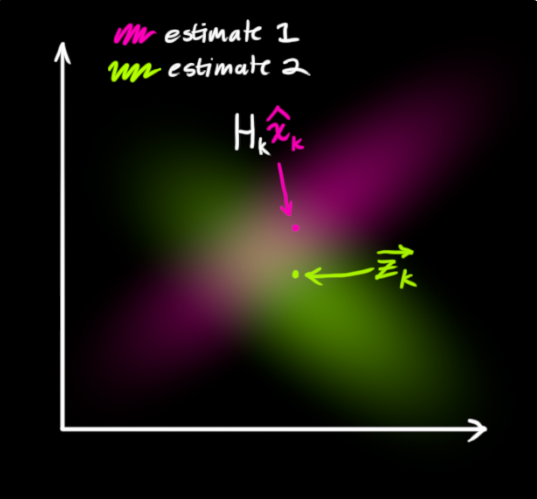
而將兩個 Gaussian pdfs 相乘的話:
$$\begin{align}
\mathcal{N}(x,\mu_0,\Sigma_0)\cdot\mathcal{N}(x,\mu_1,\Sigma_1)=\mathcal{N}(x,\mu',\Sigma') \\
\end{align}$$
仍然會得到另一個 Gaussian:
$$\begin{align}
K=\Sigma_0(\Sigma_0+\Sigma_1)^{-1} \\
\mu'=\mu_0+K(\mu_1-\mu_0) \\
\Sigma'=\Sigma_0-K\Sigma_0
\end{align}$$
\(K\) 稱為 Kalman Gain。由式(10)可知,update 後的 covariance matrix 會愈來愈小,表示我們對於 prediction 的觀察值會愈來愈確定。另外由(9)可知,Kalman Gain 控制著要相信哪邊多一點。
把估測的觀察值 pdf 和實際觀察值的 pdf,即 \(z_k\sim\mathcal{N}(\vec{z}_k,R_k)\) 和式(5)兩個 pdfs 代入到式 (8)~(10) 得到如下:
把 (11)~(13) 開頭的 \(H_k\) 去掉,並且把 (12) and (13) 結尾的 \(H_k^T\) 去掉變成
$$\begin{align}
\hat{x}_k'=\hat{x}_k+K(\vec{z}_k-H_k\hat{x}_k) \\
P_k'=P_k-KH_kP_k \\
K=P_kH_k^T(H_kP_kH_k^T+R_k)^{-1}
\end{align}$$
(14)~(16)就是 KF 的 Update Stage! 新的 states 估計值就被我們得到,然後這個值就可以被當成下一次 loop 的初始值。
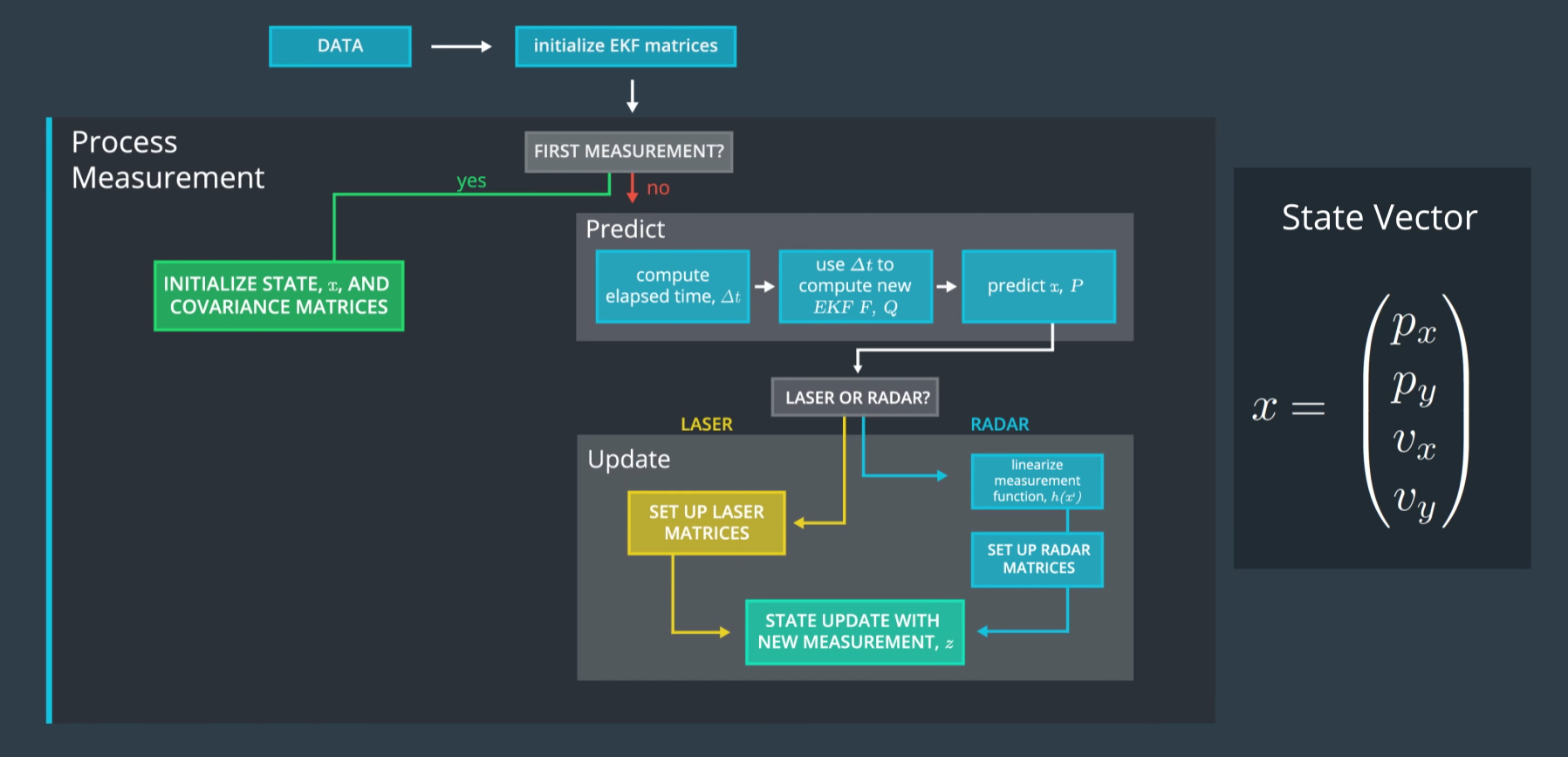
KF Flow
擷取網站上的圖片:
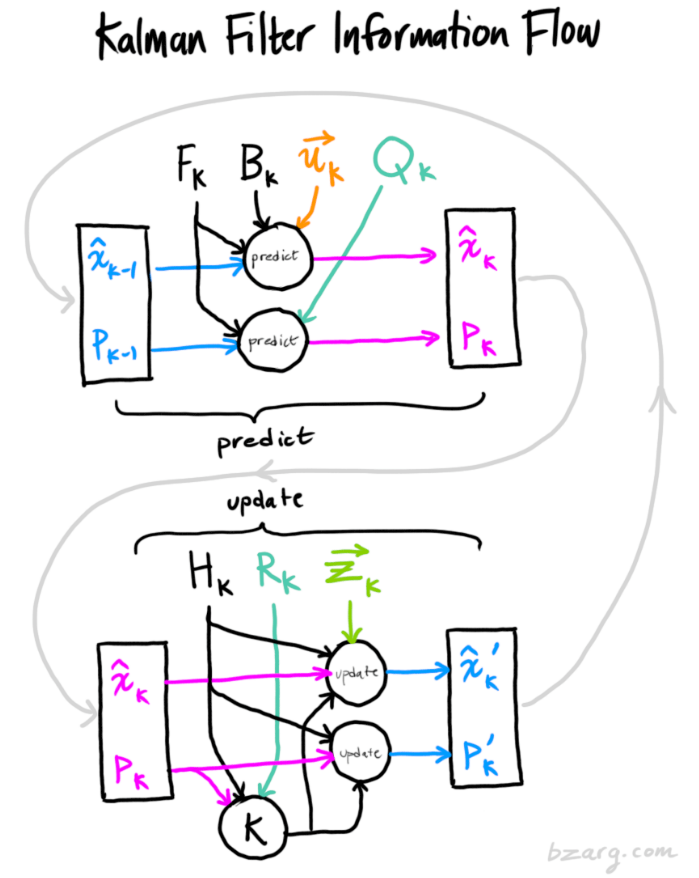
Lidar/Radar 的一些設定
state 定義為 \(x=(p_x,p_y,v_x,v_y)\) 分別是 (x 的位置, y 的位置, x 的速度, y 的速度)。
- \(F_k\) 會根據兩次 sensor data 之間的時間間隔 \(\vartriangle t\) 來表示:
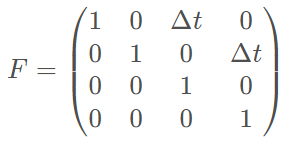
- 另外我們將 加速度考慮為一個 mean = 0, covariance matrix = Q 的一個 random noise 的話,式 (1) and (4) 必須做修改。

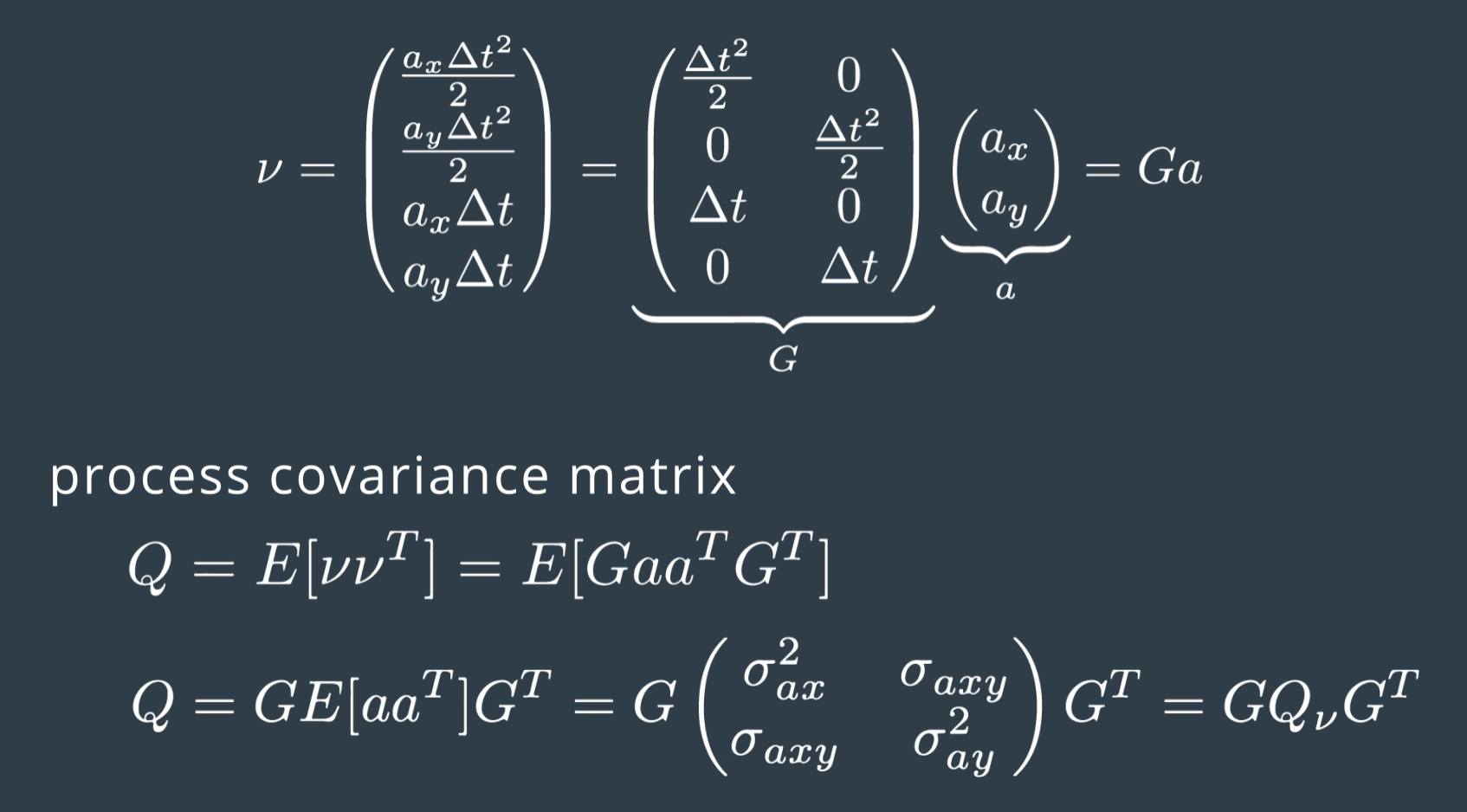
其中 \(Q_v\) 使用者自己設定調整,所以 state noise 的 covariance matrix 為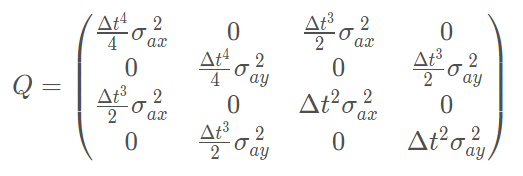
- Lidar 只會觀察到位置,因此 Lidar 的 \(H\) 為:$$H_{lidar}=
\left(
\begin{array}{clr}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0
\end{array}
\right)$$
Radar 就比較特別了,它觀察到的是以 polar coordinate 來表示。
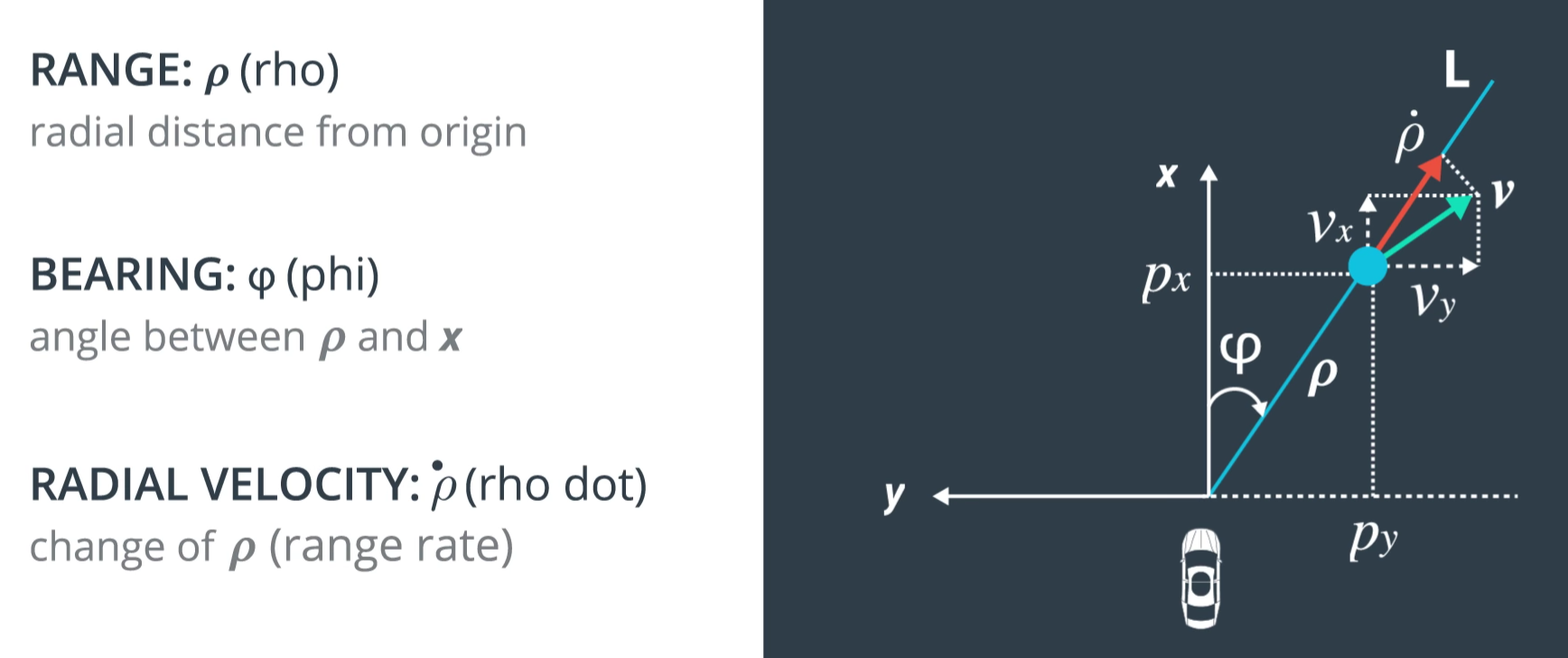
所以它的 states 和 observation 之間的關係無法用一個 matrix \(H\) 來代表,是如下的 non-linear 式子:$$\begin{align} h(x)= \left( \begin{array}{clr} \rho \\ \phi \\ \dot{\rho} \end{array} \right) = \left( \begin{array}{clr} \sqrt{p_x^2+p_y^2} \\ \arctan(p_y/p_x) \\ \frac{p_xv_x+p_yv_y}{\sqrt{p_x^2+p_y^2}} \end{array} \right) \end{align}$$ 為了讓它符合 state-space model 的線性式子,只好使用 Taylor 展開式,只使用 Jaccobian matrix 針對 \(h\) 去展開,而這個就是 Extended KF。
EKF
稍微改寫一下 Update Stage:
$$\begin{align}
y=(\vec{z}_k-H_k\hat{x}_k) \\
S=H_kP_kH_k^T+R_k \\
\hat{x}_k'=\hat{x}_k+Ky \\
P_k'=P_k-KH_kP_k \\
K=P_kH_k^TS^{-1}
\end{align}$$
在 EKF 中,由於我們使用 Taylor 展開式去逼近 \(h\),因此上述的 \(H_k\) 必須使用如下式子計算: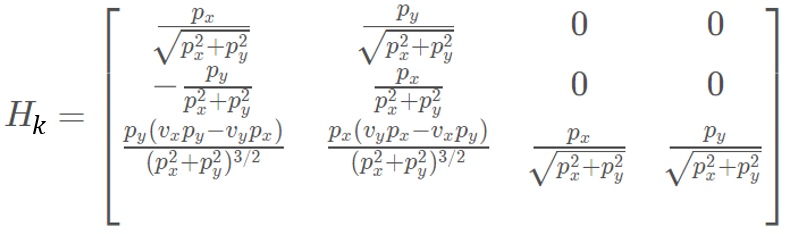
但是,這邊還有一個 tricky 的地方! 就是 式(18)直接使用式(17) \(h\) 的 non-linear function 計算!
回想一下我們將 \(h\) 做 linearlization 的目的: 就是式(5),(6)下的那張圖的轉換。如果 Gaussian pdf 經過 nonlinear 轉換後會變成 “非Gaussian”,因此只好做線性逼近。
既然線性轉換的 pdf 都已經是逼近了,不如就將 mean 使用最精確的值,因此 \(y\) 就直接使用式(17)計算。所以式(18)要改成:
$$\begin{align}
y=(\vec{z}_k-h(\hat{x}_k))
\end{align}$$
總結 Lidar and Radar Fusion
- [Predict]$$\hat{x}_{k}=F_k\hat{x}_{k-1} \\
P_k = F_kP_{k-1}F_k^T+Q$$
where
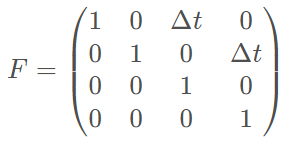
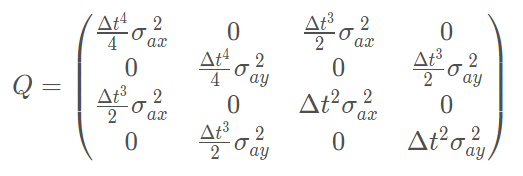
- [Lidar Update]$$y=(\vec{z}_k-H_{lidar}\hat{x}_k) \\ S=H_{lidar}P_kH_{lidar}^T+R_k \\ \hat{x}_k'=\hat{x}_k+Ky \\ P_k'=P_k-KH_{lidar}P_k \\ K=P_kH_{lidar}^TS^{-1}$$ where \(R_k\) sensor noise covariance matrix 由廠商提供, and $$H_{lidar}= \left( \begin{array}{clr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{array} \right)$$
- [Radar Update]$$y=(\vec{z}_k-h(\hat{x}_k)) \\
S=H_kP_kH_k^T+R_k \\
\hat{x}_k'=\hat{x}_k+Ky \\
P_k'=P_k-KH_kP_k \\
K=P_kH_k^TS^{-1}$$
where \(R_k\) sensor noise covariance matrix 由廠商提供, and $$h(x)=
\left(
\begin{array}{clr}
\rho \\
\phi \\
\dot{\rho}
\end{array}
\right)
=
\left(
\begin{array}{clr}
\sqrt{p_x^2+p_y^2} \\
\arctan(p_y/p_x) \\
\frac{p_xv_x+p_yv_y}{\sqrt{p_x^2+p_y^2}}
\end{array}
\right)$$
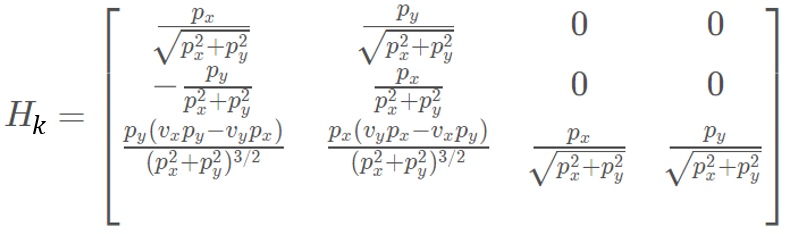
Reference
- How a Kalman filter works, in pictures
- Udacity Term2 Lecture