Framework of GAN

說來汗顏, 自從17年三月筆記完 WGAN 後, 就沒再碰 GAN 相關的東西了. 惡補了一下李宏毅GAN 的課程和其他相關資料, 因此筆記一下.

MMGAN(最原始的GAN), NSGAN(跟MMGAN差別在 G 的 update 目標函式有點不同), f-GAN, WGAN, ADDA (Adversarial Discriminative Domain Adaptation), infoGAN, VAE-GAN 等… 這些全部都是 follow 下面這樣的 framework:

$$\begin{align} Div\left(P_d\|P_G\right) = \max_D\left[ E_{x\sim P_d} D(x) - E_{x\sim P_G}f^*(D(x)) \right] \\ G^*=\arg\min_G{Div\left(P_d\|P_G\right)} + reg(G) \\ \end{align}$$

其中 $P_d$ 為 real data pdf, $P_G$ 為 generator 產生的 data pdf. $f^*$ 帶入不同的定義會產生不同的 divergence, 這之後會再說明.

式 (1) 定義了 $P_G$ 與 $P_d$ 的 divergence, 其中這個 divergence 的值為藉由解這個最佳化問題求得的.

式 (2) 表示要找的 $G$ 就是 divergence 最小的那個. Divergence 最小 ($=0$) 同時也表示 $P_G=P_d$ (生成器鍊成). 如果同時考慮 regularization term, $reg(G)$, 則會有很多變化產生, 如 ADDA, infoGAN, VAE-GAN…

我們接著來看 MMGAN, NSGAN, f-GAN, WGAN, ADDA, infoGAN, VAE-GAN 這些怎麼 fit 進這個框架.

MMGAN

MMGAN 是 MinMax GAN 的縮寫, 指的是最原始的 GAN.

將 (1) 中的 $D(x)$ 使用 $\log D(x)$ 替換, 並且 $f^*(t)=-\log(1-exp(t))$ 替換得到如下式子:

$$\begin{align} Div\left(P_d\|P_G\right) = \max_D\left[ E_{x\sim P_d} \log D(x) - E_{x\sim P_G}[-\log(1-D(x))] \right] \\ \end{align}$$

稍微再整理一下:

$$\begin{align} Div\left(P_d\|P_G\right) = \max_D\left[ E_{x\sim P_d} \log D(x) + E_{x\sim P_G}[\log(1-D(G(z)))] \right] \\ \end{align}$$

這就是 GAN discriminator 原始的式子.

而我們知道給定 $G$ 上述的最佳解為 $ D_G^*(x) = \frac{P_d(x)}{P_d(x)+P_G(x)} $, 並帶入 (4) 我們得到:

$$\begin{align} Div\left(P_d\|P_G\right) = -\log4+KL(p_d\vert\frac{p_d+p_g}{2})+KL(p_g\vert\frac{p_d+p_g}{2}) \\ =-\log4+2JSD(p_d \vert p_g) \end{align}$$

因此 discriminator 的最大化目的是計算出 JS divergence. 而 generator $G$ 求解沒什麼好說, 直接對 (3) 最小化:

$$\begin{align} G^*=\arg\min_G E_{x\sim P_G}[\log(1-D(x))] \end{align}$$

注意到與 (2) 對比, MMGAN 只是沒有 regularization term 而已.

NSGAN

NSGAN 為 Non-Saturating GAN 縮寫, 與 MMGAN 只差在 generator $G$ 求解式子不同, 原本是希望在一開始 generator 比較差的情形下用 (7) 算的 gradient 會太小, 因此改成下式, 使得 gradient 能在一開始的時候比較大, 讓 update 動起來.

NSGAN generator $G$ 為:

$$\begin{align} G^*=\arg\min_G E_{x\sim P_G}[-\log(D(x))] \end{align}$$

如果我們將 $ D_G^*(x) = \frac{P_d(x)}{P_d(x)+P_G(x)} $ 帶入並整理, 我們會發現:

$$\begin{align} G^*=\arg\min_G E_{x\sim P_G}[-\log(D^*(x))] \\ =\arg\min_G \left[ KL(P_G\|P_d)-2JSD(P_d\|P_G) \right] \end{align}$$

產生了兩個互相 trade-off 的 objective funtion… 這造成了矛盾

詳細推導請參考令人拍案叫绝的Wasserstein GAN 一文, 非常棒的文章. 引用文章內的說明:

一句话概括：最小化第二种生成器loss函数，会等价于最小化一个不合理的距离衡量，导致两个问题，一是梯度不稳定，二是collapse mode即多样性不足。

f-GAN

我們在 MMGAN 時提到 “將 (1) 中的 $D(x)$ 使用 $\log D(x)$ 替換, 並且 $f^*(t)=-\log(1-exp(t))$ 替換” 則會得到 discriminator 就是在求解 JS divergence. 那麼有沒有其他設定會產生其他 divergence 呢? 有的, 藉由 f-GAN 的定義可以囊括各式各樣的 divergence.

使用李老師的說明流程筆記: 首先定義 f-divergence, 可以發現 JSD, KL, reverse-KL, Chi square 等等都屬於其中的特例. 接著說明 convex function 的 conjugate function. 最後才說明怎麼跟 GAN 產生關聯 (神奇的連結).

f-divergence

$$\begin{align} Div_f(P\|Q)=\int_x q(x)f\left( \frac{p(x)}{q(x)} \right) dx \\ \text{where } f \text{ is }\color{orange}{convex} \text{ and } f(1)=0 \end{align}$$

明顯知道 $p(x)=q(x)$ 時 $Div_f(P|Q)=0$, 同時可以證明 $Div_f(P|Q)\geq 0$, 因此滿足 divergence 定義(search “Divergence (statistics) wiki” for definition):

$$\begin{align} Div_f(P\|Q)=\int_x q(x)f\left( \frac{p(x)}{q(x)} \right) dx \\ \geq f\left( \int_x q(x)\frac{p(x)}{q(x)} dx \right)=f(1)=0 \\ \end{align}$$

$f$ 是 convex 這點很重要, 才能將 (13) 到 (14) 使用 Jensen’s inequality. 定義不同 $f$ 會產生不同 divergence, 常見的為(李老師slide):

由於 $f$ 是 convex, 而每一個 convex function 都會有一個 conjugate function $f^*$ (它也是 convex), 利用這個特性最後可以跟 GAN 連起來. 因此以下先說明 conjugate function.

Fenchel Conjugate

Every convex function $f$ has a conjugate function $f^*$:

$$\begin{align} f^*(t)=\max_{x\in dom(f)}\{xt-f(x)\} \end{align}$$

老師的投影片非常形象的表示出 $f$ 與 $f^*$ 的關係L

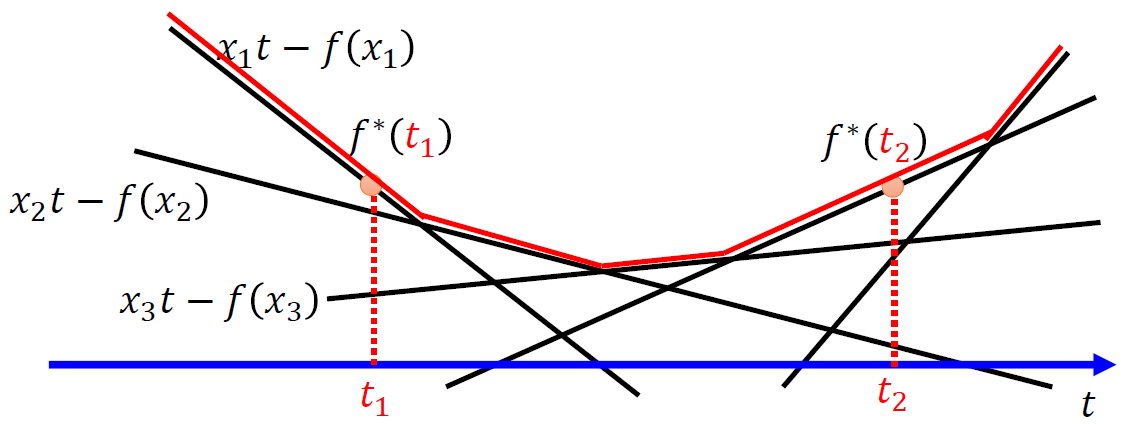
還具體舉了個當 $f(x)=x\log x$ 的例子:

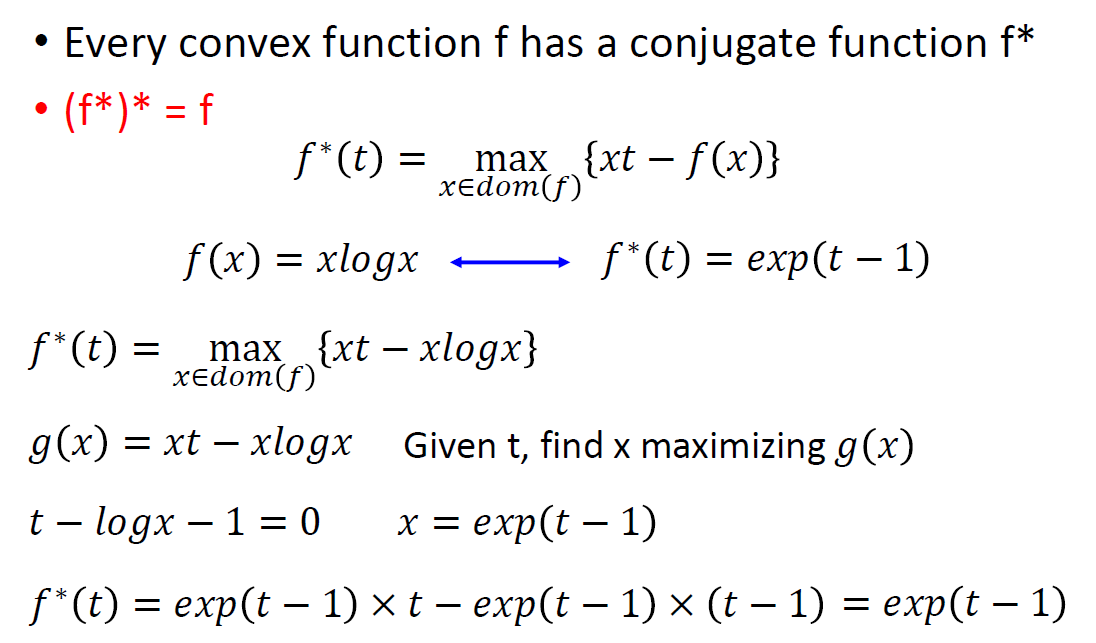
與 GAN 的關聯

這是我覺得非常厲害的地方. 首先 $f^*$ 的 conjugate 就變回 $f$ 了, 它們互為 conjugate.

$$\begin{align} f^*(t)=\max_{x\in dom(f)}\{xt-f(x)\}\longleftrightarrow f(x)=\max_{t\in dom(f^*)}\{xt-f^*(t)\} \end{align}$$

將 (11) 利用 conjugate 的關係重新表示一下

$$\begin{align} Div_f(P\|Q)=\int_x q(x)f\left( \frac{p(x)}{q(x)} \right) dx \\ =\int_x q(x) \left( \max_{t\in dom(f^*)} \left[ \frac{p(x)}{q(x)}t - f^*(t) \right] \right) dx \end{align}$$

厲害的地方來了…. 假設我們有一個 function $D$ 可以直接幫我們解出 (18) 的那個 $t$ 是什麼, 也就是:

$$\begin{align} D(x)=\hat{t}=\arg\max_{t\in dom(f^*)} \left[ \frac{p(x)}{q(x)}t - f^*(t) \right] \end{align}$$

那麼 $Div_f(P||Q)$ 直接就是

$$\begin{align} Div_f(P||Q)=\int_x q(x) \left[ \frac{p(x)}{q(x)}\hat{t} - f^*(\hat{t})) \right] dx \end{align}$$

實作上 $D$ 的表達能力有限, 同時讓我們找到最準的那個叫做 $\hat{D}$, 因此只能求得一個下界並整理一下得到:

$$\begin{align} Div_f(P||Q)\geq \int_x q(x) \left[ \frac{p(x)}{q(x)}\hat{D}(x) - f^*(\hat{D}(x))) \right] dx \\ \approx \int_x q(x) \left[ \frac{p(x)}{q(x)}\hat{D}(x) - f^*(\hat{D}(x))) \right] dx \\ = \int_x {p(x)\hat{D}(x)}dx - \int_x{q(x)f^*(\hat{D}(x))} dx \\ = E_{x\sim P}\left[ \hat{D}(x) \right] - E_{x\sim Q}\left[ f^*( \hat{D}(x) ) \right] \\ = \max_D \left[ E_{x\sim P}\left[ D(x) \right] - E_{x\sim Q}\left[ f^*( D(x) ) \right] \right] \\ \end{align}$$

請把 (25) 跟 (1) 比較, 其實就一模一樣.

因此, 只要 $f$ 是 convex function , 且 $f(1)=0$, discriminator $D$ 的最佳化問題 ((1) 用 $f$ 的 conjugate, $f^*$, 帶入) 就是在計算兩個分布的 f-divergence.

論文直接給出各種 f-divergence 的 $f$ and $f^*$

因此我們可以發現 MMGAN 和 LSGAN 都是 f-GAN 的一種特例.

WGAN

具體請參考之前自己筆記的文章

李老師的講義對於 Earth Mover’s Distance (或稱 Wasserstein distance) 講解得很清楚, 其中的一個參考連結更解釋了 Wasserstein distance 如何轉換成求解 $\max_D$ 且 $D$ 必須限制在 Lipschitz 條件下.

總之這裡要說的是, Wasserstein distance 不屬於 f-divergence, 但也完全 follow 我們一開始說的 (1) & (2) 的架構:

令 $f^*(x)=x$ 同時多一個限制是 $D\in k-Lipschitz$

$$\begin{align} Div\left(P_d\|P_G\right) = \max_{D\in k-Lipschitz}\left[ E_{x\sim P_d} D(x) - E_{x\sim P_G}D(x) \right] \\ \end{align}$$

求解 discriminator 的最佳化問題其實就是在估算兩個分布的 divergence.

原始論文針對 $D\in k-Lipschitz$ 的限制直接用很暴力的 weight clipping 方法解掉. 因此後面有一篇 WGAN-GP (Gradient Panelty) 的方式補強. 這裡不展開討論, 因為我也沒什麼研究, 簡單帶過一點待讀的論文. 另外有一篇 SN-GAN “Spectral Normalization for Generative Adversarial Networks“ 看起來是一種主流訓練 WGAN 的方式, 事先就將 gradient 都限制 norm<=1. 這篇文章大致整理各種變體, 參考連結.

關於 regularization term, $reg(G)$

Adversarial Domain Adaptation

我們先說 Domain-Adversarial Training of Neural Networks 這篇經典的文章. Generator 現在做的是 feature extractor 的工作, 而我們希望 target domain 的 feature 能跟 source domain 的 feature 分佈一樣, 這樣在 source domain (有 label) 訓練好的 model, 就能直接在 target domain (無 label) 上作用.

要做到無法區分出這個 feature 是 source or target domain 這件事情….正好就可以用 GAN 的方式達到.

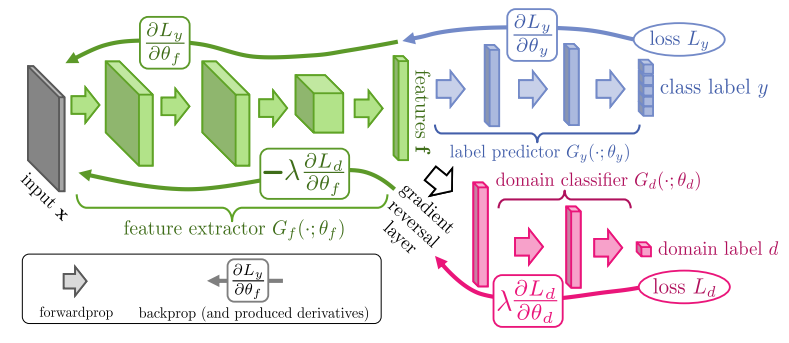
不看 Label Predictor 的部分的話, 就是一個典型的 GAN. 作用就是把 source and target 的 feature 投影到共同的空間, 並且分不開. 但缺少 Label Predictor 有可能造成 feature extractor 產生 trivial solution (例如全部 map 到 constant) 這樣也能使 discriminator 分不開.

因此加上 Label Predictor 除了避免這件事外, 也保證在 source domain 能夠很好的完成我們的分類任務. 注意, 因為 label 只有在 source domain, 因此 label predictor 只能保證 source domain 的分類. 但由於我們把 feature 用 GAN 消除了 domain 之間的差異, 因此我們才能期望這時候的 source domain classifier 也能作用在 target domain.

論文使用了一個叫做 Gradient Reversal Layer (GRL), 其實我們可以忽略這件事情, 因為這只是 discriminator and generator 一個 maximize 另一個 minimize, 而使得要 update generator 時當時算的 discriminator gradient 要取負號. 我們照正常的 GAN training 就可以了.

Label Predictor 的 loss 具體就是 (2) 的 regularization term, $reg(G)$. 這是希望我們 train $G$ 的時候除了要欺騙 $D$, 同時要能降低 $reg(G)$ (prediction loss).

後續有一篇 Advesarial Discriminative Domain Adaptation 算是豐富了這種架構. 論文裡對 source and target 的 feature extractor 使用不同的 neural networks. 並且一開始的 source domain feature extractor 是事先訓練好的. 然後後面的 GAN 部分訓練的時候, target domain 的 feature extractor 要去匹配 source domain 的. 這樣做的好處是至少一邊的分佈是固定住的, 比較容易訓練. 同時也簡化了訓練流程, 見下圖:

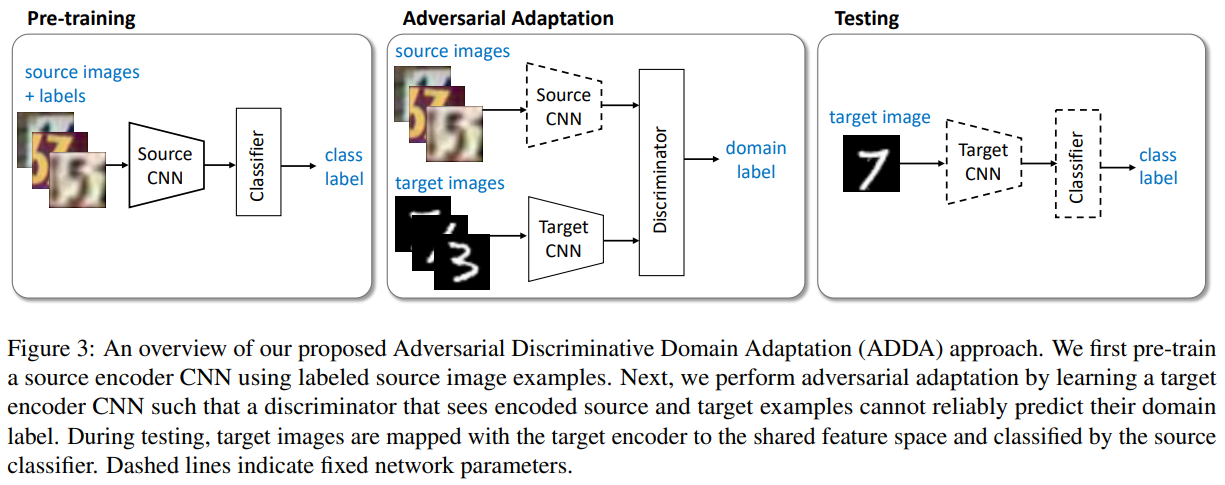
infoGAN

詳細就不解釋了, 事實上推導較複雜但實作上卻異常容易, 之後有機會再記錄一下. 總之在原始 GAN 架構上多了一個 Decoder, 用來還原 generator input 中所指定的部分($c$). Decoder 希望能將 $c$ 無損的還原, 那麼什麼叫無損? 指的就是 Mutual Information of $c$ and $\hat{c}$ 最大. 其中 $\hat{c}$ 表示由 Decoder 還原出來的結果.

還原的 loss term 基本就是 $reg(G)$, 同樣的理解, $G$ 除了要騙過 $D$ 之外, 多了一個任務就是使得還原的 loss 愈小愈好.

附上李宏毅教授課程的兩張圖片:

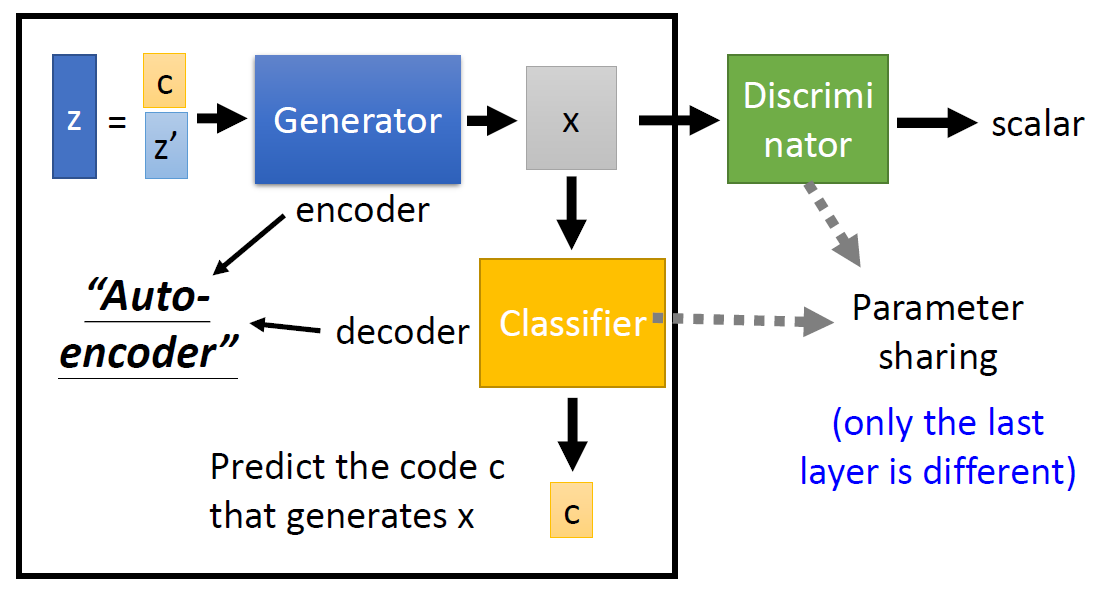
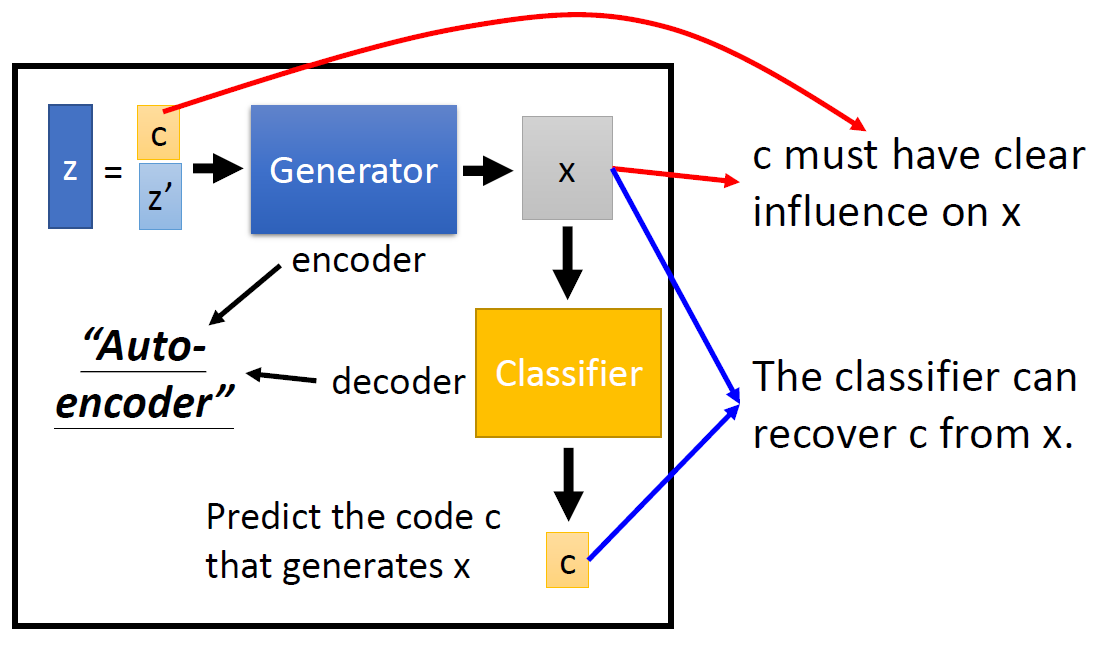
VAE-GAN

直接上老師的 slides

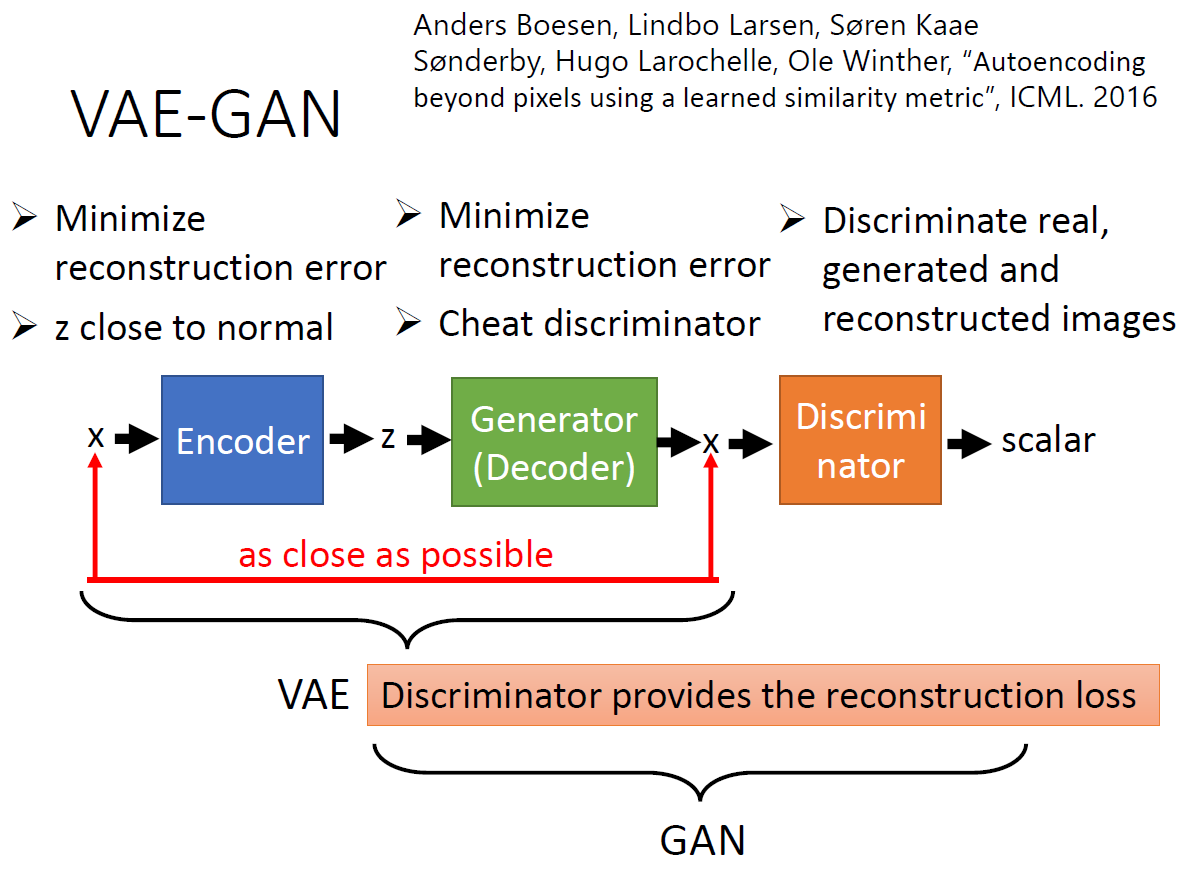
以 GAN 的角度來看, $G$ 除了要欺騙 $D$ 之外, 還多了 VAE 的 loss ($reg(G)$) 用來 reconstruct 原本的 input image. 對 GAN 來說是有好處的, 因為 GAN 雖然能夠產生夠真的 image, 但是會自己”捏造”, 因此多了 VAE 的 $reg(G)$ 會讓捏造的情況降低.
以 VAE 的角度來看, GAN 的 loss 變成了 regularization term 了. 也就是說 VAE 除了要產生跟原本接近的 image (pixel-level), 還要能騙過 $D$. 這是為了補足 VAE 的缺點, 原始 VAE 的目標函式是 pixel-level 的 l2-norm, 這跟人類認為的真實不真實不一致, 因此 AVE 會產生模糊的 image. 用 GAN 的 loss 當成 regularization term 則補足了 VAE 這點.

因此 VAE-GAN 這是個互惠的結構, 很漂亮. 這個結構新的一篇 Adversarial Latent Autoencoders 粗略講也是 VAE-GAN 架構, 只是 reconstruction 不是再 image, 而是在 latent space. 論文結果十分驚艷, github.

結論

本篇開頭說明的 framework 基本可以解釋了上述各種 GAN. 但由於本魯才疏學淺, 還有一大堆沒看的變種, EBGAN, BEGAN, CycleGAN, …etc. 只能說之後讀到的時候, 看看能否試著這麼解釋. GAN 實在太多了, 可以看看 GAN Zoo 有多少用 GAN 來命名的架構(似乎停止更新).