Gumbel-Max Trick

我們在介紹 VAE 的時候有說明到 re-parameterization trick, 大意是這樣的

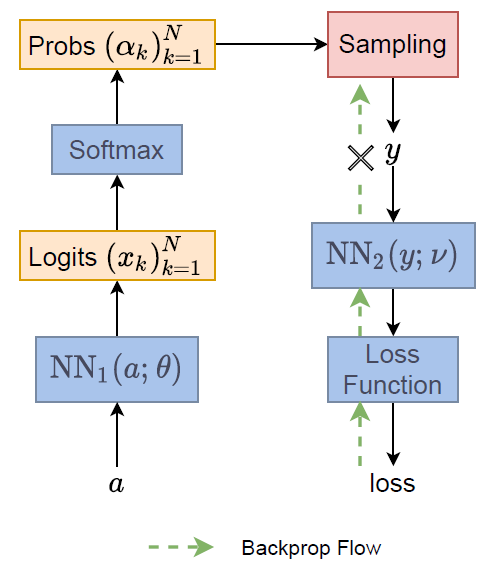
$y$ 是 sampling from distribution $\alpha$, i.e., $y=\text{Sampling}(\alpha)$, 其中 $\alpha=\text{NN}_1(a;\theta)$
由於我們有採樣, 因此 loss 採用期望值. Loss function 為:

$$\begin{align} L = \mathbb{E}_{y\sim\alpha}[\text{NN}_2(y;\nu)] \end{align}$$

Loss 對 $\theta$ 偏微分的時候會失敗, 主要是因為:

$$\begin{align} \nabla_\theta L = \nabla_\theta \mathbb{E}_{y\sim\alpha}[\text{NN}_2(y;\nu)] \\ \neq \mathbb{E}_{y\sim\alpha}[\nabla_\theta \text{NN}_2(y;\nu)] \end{align}$$

微分不能跟 Expectation 互換是因為 sampling 的 distribution $\alpha$ 其實也是 depends on $\theta$.

因此在 VAE 那邊的假設就是將 $\alpha$ 定義為 Gaussian pdf. 因此可以變成:

$$\begin{align} \nabla_\theta L = \nabla_\theta \mathbb{E}_{y\sim\alpha}\left[ \text{NN}_2(y;\nu) \right] \\ = \nabla_\theta \mathbb{E}_{\varepsilon\sim N(0,I)}\left[ \text{NN}_2(\mu+\sigma\varepsilon; \nu) \right] \\ = \mathbb{E}_{\varepsilon\sim N(0,I)}\left[ \nabla_\theta \text{NN}_2(\mu+\sigma\varepsilon; \nu) \right] \end{align}$$

採樣變成從一個 跟 $\theta$ 無關的分布, 因此微分跟期望值就能互換, 所以可以做 backprop.

現在的情況是如果是 Gaussian 的情形很好做變換, 但如果是 categorical distribution 該怎麼辦呢?

什麼情況會遇到 categorical distribution? 在 reinforcement learning 時, $\text{NN}_1$ predict 出例如 4 個 actions 的機率, 我們需要隨機採樣一種 action, 然後傳給後面的 NN 去計算 reward.
(其實我不熟 RL, 看網路上的文章說的)

Gumbel max trick 就提供了解法!

Gumbel Distribution and Gumbel Max Sampling

這一篇文章 The Humble Gumbel Distribution 提供了非常清晰的解釋, 十分推薦閱讀

假設我們經由一個 network 算出 logits $(x_k)_k$, 一般我們如果要 sampling 的話還必須過 softmax 讓它變成機率 $(\alpha_k)_k$, 然後在用例如 np.random.choice 根據機率採樣出結果.

現在 sampling 流程改為:

先從標準 Gumbel 分佈 (先不管這分佈長什麼樣) 採樣出 $N$ 個值, 令為 $(G_k)_k$, 讓它跟 logits 相加: $z_k=x_k+G_k$, 然後 $\text{argmax}_k (z_k)$ 就是我們這次的採樣結果

圖示為:

注意到我們唯一的一個採樣動作完全跟 network 的參數 $\theta$ 無關! 因此 re-parameterization trick 就能用上. (先假設 $\text{argmax}_k (z_k)$ 可微, 因此可以 backprop, 這等下會說)
剩下唯一不確定的就是, 這樣的採樣行為出來的結果, 會跟使用 $(\alpha_k)_k$ 的機率分佈採樣出來一樣嗎 ?
換句話說, $\text{argmax}_k (z_k)$ 出來的結果, 其結果的分佈是不是符合 $(\alpha_k)_k$ ?
程式驗證可參考 The Humble Gumbel Distribution, 將最主要的部分修短擷取後如下:

# Modified from http://amid.fish/humble-gumbel
import numpy as np
import matplotlib.pyplot as plt
# Assign categorical probabilities, for example:
probs = [0.13114754, 0.01639344, 0.21311475, 0.24590164, 0.19672131, 0.06557377, 0.13114754]
n_classes = len(probs)
logits = np.log(probs)  # logits is log probability (with constant offset)
n_samples = 10000  # experimental number of sampling
def gumbel_sampling(logits):
    noise = np.random.gumbel(size=len(logits))
    sample = np.argmax(logits + noise)
    return sample
samples_with_gumbel_max_trick = [gumbel_sampling(logits) for _ in range(n_samples)]
samples_from_true_distribution = np.random.choice(np.arange(n_classes), size=n_samples , p=probs)
# Plotting area, comparing `samples_with_gumbel_max_trick` and `samples_from_true_distribution`
def plot_estimated_probs(samples, n_classes):
    estd_probs, _, _ = plt.hist(samples,
                                bins=np.arange(n_classes + 1),
                                align='left',
                                edgecolor='white',
                                density=True)
    plt.xlabel("Category")
    plt.ylabel("Estimated probability")
    return estd_probs
plt.figure()
plt.subplot(1, 2, 1)
plot_estimated_probs(samples_from_true_distribution, n_classes)
plt.title('Sampling from true pdf')
plt.subplot(1, 2, 2)
estd_probs = plot_estimated_probs(samples_with_gumbel_max_trick, n_classes)
plt.title('Sampling with Gumbel-max trick')
plt.tight_layout()
plt.show()

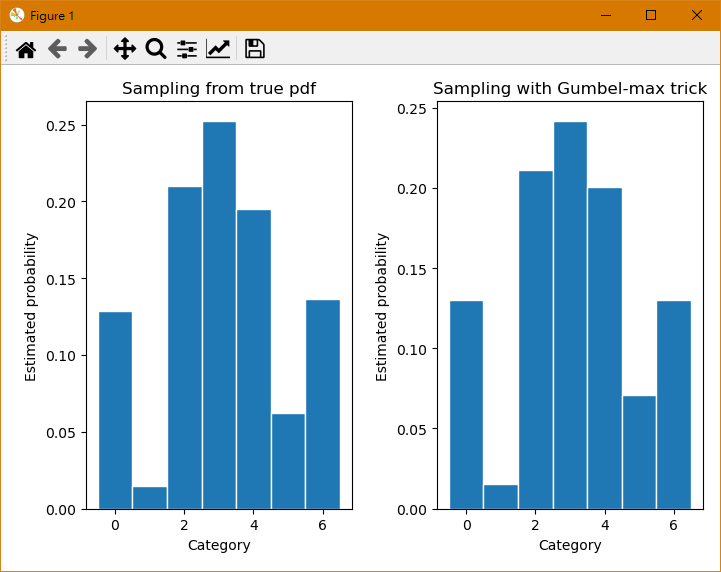
可以看到用 Gumbel-max trick 採樣出來的 samples 其分佈跟真實的機率分佈十分接近.
事實上可以證明會是一樣的, 在下一節我們將證明寫出來.
再囉嗦一下, 不要忘記了, 使用 np.random.choice 對真實分佈採樣是沒有辦法做 backprop 的 (見 eq (2) (3))
而透過 Gumbel-max trick 我們可以從一個與要 optimize 的參數 $\theta$ 無關的分佈 (Gumbel distribution) 進行採樣, 才能利用 re-parameterization trick 做 backprop (例如 eq (4)~(6) 的概念)

其實我少講了一件事, np.argmax 不可微, 所以不能 backprop. 因此一個實際的做法是使用 softmax (with temperature) 近似:

$$\begin{align} \text{softmax}(z_k,\tau)=\frac{\exp(z_k/\tau)}{\sum_{i=1}^N\exp(z_i/\tau)} \end{align}$$

實作上會先讓 temperature $\tau$ 從比較大的值開始 (比較不那麼凸顯值之間大小的差異), 之後慢慢變小接近 $0$ (等同於 argmax). 參考 paper 的圖:

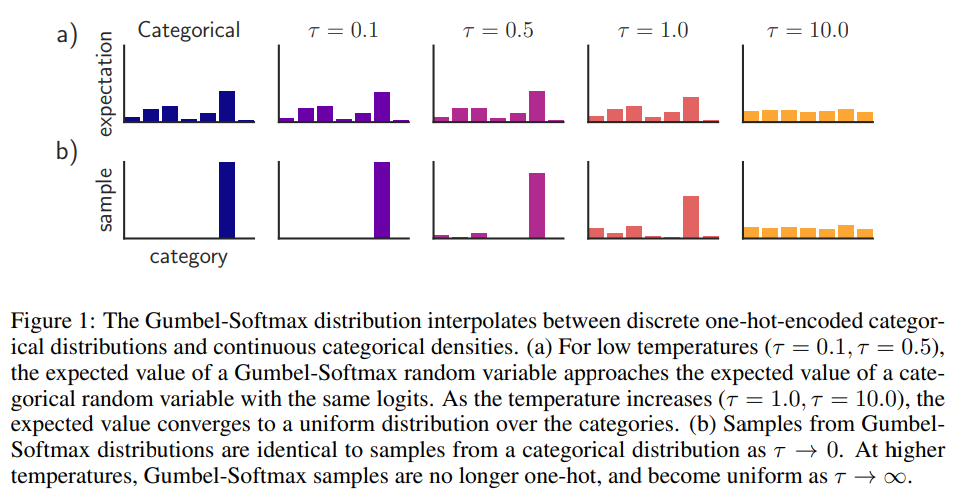
Proof of Gumbel-Max Trick for Discrete Distributions

其實完全參考 The Gumbel-Max Trick for Discrete Distributions, 但最後一行的推導用看的實在沒看出來, 因此自己補齊完整一點

Math warning, 很枯燥

Gumbel PDF:
- $f(z;\mu)=\exp\left[-(z-\mu)-\exp\left[-(z-\mu)\right]\right]$
- $f(z;0)=\exp\left[-z-\exp\left[-z\right]\right]$
Gumbel CDF:
- $F(z;\mu)=\exp\left[-\exp\left[-(z-\mu)\right]\right]$
- $F(z;0)=\exp\left[-\exp\left[-z\right]\right]$

Categorical distribution 例如分成 $N$ 類, NN 通常最後會輸出一個 logits vector, $(x_k)_k$, $k=1…N$

$z_k=x_k+G_k$, 其中 $G_k$ 是一個標準 Gumbel distribution (mean=0, scale=1)

$$\begin{align} \Pr(k\text{ is largest}|\{x_i\},z_k) = \Pr(\max_{i\neq k}z_i<z_k) \\ =\prod_{i\neq k}\Pr(z_i<z_k) = \prod_{i\neq k}\Pr(x_i+G_i<z_k) \\ =\prod_{i\neq k}\Pr(G_i<z_k-x_i) \\ =\prod_{i\neq k}F(z_k-x_i;0) \\ =\prod_{i\neq k}\exp\{-\exp\{-z_k+x_i\}\} \end{align}$$ $$\begin{align} \therefore \Pr(k\text{ is largest}|\{x_i\})=\int\Pr(z_k)\Pr(k\text{ is largest}|\{x_i\},z_k)dz_k \\ = \int f(z_k-x_k;0)\prod_{i\neq k}\exp\{-\exp\{-z_k+x_i\}\} \\ = \int \left(\exp\{-z_k+x_k-e^{-z_k+x_k}\}\right) \prod_{i\neq k}\exp\{-e^{-z_k+x_i}\} dz_k \\ =\int \exp\{-z_k+x_k\}\prod_{i=1}^N{ \exp\{-e^{-z_k+x_i}\} } dz_k \\ = \int \exp\{-z_k+x_k\} \cdot \exp\{-\sum_{i=1}^Ne^{-z_k+x_i}\} dz_k \\ =\int \exp\{-z_k+x_k-\sum_{i=1}^Ne^{-z_k+x_i} \} dz_k \\ =\int \exp\{-z_k+x_k-e^{-z_k} {\color{orange}{\sum_{i=1}^Ne^{x_i}}} \} dz_k \\ =\int \exp\{-z_k+x_k- {\color{orange}A} e^{-z_k} \} dz_k \end{align}$$

這裡我們為了方便定義 $A=\sum_{i=1}^N e^{x_i}$

$$\begin{align} =\int \exp\{-z_k+x_k - {\color{orange}{e^{\ln A}}} e^{-z_k} \} dz_k \\ = e^{x_k} \int \exp\{-z_k-e^{-z_k + \ln A}\} dz_k \\ = e^{x_k} \int \exp\{-z_k {\color{orange}{+\ln A-\ln A}} -e^{-z_k + \ln A}\} dz_k \\ = e^{x_k}\cdot e^{-\ln A} \int \exp\{-(z_k-\ln A)-e^{-(z_k-\ln A)}\} dz_k \\ = \frac{e^{x_k}}{A} \int f(z_k;\ln A) dz_k \\ = \frac{e^{x_k}}{\sum_{i=1}^N e^{x_i}} \end{align}$$

Gumbel Distribution and Gumbel Max Sampling

Proof of Gumbel-Max Trick for Discrete Distributions

Reference