PRML book sampling (chapter 11) 開頭把動機描述得很好, 也引用來當這篇文章的前言.
在用 machine learning 很多時候會遇到需要計算某個 function $f(x)$ 的期望值, 當 $x$ follow 某個 distribution $p(x)$ 的情況, i.e. 需計算
例如 EM algorithm 會需要計算 $\mathbb{E}_{p(z|x)}[f(x,z)]$, 參考 ref 的式 (23), (28)
又或者我們要做 Bayesian 的 prediction 時, 參考 ref 的式 (2)
這些情況大部分都無法有 analytical form. 不過如果我們能從給定的 distribution $p(x)$ 取 $L$ 個 sample 的話, 式 (1) 就能如下逼近
$$\begin{align} \mathbb{E}_p[f] \approx \hat f:= \frac{1}{L}\sum_{l=1}^L f(x_l) \end{align}$$我們先來看一下 $\hat f$ 這個估計的期望值是什麼:
$$\begin{align} \mathbb{E}_p[\hat f]=\mathbb{E}_p\left[ \frac{1}{L}\sum_{l=1}^L f(x_l) \right] = \frac{1}{L}\sum_{l=1}^L\mathbb{E}_p\left[ f(x_l) \right] = {E}_p [f] = \mu \end{align}$$得到一個好消息是我們只要估超多次的話, $\hat f_1, \hat f_2, …$ 這些估計的平均就是我們要的值
其實這等同於估一次就好, 但用超大的 $L$ 去估計. 問題是 $L$ 要多大才夠 ? 如果變數 $x$ 的維度增加, 需要的 $L$ 是否也要增加才會準確 ? i.e. 會不會有維度爆炸的問題 ? (參考 Curse of dimensionality [1])
我們可以證明 (see Appendix):
$$\begin{align} var[\hat f]=\frac{1}{L}var(f) \end{align}$$這告訴我們, 隨著 sample 數量 $L$ 愈大, 我們估出來的 $\hat f$ 的”變化”會愈來愈小 (成反比). 更重要的是, 這跟 input dimension 無關! 所以不會有維度爆炸的問題.
課本說通常 $L$ 取個 10 個 20 個估出來的 $\hat f$ 就很準了. (其實很好驗證)
所以剩下要解決的問題便是, 要怎麼從一個給定的 distribution 取 sample ?
本篇正文從這開始
- 先說明 1-d 情況下的 r.v. 怎麼 sampling
- 再來說明如何用 Markov chain sampling, 也就是大名鼎鼎的 MCMC (Markov Chain Monte Carlo)
- 最後介紹兩個實作方法 Gibbs and Metropolis-Hasting sampling.
以下文章內容絕大多數都是從 Coursera: Bayesian Methods for Machine Learning 課程來的
非常推薦這門課程!
從 1-D 說起
Discrete case
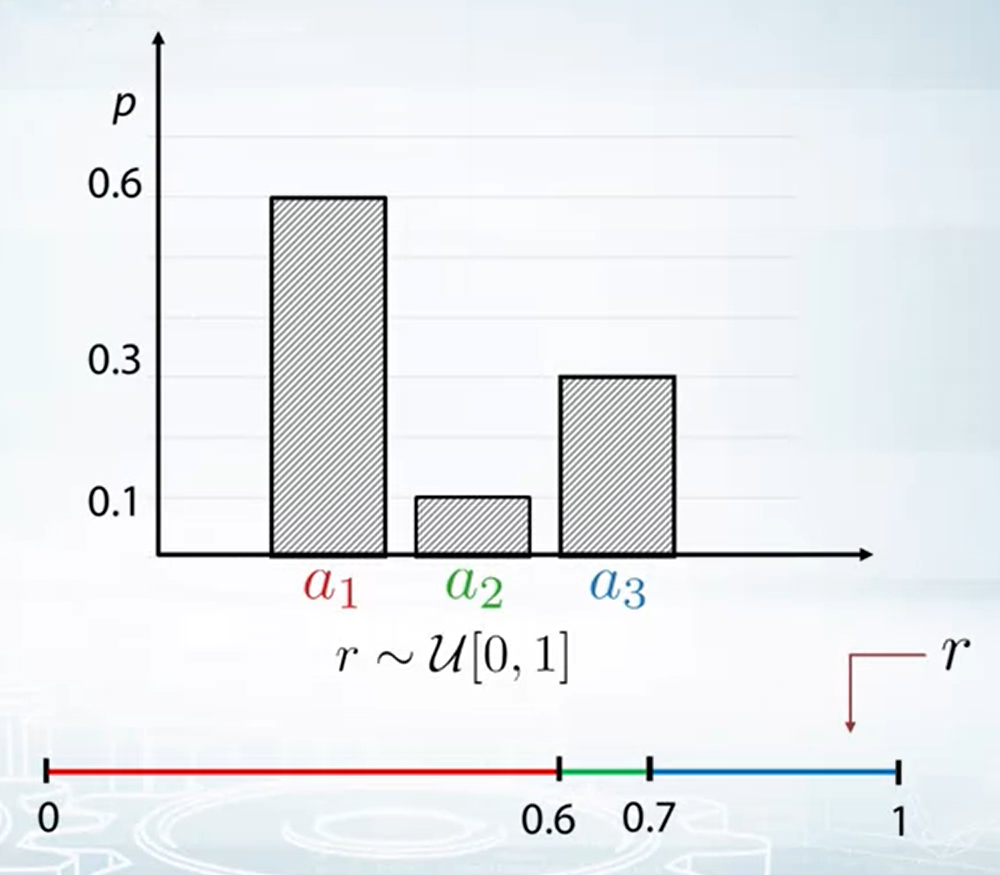
先討論 discrete distribution 的情形, 我們總是可以取 samples from uniform distribution [0, 1], i.e. $\text{sample} \sim \mathcal{U}[0,1]$
所以若要從下圖例子的 discrete distribution 取 samples 其實很容易, 若落在 [0, 0.6) 就 sample $a_1$, 落在 [0.6, 0.7) 取 $a_2$, 落在 [0.7, 1) 取 $a_3$.
Gaussian case
如果是 continuous distribution 呢?
考慮如下的 standard Gaussian distribution $\mathcal{N}(0,1)$
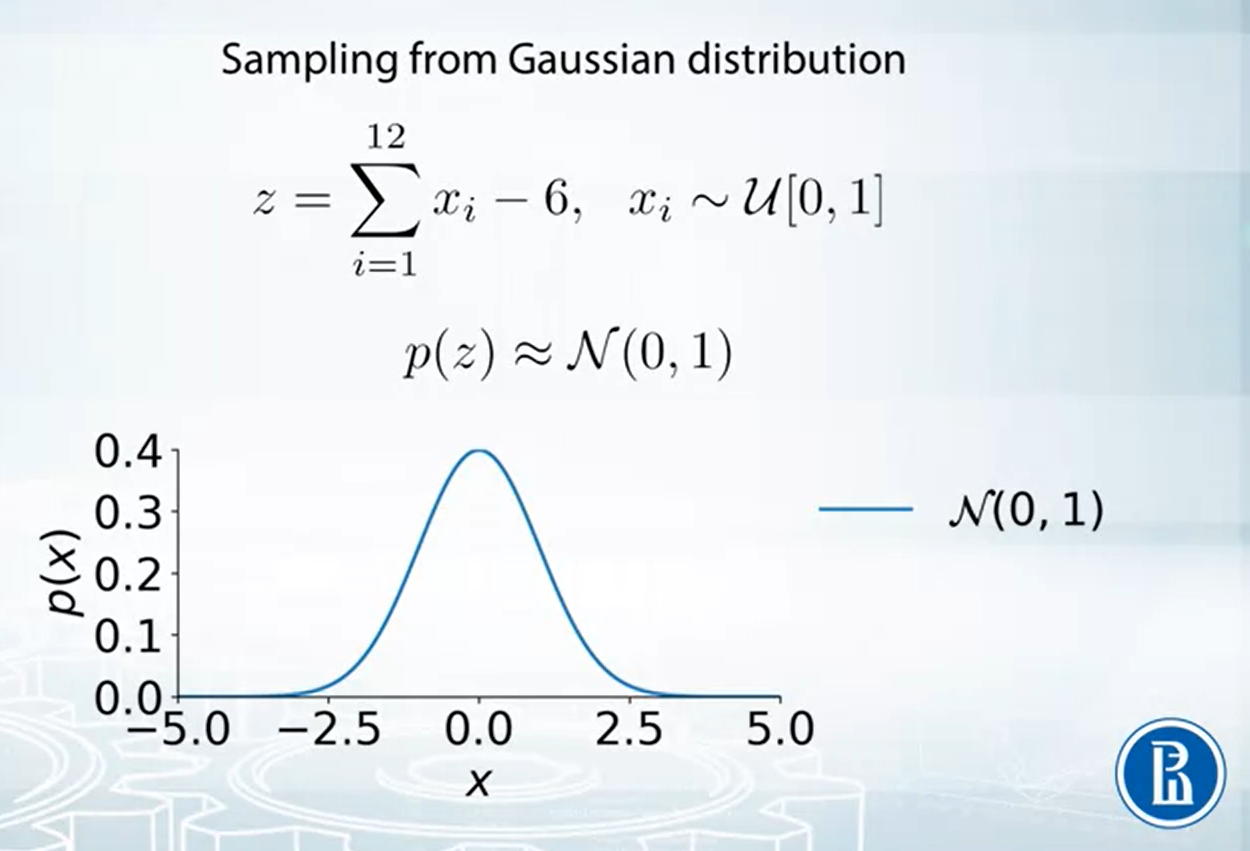
可以使用 Central Limit Theorem. 舉例來說我們可以從 $n$ 個 I.I.D. 的 $\mathcal{U}[0,1]$ 取 samples, 然後平均起來. CLT 告訴我們當 $n$ 很大的時候, 結果分布會接近 $\mathcal{N}(0,1)$
General continuous case
那如果是 general case 呢?
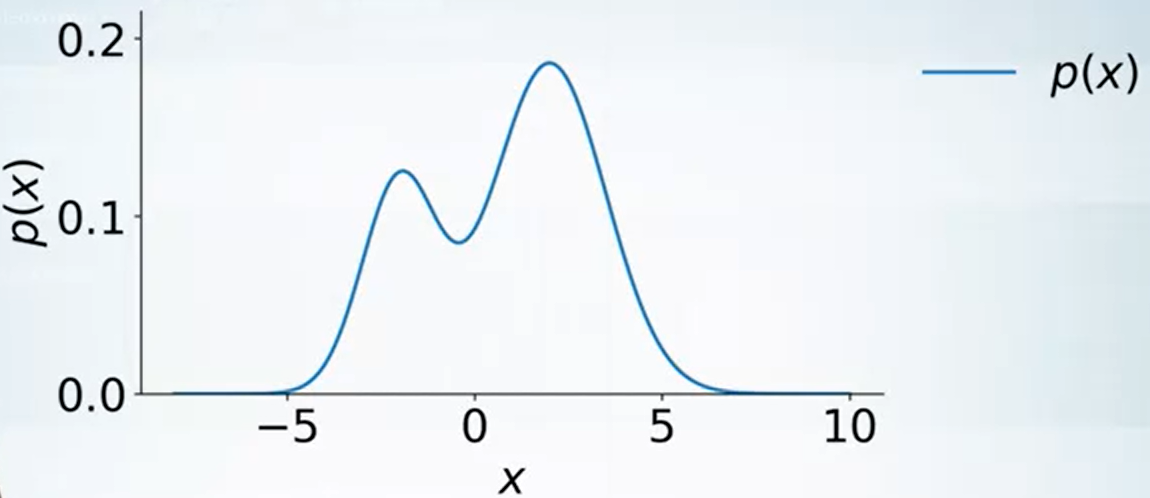
方法是找一個已知會 sampling 的分布乘上 constant value 使它成為 upper bound
例如利用 $2q(x)=2\mathcal{N}(1,9)$ 可以變成 $p(x)$ 的 upper bound
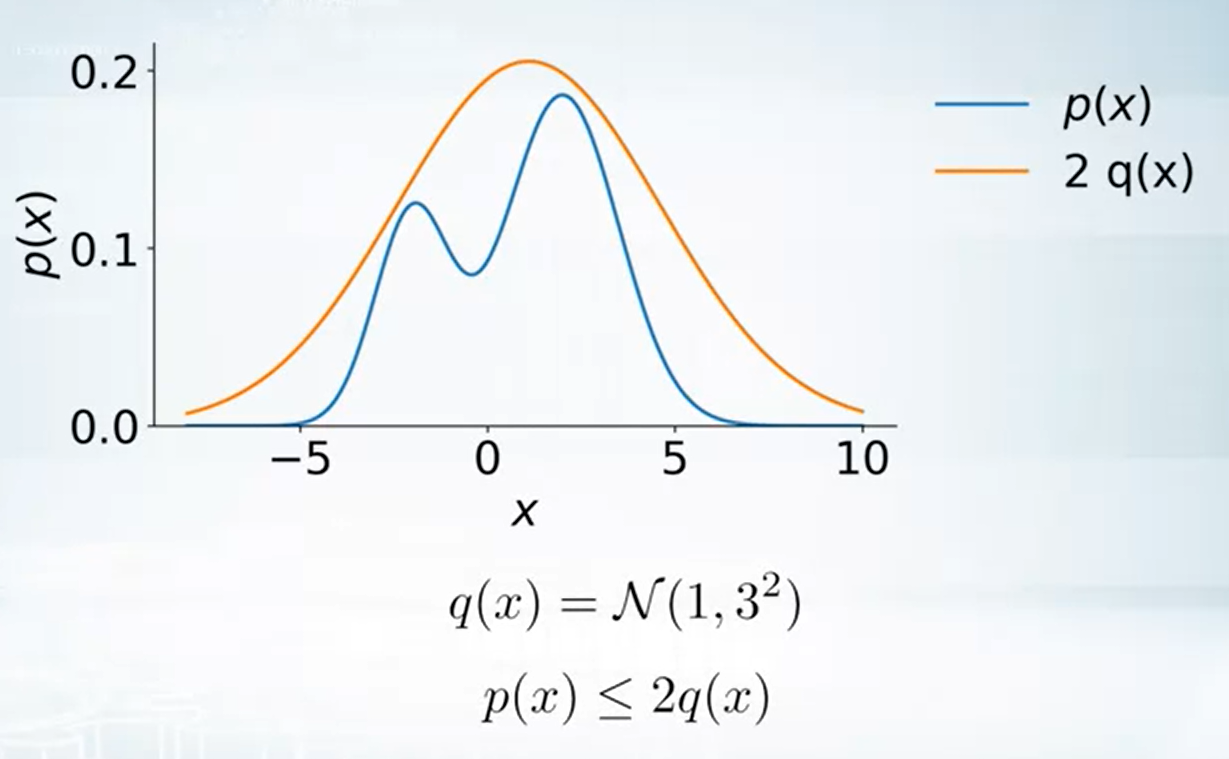
因此我們可以 sample $\tilde{x}$ from $2q(x)$, 舉例來說很有可能 $\tilde{x}=0$ 因為在 $0$ 附近的機率最大. 但是對於我們真實想要 samping 的 $p(x)$ 來說, $0$ 反而機率比較小. 因此我們要有一些 rejection 機制.
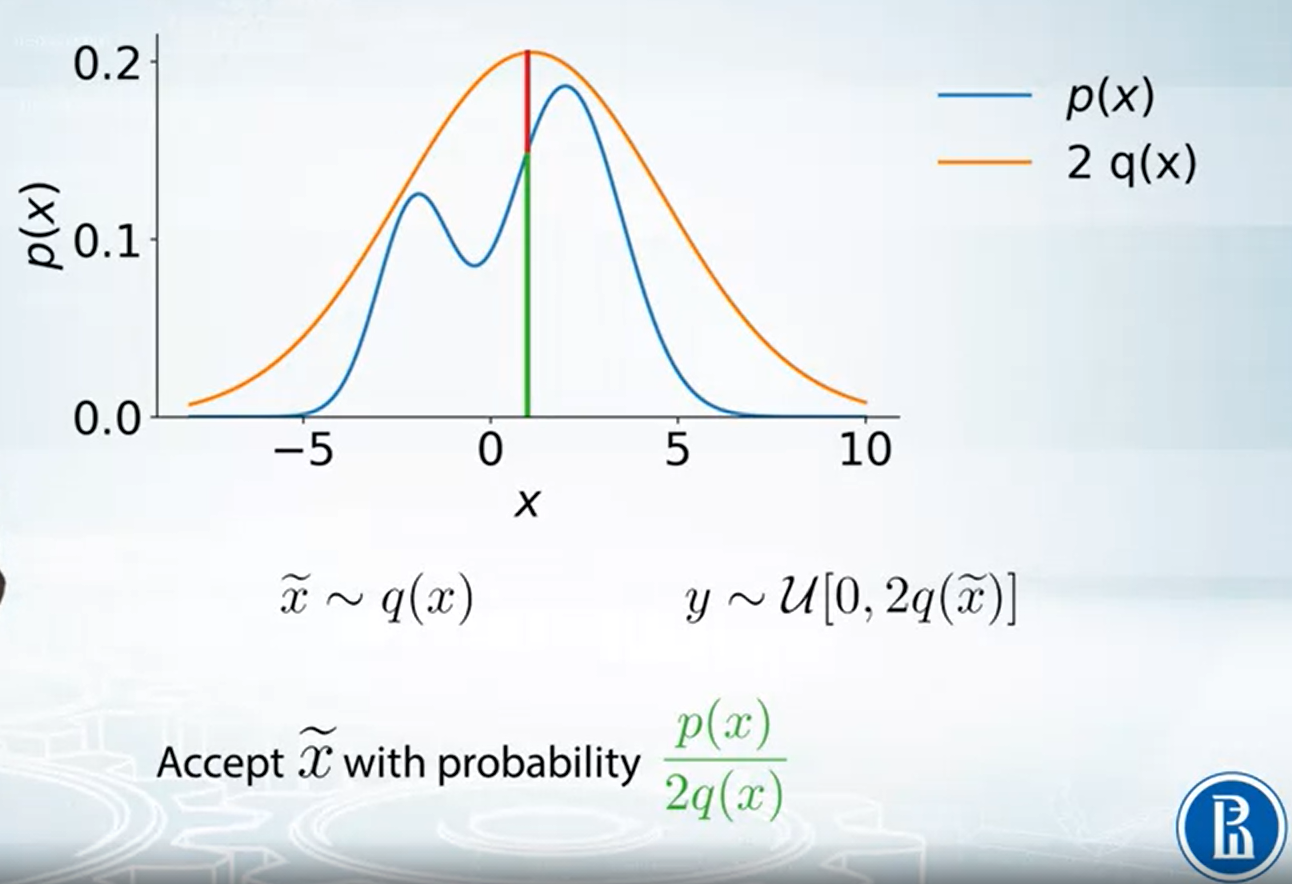
所以流程就是, 首先先從已知的 $q(x)$ sample 出 $\tilde{x}$, 由於 $2q(x)$ 是 $p(x)$ 的 upper bound, 因此我們可以根據比例來決定這一次的 $\tilde{x}$ 是否接受. 上圖紅色為 rejection 而綠色為 acception. 因此 acception 機率為:
$$\begin{align} \frac{p(x)}{2q(x)} \end{align}$$我們解釋一下為何這方法可以運作, 首先注意到所有取出來的 $\tilde{x}$ (還沒拒絕之前) 是均勻分布在 $2q(x)$ curve 下的 (見下圖). 而一旦引入我們 rejection 的方法, 取出來的點就是均勻分布在我們要的 $p(x)$ curve 下了.
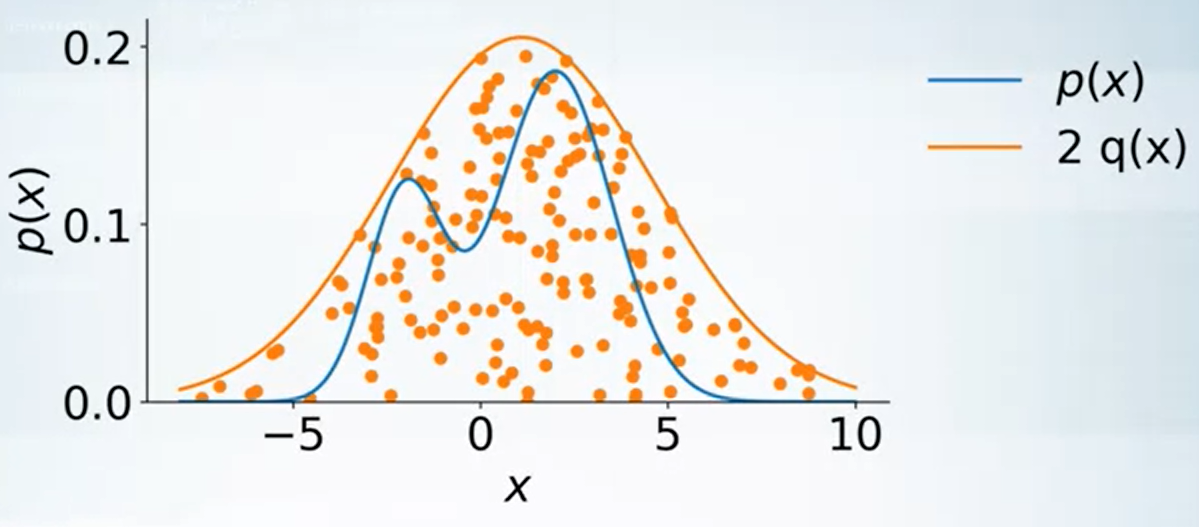
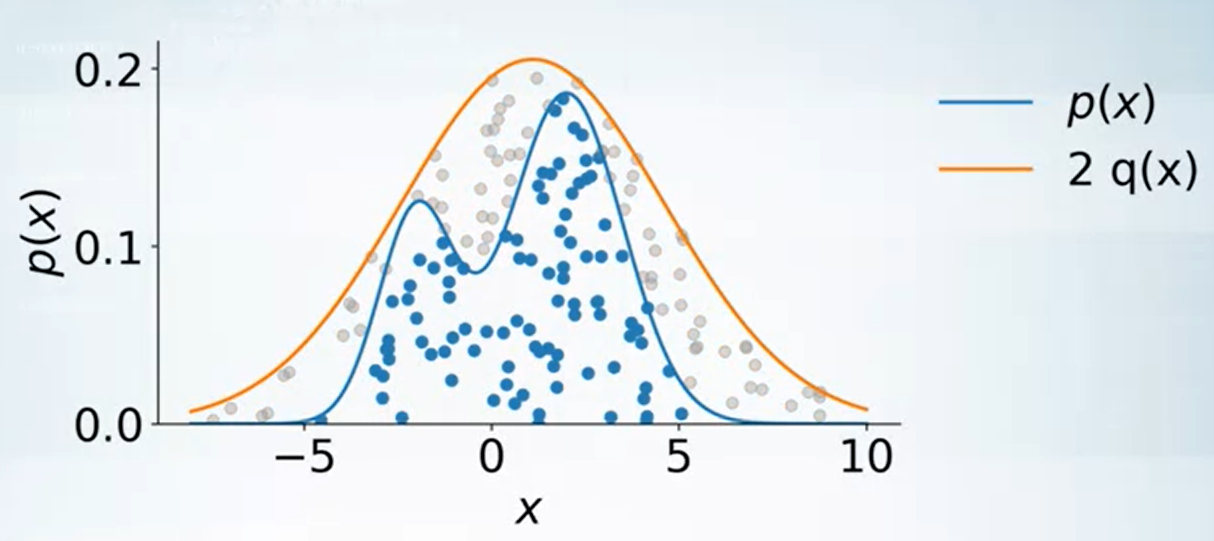
從上面的說明可以看出, accept 的比例其實就是藍色的比例, 因此 upper bound 愈緊密效果愈好.
所以如果 $p(x)\leq Mq(x)$, 則平均 accept $1/M$ points. 這是因為 $p,q$ 都是機率分布, 所以 area under curve 都是 $1$. 因此比例就是 $1/M$.
最後, 這個方法可以用在不知道 normalization term $Z$ 的情形. 例如我們只知道 $\hat{p}(x)$, 但我們仍然可以找到一個 distribution $q(x)$ 乘上 constant $\tilde{M}$ 後是 upper bound:
總解一下此法

結論就是雖然對大部分 distribution 都可以用, 但效率不好. 尤其在維度高的時候會大部分都 reject.
那有什麼方法可以對付高維度呢? 下面要介紹的 MCMC with Gibbs/Metropolis-Hastings 就能處理.
Markov Chains Monte Carlo
這裡假設大家已經熟悉 Markov chain 了, 不多做介紹.
使用 Markov chain 的策略為以下幾個步驟:

重點在如何設計一個 Markov chain (這裡等同於設計 transition probability $T$), 收斂的 stationary distribution 正好就是我們要的 $p(x)$
首先不是每個 Markov chain 都會收斂, 但有一些充分條件如下圖 Theorem:

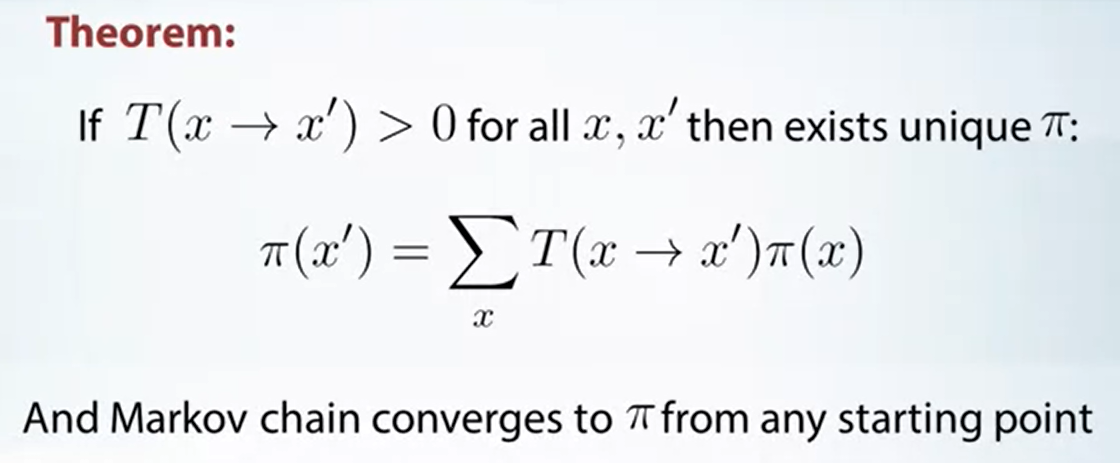
對照 Stochastic Processes 裡的筆記 (之後補 link), 這裡的 theorem 隱含了此 Markov chain 為 ergodic, i.e. 1-equivalence class, recurrent, and aperiodic. 而 ergodic Markov chain 必定存在 stationary distribution.
Gibbs sampling
上面提到使用 Markov chain 取 sample 的話, 怎麼樣的 $T$ 會讓它收斂到 desired $p(x)$
Gibbs sampling 可以想成一種特殊的 $T$ 的設計方法, 可以確保收斂至 $p(x)$
假設我們有一個 3-dim 的 P.D.F., 可以不知道 normalization term $Z$:
從 $(x_1^0, x_2^0, x_3^0)$ 開始, e.g. $(0,0,0)$
先對第一維取 sample:
針對 1-d distribution 取 sample 是很容易的, 可以使用上一節的做法
接著對第二維取 sample:
最後對第三維取 sample:
$$\begin{align} x_3^1 \sim p(x_3 | x_1=x_1^{\color{red}{1}}, x_2=x_2^{\color{red}{1}}) \end{align}$$以上便是一次的 iteration, 所以:
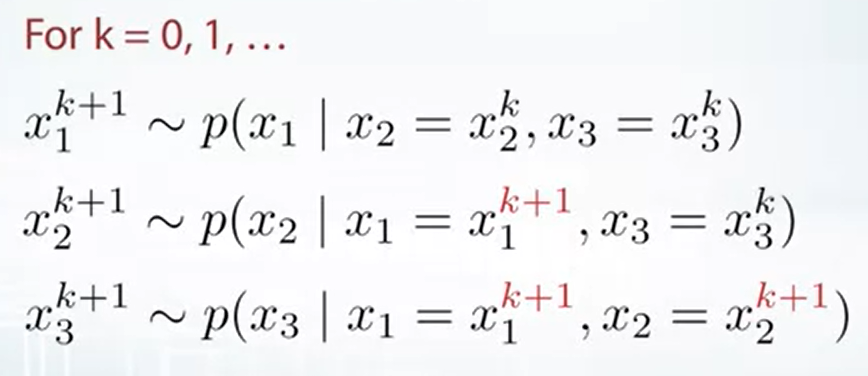
顯而易見, 這個方法不能 parallel, 之後會說怎麼加速 (利用 Metropolis-Hastings)
證明收斂至 desired distribution
現在要證明這樣的採樣方式定義了一個 Markov chain 且會收斂到 desired distribution $p(x)$, which is stationary!
Markov chain 的 states 定義為 $p(x)$ 的 domain, 我們以 $n$-dim 來說就是 $(x_1,x_2,…,x_n)$
Transition probabilities $p_T(x\rightarrow x’)$ , i.e. 從 state $x$ 到 $x’$ 的機率, 使用 Gibbs sampling 來定義:
這裡我們做個假設, 令 $p_T(x\rightarrow x’)>0,\forall x,x’$, 則由定理知道此 Markov chain 必 $\exists !$ stationary distribution. 所以現在問題是該 stationary distribution 是我們要的 $p(x)$ 嗎?
要證明 $p(x)$ 是 stationary, 我們只需證明:
這表示 $p(x)$ 經過 1-step transition 後, 分布仍然是 $p(x)$
所以再來就是用 $p_T(x\rightarrow x’)$ 代入, 驗證看看對不對
觀察 $(\star)$ 到 $(\square)$, 是消耗掉 $x_2$ 的 summantion, 同時也消耗掉對 $x_2$ 的 gibbs sampling step. 因此我們可以對 $(\square)$ 做一樣的事情, 去消耗掉 $x_3$ 的 summantion 以及對 $x_3$ 的 gibbs step.
重複做會得到:
Q.E.D.
總結
大致上有兩個前提:
- 固定其他維度, 對某一維度取 samples 是很容易的
- $p(x_i|x_1,...,x_{i-1}, x_{i+1}, ..., x_n)>0$, 這保證了我們透過 Gibbs sampling 產生的 Markov chain 一定收斂到 desired $p(x)$
優點為:
- 將 multi-dimensional sampling 化簡為 1-d sampling
- 容易實作
缺點為:
- Highly correlated samples, 這使得我們跑到 stationary distribution 後, 也不能連續的取 sample 點
- Slow convergence (mixing)
- Not parallel (接下來介紹的 Metropolis Hastings 幫忙可以改善)
Metropolis-Hastings
Gibbs sampling 缺點是 samples are too correlated, 且不能平行化. 注意到在 Gibbs sampling 方法裡, 已經定義好某一個特別的 Markov chain 了. Metropolis-Hastings 則可以定義出一個 famliy of Markov chain 都收斂到 desired distribution. 因此可以選擇某一個 Markov chain 可能收斂較快, 或是 less correlated.
Metropolis-Hastings 中心想法就是 “apply rejection sampling to Markov chains”
Algorithm

其中 $Q(x^k\rightarrow x)$ 是任意事先給定的一個 transition probabilities (注意到需滿足 $>0,\forall x,x’$, 這樣才能保證唯一收斂)
$A(x^k\rightarrow x)$ 表示 given $x^k$ accept $x$ 的機率, 稱為 critic
演算法流程為: 先從 $Q(x^k\rightarrow x)$ 取樣出 $x’$, $x’$ 有 $A(x^k\rightarrow x’)$ 的機率被接受, 一旦接受則 $x^{k+1}=x’$ 否則 $x^{k+1}=x^k$, 然後 iterate 下去
使用這種方式的話, 我們其實可以算出 transition probability $T(x\rightarrow x’)$, 如上圖
所以關鍵就是, 怎麼選擇 $A(x^k\rightarrow x)$ 使得這樣的 Markov chain 可以收斂到 desired probability $\pi(x)$
怎麼選擇 Critic $A$ 使得 Markov chain 收斂到 $\pi$
我們先介紹一個充分條件 (所以有可能 $\pi(x)$ 是 stationary 但是不滿足 detailed balance equation)
[Detailed Balance Equation]:
若 $\pi(x)T(x\rightarrow x’)=\pi(x’)T(x’\rightarrow x), \forall x,x’$, 則 $\pi(x)$ 為 stationary distribution, i.e. $\pi(x')=\sum_x \pi(x)T(x\rightarrow x')$
[Proof]:
$$\begin{align} \sum_x \pi(x)T(x\rightarrow x') \\ \text{by assumption} = \sum_x \pi(x')T(x'\rightarrow x) \\ = \pi(x')\sum_x T(x'\rightarrow x) = \pi(x') \end{align}$$所以只要選擇的 $A(x\rightarrow x’)$ 能夠讓 $T(x\rightarrow x’)$ 針對 $\pi(x)$ 滿足 detailed balance 特性就能保證 Markov chain 收斂到 $\pi(x)$
因此我們計算一下, 只需考慮 $x\neq x’$ 的情形 (因為 $x=x’$ 一定滿足 detailed balance equation, 這不是廢話嗎)
所以當 $\rho<1$ 我們設定
$$\begin{align} \left\{ \begin{array}{r} A(x\rightarrow x')=\rho \\ A(x'\rightarrow x)=1 \end{array} \right. \end{align}$$而如果 $\rho>1$ 我們設定
$$\begin{align} \left\{ \begin{array}{r} A(x\rightarrow x')=1 \\ A(x'\rightarrow x)=1/\rho \end{array} \right. \end{align}$$總結來說 $A$ 可以這麼設定
$$\begin{align} A(x\rightarrow x')=\min\left\{ 1, \frac{\pi(x')Q(x'\rightarrow x)}{\pi(x)Q(x\rightarrow x')} \right\} \end{align}$$注意到 $\rho$ 是可以直接算出來的, 因為 $Q,\pi$ 都是事先給定已知的, 因此我們就能設定出對應的 acceptance distribution $A$.
同時如果我們只有 unnormalized distribution, i.e. $\hat\pi(x)$, 由 $A$ 的設定可以看出不受影響
$$\begin{align} A(x\rightarrow x')=\min\left\{ 1, \frac{ {\color{orange}{\hat\pi(x')}} Q(x'\rightarrow x)}{ {\color{orange}{\hat\pi(x)}} Q(x\rightarrow x')} \right\} \end{align}$$怎麼選擇 $Q$
首先需滿足 $Q(x\rightarrow x’)>0,\forall x,x’$. 這樣才會有以上的推論.
$Q$ 會希望能走”大步”一點, 也就是 transition 不要只圍繞在相鄰的點. 好處是產生的 sample 會比較無關.
但如果走太大步, critic $A$ 就有可能一直 reject (why?) 導致效率太差
想像如果 $x$ 已經在機率很高的地方了, 例如 local maximum point. 如果 $Q$ 走太大步到 $x’$, 則容易 $\pi(x’)<<\pi(x)$, 造成 $A$ 太小容易 reject
所以如果 $Q$ 走小步一點, $x’$ 還是圍繞在 $x$ 附近, 相對來說可能機率就不會那麼低
Example of Metropolis-Hastings
1-d case toy example
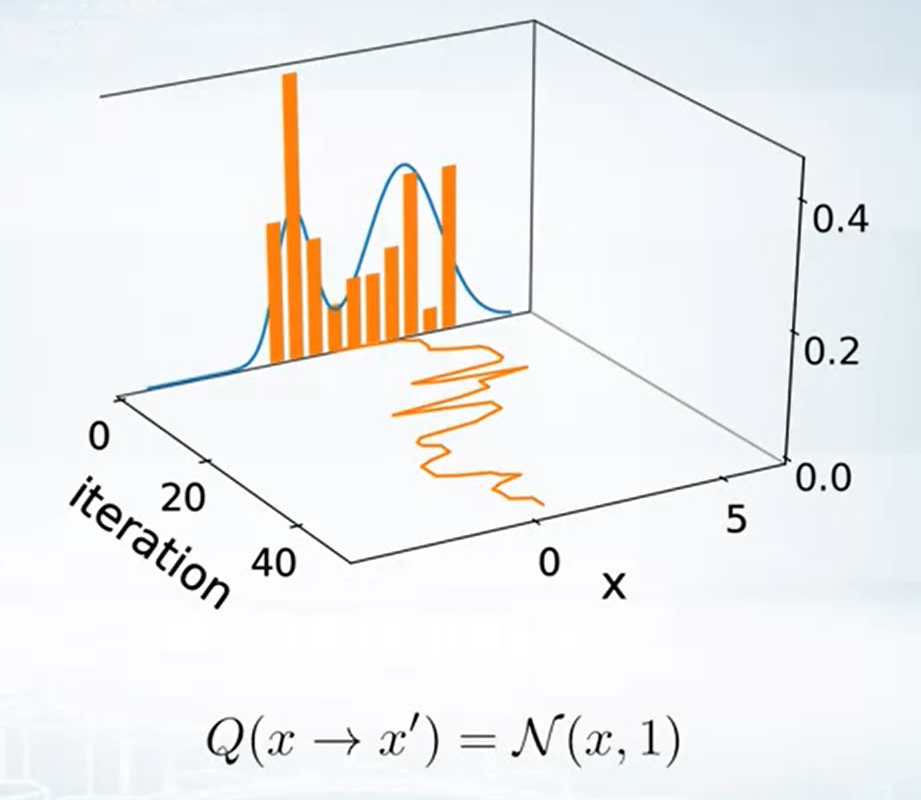
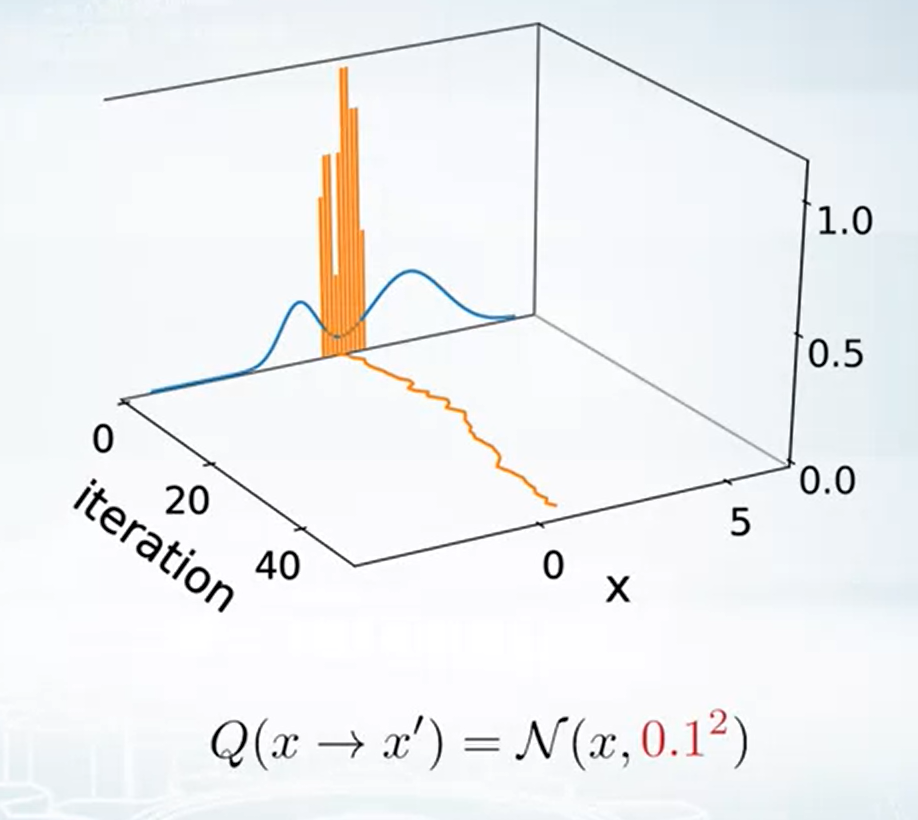
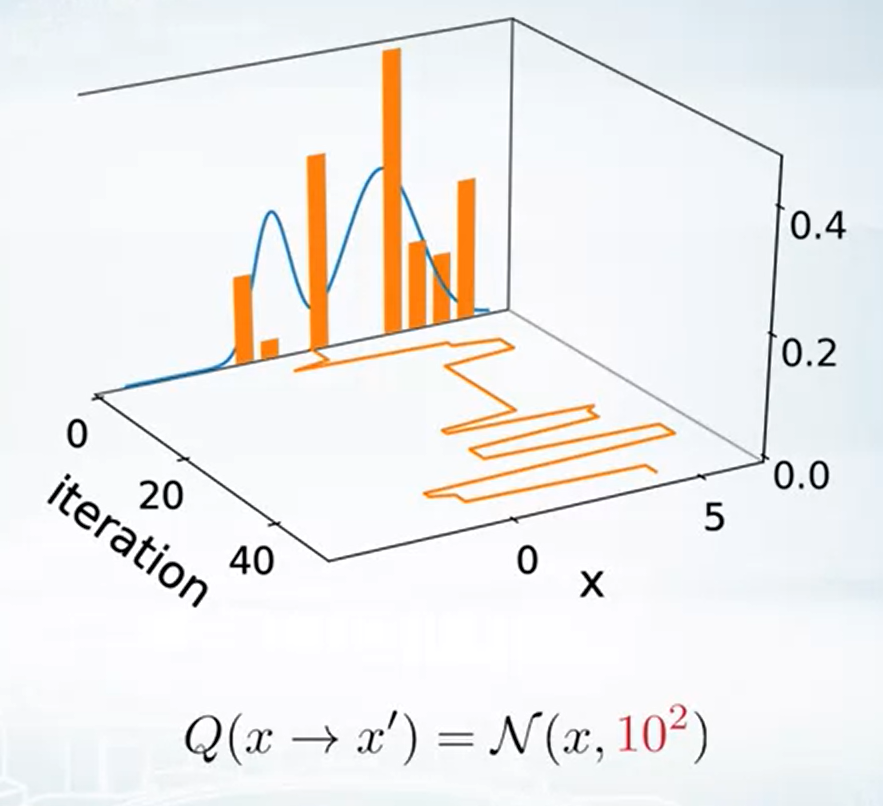
告訴我們 proposal 的 distribution 選擇也是很重要的.
最後可以使用 Metropolis Hastings 來平行化 Gibbs sampling!
我們使用如下圖 “錯誤的” Gibbs sampling 方法, 並將這方法視為 Metropolis Hastings 的 proposal $Q(x\rightarrow x’)$
因此可以平行對每個維度取 sample! (好聰明!)

結語
MCMC 被譽為 20 世紀十個偉大的演算法發明之一 [3]. 找知乎的文章可以看到這個討論: 有什么理论复杂但是实现简单的算法?[4] 果然 MCMC 理論不是一般人能做的.
後續對於 Metropolis-Hastings 的改進有一個算法是 Metropolis-adjusted Langevin algorithm [5] (MALA). 該方法提出使用 Langevin dynamics [6] 當作 proposal, 這會使得 random walk 會走向機率比較高的地方, 因此被拒絕機率較低. 但是 MALA 我實在看不懂, 只知道跟 Langevin dynamics sampling [7] 有關
在 Generative Modeling by Estimating Gradients of the Data Distribution [8] 的 Langevin dynamics 段落裡提到 MALA 可以只根據 score function ($\nabla_x \log p(x)$) 就從 P.D.F. $p(x)$ 取 samples!
會看到 MALA 是因為除了 GAN 之外最近很熱門的 generative models: DPM [9]), 其核心技術之一用到它.
看來要全部融會貫通目前會先卡關在這了. MALA 你等著! 別跑啊, 不要以為我怕了你, 總有一天我 #$@^#@$Q (逃~)
Appendix
證明 $var[\hat f]=\frac{1}{L}Var(f)$ 如下:
首先兩個 independent r.v.s $X,Y$ 我們知道其 covariance 為 $0$:
$$\begin{align} 0 = Cov[XY] = \mathbb{E}\left[ (X-\mu_x)(Y-\mu_y) \right] \\ = \mathbb{E}[XY-X\mu_y-\mu_xY+\mu_x\mu_y] = \mathbb{E}[XY] - \mu_x\mu_y \\ \Rightarrow \mathbb{E}[XY] = \mu_x\mu_y \ldots(\star) \end{align}$$且有 variance 的性質: $Var(X)=\mathbb{E}[X^2]-\mu_x^2\ldots(\star\star)$
接著開始計算:
Reference
- Curse of Dimensionality — A “Curse” to Machine Learning
- Coursera: Bayesian Methods for Machine Learning
- The Best of the 20th Century: Editors Name Top 10 Algorithms
- 有什么理论复杂但是实现简单的算法?
- Metropolis-adjusted Langevin algorithm: wiki
- Langevin dynamics: wiki
- 抽样理论中有哪些令人印象深刻(有趣)的结论?
- Generative Modeling by Estimating Gradients of the Data Distribution
- What are Diffusion Models?