Sharp V.S. Flat Local Minimum 的泛化能力
先簡單介紹這篇文章:
On large-batch training for deep learning: Generalization gap and sharp minima
考慮下圖兩個 minimum, 對於 training loss 來說其 losses 一樣.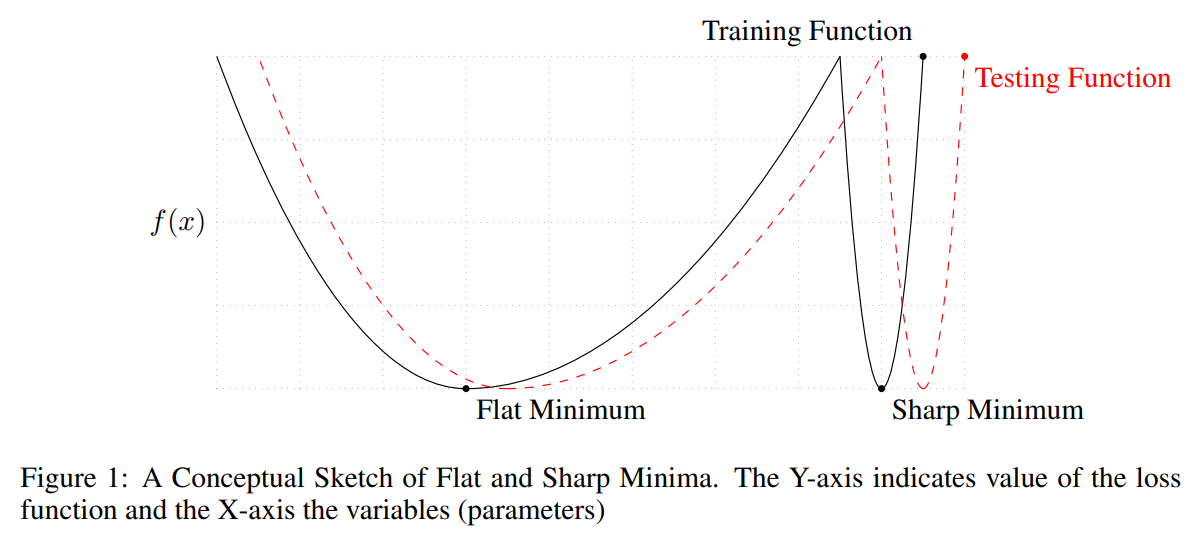
從圖可以容易理解到, 如果找到太 sharp 的點, 由於 test and train 的 mismatch, 會導致測試的時候 data 一點偏移就會對 model output 影響很大.
論文用實驗的方式, 去評量一個 local minimum 的 sharpness 程度, 簡單說利用 random perturb 到附近其他點, 然後看看該點 loss 變化的程度如何, 變化愈大, 代表該 local minimum 可能愈 sharp.
然後找兩個 local minimums, 一個估出來比較 sharp 另一個比較 flat. 接著對這兩點連成的線, 線上的參數值對應的 loss 劃出圖來, 長相如下: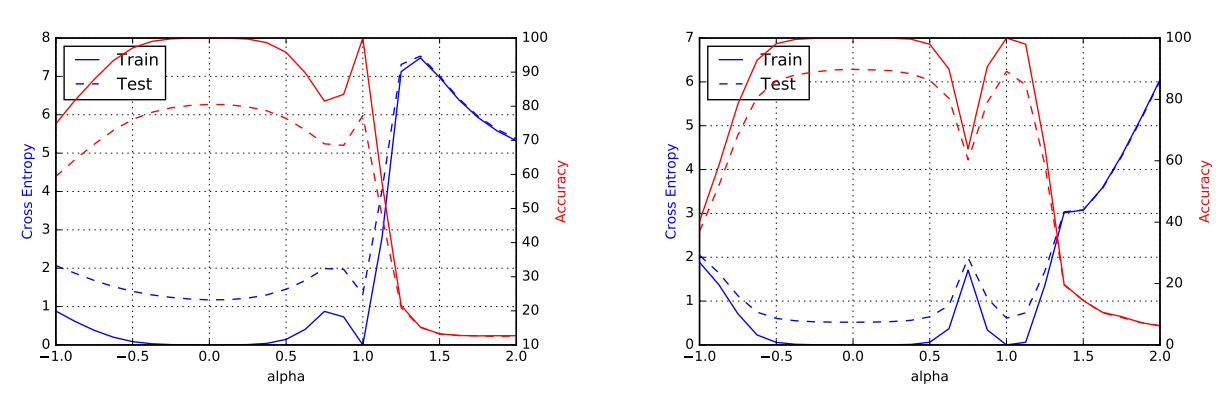
這也是目前一個普遍的認知: flat 的 local minimum 泛化能力較好.
所以可以想像, step size (learning rate) 如果愈大, 愈有可能跳出 sharp minimum.
而 batch size 愈小, 表示 gradient 因為 mini-batch 造成的 noise 愈大, 相當於愈有可能”亂跑”跑出 sharp minimum.
但這篇文章僅止於實驗性質上的驗證. Step size and batch size 對於泛化能力, 或是說對於找到比較 flat optimum 的機率會不會比較高? 兩者有什麼關聯呢?
DeepMind 的近期 (2021) 兩篇文章給出了很漂亮的理論分析.
Full-Batch Gradient (Steepest) Descent
再來介紹這篇: Implicit Gradient Regularization, DeepMind 出品.
想探討為什麼 NN 的泛化能力這麼好? 結論就是跟 Gradient Descent 本身算法特性有關.
一般我們對 cost (loss) function 做 gradient (steepest) descent 公式如下:
其中 $h$ 為 step size (learning rate), $\omega\in\mathbb{R}^d$ 表示 parameters.
當 $h\rightarrow 0$, $n$ 變成連續的時間 $t$, 則可視為一個 Ordinary Differential Equation (ODE) system, 整理如下:
$$\begin{align}
\text{Cost Function}: C(\omega) \\
\text{ODE}: \dot{\omega}=f(\omega)=-\nabla C(\omega)
\end{align}$$
給定 initial point $\omega_0$, 上面的 ODE 求解就是一條連續的 trajectory.
💡 我們在 Numerical Methods for Ordinary Differential Equations 有介紹各種數值方法, 可以知道 gradient descent 就是 Euler method, 而這樣的 error 是 $O(h^2)$.
用式 (1) gradient descent ($h$ 固定) 求解, 會使得 trajectory 跟連續的 ODE (3) 的不同.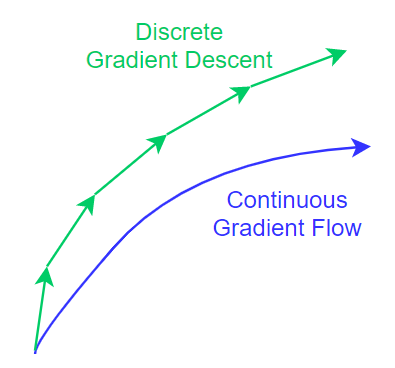
注意到這裡沒有使用 mini-batch, 用的是 full-batch, 所以不是 Stochastic gradient descent (SGD).
如果我們能對 gradient descent 的 trajectory 用另一個 ODE system 的 trajectory 代表的話 (怎麼找等等再說), 分析修改過後的 ODE 和原來的 ODE systems 說不定能看到什麼關聯. 這正是這篇論文的重要發現.
先來看看修改過後的 ODE 長什麼樣:
$$\begin{align}
\text{Cost Function}: \tilde{C}_{gd}(\omega)=C(\omega)+\frac{h}{4}\|\nabla C(\omega)\|^2 \\
\text{ODE}: \dot{\omega}=\tilde{f}(\omega)=-\nabla\tilde{C}_{gd}(\omega)
\end{align}$$
注意到最佳解與原來的 ODE system 一樣: $C(\omega)$ 和 $\tilde{C}_{gd}(\omega)$ 最佳解相同. (很容易可以看出來因為 minimal points 其 gradient 必定為 $0$)
將三條 trajectories 用圖來表示的話如下:
- Gradient descent 的 trajectory 式 (1): 綠色箭號線
- ODE 的 trajectory 式 (3): 黑色線
- 修改後的 ODE 的 trajectory 式 (5): 黃色線, 可以用來代表 gradient descent 的 trajectory
(參考自 inFERENCe blog 文章: Notes on the Origin of Implicit Regularization in SGD)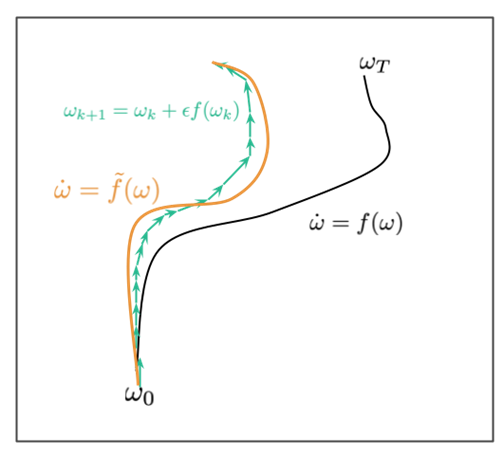
為什麼可以用修改後的 ODE 代表 gradient descent 的 trajectory 呢?
因為兩者差異夠小, 為 $O(h^3)$, 比 gradient descent 和原本 ODE 之間的 error $O(h^2)$ 更小.
(綠色箭號線比起黑色線更接近黃色線)
再來我們回答這個問題: 怎麼找到 (4) (5) 這樣的 ODE 可以用來代表 gradient descent 的 trajectory 呢?
💡 需利用 backward error analysis, 這裡略過, 請參考 [ref1] [ref2]
其中 ref2 裡的二階 Taylor expansion 補充推導:
$$\left.\frac{d^2}{dt^2}\tilde{y}(t)\right|_{t=t_n}=\left.\frac{d}{dt}\left[ f(\tilde{y}(t))+hf_1(\tilde{y}(t)) \right]\right|_{t=t_n} \\ =\left.\left[ f'(\tilde{y}(t))\frac{d\tilde{y}(t)}{dt}+hf_1'(\tilde{y}(t))\frac{d\tilde{y}(t)}{dt} \right]\right|_{t=t_n} \\ =\left.\left[ f'(\tilde{y}(t))\tilde{f}(\tilde{y}(t))+hf_1'(\tilde{y}(t))\tilde{f}(\tilde{y}(t)) \right]\right|_{t=t_n} \\ =\left.\left[ \left( f'(\tilde{y}(t))+hf_1'(\tilde{y}(t)) \right)\tilde{f}(\tilde{y}(t)) \right]\right|_{t=t_n} \\ =(f'(\tilde{y}_n)+hf_1'(\tilde{y}_n))\tilde{f}(\tilde{y}_n)$$
觀察 (4) 的 $\tilde{C}_{gd}(\omega)$, 可以發現相當於在原來的 cost function $C(\omega)$ 加上一個正則項. 而該項正比於 gradient norm 的平方.
白話就是如果 gradient 愈大, penalty 愈大, 所以優化的時候會傾向於找 gradient 小的區域. 相當於找比較 flat 的區域. 這樣有什麼好處呢? 如同一開始說的, 能提高泛化能力!
另外正則項也正比於 step size $h$, 所以如果 step size 愈大, 表示對 sharp 區域的 penalty 愈大, 因此更加傾向找 flat 區域. 這也符合我們之前提到愈有可能跳出 sharp minimum 的觀點. 另外作者的 presentation 開頭也用以下例子說明這個現象: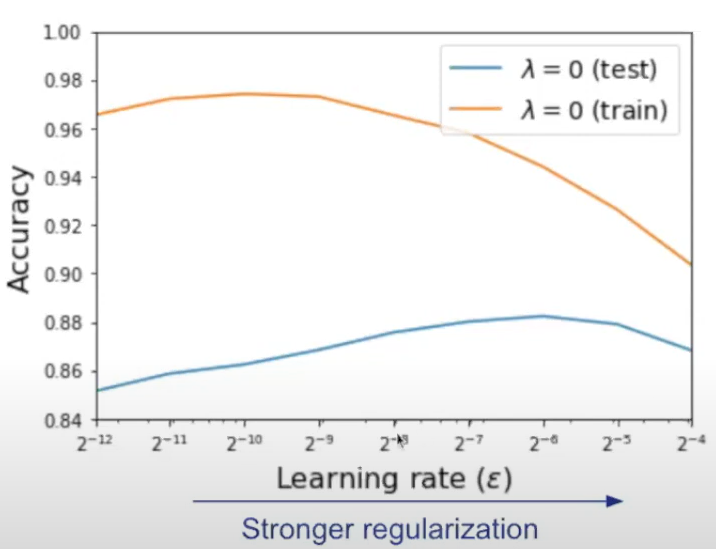
大的 learning rate 傾向找比較 flat 的 minimum, 也就是泛化能力較好. 所以對應到上圖顯示的 Test 情況下最好的 learning rate 比 training 的要大.
總結來說提供了一個看法, 說明為什麼 NN 的表現這麼好, 特別是泛化能力. 很意外的是, 其實跟我們用的 gradient descent 天生的特性有關.
Mini-Batch Stochastic Gradient Descent
上一段都還沒考慮 mini-batch 的情況. 因為一旦變成 mini-batch 相當於 gradient 被加上了 random noise 變的更難分析. 因此 DeepMind 他們發了一篇後續文章: On the Origin of Implicit Regularization in Stochastic Gradient Descent, 將 mini-batch 考量進去, 相當於分析 SGD 算法.
由於 mini-batches 在一個 epoch 可能的順序不一樣, 所以一條 trajectory 對應到一個順序.
(參考自 inFERENCe blog 文章: Notes on the Origin of Implicit Regularization in SGD)
我們變成要考量的是 “mean” trajectory. 類似地, mean trajectory 一樣可以用一個修改後的 ODE system 來代表它:
$$\begin{align}
\text{Mean Trajectory}: \mathbb{E}(\omega_m)=\omega(mh)+O(m^3h^3)\\
\text{Cost Function}:\tilde{C}_{sgd}(\omega)= \tilde{C}_{gd}(\omega) +
\underbrace{\frac{h}{4m}\sum_{i=0}^{m-1}\|\nabla \hat{C}_i(\omega)-\nabla C(\omega)\|^2}_\text{additional regularizer} \\
\text{ODE}: \dot{\omega}=-\nabla\tilde{C}_{sgd}(\omega)
\end{align}$$
其中 $m$ 表示整個 training data 可以分成 $m$ 個 mini-batches. $\nabla \hat{C}_i(\omega)$ 表示 i-th mini-batch 的 gradient.
可以看到多了一項正則項: mini-batches 的 gradients 減掉 full-batch gradient 的 variance.
我們就先當 $\omega$ 已經是 local minimum 好了 ($\nabla C(\omega)=0$). 所以該正則項簡化成 mini-batches gradients 的 variance.
相當於告訴我們, 如果 mini-batches 的那些 gradients 差異都很大的話, penalty 會比較大, 比較不會是 SGD 會找到的解.
這樣的特性對於泛化能力有什麼關聯? inFERENCe 文章給了一個很清楚的說明:
x-軸是 parameter $\omega$, y-軸是 loss $C(\omega)$.
Variance of mini-batches’ gradients 左圖比右圖小, 因而造成右圖的 penalty 比較大, 所以 (8) 會傾向選擇左圖. 明顯的, 對於 test data 來說左圖的解會比右圖 robust, 因為 test data 可以看成上面不同 batches 的表現.
可以從 (7) 看出來, 由於 additional regularizer 的關係, SGD 最佳解會跟原來 full-batch 的最佳解不同了. 除非所有 mini-batches 的 gradients 也都是 $0$.
另外 (7) 在論文中也推導成另一個形式 (對比(7)為 additional regularizer 改寫了):
$$\mathbb{E}(\tilde{C}_{sgd}(\omega))=\tilde{C}_{gd}(\omega)+\frac{N-B}{N-1}\frac{\color{orange}{h}}{4\color{orange}{B}}\Gamma(\omega) \\
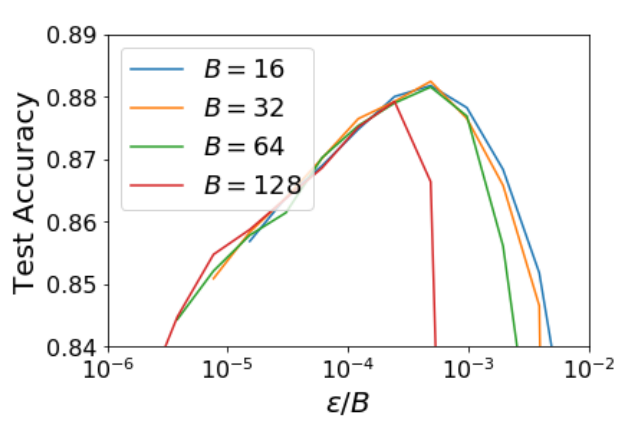
\Gamma(\omega)=\frac{1}{N}\sum_{i=1}^N \|\nabla C_i(\omega)-\nabla C(\omega)\|^2$$ 可以看出 learning rate and batch size 的關係, $h/B$ 如果維持一定比例, 則正則項的影響力大約相同.
作者 presentation 說, 經驗上 batch size double, learning rate 也要 double. [YouTube time]
對應到 $h/B$ 比例不變, 所以 performance 應該也維持一樣 (在 $B$ 不大的情況下). 論文做了實驗結果如下:
結論
雖然存在一些假設才會使 SGD 的估計正確
⚠️ 論文推導的假設:
- batch shuffle 的方式取 data, 也就是一個 epoch 會依序跑完 shuffle 後的所有 batches
- learning rate is finite (就是有 lower bound)
- 只分析 SGD, 其他更多變形例如 Adam, Adagrad, RMSProp, 等的行為不知道
- $m^3h^3$ 必須要夠小, SGD 的 “mean” trajectory 才會符合 (7), (8) 的 ODE 結果. 一般 dataset 都很大 ($m$ 很大), 所以要把 $h$ 都設定很小, 感覺也有點難符合 (?). 影片: [here]
但總結來說, 在 full-batch 設定下, 實務上使用 steepest descent 從連續變成離散的路徑, 本身就提供了泛化能力的好處. 加上 mini-batch 的設定, 使得泛化能力更好了.
沒想到已經習以為常的 SGD 方法, 背後竟然藏了這樣的觀點, 太厲害了!
References
- Implicit Gradient Regularization
- On the Origin of Implicit Regularization in Stochastic Gradient Descent
- inFERENCe: Notes on the Origin of Implicit Regularization in SGD
- Numerical Methods for Ordinary Differential Equations
- On large-batch training for deep learning: Generalization gap and sharp minima
- Paper presentation by author: On the Origin of Implicit Regularization in Stochastic Gradient Descent