如果對於 Differential Equation 完全沒概念, 建議先看以下兩分鐘的影片
- Solving Differential Equations vs. Solving Algebraic Equations
主要筆記了 Prof. Jeffrey Chasnov 在 Coursera 的兩門課 針對 numerical solution 解 ODE 的內容:
1. Differential Equations for Engineers
2. Numerical Methods for Engineers
本文介紹:
1️⃣ Introduction to ODE: linear? ordinary? n-th order?
2️⃣ Euler Method: 雖然簡單, 但 error 很大
3️⃣ Modified Euler Method: error $O(\Delta t^3)$, 比 Euler method 小了一個 order
4️⃣ Runge Kutta Methods: Modified Euler 方法是 Second-order RK 的一個特例
5️⃣ Higher-order Runge-Kutta Methods: $n$-th order RK 的 error 為 $O(\Delta t^{n+1})$
6️⃣ Higher-order ODEs and Systems: 以上都只介紹 first-order ODE 逼近法, 那 higher-order ODE 怎解?
👏 那兩門課的講義教授很佛心得都有附上:
Lecture notes: Differential Equations for Engineers
Lecture notes: Numerical Methods for Engineers
1️⃣ Introduction to differential equations | Lecture 1 | Differential Equations for Engineers
[YouTube]
$$\begin{align}
L\frac{d^2q}{dt^2}+R\frac{dq}{dt}+\frac{1}{C}q=\varepsilon_0\cos wt \\
ml\frac{d^2\theta}{dt^2}+cl\frac{d\theta}{dt}+mg\sin\theta=F_0\cos wt \\
\frac{\partial u}{\partial t}=D\left(\frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2}+\frac{\partial^2u}{\partial z^2}\right)
\end{align}$$
其中 $q=q(t)$, $\theta=\theta(t)$, $u=u(x,y,z,t)$
全部都是 $2^{\text{nd}}$-order, 因為 independent variable $x,y,z,t$ 的微分最高 order 等於 2.
(1) and (2) 是 ordinary differential equation (ODE)
(3) 是 partial differential equation (PDE)
(1) and (3) 是 linear, (2) 是 nonlinear, 因為有 $\sin\theta$.
Linear 指的是要微分的那個 function (i.e. $q,\theta,u$) 不管有沒有要微分, 都不能過一個 nonlinear function, 例如 $d(q^2)/dt$ 這樣就不行 (平方是 nonlinear function), 或沒有要微分, 直接 $q^2$ 也不行.
Linear N-order ODE/PDE 有解析解, 所以 “Differential Equations for Engineers” 這門課主要講這部分.
不過如果是 non-linear $n^\text{th}$-order ODE 雖沒有解析解, 但可利用以下介紹的 numerical methods 求近似解.
The general linear third-order ode, where $y=y(x)$:
$$a_3(x)y'''+a_2(x)y''+a_1(x)y'+a_0(x)y=b(x)$$ where the $a$ and $b$ coefficients can be any function of $x$.
2️⃣ Euler method | Lecture 2 | Differential Equations for Engineers | Lecture 48 | Numerical Methods for Engineers
[YouTube] [YouTube]
討論一個 first-order ode (不只 linear, 也包含 non-linear, 所以一般沒有 analytical solution) 的逼近求解方法.
這裡說包含 nonlinear 是因為 $f(x,y)$ 有可能使的 function $y=y(x)$ 會變成 nonlinear
$$\frac{dy}{dx}=f(x,y) \\
y(x_0)=y_0$$ 用 numerical method 去逼近.

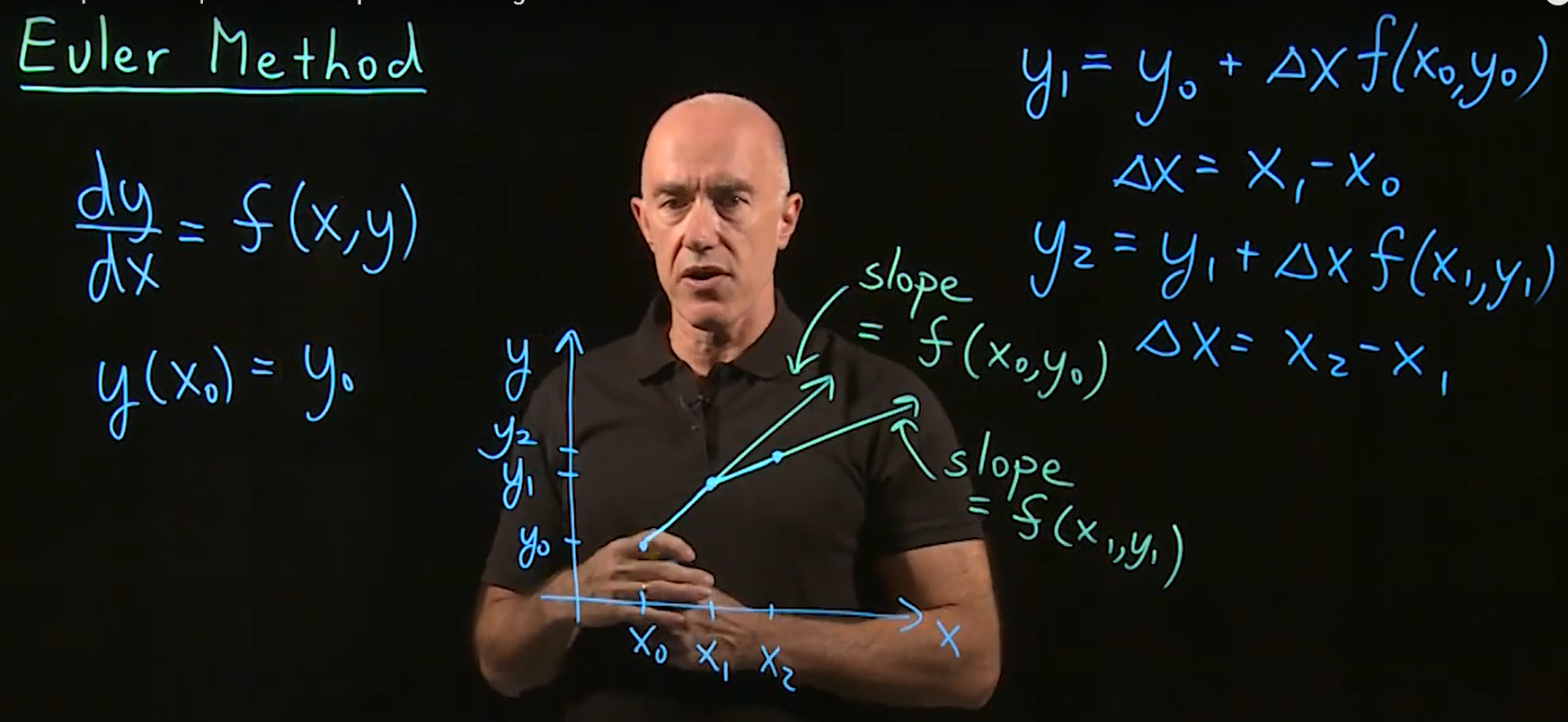
Euler method 是 first order method.
3️⃣ Modified Euler Method | Lecture 49 | Numerical Methods for Engineers
[YouTube]
原來的 Euler method 要計算 $x_{n+1}$ 的時候用下式逼近
$$x_{n+1}=x_n+\Delta t\underbrace{f(t_n,x_n)}_\text{slope}$$ 但可以看到 slope 其實一直在變化. 如果說 slope 改成用 $f(t_n,x_n)$ and $f(t_n+\Delta t,x_{n+1})$ 的平均呢?
這就是 Modified Euler Method 主要想法.
💡 Modified Euler Method 屬於 $2^\text{nd}$-order Runge-Kutta Methods (RK2) 的一種.
下段介紹 RK 方法時會推導可以知道確實 error order 會比較小
注意到 Runge-Kutta 說的 order 指 error 的 order, 跟 ODE 的 order 代表 independent variable 的最高次數微分意思不一樣.
但我們不知道 $x_{n+1}$ 要怎麼算 $f(t_n+\Delta t,x_{n+1})$ 呢? 所以就先算一個 $x_{n+1}$ 的 prediction.
$$\begin{align} x_{n+1}^p=x_n+\Delta tf(t_n,x_n) \\ x_{n+1}=x_n+\frac{\Delta t}{2}\left[f(t_n,x_n)+f(t_n+\Delta t,x_{n+1}^p)\right] \end{align}$$可以簡化一下變成下面幾個 stages:
$$\begin{align}
K_1=\Delta t f(t_n,x_n) \\
K_2=\Delta tf(t_n+\Delta t,x_n+K_1) \\
x_{n+1}=x_n+\frac{1}{2}(K_1+K_2)
\end{align}$$
4️⃣ Runge Kutta Methods | Lecture 50 | Numerical Methods for Engineers
[YouTube]
對一個 first order ODE, 且已知 $x(t_n)=x_n$ initial value 來說
$$\dot{x}=f(t,x)$$ 經過時間 $\Delta t$ 後的 $x(t_n+\Delta t)$ 要怎麼估計比較準? 我們先看 Taylor expansion:
$$\begin{align}
x(t_n+\Delta t)=x(t_n)+\Delta tf(t_n,x_n)+\frac{(\Delta t)^2}{2}\left.\frac{d}{dt}f(t,x(t)) \right|_{t=t_n} + O(\Delta t^3)
\end{align}$$ 二次微分項我們用 chain rule 繼續展開:
$$\left.\frac{d}{dt}f(t,x(t))\right|_{t=t_n}=\left.\frac{\partial}{\partial t}f(t,x)\right|_{t=t_n} +
\left.\frac{\partial}{\partial x}f(t,x(t))\frac{dx}{dt}\right|_{t=t_n} \\
= \frac{\partial}{\partial t}f(t_n,x_n) + \left.\frac{\partial}{\partial x}f(t,x(t))f(t,x(t))\right|_{t=t_n} \\
= \frac{\partial}{\partial t}f(t_n,x_n) + \frac{\partial}{\partial x}f(t_n,x_n)f(t_n,x_n) \\
\triangleq f_t(t_n,x_n)+f_x(t_n,x_n)f(t_n,x_n)$$
代回去 (9) 得到 $x(t_n+\Delta t)$ 的泰勒展開式:
$$\begin{align} x(t_n+\Delta t)=x_n+\Delta tf(t_n,x_n) + \frac{(\Delta t)^2}{2}(f_t(t_n,x_n)+f_x(t_n,x_n)f(t_n,x_n)) + O(\Delta t^3) \end{align}$$ Second order Runge-Kutta methods 的步驟如下:$$\begin{align} K_1=\Delta tf(t_n,x_n) \\ K_2=\Delta tf(t_n+\alpha\Delta t,x_n+\beta K_1) \\ x_{n+1}=x_n+aK_1+bK_2 \end{align}$$ 全部合成一個式子:
$$\begin{align} x_{n+1}=x_n+a\Delta tf(t_n,x_n)+b\Delta t \underbrace{f(t_n+\alpha\Delta t,x_n+\beta \Delta tf(t_n,x_n))}_\text{using Taylor expansion} \\ =x_n+a\Delta tf(t_n,x_n)+b\Delta t \left[ f(t_n,x_n) + \alpha\Delta t f_t(t_n,x_n)+\beta\Delta tf(t_n,x_n)f_x(t_n,x_n) + O(\Delta t^2) \right] \\ = x_n+(a+b)\Delta tf(t_n,x_n)+(\Delta t)^2 \left[ \alpha b f_t(t_n,x_n) + \beta bf(t_n,x_n)f_x(t_n,x_n) \right]+O(\Delta t^3) \end{align}$$
💡 補充一下 (14) 的 Taylor expansion:
$$f(t_n+\Delta t,x_n+\Delta x)=f(t_n,x_n)+\left[\begin{array}{cc}f_t(t_n,x_n) & f_x(t_n,x_n)\end{array}\right]\left[\begin{array}{c}\Delta t \\ \Delta x\end{array}\right] + O\left( \left\| \left[\begin{array}{c}\Delta t \\ \Delta x\end{array}\right] \right\|^2 \right) \\ =f(t_n,x_n)+\Delta t f_t(t_n,x_n) + \Delta x f_x(t_n,x_n) + O(\Delta t^2 + \Delta x^2)$$
不管 $O(\Delta t^3)$ 項的情況下, 令 $x(t_n+\Delta t)=x_{n+1}$, i.e. (10)=(16) , 得到:
$$\begin{align}
a+b=1 \\
\alpha b=\frac{1}{2}\\
\beta b=\frac{1}{2}
\end{align}$$ 所以結論就是使用 Second order Runge-Kutta methods 的步驟 (11)-(13), 所產生的 error order 為 $O(\Delta t^3)$.
Check (6)-(8) 的 Modified Euler method 步驟再跟 Second order Runge-Kutta methods 的步驟 (11)-(13) 對比.
很容易可以發現這是 $a=b=1/2,\alpha=\beta=1$ 的情況, 同時也因為滿足 (17)-(19) 的條件, 所以 Modified Euler method 是 Second order Runge-Kutta methods 的一種情況.
另一種 case 是叫 midpoint method: $a=0, b=1, \alpha=\beta=1/2$.
5️⃣ Higher-order Runge-Kutta Methods | Lecture 52 | Numerical Methods for Engineers
[YouTube]
Runge-Kutta Methods 的 order 跟精確度有關, 例如 $n^{th}$-order 表示 error term 只有 $O(\Delta t^{n+1})$ 大小.
💡 給定一個可容忍的 error tolerance $\varepsilon$, 怎麼決定 step size $\Delta t$ 多大, 在 RK4/5 是 ok 的, 這樣的決定方法稱為 Adaptive Runge-Kutta methods. 這邊就不筆記了.
大概了解一下愈高 order 所需要的 stages 愈多
$4^\text{th}$-order 需要 $4$ stages, 但 $5^\text{th}$-order 變成要 $6$ stages. 所以 $4^\text{th}$-order 很不錯, 稱 RK4.
6️⃣ Higher-order ODEs and Systems | Lecture 53 | Numerical Methods for Engineers
[YouTube]
ODE 的 order 指的是 independent variable 的最高微分次數.
例如 $F=ma$ 就是 $2^\text{nd}$-order ODE:
$$F=m\frac{d^2x}{dt^2}$$ 建議直接看 Lecture 53 Higher-order odes and systems.
概念就是 $n^\text{th}$-order ODE 可以拆成 $n$ 個 $1^\text{st}$-order ODEs, 然後當成一個 dimension $n$ 的 vector 來看, 套用 Runge Kutta Methods (RK2, RD4 都可以) 來解.
[Second-order ODE 範例]:
Write down the second-order Runge-Kutta modified Euler method (predictor-corrector method) for the following system of two first-order odes:
$$\dot{x}=f(t,x,y) \\
\dot{y}=g(t,x,y)$$
[Ans:]
我們令 $Z=[x,y]^T$: (符號有點濫用,不過看得懂就可以)
$$\nabla_tZ=[\dot{x}, \dot{y}]^T \\
\nabla_tZ(t_n,Z_n)=[f(t_n,x_n,y_n),g(t_n,x_n,y_n)]^T$$ 對 $Z$ 做 modified Euler method:
$$Z_{n+1}^p=Z_n+\Delta t\nabla_tZ(t_n,Z_n) \\
Z_{n+1}=Z_n+\frac{\Delta t}{2}\left(\nabla_tZ(t_n,Z_n)+\nabla_tZ(t_n+\Delta t,Z_{n+1}^p)\right)$$ 整理成 Runge-Kutta steps:
$$A_1=\Delta t\nabla_tZ(t_n,Z_n) \\
A_2=\Delta t\nabla_tZ(t_n+\Delta t,Z_n+A_1) \\
Z_{n+1}=Z_n+\frac{1}{2}(A_1+A_2)$$ 拆開每個維度來看:
$$A_1=\Delta t[f(t_n,x_n,y_n),g(t_n,x_n,y_n)]^T = [K_1,L_1]^T\\
A_2=\Delta t \left[\begin{array}{cc}
f(t_n+\Delta t,x_n+K_1,y_n+L_1) \\
g(t_n+\Delta t,x_n+K_1,y_n+L_1)
\end{array}\right]
=\left[\begin{array}{c}
K_2\\L_2
\end{array}\right] \\
Z_{n+1}=\left[\begin{array}{cc}
x_{n+1}\\y_{n+1}
\end{array}\right]
=\left[\begin{array}{cc}
x_n+\frac{1}{2}(K_1+K_2) \\ y_n+\frac{1}{2}(L_1+L_2)
\end{array}\right]$$ 結論就是可以拆成兩個 parallel 的 update 步驟, 最後的公式:
🤔 一開始不確定兩個 parallel 的 update 步驟是不是正確的, 因為會互相參照. 但如果當成一個 random vector $Z$, 就如上面推導, 拆開看各個維度就沒錯了.