搞懂 Quantization Aware Training 中的 Fake Quantization

發表於 | 分類於 | [object Object]

看完本文會知道什麼是 fake quantization 以及跟 QAT (Quantization Aware Training) 的關聯
同時了解 pytorch 的 torch.ao.quantization.fake_quantize.FakeQuantize 這個 class 做了什麼

Fake quantization 是什麼?

我們知道給定 zero ($z$) and scale ($s$) 情況下, float 數值 $r$ 和 integer 數值 $q$ 的關係如下:

$$\begin{align} r=s(q-z) \\ q=\text{round_to_int}(r/s)+z \end{align}$$ 其中 $s$ 為 scale value 也是 float, 而 $z$ 為 zero point 也是 integer, 例如 int8
Fake quantization 主要概念就是用 256 個 float 點 (e.g. 用 int8) 來表示所有 float values, 因此一個 float value 就使用256點中最近的一點 float 來替換
則原來的 floating training 流程都不用變, 同時也能模擬因為 quantization 造成的精度損失, 這種訓練方式稱做 Quantization Aware Training (QAT) (See Quantization 的那些事)

令一個 tensor x 如下, 數值參考 pytorch 官方範例 (link):

1
2
3
4
import torch
import numpy as np
x = torch.tensor([ 0.0552,  0.9730,  0.3973, -1.0780]).requires_grad_(True)

同時令 zero and scale 和 integer 為 int8

1
2
scale, zero = 0.1, 0
quant_min, quant_max = 0, 255

則我們可以使用 torch.fake_quantize_per_tensor_affine (link) 來找出哪一個256點的 float 最接近原來的 x 的 float 值

1
2
3
4
fq_x = torch.fake_quantize_per_tensor_affine(x, scale, zero, quant_min, quant_max)
print(f'fake quant of x = {fq_x} by funtion `fake_quantize_per_tensor_affine`')
# fake quant of x = tensor([0.1000, 1.0000, 0.4000, 0.0000],
#      grad_fn=<FakeQuantizePerTensorAffineCachemaskBackward0>) by funtion `fake_quantize_per_tensor_affine`

其實我們也可以用式 (2) 先算出 quantized 的值, 然後再用 (1) 回算最靠近的 float, 這樣計算應該要跟上面使用 torch.fake_quantize_per_tensor_affine 的結果一樣:

1
2
3
4
5
6
7
8
# We manually check fake quantization results
x_copy = x.clone().detach().numpy()
x_int = np.clip(np.floor(x_copy/scale + 0.5) + zero, quant_min, quant_max)
print(f'quantize x to int = {x_int}')
# quantize x to int = [1.0, 10.0, 4.0, 0.0]
x_back_to_float = (x_int - zero) * scale
print(f'fake quant of x = {x_back_to_float} by manual calculation')
# fake quant of x = [0.1, 1.0, 0.4, 0.0] by manual calculation

Fake quantization 必須要能微分

既然要做 QAT, 也就是說在 back propagation 時, fake quantization 這個 function 也要能微分
我們看一下 fake quantization function 長相: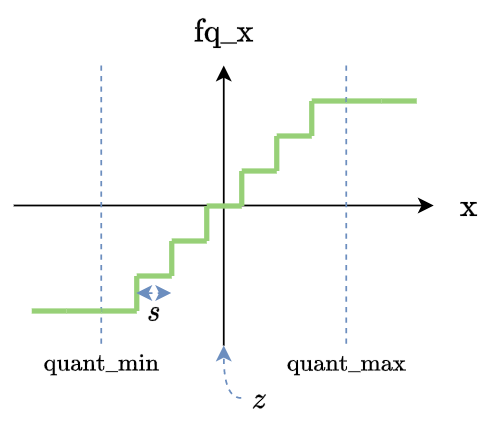

基本上就是一個 step function, 除了在有限的不連續點外, 其餘全部都是平的, 所以 gradient 都是 $0$.
這導致沒法做 back propagation. 為了讓 gradient 流回去, 我們使用 identity mapping (假裝沒有 fake quantization) 的 gradient:

那讀者可能會問, 這樣 gradient 不就跟沒有 fake quantization 一樣了嗎? 如何模擬 quantization 造成的精度損失?
我們來看看加上 loss 後的情形, 就可以解答這個問題
隨便假設一個 loss function 如下(可以是非常複雜的函數, 例如裡面含有NN):
$$\begin{align} loss=(x-0.1)^2 \end{align}$$

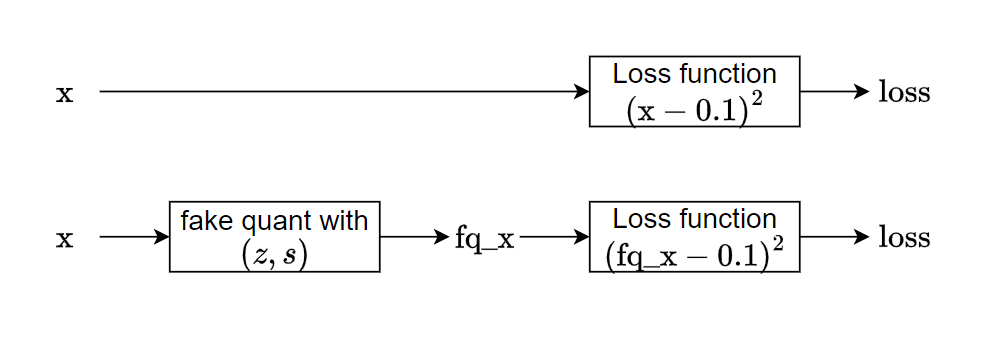
原來的 training flow 是上圖中的上面子圖, loss function 使用 $x$ 代入計算, 而使用 fake quantization training 的話必須代入 $\text{fq_x}$. 這樣就能在計算 loss 的時候模擬精度損失.
我們觀察一下 gradient:
$$\begin{align} \frac{d\text{loss}}{dx}=\frac{d\text{loss}}{d\text{fq_x}}\cdot\frac{d\text{fq_x}}{d\text{x}}= 2(\text{fq_x}-0.1)\cdot \{0\quad\text{or}\quad1\} \end{align}$$ 因此精度損失反應在 $\frac{d\text{loss}}{d\text{fq_x}}$ 這一項上
接續上面的 codes 我們來驗算一下 gradient 是不是如同 (4) 這樣

1
2
3
4
5
6
7
# Note that x = [0.0552,  0.9730,  0.3973, -1.0780]
# and fq_x = [0.1000, 1.0000, 0.4000, 0.0000]
loss = torch.sum((fq_x-0.1)**2)
# loss = tensor(0.9100)
loss.backward()
print(f'gradient of x = {x.grad}')
# tensor([0.0000, 1.8000, 0.6000, -0.0000])

注意到 x.grad[-1] 的值是 $0$, 這是因為 x[-1] 已經小於 quant_min 了, 所以 fake quantization 的 gradient, $\frac{d\text{fq_x}}{d\text{x}}=0$, 其他情況都是 $2(\text{fq_x}-0.1)$.

這個做法跟 so called STE (Straight-Through Estimator) 是一樣的意思 [1], 用來訓練 binary NN [6]
一篇易懂的文章 “Intuitive Explanation of Straight-Through Estimators with PyTorch Implementation“

加入 observer

要做 fake quantization 必須給定 zero and scale $(z,s)$, 而這個值又必須從 input (或說 activation) 的值域分布來統計
因此我們通常會安插一個 observer 來做這件事情
pytorch 提供了不同種類的統計方式來計算 $(z,s)$, 例如:

  • MinMaxObserver and MovingAverageMinMaxObserver
  • PerChannelMinMaxObserver and MovingAveragePerChannelMinMaxObserver
  • HistogramObserver
  • FixedQParamsObserver

因此一個完整個 fake quantization 包含了 observer 以及做 fake quantization 的 function, FakeQuantize 這個 pytorch class 就是這個功能:

observer 只是用來給 $(z,s)$ 不需要做 back propagation
但其實 scale $s$ 也可以 learnable! 參考 “Learned Step Size Quantization“ (待讀)

因此我們可以看到要 create FakeQuantize 時, 它的 init 有包含給一個 observer:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class FakeQuantize(FakeQuantizeBase):
    def __init__(self, observer=MovingAverageMinMaxObserver, quant_min=None, quant_max=None, **observer_kwargs):
        ...
    def calculate_qparams(self):
        #  使用 observer 來計算 zero and scale
        ...
    def forward(self, X):
        if self.observer_enabled[0] == 1:
            # 呼叫 `calculate_qparams` 計算 zeros and scale
            ...
        if self.fake_quant_enabled[0] == 1:
            # 使用 `torch.fake_quantize_per_channel_affine` 來做 fake quantization
            ...
        return X

FakeQuantize 這個 class 是 nn.Module, 只要 forward 裡面的每個 operation 都有定義 backward (都可微分), 就自動可以做 back propagation

本文最開頭有展示 torch.fake_quantize_per_tensor_affine 可以做 backward, 是可以微分的 op

最後, 在什麼地方安插 FakeQuantize 會根據不同的 module (e.g. CNN, dethwise CNN, LSTM, GRU, … etc.) 而不同, 同時也必須考量如果有 batch normalization, concate operation, add operation 則會有一些 fusion, requantize 狀況要注意

Figure Backup

fake_quant.drawio

Reference

  1. Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation: STE paper 2013 Yoshua Bengio
  2. Intuitive Explanation of Straight-Through Estimators with PyTorch Implementation: STE 介紹, 包含用 Pytorch 實作
  3. torch.ao.quantization.fake_quantize.FakeQuantize (link)
  4. torch.fake_quantize_per_tensor_affine (link)
  5. Learned Step Size Quantization: scale $s$ 也可以 learnable (待讀)
  6. 二值网络，围绕STE的那些事儿