在上一篇 搞懂 Quantization Aware Training 中的 Fake Quantization 我們討論了 fake quantization 以及 QAT
提到了 observer 負責計算 zero point and scale $(z,s)$, 一般來說只需要透過統計觀測值的 min/max 範圍就能給定, 所以也不需要參與 backward 計算
直觀上我們希望找到的 zero/scale 使得 quantization error 盡量小, 但其實如果能對任務的 loss 優化, 應該才是最佳的
這就必須讓 $(z,s)$ 參與到 backward 的計算, 這種可以計算 gradient 並更新的做法稱為 learnable quantization parameters
本文主要參考這兩篇論文:
1. LSQ: Learned Step Size Quantization
2. LSQ+: Improving low-bit quantization through learnable offsets and better initialization
LSQ 只討論 updating scale, 而 LSQ+ 擴展到 zero point 也能學習, 本文只推導關鍵的 gradients 不說明論文裡的實驗結果
很快定義一下 notations:
- $v$: full precision input value
- $s$: quantizer step size (scale)
- $z$: zero point (offset)
- $Q_P,Q_N$: the number of positive and negative quantization levels
e.g.: for $b$ bits, unsigned $Q_N=0,Q_P=2^b-1$, for signed $Q_N=2^{b-1},Q_P=2^{b-1}-1$
- $\lfloor x \rceil$: round $x$ to nearest integer
將 $v$ quantize 到 $\bar{v}$ (1), 再將 $\bar{v}$ dequantize 回 $\hat{v}$ (2), 而 $v-\hat{v}$ 就是 precision loss
$$\begin{align}
\bar{v}={clip(\lfloor v/s \rceil+z,-Q_N,Q_P)} \\
\hat{v}=(\bar{v}-z)\times s\\
\end{align}$$
學習 Scale
因為在 forward 的時候是 $\hat{v}$ 去參與 Loss $L$ 的計算 (不是 $v$), 所以計算 $s$ 的 gradient 時 Loss $L$ 必須對 $\hat{v}$ 去微分, 因此
$$\begin{align}
\frac{\partial L}{\partial s}=\frac{\partial L}{\partial \hat{v}}\cdot\frac{\partial \hat{v}}{\partial s}
\end{align}$$ 其中 ${\partial L}/{\partial \hat{v}}$ 是做 backprop 時會傳進來的, 所以需要計算 ${\partial \hat{v}}/{\partial s}$
$$\begin{align}
\frac{\partial \hat{v}}{\partial s}=\frac{\partial(\bar{v}-z)s}{\partial s}=s\cdot
{\color{orange}{\frac{\partial \bar{v}}{\partial s}}}
+\bar{v}-z \\
=s\cdot \left\{
\begin{array}{ll}
−vs^{-2} & \text{if }-Q_N<v/s+z<Q_P \\
0 & \text{otherwise}
\end{array}
\right.
+\bar{v} - z
\end{align}$$ 橘色的地方 $\color{orange}{\partial\bar{v}/{\partial s}}$ 必須使用 STE (Straight Through Estimator) (參考上一篇筆記)
將 $\bar{v}$ 用這樣表達:
$$\begin{align}
\bar{v}=
\left\{
\begin{array}{ll}
\lfloor v/s \rceil + z & \text{if }-Q_N<v/s+z<Q_P \\
-Q_N & \text{if }v/s+z \leq -Q_N \\
Q_P & \text{if }Q_P \leq v/s+z
\end{array}
\right.
\end{align}$$ 所以代回去 (5) 得到我們要的 scale 的 gradients:
$$\begin{align}
\frac{\partial \hat{v}}{\partial s}= \left\{
\begin{array}{ll}
−v/s+\lfloor v/s \rceil & \text{if }-Q_N<v/s+z<Q_P \\
-Q_N - z & \text{if }v/s+z\leq -Q_N \\
Q_P - z & \text{if }v/s+z\geq Q_P
\end{array}
\right.
\end{align}$$ 在 LSQ 這篇的作者把 gradients $\partial\hat{v}/\partial s$ 畫出來, 可以看到在 quantization 的 transition 處, LSQ 能體現出 gradient 變動很大 (另外兩個方法沒有)
Scale 的 Gradient 要做調整
LSQ 作者實驗認為 weights 和 scale 的 gradients 大小, 再除以各自的參數數量後, 如果在比例上一樣的話效果比較好:
$R=\left.\left|\frac{\nabla_s L}{s}\right|\right/\frac{\|\nabla_w L\|}{\|w\|}\approx 1$ 要讓更新的相對大小是接近的, 因此會把 gradients 乘上如下的 scale 值: $g=1/\sqrt{NQ_P}$, 其中 $N$ 是那一層的 (pytorch) tensor 總數量 .numel
Weight tensor $W$ 就是
W.numel, 而如果要處理 scale $s$ 的話, 假設處理的是 activations $X$, 那就是X.numel
實作
這個 gradient scale 的技巧很好, 可以用在任何不想改變 output 大小, 而又希望改變 gradient 大小的場合使用
學習 Zero Point
推導 zero point 的 gradient (式子打不出來很怪, 只能用圖片):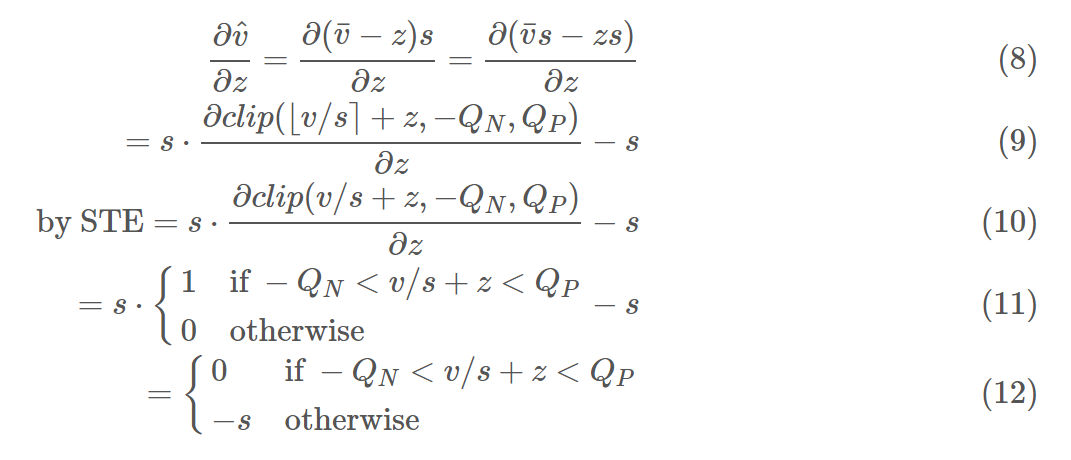
對照 PyTorch 實作
Pytorch 實作: _fake_quantize_learnable_per_tensor_affine_backward 裡面註解寫著如下的敘述:
The gradients for scale and zero point are calculated as below:
Let $X_{fq}$ be the fake quantized version of $X$.
Let $X_q$ be the quantized version of $X$ (clamped at $q_\text{min}$ and $q_\text{max}$).
Let $\Delta$ and $z$ be the scale and the zero point.
式子打不出來很怪, 只能用圖片:
可以發現與 gradient of scale (7) 和 gradient of zero point (12) 能對照起來
一些訓練說明
有關 initialization 可以從 post quantization 開始, 不一定要照論文的方式
其中第一和最後一層都使用 8-bits (我覺得甚至用 32-bits 都可以), 這兩層用高精度能使得效果顯著提升, 已經是個標準做法了
另一個標準做法是 intial 都從 full precision 開始
Reference
- LSQ: Learned Step Size Quantization
- LSQ+: Improving low-bit quantization through learnable offsets and better initialization
- 重训练量化·可微量化参数: 有 zero point 的微分推導
- Pytorch 實作: _fake_quantize_learnable_per_tensor_affine_backward
- 量化训练之可微量化参数—LSQ
- 別人的實作: lsq-net: https://github.com/zhutmost/lsq-net/blob/master/quan/quantizer/lsq.py