我在閱讀這篇論文: “Optimal Clipping and Magnitude-aware Differentiation for Improved Quantization-aware Training” [arxiv] 的時候, 看到這個式子說明 uniform constrained quantizer 有這樣的 quantization error:
$$\begin{align}
J=s_{\text max}^2{4^{-B}\over 3}
\end{align}$$ 當下看得我一頭霧水, 後來查了資料才了解這個 quantization error 的推導, 因此筆記一下. [來源1], [來源2]
這裡要特別說明一下, 這邊的 quantization error 沒有考慮超過最大最小值造成的 clipping error. 將 clipping error 一起考慮是開頭說的那篇論文會探討的情況.
這樣的 quantization error 分析在傳統訊號處理可以看到, 例如 analog 訊號經過 ADC 變成 digital 訊號後會有 quantization 損失. 如果 quantization bit 增加 1 bit 則 SNR 增加約 6dB. 又如果採用 nonlinear quantization 則對音量較低的情況其 SNR 提昇會比 linear quantization 好. Nonlinear quantization 又分 $\mu$-law (北美 and 日本) 和 A-law (歐洲 and 其他). 這些內容在下面的筆記都會解釋. Let’s go~
Uniform Quantization
令 quantization step size 為 $\Delta v=s_{\text max}/2^{B-1}$, 其中 $B$ 為 bit 數, 數值範圍在 $[-s_{\text max},s_{\text max}]$ 之間. 則 input $x$ 和 quantized $x_q$ 的關係如下圖 (圖片裡的 $m_p=s_{max}$): [來源1]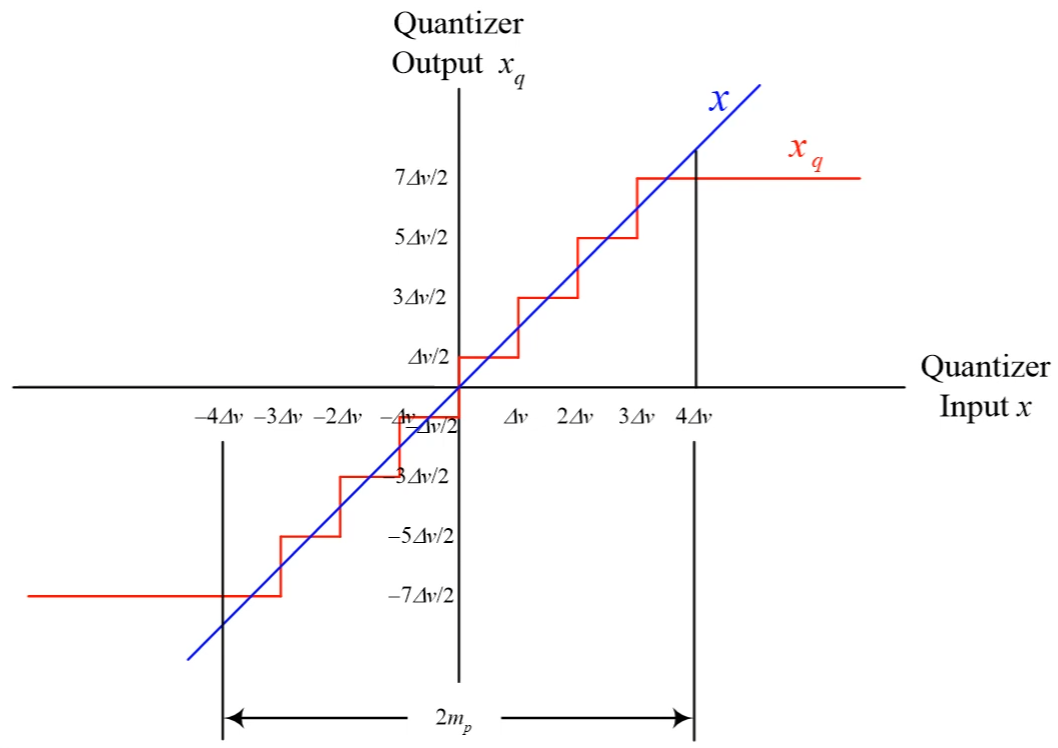
我們將 quantization error $q=x-x_q$ 畫出來則如下圖: [來源1]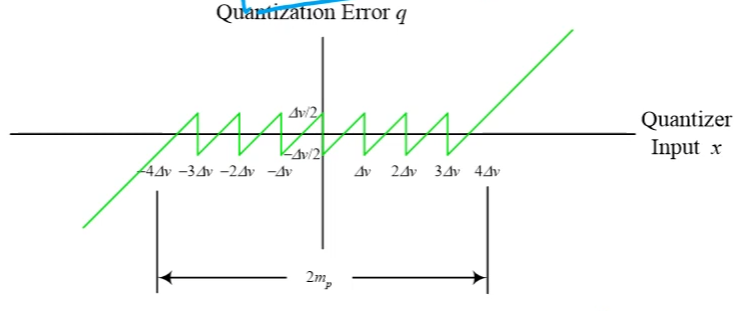
所以 quantization error $q:=x-x_q$ 數值範圍分布在 $[-\Delta v/2, \Delta v/2]$ 之間. 到這邊應該都滿清楚的.
此時做了一個假設, 假設 $q$ 的分布是 uniform distribution, 所以 power of $q$ 的期望值為:
$$\begin{align}
P_q=\int_{-{\Delta v}/2}^{\Delta v/2} q^2{1\over \Delta v}dq \\
= {1\over\Delta v}\left[{q^3\over3}\right]_{-{\Delta v}/2}^{\Delta v /2}=...= {\color{orange}{(\Delta v)^2\over 12}} \\
= \frac{(s_{\text max}/2^{B-1})^2}{12} = s_{\text max}^2\frac{1}{12\cdot2^{2(B-1)}} = {\color{orange}{s_{\text max}^2\frac{4^{-B}}{3}}}
\end{align}$$ 開頭那個奇怪的式子就是這麼來的. 另外 SNR 可以這麼表示:
$$\begin{align}
\text{SNR}=\frac{\text{Signal Power}}{\text{Noise Power}} = \frac{P_s}{P_q}=10\log_{10}\left(\frac{3\cdot4^B}{s_{max}^2}P_s\right) \\
=10\log_{10}\left(3P_s/s_{max}^2\right) + 20B\log_{10}(2) \approx \alpha + 6B
\end{align}$$ 其中 $\alpha$ 與 signal power 有關, 可以發現如果增加 1 bit 的表示能力, SNR 能提升約 6dB.
Non-uniform Quantization
另外考慮到一般訊號數值大的只占少部分, $s_{max}$ 容易被 outlier 影響, 因此 quantization error 就會比較大. 如果說我們先將訊號做 nonlinear 壓縮 (compresser), i.e. 數值大的會被加比較多, 數值小的壓一點就好 (見下圖), 這樣數值間的差異變小後, 再經過 linear quantization 的話, quantization error 就不會那麼大了.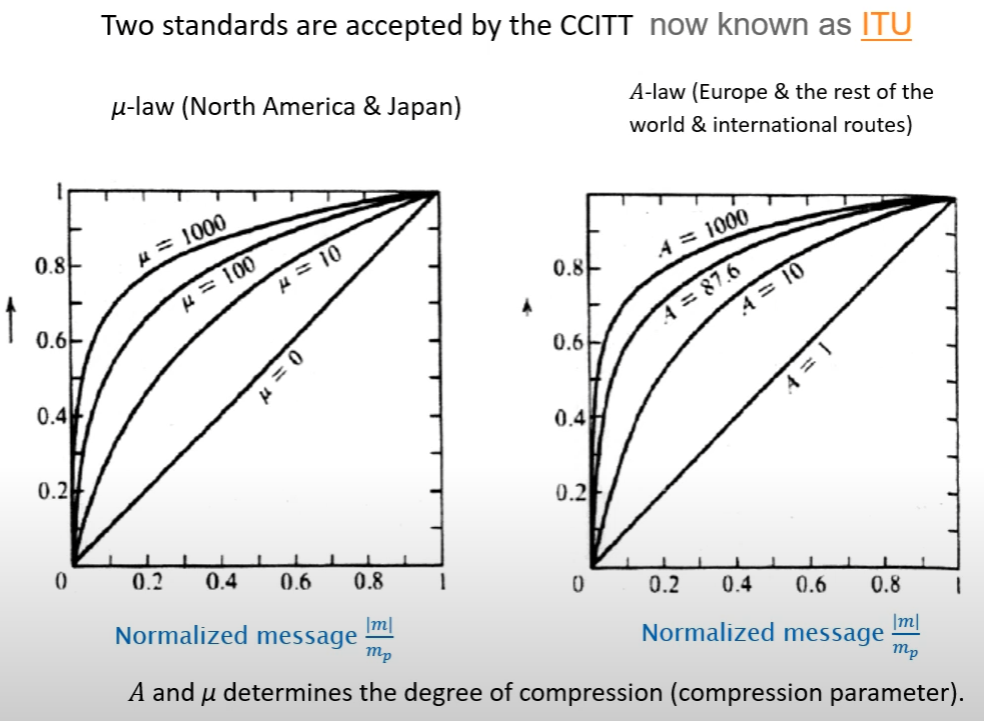
相對的解碼的時候要做擴展 (expander).
由於在 transmitter/receiver 端我們會做 compress/expand, 所以我們稱為 compander = compresser + expander
Telephone system (北美和日本):
- $\mu=100$ for 7-bits (128 levels)
- $\mu=255$ for 8-bits (256 levels)
而在歐洲和其他地方 $A=87.7$ or $87.6$.