Quantization Error (Case with Clipping)

上一篇文章我們提到, uniformly constrained quantizer 有這樣的 quantization error:
$$\begin{align} J=s_{\text max}^2{4^{-B}\over 3} \end{align}$$ 其中 $s_{\text {max}}$ 表示 input $x$ 在 $[-s_{\text {max}}, s_{\text {max}}]$之間.
這麼做雖然能確保所有 $x$ 都不會發生 clipping error, 但如果有一些 outlier 則會使得 quantization step 變很大 (quantization resolution 變低), 因此 quantization 的離散化誤差 (discretization error) 變大.

Quantization error = (Discretization error) + (Clipping error)

舉例來說, 考慮下圖 (ref. from SongHan course EfficientML.ai Lecture 6):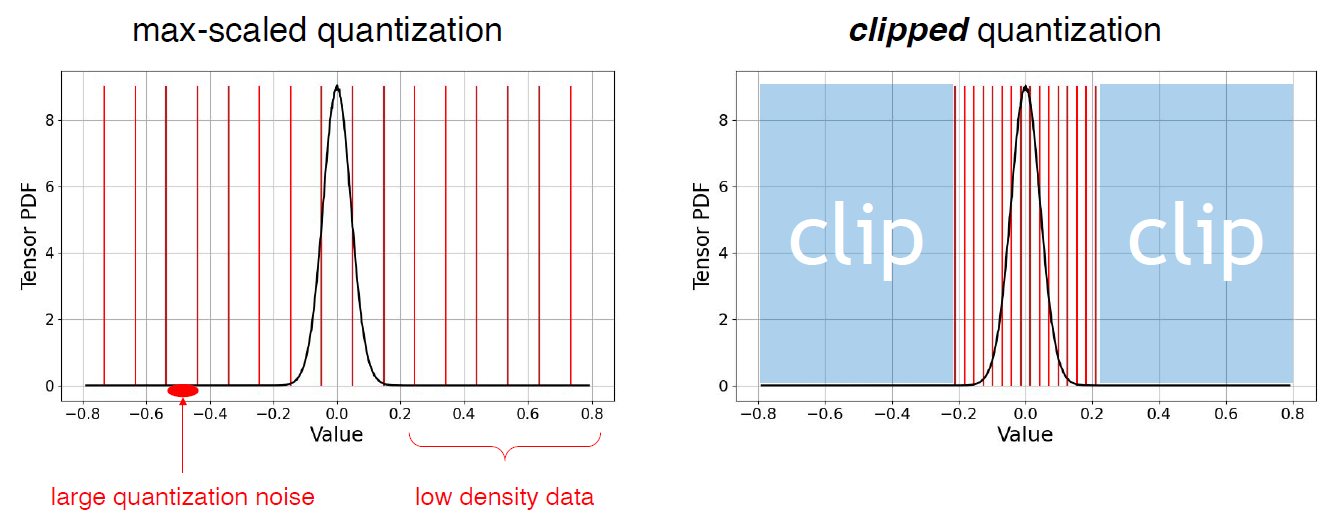

上圖左是 clipping scalar 設定很大, 上圖右則是設定很小. 可以看見 discretization error 跟 clipping error 互為 trade-off.

那麼問題來了, 怎麼設定 clipping scalar, 才會使得整體的 quantization error 最小?
這篇文章 “Optimal Clipping and Magnitude-aware Differentiation for Improved Quantization-aware Training” [arxiv] 給出了理論值, 並使用 Newton’s method 幫助我們很快找到最佳解.

Empirical Quantization Error

Fake quantization 的過程為:
$$\begin{align} \mathcal{Q}(x; s) = \text{clip}\left( s\cdot 2^{1-B}\cdot \text{round}\left(x\cdot 2^{B-1}/s\right), -s, s \right) \end{align}$$ 其中 $B$ 表示我們使用的 quantization bit 數, $s$ 為 clipping scalar. 這裡假設使用 symmetric quantization, i.e. zero point = 0.
因此 empirical 的 error 可以直接計算如下:
$$\begin{align} J_{em}(s)=\mathbb{E}\left[(\mathcal{Q}(X; s)-X)^2\right] \end{align}$$ 我們對 resnet-50 的 layer #17, #45 的 weights 計算 empirical quantization error. (為了驗證論文裡的 Figure 1 (a))
先看一下 layers #17, #45 的 weight 分佈: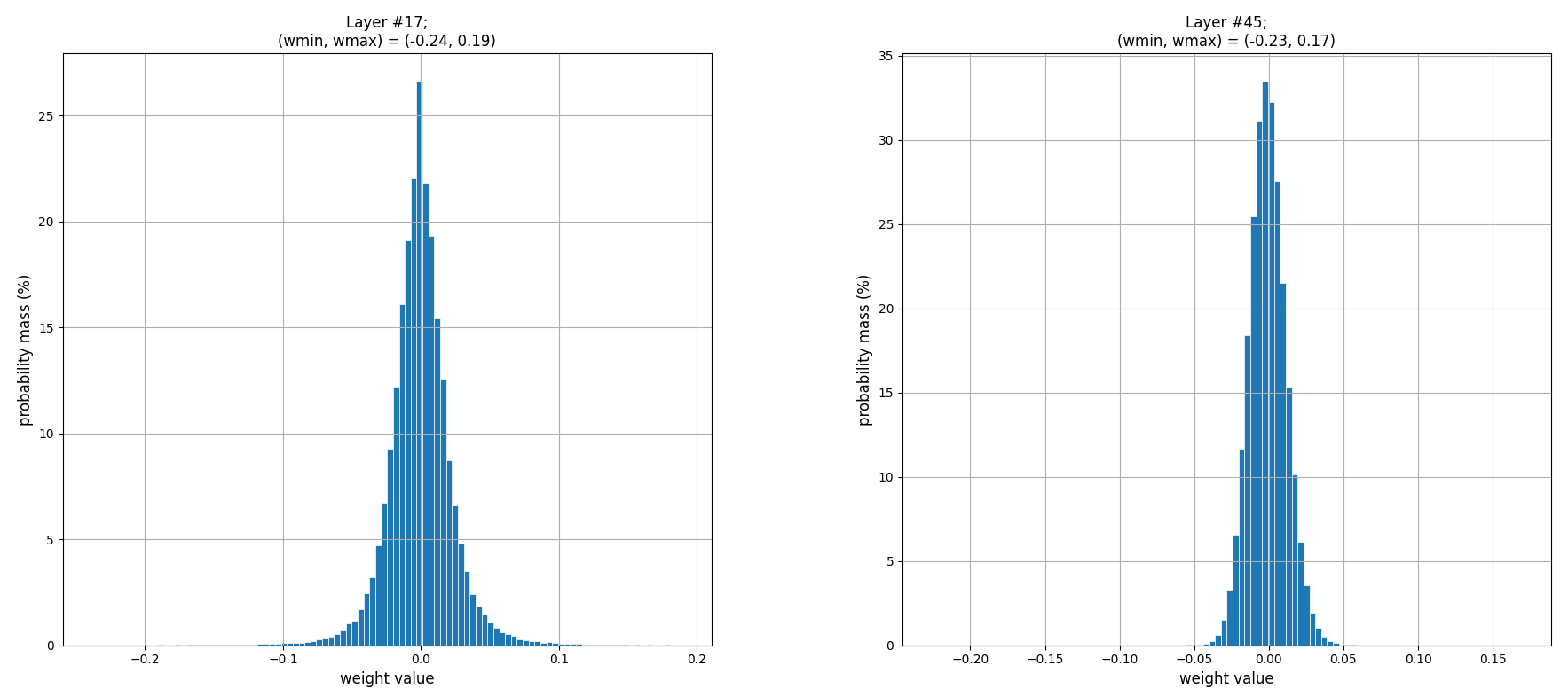

計算 $J_{em}(s)$ 使用 $B=4$-bits 得到如下結果: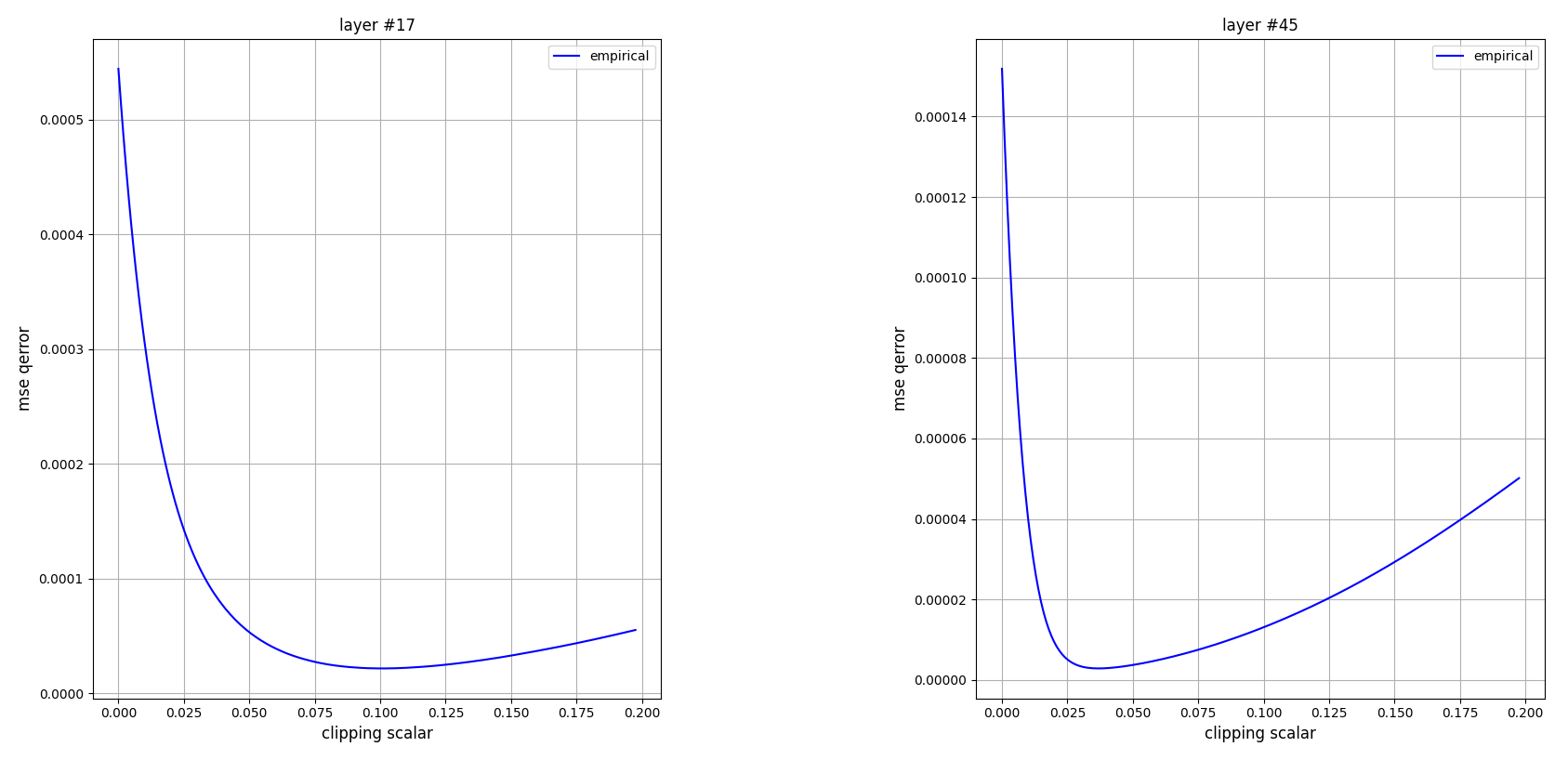

這個 error 曲線看起來很棒啊, 如果是 convex function 則可以很有效率地找到 clipping scalar 的最佳解.
理解一下這個曲線不難發現當 clipping scalar 很小, error 會上升是因為主要來源來自於 clipping error.
但當 clipping scalar 變大, 則 clipping error 會變小但是 discretization error 變大, 因此才會有一個甜蜜點是最小值.
計算 empirical error 主要函式如下:

def cal_qerror(w, qstepsize, zero, bit_num):
    quant_min, quant_max = -(2 ** (bit_num - 1)), 2 ** (bit_num - 1) - 1
    w_q = torch.fake_quantize_per_tensor_affine(torch.as_tensor(w), qstepsize, zero, quant_min, quant_max).numpy()
    return w - w_q
def do_empirical_qerror_scanning(w, qstepsize, zero, bit_num=4, scalar_num=200, plot_ratio=7.0):
    # `qstepsize` stands for quantization step size
    qerrors = []
    clipping_scalars = np.linspace(1e-2, qstepsize * plot_ratio, scalar_num)
    # for loop for each clipping scalar
    for cs in clipping_scalars:
        qerror = cal_qerror(w, 2 * cs / 2**bit_num, zero, bit_num)
        qerrors.append(np.mean(qerror**2))
    return qerrors, clipping_scalars

Theoretical Quantization Error

Quantization 的 MSE 我們可以拆成兩部分:
$$\begin{align} J_{th}(s)={4^{-B}\over 3}s^2\int_0^s f_{|X|}(x)dx + \int_s^\infty (s-x)^2 f_{|X|}(x)dx \end{align}$$ 其中 $f_{|X|}(\cdot)$ 表示 $|X|$ 的 distribution 分佈.
R.H.S. 的第一、二項分別是 discretization 和 clipping error, 應該算好理解.
只是特別說明一下之前推導的 discretization error 是基於 error $(\mathcal{Q}(x; s)-x)$ 為 uniformly distributed. (請參考上一篇文章). 如果不同的 $f_{|X|}(\cdot)$, 是否對於 “$(\mathcal{Q}(x; s)-x)$為 uniformly distributed” 這個假設就不成立呢?
我認為如果 quantization resolution 夠高 (切得夠密), 則 error 的數值其分佈應該會接近 uniformly distributed.

論文裡有這麼一段話: For discretization noise, the term ${s^24^{-B}}/3$ does not require a priori knowledge of data distribution. It is obtained through sampling theory where quantization noise arises via approximating the neighborhood of a quantization level of any distribution as a local rectangle (Widrow & Kollar´ , 2008, book: Quantization noise)

Anyway, 我們可以對上式改寫如下:
$$\begin{align} J_{th}(s)= {4^{-B}\over3}s^2\mathbb{E}\left[\mathbf{1}_{\{|X|\leq s\}}\right] + \mathbb{E}\left[(s-|X|)^2\mathbf{1}_{\{|X|>s\}}\right] \\ = J_1(s) + J_2(s)\\ \end{align}$$ 其中 $\mathbf{1}$ 是 indicator function, 注意到 $\mathbf{1}_{\{|X|\leq s\}}$ 的變數是 $s$, 對於固定的 $X$, $\mathbf{1}_{\{|X|\leq s\}}$ 是個 step function, 只有當 $s\geq|X|$ 的時候 function 值才會是 $1$, 其他情況是 $0$. 此 step function 的微分為 0 almost everwhere. (數學語言是 “微分不為 0 的集合, 該集合的測度為 $0$”)
我們使用 np.histogram 來畫出 theoretical quantization error, 來跟 empirical 比較: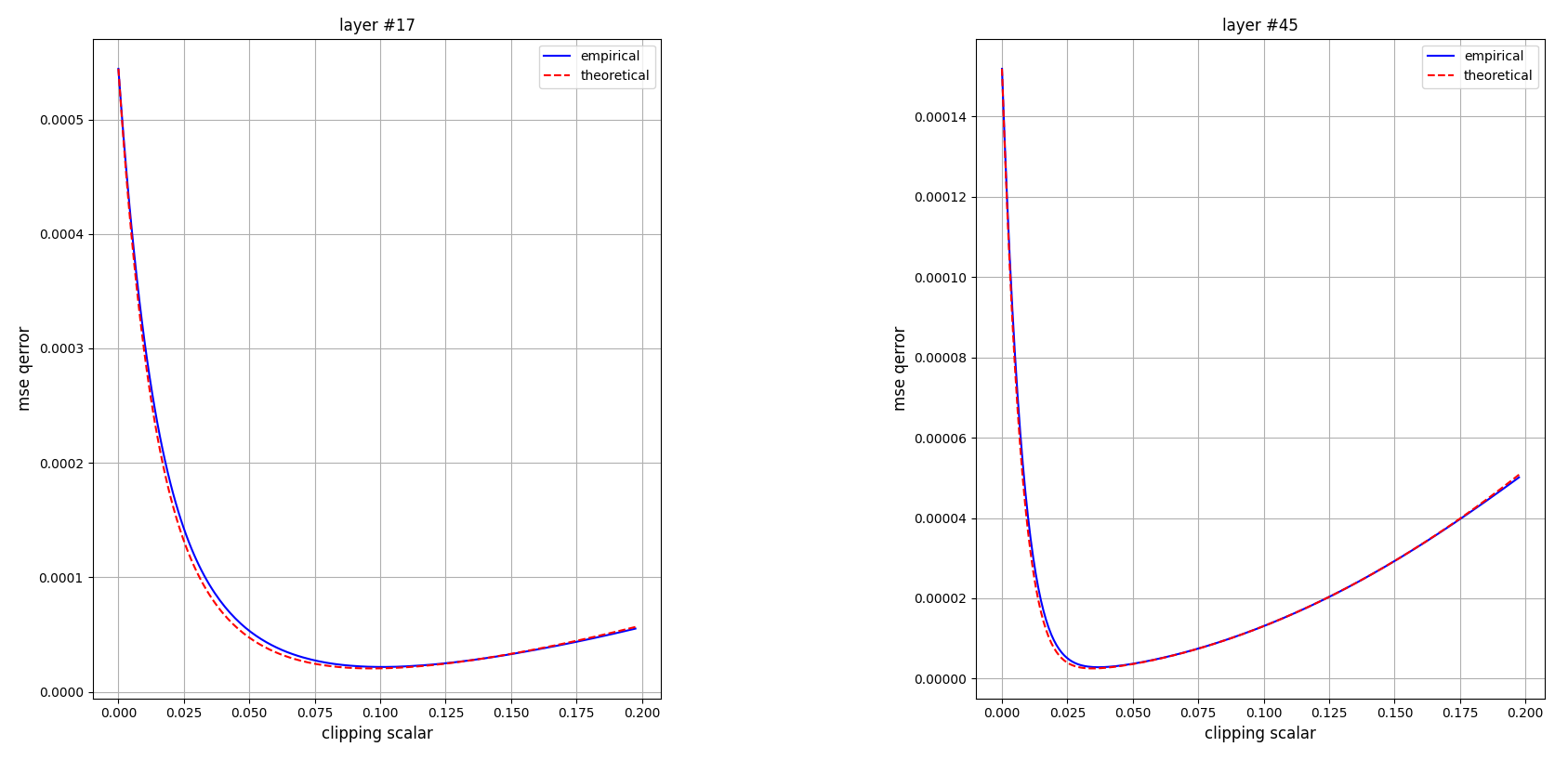

可以發現 theoretical and empirical error curves 很接近! 👏 數學真漂亮!
計算 theoretical error 主要函式如下:

def theoretical_mse_qerror(w, clipping_scalar, bit_num, bins=500):
    hist, bin_edges = np.histogram(np.abs(w), bins=bins, density=False)
    hist = hist / np.sum(hist)  # turn into probability mass (note that it is different with density)
    clip_start_idx = np.where(np.diff(bin_edges > clipping_scalar))[0]
    clip_start_idx = 0 if len(clip_start_idx) == 0 else clip_start_idx[0]
    J1 = np.sum(hist[:clip_start_idx]) * (clipping_scalar**2 / (3 * 4**bit_num))
    J2 = 0.0
    for idx in range(clip_start_idx, len(hist)):
        prob_x_mass = hist[idx]
        x = (bin_edges[idx + 1] + bin_edges[idx]) / 2
        J2 += (clipping_scalar - x) ** 2 * prob_x_mass
    return J1 + J2

找出最佳 Clipping Scalar

我們計算一下 $J_1$ 的 gradient:
$$\begin{align} J_1'(s)={4^{-B}\over3}\cdot2 s\cdot\mathbb{E}\left[\mathbf{1}_{\{|X|\leq s\}}\right] + {4^{-B}\over3}s^2\frac{\partial}{\partial s}\mathbb{E}\left[\mathbf{1}_{\{|X|\leq s\}}\right] \\ = {4^{-B}\over3}\cdot2 s\cdot\mathbb{E}\left[\mathbf{1}_{\{|X|\leq s\}}\right] + {4^{-B}\over3}s^2\mathbb{E}\left[\frac{\partial}{\partial s}\mathbf{1}_{\{|X|\leq s\}}\right] \\ ={4^{-B}\over3}\cdot2 s\cdot\mathbb{E}\left[\mathbf{1}_{\{|X|\leq s\}}\right] + 0 \end{align}$$ (7) 到 (8) 是因為 expectation 的變數為 $X$ 跟 $s$ 無關, 所以微分跟 expectation 可以互換.
(9) 是因為之前說過, 因為 $\mathbf{1}_{\{|X|\leq s\}}$ 是 step function, 所以其 gradient 為 $0$ almost everwhere.
同理 $J_2$ 的 gradient:
$$\begin{align} J_2'(s) = \frac{\partial}{\partial s}\mathbb{E}\left[ (s-|X|)^2\mathbf{1}_{\{|X|>s\}} \right] = \mathbb{E}\left[ \frac{\partial}{\partial s} \left( (s-|X|)^2\mathbf{1}_{\{|X|>s\}} \right) \right] \\ =\mathbb{E}\left[ 2(s-|X|)\mathbf{1}_{\{|X|>s\}} + (s-|X|)^2\frac{\partial}{\partial s}\mathbf{1}_{\{|X|>s\}} \right] \\ = \mathbb{E}\left[ 2(s-|X|)\mathbf{1}_{\{|X|>s\}} + 0 \right] \end{align}$$ (12) 是因為之前說過, 因為 $\mathbf{1}_{\{|X|> s\}}$ 是 step function, 所以其 gradient 為 $0$ almost everwhere.
所以 $J_{th}$ 的 gradient:
$$\begin{align} J_{th}'(s)= {4^{-B}\over3}\cdot2 s\cdot\mathbb{E}\left[\mathbf{1}_{\{|X|\leq s\}}\right] + \mathbb{E}\left[ 2(s-|X|)\mathbf{1}_{\{|X|>s\}} \right] \end{align}$$ 同樣的推導 $J_{th}''$ 為:
$$\begin{align} J_{th}''(s) = {4^{-B}\over3}\cdot2 \cdot\mathbb{E}\left[\mathbf{1}_{\{|X|\leq s\}}\right] + 2\mathbb{E}\left[\mathbf{1}_{\{|X|>s\}}\right] \end{align}$$

因此根據 Newton’s method, $s_{n+1}=s_n-J_{th}'(s)/J_{th}''(s)$, 得到:
$$\begin{align} s_{n+1}=\frac{\mathbb{E}\left[|X|\cdot\mathbf{1}_{\{|X|>s_n\}}\right]} { {4^{-B}\over3}\mathbb{E}\left[\mathbf{1}_{\{|X|\leq s_n\}}\right] + \mathbb{E}\left[\mathbf{1}_{\{|X|>s_n\}}\right] } \end{align}$$

實務上 Newton’s method 很 robust, initial $s_1$ 選擇 $\{0,s_{max},3\sigma,4\sigma,5\sigma\}$ 都可以有效收斂. 論文裡直接選擇 $s_1=({\sum_x|x|})/(\sum_x\mathbf{1}_{|x|>0})$, 相當於 $s_1=s_{max}$ iterates 到 $s_3$ 的情況.

我們實際用 Newton’s method 設定 s_init=0.0 和 10 次 iteration 的結果如下: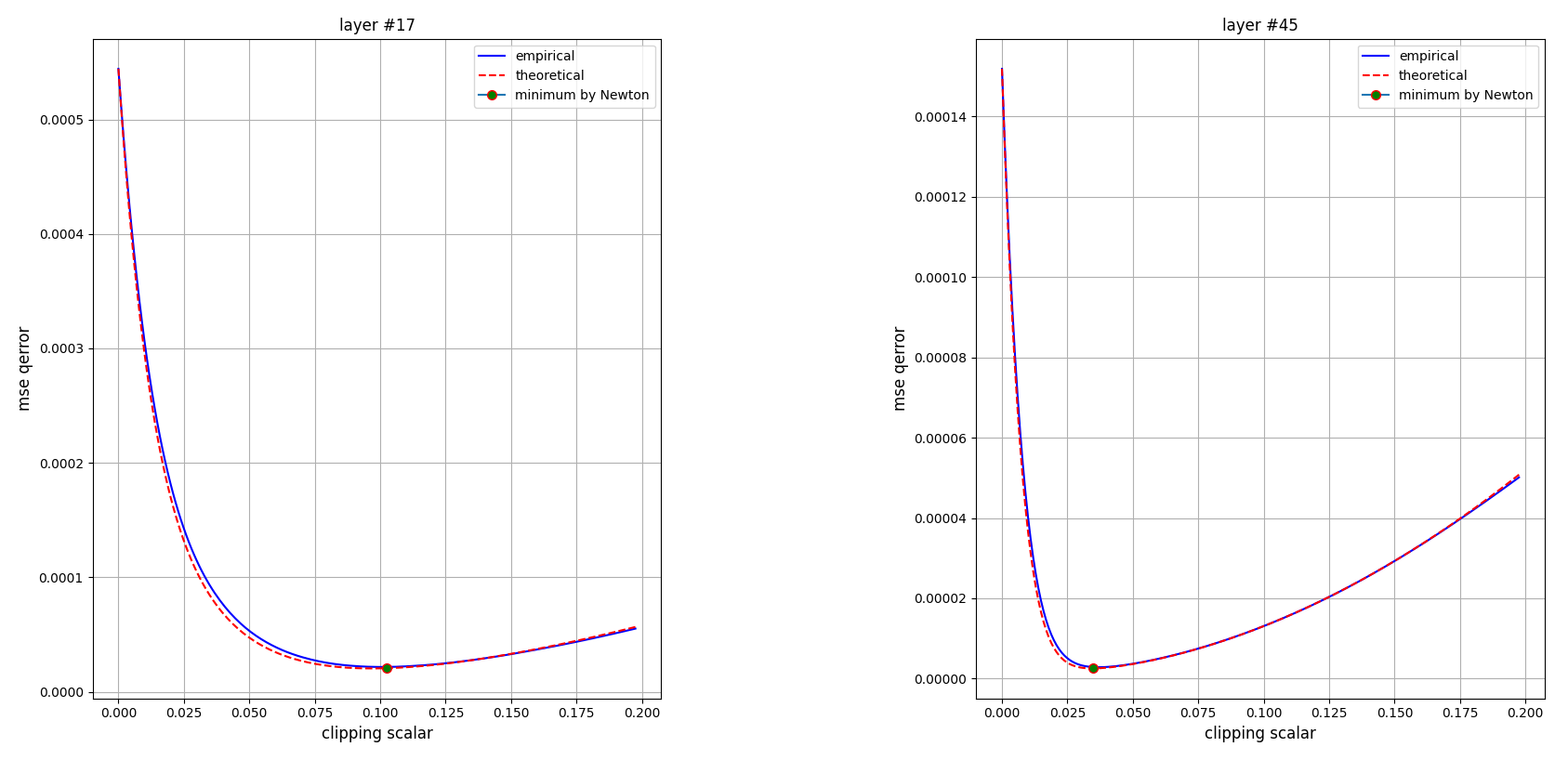

確實能找出最佳的 clipping scalar. 到這裡算是複現了論文裡的 Figure 1 (a) 了.
計算 optimal clipping scalar 主要函式如下:

def find_opt_by_Newton_method(weights, bit_num, cs_init=0.0, iter_num=10):
    # `cs` stands for `clipping scalar`
    weights_abs = np.abs(weights)
    cs_cur = cs_init
    for itr in range(iter_num):
        indicator_larger = weights_abs > cs_cur
        indicator_smaller = weights_abs <= cs_cur  # should we ignore case with `==0`?
        numerator = np.sum(weights_abs[indicator_larger])
        denominator = np.sum(indicator_smaller) / (3 * 4**bit_num) + np.sum(indicator_larger)
        cs_cur = numerator / denominator
    return cs_cur

Short Summary

常用的 uniform quantization 包含兩個參數 scale and zero_point, 一般可以使用 observer 來統計出數值分佈的最大最小值進而得到 clipping scalar (通常會搭配 moving averaging 來減緩 outlier 的影響).
但這樣得到的 quantization error 沒有辦法保證是最小的.
本文介紹的這篇論文把 quantization error 的理論值找出來, 並使用 Newton’s method 非常有效率的找出最佳 clipping scalar. 甚至可以鑲嵌在 QAT iteration 中.
另一方面, 這篇論文找的最佳解跟任務的 loss function $\mathcal{L}$ 無關. 如果希望跟 loss function 有關, 可以考慮使用 LSQ+ 或 PACT 的方式來學習出 scale and zero_point.
總之這篇論文讓我們對 uniform quantization 的 error 有了更深入的理解, 也很漂亮得提供了高效求解方法.

References

Optimal Clipping and Magnitude-aware Differentiation for Improved Quantization-aware Training, [arxiv]
SongHan course EfficientML.ai Lecture 6
複現論文 Figure 1 (a) 的 [Github]
Learning Zero Point and Scale in Quantization Parameters [link]