總歸來說 Data-Free Quantization (DFQ) 的目的是讓 floating model 做 weights 各種調整, 使得不管是 weights or activations 都變得適合 per tensor 量化.這樣理想上就不需用到 per channel 量化, 因為 per channel 雖然效果很好, 但硬體比較不友善, 且花的運算量較高. 另外 DFQ 屬於 Post-Training Quantization (PTQ) 方法. PTQ 對佈署到 edge 端很方便, 但一般來說 PTQ 都不如 Quantization-Aware Training (QAT) 的效果好, 因此 DFQ 嘗試提升效果.
DFQ 共四步, 對照圖看, 需照順序: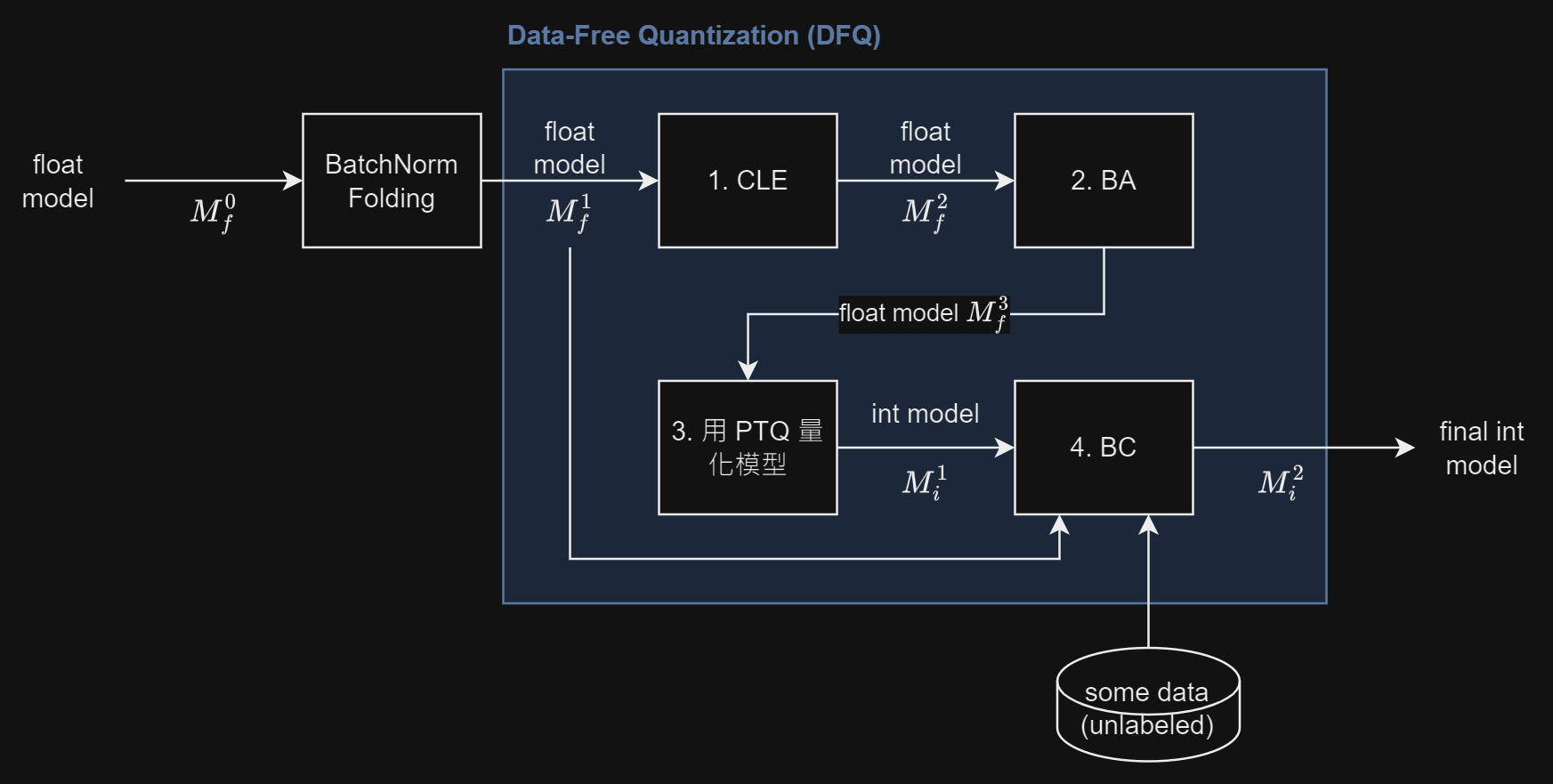
- Cross-Layer Equalization (CLE): 輸入 fused BN 後的 float model $M_f^1$, floating 操作對 weights 做調整使得更均衡方便 per tensor 量化, 為 step 3 的前置作業, 輸出仍為 float model $M_f^2$.
- Bias Absorption (BA): 輸入 CLE 後的 float model $M_f^2$, floating 操作對 activations 做調整使得更均衡方便 per tensor 量化, 為 step 3 的前置作業, 輸出仍為 float model $M_f^3$.
- PTQ 量化: 輸入 CLE+BA 後的 float model $M_f^3$, 此時不管 weights or activations 都適合做 per-tensor 量化了, 所以直接 PTQ 輸出 int model $M_i^1$.
- Bias Correction (BC): 輸入 float model $M_f^1$ 和 step 3 的 $M_i^1$, 並且(option)給一些 unlabeled 的代表 data, BC 會對 $M_i^1$ 的 bias 參數補償因為量化造成的數值 mean 偏移, 輸出為最終 fixed point model $M_i^2$.
Qualcomm AI Lab 的 tool AIMET 說 BC 這一步驟可以用 AdaRound (需要一小部分的 unlabelled training data) 取代
其實認真看完論文, 覺得限制有點多啊! 很多時候不能套 CLE, 有時 BA 也用不了. 把限制條列一下:
⚠️ CLE 限制:
1. Activation functions $f(\cdot)$ 需為 piece-wise linear (e.g. ReLU, ReLU6, LeakyReLU, …)
2. 如果有 BN (Batch normalization) layer, 先把它 fuse 到 Conv 裡面, 所以第3點的限制才可以忽略 BN layer.
3. 相鄰的 layers 只能很單純是 $f(W^{(2)}f(W^{(1)}x+b^{(1)})+b^{(2)})$, 所以如果有 residual add 或 concat 才給 $W^{(2)}$ 作用的話就不行.
⚠️ BA 限制:
1. activations 的每個維度是高斯分佈, 或能取得其分布, 例如透過 observer; 但在 AIMET 工具是假設有 BN 所以是高斯分布, 否則不用套用 BA
2. Activation functions $f(\cdot)$ 需為 ReLU (or ReLU6), LeakyReLU 這種不行
⚠️ BC 限制:
Empirical BC 需要給 representative data (可以是 unlabeled). 如果 Analytical BC (data-free) 則需有 BN —> ReLU —> Conv/FC 這樣順序的假設才能補償因 quantize 後 Conv/FC 這層輸出的 mean 偏移
接著我們描述一下 CLE, BA 和 BC 的動機, 然後再詳細介紹論文提出的這三個方法
Motivation
CLE 動機
Convolution kernels 在不同 output channels 來看, weights 的分佈有些很大有些很小, 這使得用統一一個 quantization parameter set 會不好. 所以如果能事先讓 weights 在不同 channel 的數值分佈接近, 這樣就適合用 per tensor quantization 了. 為此作者提出 Cross-Layer Equalizaiton (CLE) 方法.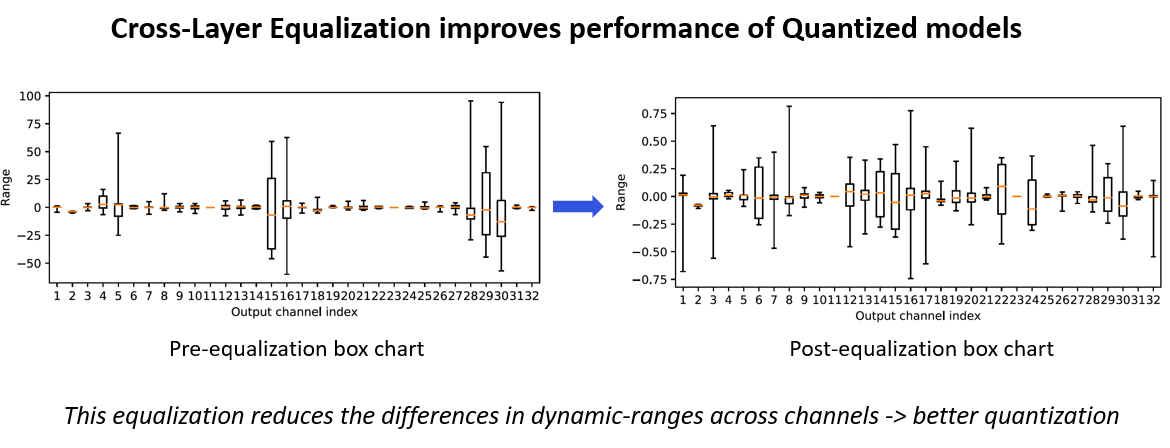
圖來源為 AIMET Post-Training Quantization Techniques
BA 動機
不過做了 CLE 有個 side-effect 就是讓 activations 有可能反而不同 channels 分佈變的更不同, 為此作者提出 Bias Absorption (BA) 方法使得 activations 同樣適合 per-tensor quant.
BC 動機
另一方面, 其實 weights or input activations 經過 quantization 後, output activations 理想上希望是 un-biased, 但實際上都會有 bias, 如下圖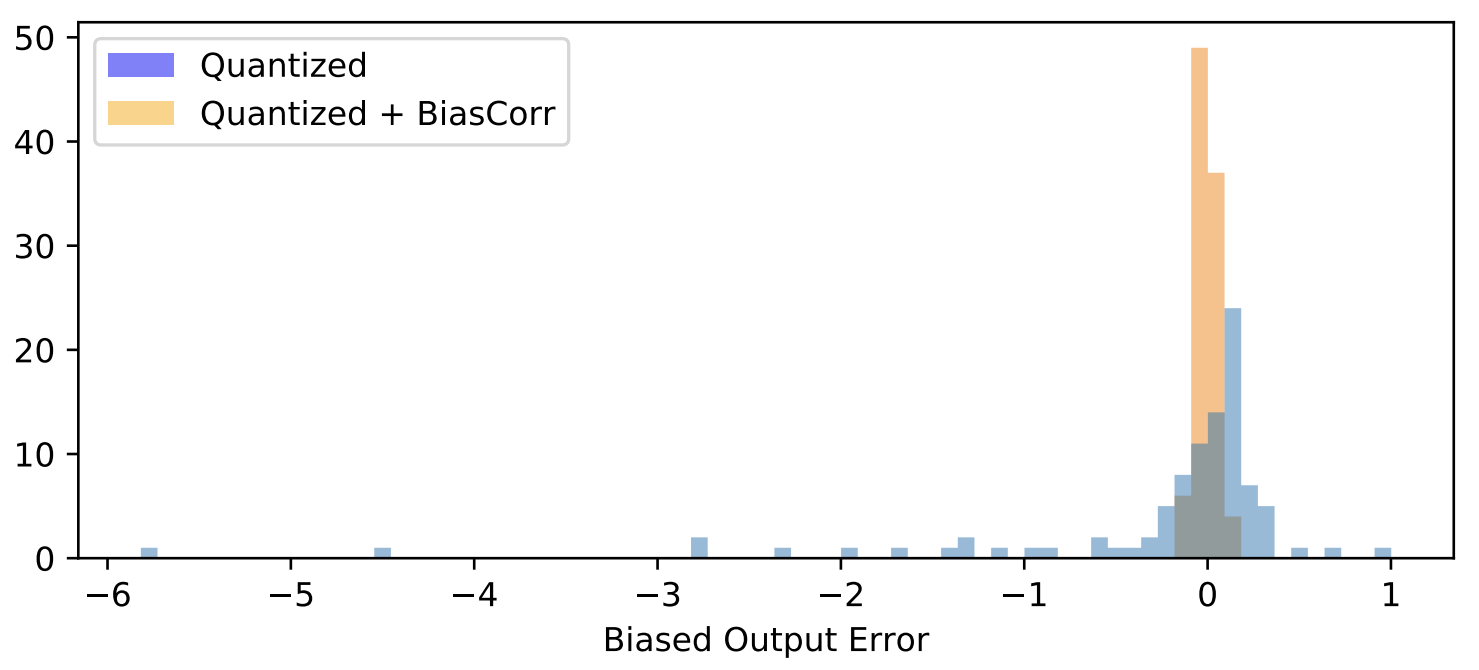
$$\begin{align} \mathbb{E}[\tilde{y}_j-y_j]\approx{1\over N}\sum_n\left(\tilde{W}x_n\right)_j - \left(Wx_n\right)_j \end{align}$$ 其中 $\tilde{W},\tilde{y}$ 分別是 quantized weight and output activation. 所以作者提出使用 Bias Correction (BC) 技巧來彌補.
Data Free Quantization (DFQ) 詳細解釋
Cross-Layer Equalization (CLE), 幫助 weights per-tensor 量化
對任何 $s>0$, 且 $f(\cdot)$ 是 piece-wise linear activation function:
$$\begin{align}
f(x)=\left\{
\begin{array}{rl}
a_1x+b_1 & \text{if }x\leq c_1 \\
a_2x+b_2 & \text{if }c_1<x\leq c_2 \\
\vdots \\
a_nx+b_n & \text{if } c_{n-1}<x \\
\end{array}
\right.
\end{align}$$ 則我們可以找出等價的 $\hat{f}(\cdot)$ 使得 $f(sx)=s\hat{f}(x)$: 設定 $\hat{a}_i=a_i$, $\hat{b}_i=b_i/s$ and $\hat{c}_i=c_i/s$.
這麼做有什麼好處呢? 考慮以下的情形
給定兩個相鄰的 layers: $h=f(W^{(1)}x+b^{(1)})$ 和 $y=f(W^{(2)}h+b^{(2)})$, 其中 $f$ 是 piece-wise linear activation function.
則我們有:
$$\begin{align}
y=f(W^{(2)}f(W^{(1)}x+b^{(1)})+b^{(2)}) \\
=f(W^{(2)}S\hat{f}(S^{-1}W^{(1)}x+S^{-1}b^{(1)})+b^{(2)}) \\
=f(\hat{W}^{(2)}f(\hat{W}^{(1)}x+\hat{b}^{(1)})+b^{(2)})
\end{align}$$ 其中 $S=\text{diag}(s)$ 表示對角矩陣, $S_{ii}$ 是 neuron $i$ 的 scaling factor $s_i$. 就是靠這 $s$ 來調節 weights 分布.
所以我們重新縮放了 weights: $\hat{W}^{(2)}=W^{(2)}S$, $\hat{W}^{(1)}=S^{-1}W^{(1)}$ and $\hat{b}^{(1)}=S^{-1}b^{(1)}$.
那麼怎麼設定最佳的 $S$ 呢? 理想上, 透過 $S$ 我們希望將 $\hat{W}^{(1)}, \hat{W}^{(2)}$ 變成適合 per tensor quantization.
- 定義 $r_i^{(1)}:=\max(W_{i,:}^{(1)})$, 即為 $W^{(1)}$ 的 $i^{th}$ row vector 取 max.
- 同理 $\hat{r}_i^{(1)}:=\max(\hat{W}_{i,:}^{(1)})=r_i^{(1)}/s_i$.
類似地我們定義
- $r_j^{(2)}:=\max(W_{:,j}^{(2)})$, 即為 $W^{(2)}$ 的 $j^{th}$ column vector 取 max.
- $\hat{r}_j^{(2)}:=\max(\hat{W}_{:,j}^{(2)})=s_j\cdot r_j^{(2)}$.
注意到一個是 row vector 另一個是 column vector 這是因為 $W^{(1)}$ 的 row vector 對應的是 $W^{(2)}$ 的 column vector. 即第一層 layer 的 output channel 對應的是第二層 layer 的 input channel 的概念
然後再令整個 weight matrix 的最大值為: $R^{(1)}:=\max_i(r_i^{(1)})$ 和 $R^{(2)}:=\max_j(r_j^{(2)})$
大概示意圖長這樣子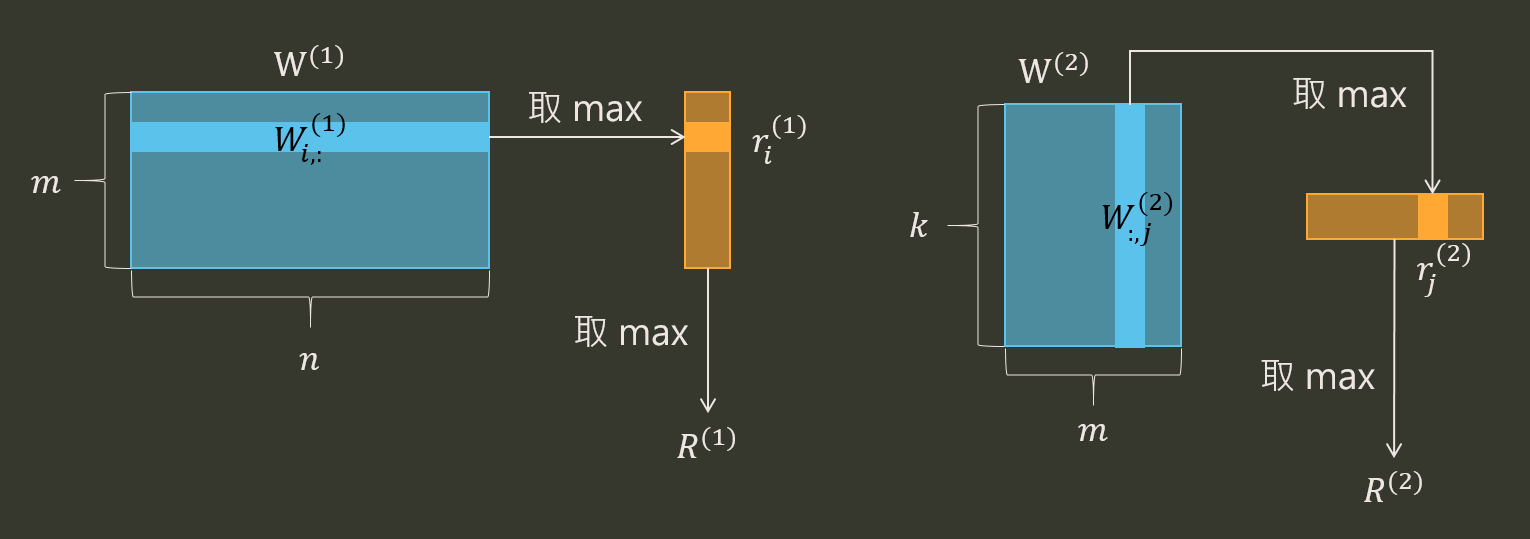
最後就可以定義每一個 channel (1~m) 對於整個 weight matrix 的占比:
$p_i^{(1)}=r_i^{(1)}/R^{(1)}$; $\hat{p}_i^{(1)}=\hat{r}_i^{(1)}/\hat{R}^{(1)}$; 同理 $p_j^{(2)},\hat{p}_j^{(2)}$
到這裡不難理解, 只是很多 terms 要消化一下而已
$p_i^{(1)}$ 表示 $i^{th}$ row vector 對整個 matrix $W^{(1)}$ 的佔比, 想像上如果每個 rows 的佔比都很大, 那就整體適合 per-tensor quantization.
可以想像, 若 $\hat{p}_i^{(1)}$ 比 $p_i^{(1)}$ 大表示 $i^{th}$ row vector 的佔比經過 $s_i$ 的調整變大, 但由於 $s_i$ 在 $W^{(1)}$ 用除的但在 $W^{(2)}$ 用乘的, 導致 $\hat{p}_i^{(2)}$ 比 $p_i^{(2)}$ 小了, 意思是 $i^{th}$ column vector 的佔比反而變小. 所以一邊變大了但反而使另一邊變小了, 這一定是個 trade-off.
所以我們希望兩邊都顧到 ($\hat{p}_i^{(1)} \hat{p}_i^{(2)}$ 一起考慮) , 作者就定義了這樣的目標函式:
$$\begin{align}
\max_S \sum_i \hat{p}_i^{(1)} \hat{p}_i^{(2)}
\end{align}$$ 調整 $S$ 使兩邊 matrix $W^{(1)},W^{(2)}$ 的占比都要顧到, 找出使得總佔比量最大的 $S$.
這個問題的最佳解在論文的 Appendix A 有證明, 我們先把解寫出來:
$$\begin{align}
s_i=\frac{1}{r_i^{(2)}}\sqrt{r_i^{(1)}r_i^{(2)}}
\end{align}$$ 這樣的 $s_i$ 會使得 $\hat{r}_i^{(1)}=\hat{r}_i^{(2)}$, $\forall i$. 把 $s_i$ 代到 $\hat{r}_i^{(1)}$ and $\hat{r}_i^{(2)}$ 就知道了. (這裡原論文寫 $r_i^{(1)}=r_i^{(2)}$ 應該是 typo)
詳細證明記錄在最後的 Appendix (論文證明有些沒懂補充一下自己想法).
Bias Absorption (BA), 幫助 activation per-tensor 量化
再說之前, 先了解以下範例.
首先對於 ReLU $r(\cdot)$ 來說一定存在一個 non-negative vector $c$ 使得 $\forall x$
$$r(Wx+b-c)=r(Wx+b)-c; \quad \forall x \qquad\qquad (\star)$$ $c=0$ 就是一個 trivial 解.
舉一個簡單範例, 考慮某一個 channel $i$, data $Wx_i$ 的機率分佈為直角三角形: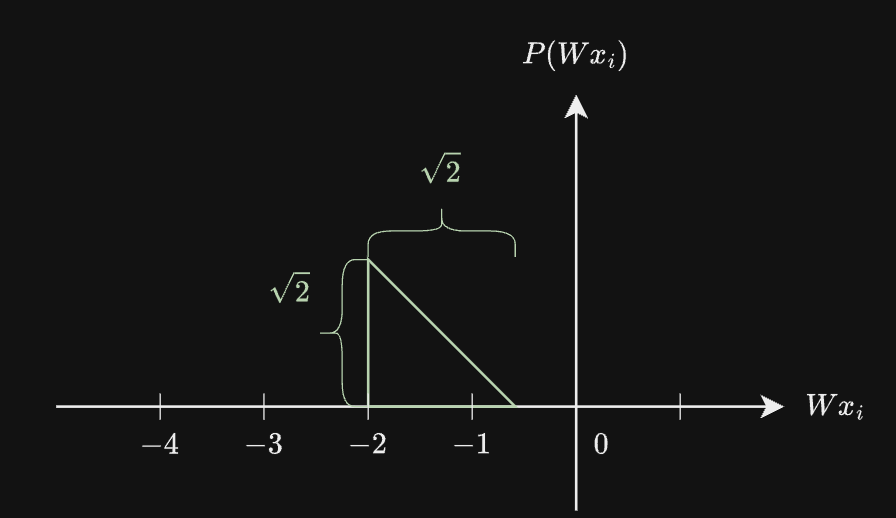
當 $b=3$ 的情況時, 則選 $c=0.5$ 滿足 $(\star)$ 條件, 見下圖:
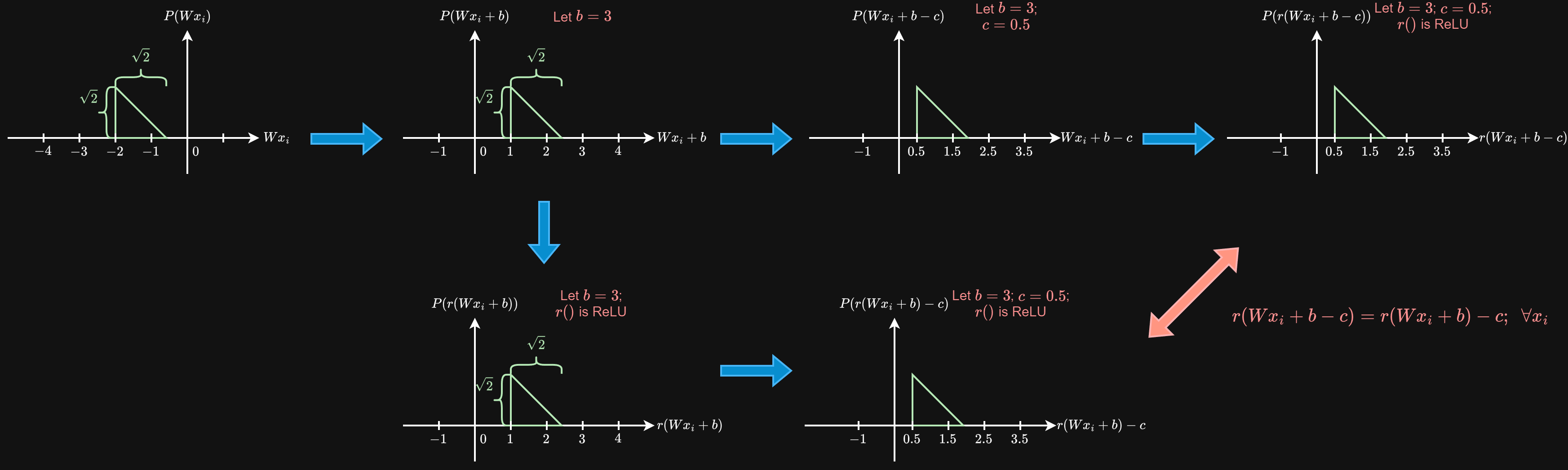這個情況會滿足所有 $x$, 但如果 $Wx$ 的分布不像範例一定大於某一個值 (想像上面的直角三角形分布變成高斯分佈) 則我們只能選擇滿足大部份的值
如果是高斯分佈的話 (則 Batch norm 的 mean, std 就可拿來用), 論文選擇 3 個標準差所以保證 99.865% 滿足. 高斯分佈在 $\mu\pm3\sigma$ 內的機率約為 $0.9973002$ [ref], 但由於我們要找的 $c$ 只會忽略 $<\mu-3\sigma$ 的情況所以是 $1-(1-0.9973002)/2\approx99.865$, 之後會有圖示比較清楚
有了以上概念後, 回頭過來看看經過 CLE 後還會發生什麼現象, 其中 $r(\cdot)$ 是 ReLU.
(突然渲染不出數學式子…煩阿)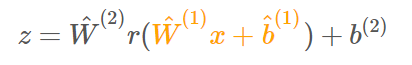
$\hat{W}^{(1)}$ and $\hat{W}^{(2)}$ 已經被 CLE 調整一波後數值分佈變得很接近 (適合 per-tensor quantization 👏🏻)
但 $\hat{b}^{(1)}=S^{-1}b^{(1)}$, 當 $s_i<1$ 的時候會讓 channel $i$ 的 activation 放大導致 activations, $\hat{W}^{(1)}x+\hat{b}^{(1)}$, 的各 channel 之間分佈位置會不同, 因此也會讓 activations 不好做 quantization!
利用上面說的概念我們這樣推導: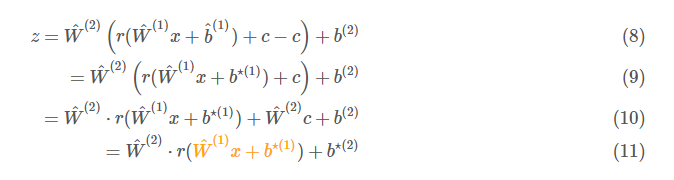
其中 $b^{\star(1)}=\hat{b}^{(1)}-c$ 和 $b^{\star(2)}=\hat{W}^{(2)}c+b^{(2)}$.
💡 目的是把 $\color{orange}{\hat{W}^{(1)}x+\hat{b}^{(1)}}$ 從不適合做 per-tensor quant 變成 $\color{orange}{\hat{W}^{(1)}x+b^{\star(1)}}$ 容易做 per-tensor quant.
則 $c$ 可以選擇盡量滿足所有 $\hat{W}^{(1)}x+\hat{b}^{(1)}$ 的值, 要這麼做最暴力的方式是餵所有 training data 去看資料分布, 選擇滿足大部分的情況, 例如滿足 99.99% 的數值.
另外如果我們知道 $\hat{W}^{(1)}x+\hat{b}^{(1)}$ 會再經過 Batch normalization, i.e. $BN(\hat{W}^{(1)}x+\hat{b}^{(1)})$ 只是 BN 忽略不寫而已, 則令 $c=\max(0,\beta-3\gamma)$, 其中 $\beta,\gamma$ 分別是 Batch normalization 的 shift and scale parameters, 這樣直接就滿足大於-3標準差的 99.865% 機率了.
開頭的 DFQ 流程圖有先做 BN folding, 所以此時的 $\tilde{W}^{(1)}$ 已經是 folding 後的, 因此要事先把 $\beta,\gamma$ 存起來才能在這步驟用
我們來思考為啥 activations 從 $\hat{W}^{(1)}x+\hat{b}^{(1)}$ 變成 $\hat{W}^{(1)}x+b^{\star(1)}$ 後就會比較好做 per-tensor quantization, 這是因為我們選擇的這些 $c_i$ 會讓維度 $i$ 的 activation 對齊到剛好有 99.865% 大於 0, 而每個維度都依這樣的標準 align 自然就容易對整個 activations 做 quantization 了 (不需要 per-channel quant 了)!
圖示一下上面的意思, 為了方便令 $\hat{k}=\hat{W}^{(1)}x+\hat{b}^{(1)}$, 其中 $\hat{k}_i$ 表示第 $i$ 維, 同理 $k^{\star}=\hat{W}^{(1)}x+b^{\star(1)}$ 和 $k^\star_i$: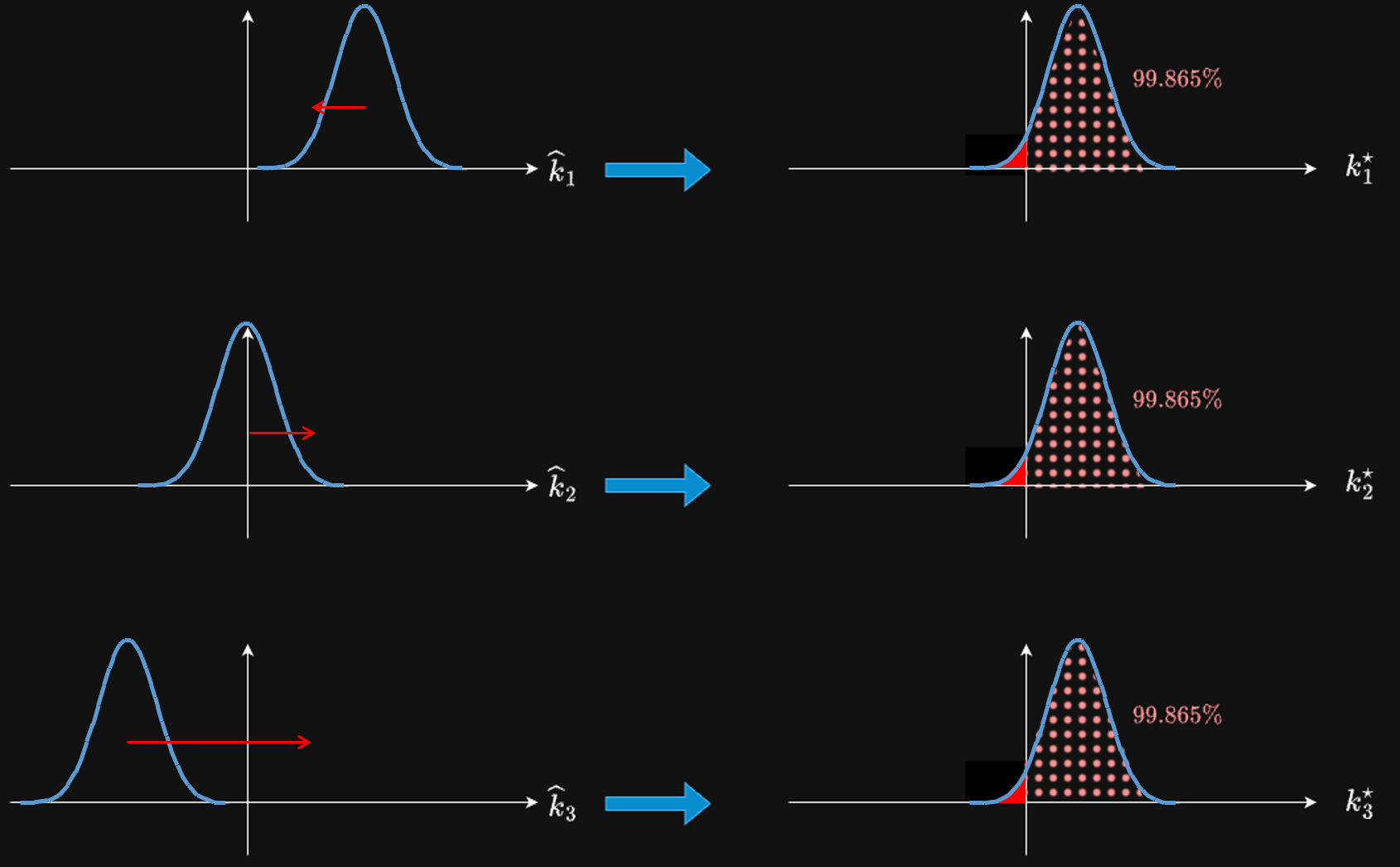
注意到雖然 activations $k^\star$ 適合 per-tensor quant 了, 但我們只是把這困難 pass 到 $b^{\star(2)}$, 為啥這麼說呢? 因為 $b^{\star(2)}$ 需要多加一項 $\hat{W}^{(2)}c$, 但我們並不做任何保證 ,因此 activations $z$ (看式 (8))仍然有可能每個 channel 維度分佈位置也都不同, 所以實務上採取 layer 1 and 2 做完, 再做 layer 2 and 3, 依此列推下去.
Bias Correction (BC)
如同在 motivation 稍微提到的, 令 $\epsilon=\tilde{W}-W$ 是 quantization error, $\tilde{W}$ 是 quant 後的參數. 且令 $y=Wx,\tilde{y}=\tilde{W}x$, 分別是 quant 前後的 output activations, 則我們有 $\tilde{y}=y+\epsilon x$.
由於 quantization 後可能 activations 的分布 mean 值不會跟原來一樣, i.e. 可能會 $\mathbb{E}[\epsilon x]\neq0$, 但可以透過下式被矯正回來: $\mathbb{E}[y]=\mathbb{E}[\tilde{y}]-\epsilon\mathbb{E}[x]$
所以只需要對 quant 完的 output 加上 $-\epsilon\mathbb{E}[x]$, 但實務上不會這麼做, 而是做在 bias parameter 裡 (bias 加上 $-\epsilon\mathbb{E}[x]$).
不過我們怎麼會知道 input activation 的期望值, $\mathbb{E}[x]$?
做完上述 CLE + bias absorption 並得到量化 model 後跟原本 float model 比較可以得到 $\epsilon$, 如果有 representative data (可以是 unlabeled) 情況下, 則丟 data 去計算 $\mathbb{E}[x]$ 就可以了. 注意要按照 layer 做, 也就是做 $l^{th}$ layer 的 BC 項時, 假設 $1, 2,..,l-1$ layer 的 BC 項都 apply 上去了. 這叫做 Empirical Bias Correction, 詳見論文 Appendix D.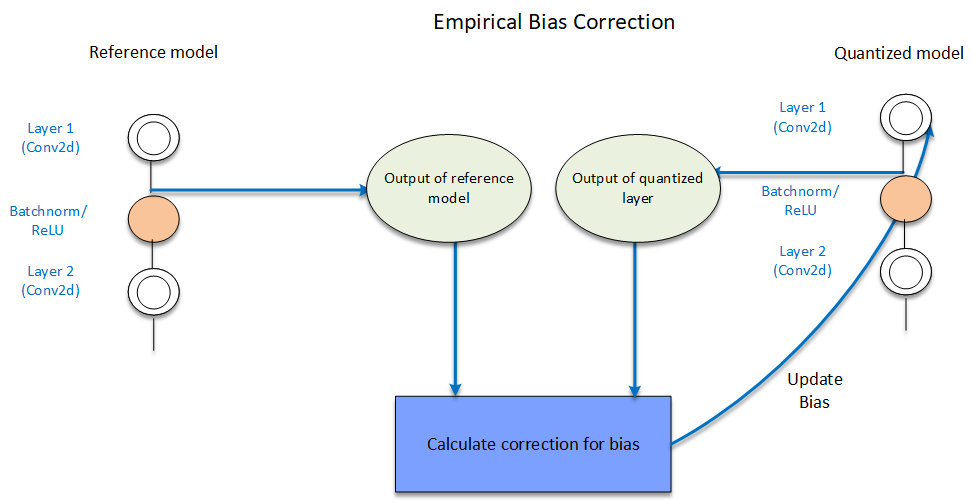
(圖來源為 AIMET Post-Training Quantization Techniques)
但論文標題是 “Data-free”, 怎麼辦呢? 此時論文要求要有這樣的 blocks 關聯:
已知目前要處理的 layer 是 $\tilde{y}=\tilde{W}x$. 論文假設此 layer 之前還有 BN and ReLU 兩個 blocks. 注意到需有這樣的關聯存在才可以.
而 $\mathbb{E}[x]$ 可以利用 BN 後 $x^{pre}$ 是 normal distribution 的特性來算. 注意到經過 ReLU 後的 $x$ 變成 clipped normal distribution, 而其 mean 可以利用 BN 的 shift and scale parameters 寫出 closed form 解.
詳細直接參考論文, Appendix C 有推導. 這樣的做法稱 Analytical Bias Correction.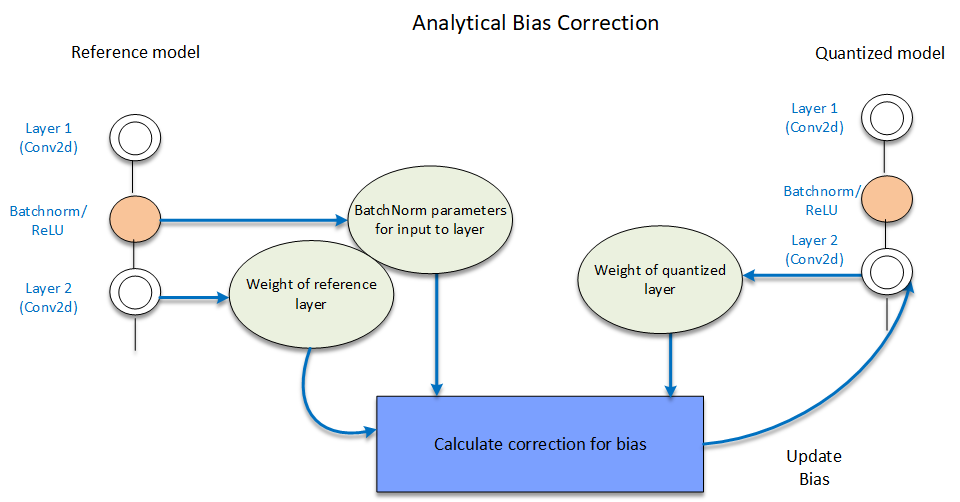
(圖來源為 AIMET Post-Training Quantization Techniques)
Experiments
由於 CLE and BA 目的是讓後面的 quantization 比較適合 per-tensor, 所以要觀察以下兩點:
1. 用了 CLE and/or BA 後, 由於輸出還是 float model, 那跟用之前的 float model 有無 performance 影響?
2. 用了 CLE and/or BA 後, 再用了 per-tensor 量化後, 能否逼近原本 float model (沒用 CLE/BA) 的 per-channel 量化?
結果 Table 1 顯示以上兩點都沒問題.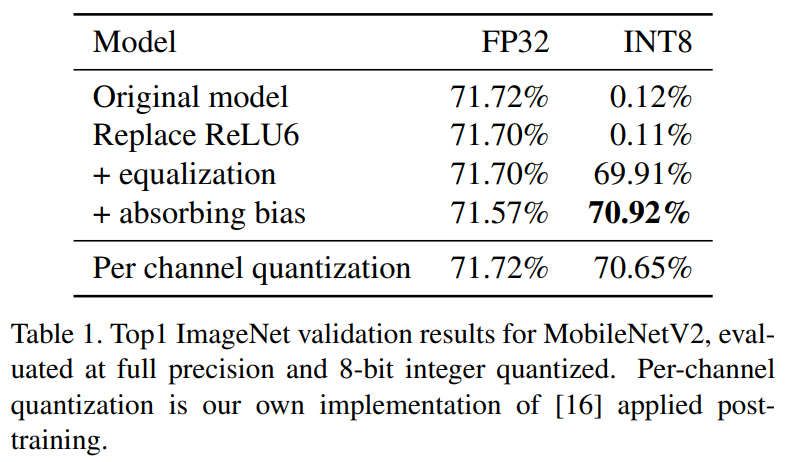
再來如果加入 BC 則觀察能否補償因 quantization 造成的 mean 偏移損失? 其中可以看 quantization model 有無套用 CLE+BA.
結果如 Table 2: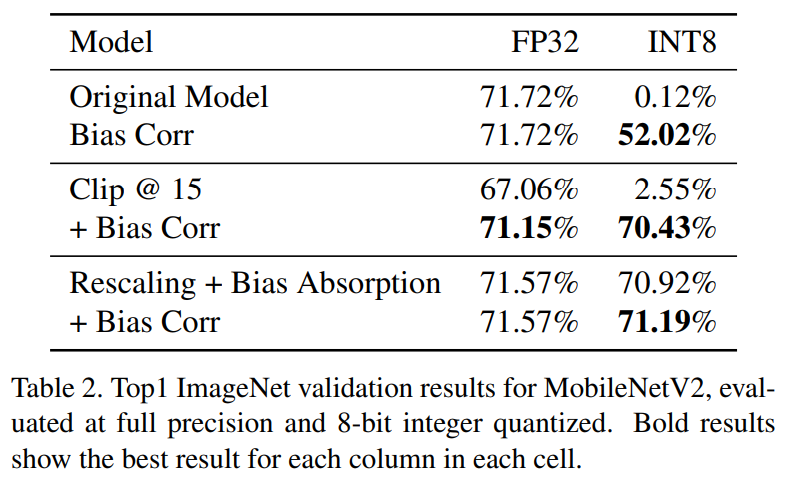
Original model 直接硬做 PTQ to INT8 是慘不忍睹的 random 行為, 但直接加上 BC 補償後竟然就回到 52.02%!
如果先用 CLE+BA 在量化到 INT8, performance 為 Table 1 的最佳 70.92%. 這種情況再加上 BC 還能提升一點點 (多少表示可能還是存在一點點的 mean 偏移)
Clip@15 這個方法是直接對 weights 砍到 [-15, 15] 區間, 跟 CLE 目的一樣只是直接粗暴, 當然 BC 就能發揮更好的作用 (2.55% —> 70.43%).
剩下的實驗就不細說.
AIMET Quantization Flow
以下為 AIMET AutoQuant 建議的量化流程, 總結得很不錯: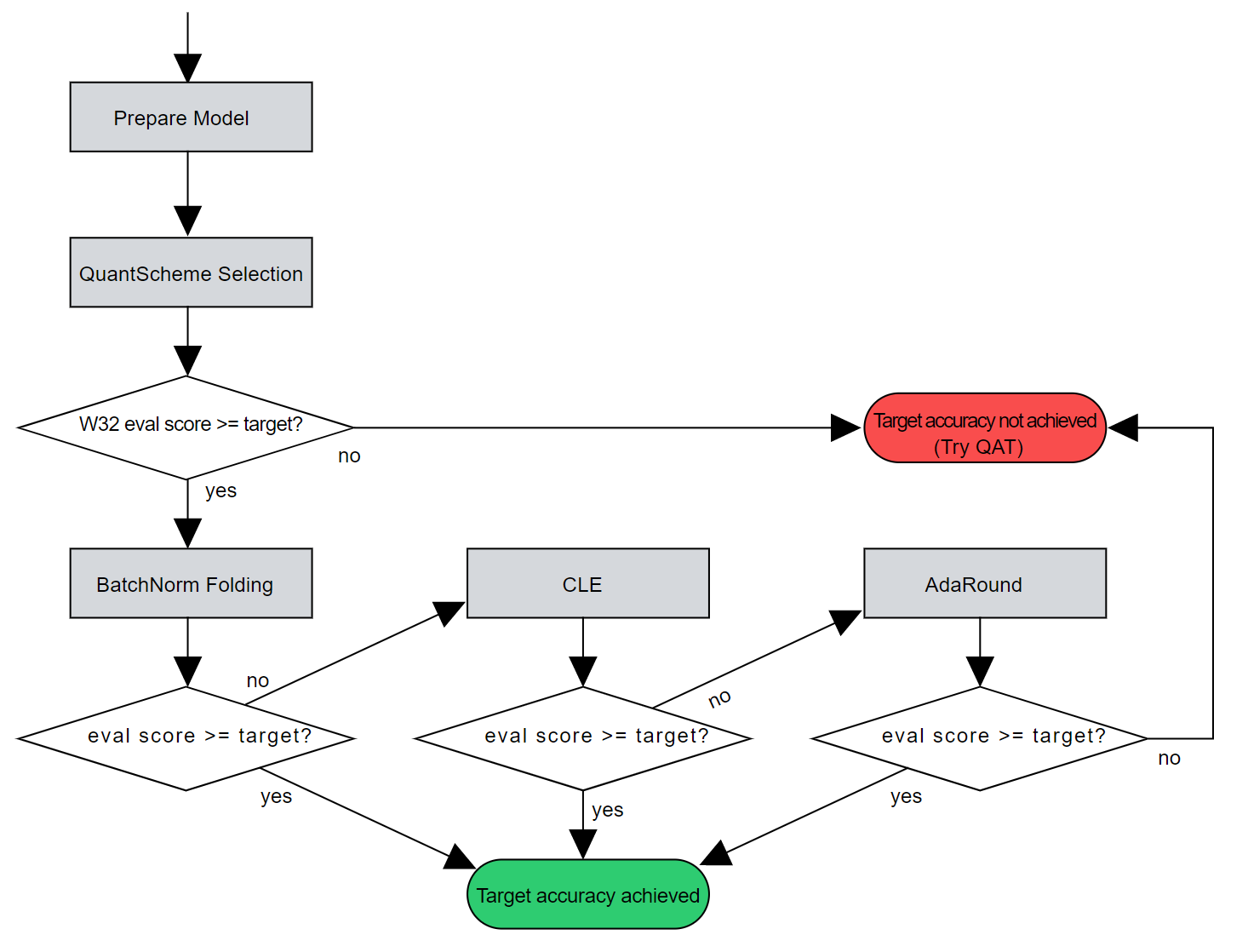
圖中的 CLE 我猜已經包含 BA 了, 然後可以看到沒有 BC, 因為被 AdaRound 取代掉
也注意到在給 CLE 之前要先做 BatchNorm folding (如同我們在講 CLE 的限制 2)
流程就是建議先對 floating model 插好 fake quant op 來模擬 target HW 的 operators 行為 (QuantScheme Selection 那步). 先看看效果如何, 如果 OK 那 PTQ/QAT 都不需要.
接著才確認 BN folding 是否能幫助提升效果? 不行的話套看看 PTQ 的 CLE (w/wo AdaRound). 再不行就要走 QAT 了.
到這終於紀錄完, 這篇初看感覺應該可以很快看完, 一讀才發現細節真的有夠多, 頗不容易. 也因為很認真細讀才發現其實有不少限制. 不過還是很有收穫拉~
總之恭喜讀者(自己?)有耐心看完(寫完). ~~ 撒花收工 ~~
Appendix 證明 CLE 的最佳解
Render 爛掉了, 直接怒貼圖…
