⚠️ 可能寫的比較瑣碎和雜亂, 主要給自己筆記用
令 $f:\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$ 的 Jacobian matrix 為 $J_f(x)$ 是 $(m\times n)$ 矩陣, 而 Hessian 為 $H_f(x)$ 是 $(m\times n \times n)$ 高維 tensor
$\circ$ VJP 稱為 Vector-Jacobian Product, $vJ_f(x)$, 其中 $v$ 是 ($1\times m$) 的 row vector
$\circ$ JVP 稱為 Jacobian-Vector Product, $J_f(x)v$, 其中 $v$ 是 ($n\times 1$) 的 column vector
$\circ$ HVP 稱為 Hessian-Vector Product, $H_f(x)v$, 其中 $v$ 是 ($n\times 1$) 的 column vector
計算 $vJ_f(x)$ 不用先把矩陣 $J_f(x)$ 求出來再跟 $v$ 相乘, 而是可以直接得到相乘的結果(這樣做還更快), 聽起來有點矛盾對吧~同樣的 JVP 和 HVP 也是如此
本文會說明怎麼高效率計算 VJP, JVP, Jacobian, Hessian, 以及 HVP
主要參考 PyTorch 文章: JACOBIANS, HESSIANS, HVP, VHP, AND MORE: COMPOSING FUNCTION TRANSFORMS
HVP 可以用來有效率地計算 $tr(H_f(x))$, 而這個 term 有時候會被當作 loss 來用, 舉例來說:
$\circ$ Sliced Score Matching (SSM) 會用到
$\circ$ EWGS quantization (Network Quantization with Element-wise Gradient Scaling, arxiv) 會用到
$\circ$ More and details see: Thoughts on Trace Estimation in Deep Learning, 更多例子且有非常深入的討論
總結可以參考文末 Summary
先把 function $f$ 定義好: (名字為predict)
Vector-Jacobian Products (VJPs)
$f:\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$, $y=f(x)$, VJP 基本就是 $vJ_f(x)$.
計算上就是一個 row vector ($1\times m$) 乘上 Jacobian matrix, $J_f(x)=\partial y/\partial x:m\times n$ 矩陣, 我們這麼寫:
PyTorch function
torch.func.vjp(func,*primals,...)的primals指的是 $x$, 會 return 一個 function 例如稱 $g$, 則 $g(v)=vJ_f(x)$.
這樣看起來要計算 $vJ_f(x)$ 還是要先把 $J_f(x)$ 這個 $m\times n$ 矩陣先算出來再跟 $v$ 相乘. 但其實不用, 我們可以直接算結果, i.e. 省去顯式地先算 $J_f(x)$, 而這樣做會更有效率!
怎麼做到呢? 我們可以這麼改寫:
$$vJ_f(x)=v\frac{\partial f(x)}{\partial x}=\frac{\partial (vf(x))}{\partial x}$$ $v$ 是一個 ($1\times m$) 的 row vector, $f(x)$ 是一個 ($m\times 1$) column vector. $J_f(x)=\partial f(x)/\partial x:m\times n$ 矩陣.
這樣改寫的好處是 $vf(x)$ 已經是一個 scalar 了, 現在改成對 scalar 做 gradient 就可以得到答案, 並且是很有效率的, 所以不用先算出 $J_f(x)$ 這個 $m\times n$ Jacobian 矩陣.
對照一下 PyTorch 的 torch.autograd.grad
grad_outputs 其實就是上面的 $v$. 以 chainrule 來看,
$${\partial L \over \partial x} = {\partial L \over \partial y} \cdot {\partial y \over \partial x}=v\cdot J_f(x)$$ 因為 PyTorch 的 loss 一定是 $L:\mathbb{R}^m\rightarrow\mathbb{R}$, 所以 $\partial L / \partial y: (1\times m)$ 的 row vector, 以 VJP 的型式來看就是是指 $v$.
或說利用 grad 計算 $\partial L/\partial x$ 的時候 grad_outputs 給的就是 $\partial L / \partial y: (1\times m)$.
求 Jacobian Matrix
PyTorch 介紹3種求 Jacobian 的方式:
1. For-loop 求 Jacobian
2. 用 vmap-vjp 求 Jacobian
3. 用 jacrev 求 Jacobian
1. For-loop 求 Jacobian
如果 $v=e_i$, 則 $vJ_f(x)$ 為 i-th row of $J_f(x)$. 因此只要把 $i=1,…,m$ 都執行一次, 則能得到完整的 $J_f(x)$.
2. 用 vmap-vjp 求 Jacobian
但想像上每一個 row 的計算可以並行, 因此使用 vjp and vmap 來並行計算.
vjp就是算一次 $vJ_f(x)$, 但這是一筆 sample, 如果要對一個 batch $V^T=[v_1^T,…,v_N^T]$ 計算 $VJ_f(x)$, 就套用vmap在vjp上, 讓他並行 vectorized 算.
解說一下 vmap, 以這個範例來說會回傳 vmap_vjp_fn 這個 function, 其 input argument 會跟 vjp_fn 一樣.
差別是 vmap_vjp_fn 的 input argument unit_vectors 會比 vjp_fn 的 input argument x 多了一個 batch 的維度 (預設在維度0)
即 x 是維度 (n, ), unit_vectors 是維度 (m, n) 這裡的 m 是 batch 維度.
3. 用 jacrev 求 Jacobian
或直接使用 jacrev 直接幫忙做好 vmap-vjp 兩步驟
torch.func.jacrev(func,argnums=0,...)的說明:
Returns a function that takes in the same inputs asfuncand returns the Jacobian offuncwith respect to the arg(s) atargnums
當然我們也可以針對 weight or bias 計算 Jacobian, 只需要對 argnums 改成 0 or 1 即可
Jacobian-Vector Products (JVPs)
$f:\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$, $y=f(x)$, JVP 基本就是 $J_f(x)v$, 計算上就是 Jacobian matrix, $J_f(x)=\partial y/\partial x:m\times n$, 乘上一個 column vector ($n\times 1$) 我們這麼寫: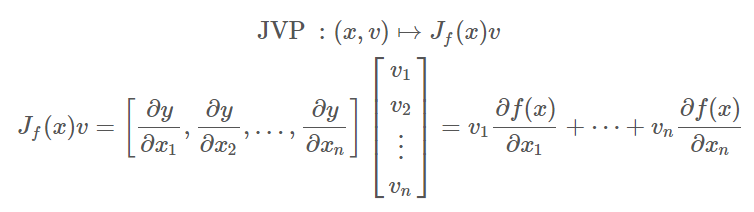
PyTorch function
torch.func.jvp(func, primals, tangents, ...)的primals指的是 $x$,tangents指的是 $v$.
同樣的如果 $v=e_i$, 則 $J_f(x)v$ 為 i-th column of $J_f(x)$. 所以對於計算 Jacobian matrix:
$\circ$ VJP 有 jacrev (稱 reverse-mode Jacobian)
$\circ$ JVP 有 jacfwd (稱 forward-mode Jacobian)
VJP and JVP 速度上的考量
Let $f:\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$, VJP 使用 vmap 在 output 維度 $m$ 上, 反之 JVP 使用 vmap 在 input 維度 $n$ 上.
使用 vmap 的那個維度如果比較大的話, 效率可能會比較差, 因此建議 vmap 作用在小的維度上.
因此如果 Jacobian 是瘦高矩陣 $m>n$ 建議使用 JVP jacfwd, 反之胖矮矩陣 $n>m$ 建議使用 VJP jacrev.
Hessian 計算
使用 torch.func.hessian 可以幫忙計算出 Hessian matrix.
我們知道 Hessian matrix 是二次微分, 因此可以套用算 Jacobian 的 Jacobian matrix 得到.
所以實際上底層運作為 hessian(f)=jacfwd(jacrev(f)).
也可以使用
jacfwd(jacfwd(f))或jacrev(jacrev(f))根據矩陣寬高維度來增加效率.
計算 Batch Jacobian and Batch Hessian
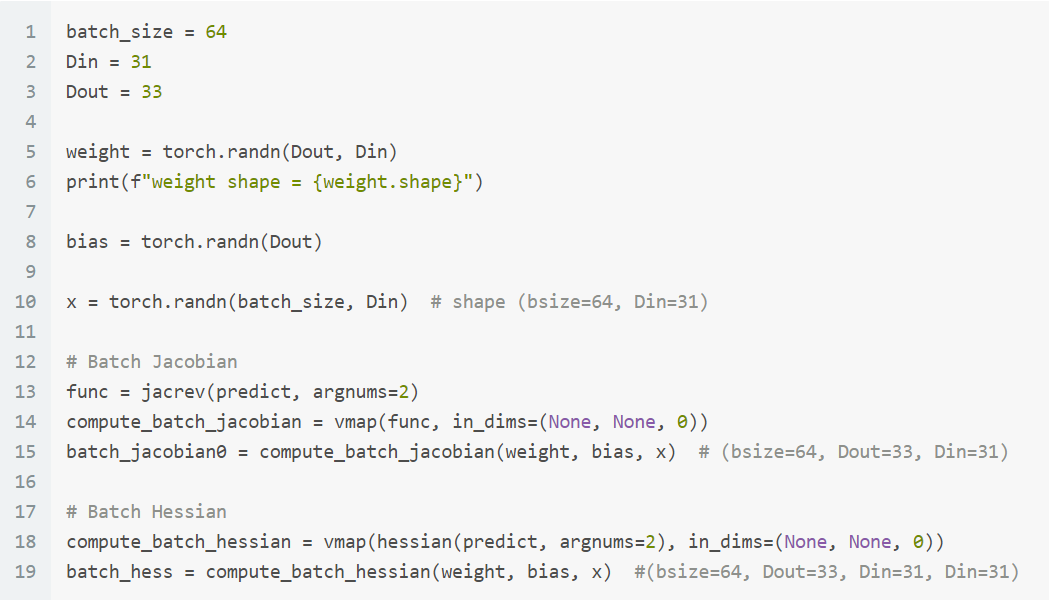說明一下 func = jacrev(predict, argnums=2) 和 vmap(func, in_dims) 這兩行:jacrev(predict, argnums=2) 會回傳一個 function 稱 func, 這個 func 的 input arguments 會跟 predict 一樣, 也就是 (weight, bias, x)
然後 argnums=2 表示偏微分的變數為 index 2 即 x.
執行 func 會 return Jacobian matrix, 即為一個 shape (Dout, Din) 的矩陣.
然後 vmap 的 in_dims=(None, None, 0) 表示 func 的這3個 input arguments 要對哪一個 argument 的哪一個維度 index 當作執行 vectorized 並行運算. 這裡的例子是對第3個 argument 的 index 0, 即 argument x 的 batch_size 那一維度. 而 vmap 也是 return 一個 function 叫 compute_batch_jacobian 只是 output 會比原本的 func 回傳結果多了一個 batch 的維度.
另外可以使用 sum trick 來避掉使用 vmap 這有點 tricky
注意到這個 function predict_with_output_summed 是 $\mathbb{R}^b\times \mathbb{R}^n\rightarrow\mathbb{R}^{m}$ 所以這個 function 的 Jacobian matrix 維度是 $(m, (b, n))$, 實際上是 $(m, b, n)$ 這個正是 jacrev return 的 shape, 然後再 movedim 變成 $(b, m, n)$.
計算 Hessian-Vector Products (HVP)
$$y=H_L(x)v$$ 其中 $x\in\mathbb{R}^n$, $L:\mathbb{R}^n\rightarrow \mathbb{R}$, $H(x)=\partial^2L/(\partial x)^2:\mathbb{R}^n\rightarrow \mathbb{R}^n$, $v:\mathbb{R}^n$.
如同我們在 VJP, $vJ_f(x)$, 提到不用先算出 $J_f(x)$ 這個 $m\times n$ Jacobian 矩陣, 因此 VJP 可以很有效率計算. HVP 也一樣, 不用先算出 $H_L(x)$, 可以直接有效率地算出 $H_L(x)v$:
$$H_L(x)v=\frac{\partial G_L^T(x)}{\partial x}v=\frac{\partial G_L(x)^Tv}{\partial x}$$ 其中 $G_L(x)$ 是 gradient, 為 $n\times 1$ 的 column vector. 這樣做的好處是 $G_L(x)^Tv$ 已經是一個 scalar 了, 做偏微分很有效率, 也避開要算 $H_L(x)$.
用 jvp 和 grad 來完成 HVP, primals 指的是 $x$, tangents 指的是 $v$.
注意到 grad [link] (注意這裡說的是 torch.func.grad 不是 torch.autograd.grad 喔) 的 function 只能接受 output dimension 是 $\mathbb{R}$ (f 只能 return scalar), 而 jacrev or jacfwd 可以處理 function 的 output 是 $\mathbb{R}^m$.
雖然都是算一次微分但有這個不同要注意!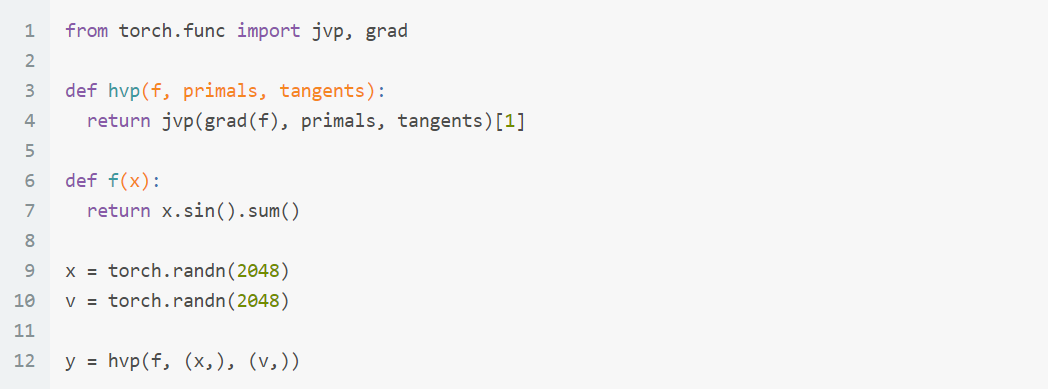
PyTorch 文件說使用 jvp 這種 forward-mode AD 不用建立 Autograd graph 所以會比較省 memory
Benchmarking HVP
我們對比兩個方法:
1. Baseline: 先計算出 $H_L(x)$, 再和 $v$ 相乘
2. 上面的 hvp 高效率計算方式
簡單實驗得到 hvp 所花的時間為 Baseline 的 84.4477%, 加速很有效! (不同機器可能會不同)
這個 hvp 雖然有效率, 但有點麻煩是因為使用 torch.func.grad 這個 function 它的 input f (也就是上面範例的 predict) 必須 return scalar.
而實際上我們都會是多維的結果, 至少會有一個 batch size 維度.
考量到這種用法, 我想直接參考 Sliced score matching 的 toy example codes 這段, 可能這麼寫就好. 注意到裡面的 score 已經是 gradient 了, 請讀者再讀一下 codes 可以發現確實跟上述 hvp 的做法一樣.
Summary
令 $f:\mathbb{R}^{n}\rightarrow\mathbb{R}^{m}$ 的 Jacobian matrix 為 $J_f(x)$ with shape $(m, n)$, 而 Hessian 為 $H_f(x)$ with shape $(m,n,n)$
$\circ$ VJP: torch.func.vjp 可以有效率的來計算 $vJ_f(x)$, 不用真的把 $J_f(x)$ 先算出來, 就可以直接計算 vjp 的結果.
$\circ$ JVP: torch.func.jvp 可以有效率的來計算 $J_f(x)v$, 不用真的把 $J_f(x)$ 先算出來, 就可以直接計算 jvp 的結果.
$\circ$ Vectorized: 可利用 vmap 來做到 batch processing
$\circ$ Jacobian: torch.func.jacrev 和 torch.func.jacfwd 可以有效率求出 $J_f(x)$: 用 vmap + jvp or vjp
$\circ$ Hessian: torch.func.hessian=jacfwd(jacrev(f)) 可以有效率求出 $H_f(x)$
$\circ$ HVP: 可以利用 jvp and grad 來有效率計算出 hvp: $H_f(x)v$, 不用真的把 Hessian matrix $H_f(x)$ 先算出來, 就可以直接計算 hvp 的結果.