訓練模型時我們盯著 tensorboard 看著 training loss 一直降低直到收斂, 收斂後每個 checkpoint 的 training loss 都差不多, 那該挑哪一個 checkpoint 呢?
就選 validation loss 最低的那些吧, 由 PAC 我們知道 validation error 約等於 test error (validation set 愈大愈好), 但我們能不能對泛化能力做得更好? 如果 training 時就能讓泛化能力提升, 是否更有效率?
Motivation
很多提升泛化能力的論文和觀點都從 “flat“ optimum 出發. 下圖清楚說明這個想法 ([圖來源]):
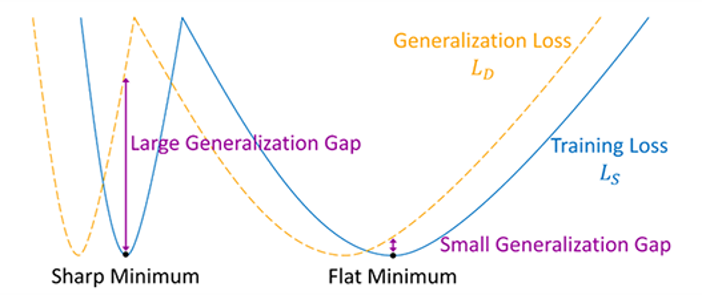Flat 比起 sharp optimum 更 robust 我想就不多描述.
上篇提到的 SAM 藉由定義什麼是 sharpness loss:
$$\begin{align}
L_\text{sharpness}(\theta)\triangleq\left[
\max_{\|\varepsilon\|_p\leq\rho} L(\theta+\varepsilon)
\right] - L(\theta)
\end{align}$$ 來幫助找到的 optimum 是夠 flat 的. Sharpness loss 定義了 “附近” ($\rho$ 距離內) Loss 的最大變化量. 直覺上 loss 變化愈大則愈 sharp.
因此 SAM loss 就是 sharpness loss 加上原來的 training loss 加上 regularization term (原始論文從 PAC 推導而得):
$$\begin{align}
L_\text{SAM}(\theta) \triangleq L_\text{sharpness}(\theta) + L(\theta) + \lambda\|\theta\|_2^2 \\
= \max_{\|\varepsilon\|_p\leq\rho} L(\theta+\varepsilon) + \lambda\|\theta\|_2^2
\end{align}$$ 得到第 t 次 iteration 的 gradient 有如下的高效近似解:
$$\begin{align}
\nabla L_\text{SAM}(\theta_t) \approx \nabla L(\theta'_t) \\
\text{where}\quad \theta'_t=\theta_t+\rho\cdot\frac{\nabla L(\theta_t)}{\|\nabla L(\theta_t)\|_2}
\end{align}$$ 意思是做 SGD 時原來的 gradient ($\nabla L(\theta_t)$) 用在 $\theta’_t$ 這個位置計算的 gradient 取代
這篇論文把 gradient norm 當作 penalty 加到 training loss 後:
$$\begin{align}
L'(\theta) = L(\theta) + \lambda\cdot\|\nabla L(\theta)\|_2
\end{align}$$ 推導出來其實 SAM 的做法是個特例 ($\alpha=1$), gradient update 應為:
$$\begin{align}
\nabla L'(\theta_t) \approx (1-\alpha)\nabla L(\theta_t) + \alpha\nabla L(\theta'_t) \\
\text{where}\quad \theta'_t=\theta_t+\rho\cdot\frac{\nabla L(\theta_t)}{\|\nabla L(\theta_t)\|_2},\quad\alpha=\lambda/\rho
\end{align}$$ 所以或許要與原來位置的 gradient ($\nabla L(\theta_t)$) 做 linear combination 會比較好.
所以我們的問題變成, gradient norm 怎麼跟 flatness optimum 關聯起來? (透過 Lipschitz Continuous) 以下筆記下該論文: [Penalizing Gradient Norm for Efficiently Improving Generalization in Deep Learning], 並順便討論下之前讀的有關 flat optimum 的其他論文關聯.
Lipschitz Continuous 與 Flatness 和 Gradient Norm 的關聯
予 $\Omega\subset\mathbb{R}^n$, function $h:\Omega\rightarrow\mathbb{R}^m$ 稱 Lipschitz continuous 如果存在 $K>0$ s.t. $\forall\theta_1,\theta_2\in\Omega$ 滿足
$$\begin{align}
\|h(\theta_1)-h(\theta_2)\|_2 \leq K\cdot\|\theta_1-\theta_2\|_2
\end{align}$$ Lipschitz constant 指的是那個最小的 $K$.
直覺上 Lipschitz continuous 限制了 output change. 所以如果在一個 neighborhood $A$ 中, $h|_A$ 是 Lipschitz continuous, 我們可以想成在 $A$ 這個範圍中 $h$ 看起來都很 smooth ($K$ 愈小愈 smooth)
因此我們把 Lipschitz continuous 跟 flatness 可以聯繫起來, 那跟 gradient norm 呢?
給一個 local minimum $\theta_\ast\in A$, 根據 mean value theorem 得 $\forall \theta'\in A$, $\exists 0\leq t\leq1,\zeta:=t\theta'+(1-t)\theta_\ast\in A$, 我們有
$$\begin{align}
\|h(\theta')-h(\theta_\ast)\|_2 = \|\nabla h(\zeta)\cdot(\theta'-\theta_\ast)\|_2 \\
\leq \|\nabla h(\zeta)\|_2\cdot\|\theta'-\theta_\ast\|_2
\end{align}$$ 想像一下如果 $\theta’$ 愈接近 $\theta_\ast$, 則 $\|\nabla h(\zeta)\|_2$ 會愈接近 locally 的 Lipschitz constant.
因此 gradient norm 也跟 flatness 聯繫起來了.
“Locally” 來看, gradient norm 跟 Lipschitz constant 很接近. 而愈小的 Lipschitz constant 表示愈 flat. 因此愈小的 gradient norm 相當於愈 flat.
使用 Gradient Norm 當 Penalty
最直覺的就是加到原來的 training loss 裡面 (式 (6)) 然後一起訓練. 要把 gradient 也當 loss 的一部分需要用到 torch.autograd.grad 並把參數 retain_graph 和 create_graph 設定成 True, 這相當於把計算 gradient 也加入到 forward graph 中, 因此就能計算二次微分. 這麼做其實很沒有效率也很吃 memory. 因此論文做了一些推導求高效的近似解.
對式 (6) 計算 gradient:
$$\begin{align} \nabla L'(\theta)=\nabla L(\theta) + \nabla(\lambda\cdot\|\nabla L(\theta)\|_2) \end{align}$$ 根據 chain rule (參見文末的 Aappendix)
$$\begin{align} \nabla L'(\theta)=\nabla L(\theta) + \lambda\cdot\nabla^2 L(\theta)\frac{\nabla L(\theta)}{\|\nabla L(\theta)\|} \end{align}$$ 令 $H:=\nabla^2 L(\theta)$ and $v:={\nabla L(\theta)}/{\|\nabla L(\theta\|}$, 替換一下變數變成
$$\begin{align} \nabla L'(\theta)=\nabla L(\theta) + \lambda\cdot Hv \end{align}$$ 由於算 Hessian matrix $H$ 代價很大, 要繼續簡化, 使用泰勒展開式先觀察:
$\nabla L(\theta+\Delta\theta)=\nabla L(\theta) + H\Delta\theta + O(\|\Delta\theta\|^2)$ 令 $\Delta\theta:=r\cdot v$ 代入得到
$$\nabla L(\theta+r\cdot v)=\nabla L(\theta) + r\cdot Hv + O(r^2) \\ \Longrightarrow Hv\approx \left[{\nabla L\left(\theta+r\cdot\frac{\nabla L(\theta)}{\|\nabla L(\theta)\|}\right) - \nabla L(\theta)} \right]/ {r}$$ 所以代入到 (14) 得到
$$\begin{align} \nabla L'(\theta) \approx \nabla L(\theta) + \frac{\lambda}{r}\cdot \left[{\nabla L\left(\theta+r\cdot\frac{\nabla L(\theta)}{\|\nabla L(\theta)\|}\right) - \nabla L(\theta)} \right] \\ =(1-\alpha)\nabla L(\theta) + \alpha\nabla L\left(\theta+r\cdot\frac{\nabla L(\theta)}{\|\nabla L(\theta)\|}\right) \\ =(1-\alpha)\nabla L(\theta) + \alpha \nabla L(\theta') \end{align}$$ 令 $\theta':=\theta+r\cdot {\nabla L(\theta)}/{\|\nabla L(\theta)\|}$, where $\alpha=\lambda/r$ 稱 balance coefficient. 即推導出式 (7) and (8) 的 gradient update.
論文實驗如下圖, 顯示 $\alpha$ 約在 0.6~0.8 是最佳的, 比 $\alpha=1$ 的 SAM case 更好
圖中的 r 是 $\rho$ 定義了所謂的 “附近”, 愈小理論上上面推導的近似會愈精確 (因為 Talyor expansion 愈精確) 但比較會有數值問題.
其他討論
其實我們在用的 SGD 已經多少隱含了加入 gradient norm 當 penalty term 了, 所以隱含了找 flat optimum. 參見之前的筆記 [SGD 泛化能力的筆記], 只是 SAM 和 Gradient norm penalty 顯示地找 flat optimum 而已. 但要注意的是 SAM or Gradient norm penalty 的做法每一次的 iteration 會多一次的 forward-backward 計算, 因此訓練時間可能會更久.
另外還有一些變形, 例如 Adaptive SAM (ASAM), Gap Guided Sharpness-Aware Minimization (GSAM), Sparse SAM (SSAM) 等. 有興趣可以繼續往這 topic 研究下去.
另外 Stochastic Weight Averaging (SWA) [之前的筆記] 這樣簡單的做法也宣稱找到的 optimum 比較 flat.
Anyway, flat optimum 比較 robust, 而加入 gradient norm 有助於我們找 flat optimum, 且有一個高效的近似作法 (7) and (8)
Appendix
(12) to (13) 的推導只要把握 norm 的微分和 chain rule 即可 (論文 Appendix 照抄而已):
$\theta=[\theta_1, \theta_2, ..., \theta_n]^T$, 2-norm 命為 $g$
$$g(\theta):=\|\theta\|_2=\sqrt{\theta_1^2+\theta_2^2+...+\theta_n^2}$$ 則微分為
$$\frac{\partial g(\theta)}{\partial \theta_i}=\frac{\theta_i}{\sqrt{\theta_1^2+\theta_2^2+...+\theta_n^2}}=\frac{\theta_i}{\|\theta\|_2}=\frac{\theta_i}{g(\theta)}$$ 所以
$$\nabla g(\theta)=\left[\frac{\theta_1}{g(\theta)}, \frac{\theta_2}{g(\theta)}, ..., \frac{\theta_n}{g(\theta)}\right]^T$$ 讓 $h(\theta):=\nabla L(\theta)$, 則 $\nabla(\|\nabla L(\theta)\|_2)$ 可寫成 $\nabla( g\circ h) (\theta)$ 所以
$$\nabla (\|\nabla L(\theta)\|_2)=\nabla( g\circ h) (\theta) \\ =\nabla g(\zeta)|_{\zeta=h(\theta)}\cdot \nabla h(\theta) \\ =\left(\left.\frac{\zeta}{g(\zeta)}\right|_{\zeta=h(\theta)}\right)\cdot \nabla^2 L(\theta) \\ = \frac{\nabla L(\theta)}{\|\nabla L(\theta)\|_2} \cdot \nabla^2 L(\theta)$$ 代回去 (12) 即可得到 (13)
References
- Sharpness-Aware Minimization for Efficiently Improving Generalization [arxiv]
- Penalizing Gradient Norm for Efficiently Improving Generalization in Deep Learning [arxiv]
- ASAM: Adaptive Sharpness-Aware Minimization for Scale-Invariant Learning of Deep Neural Networks [arxiv], [SAMSUNG Research blog]
- Surrogate Gap Minimization Improves Sharpness-Aware Training (GSAM) [arxiv]
- Make Sharpness-Aware Minimization Stronger: A Sparsified Perturbation Approach (SSAM) [arxiv]
- Why Stochastic Weight Averaging? averaging results V.S. averaging weights [blog]
- SGD 泛化能力的筆記 [blog]